1671 г машина лейбница могла умножать и делить
Калькулятор Лейбница
Первая счетная машина, позволявшая производить умножение и деление также легко, как сложение и вычитание, была изобретена в Германии в 1673 году Готфридом Вильгельмом Лейбницем (1646-1716), и называлась «Калькулятор Лейбница».
Идея создать такую машину у Вильгельма Лейбница появилась после знакомства с голландским астрономом и математиком Христианом Гюйгенсом. Видя нескончаемые вычисления, которые астроному приходилось производить, обрабатывая свои наблюдения, Лейбниц решил создать устройство, которое ускорило и облегчило бы эту работу.
Первое описание своей машины Лейбниц сделал в 1670 году. Через два года ученый составил новое эскизное описание, на основе которого в 1673 году построил действующее арифметическое устройство и продемонстрировал его в феврале 1673 года на заседании Лондонского Королевского общества. В заключение своего выступления он признал, что устройство не совершенно, и пообещал его улучшить.
В 1674 – 1676 годах Лейбниц провел большую работу по улучшению изобретения и привез в Лондон новый вариант калькулятора. Это была малоразрядная модель счетной машины, не пригодная для практического применения. И только в 1694 году Лейбниц сконструировал 12 разрядную модель. Впоследствии калькулятор несколько раз дорабатывался. Последний вариант был создан в 1710 году. По образцу двенадцатиразрядной счетной машины Лейбница в 1708 году профессор Вагнер и мастер Левин создали шестнадцатиразрядную счетную машину.
Как видно, работа над изобретением была длительной, но не непрерывной. Лейбниц одновременно трудился в самых разных областях науки. В 1695 году он писал: «Уже свыше двадцати лет назад французы и англичане видели мою счетную машину. с тех пор Ольденбург, Гюйгенс и Арно, сами или через своих друзей, побуждали меня издать описание этого искусного устройства, а я все откладывал это, потому что я сперва имел только маленькую модель этой машины, которая годится для демонстрации механику, но не для пользования. Теперь же с помощью собранных мною рабочих готова машина, позволяющая перемножать до двенадцати разрядов. Уже год, как я этого достиг, но рабочие еще при мне, чтобы можно было изготовить другие подобные машины, так как их требуют из разных мест».
Работа над калькулятором Лейбницу обошлась в 24 000 талеров. Для сравнения, годовая зарплата министра по тем временам составляла 1 – 2 тысячи талеров.
К сожалению, с полной уверенностью не об одной из сохранившихся моделей калькулятора Лейбница нельзя сказать, что она была создана именно автором. Из-за чего существует много предположений относительно изобретения Лейбница. Есть мнения, что ученый только высказал идею применения ступенчатого валика, или что он не создавал калькулятор целиком, а только демонстрировал работу отдельных механизмов устройства. Но, несмотря на все сомнения, можно точно утверждать, что идеи Лейбница надолго определили путь развития вычислительной техники.
Мы будем вести описание калькулятора Лейбница на основе одной из сохранившихся моделей, находящейся в музее в Ганновере. Она представляет собой ящик около метра длинной, 30 сантиметров шириной и около 25 сантиметров высотой.
Изначально, Лейбниц пытался лишь улучшить уже существующее устройство Паскаля, но вскоре он понял, что операция умножения и деления требуют принципиально нового решения, которое бы позволяло вводить множимое только один раз.
О своей машине Лейбниц писал: «Мне посчастливилось построить такую арифметическую машину, которая бесконечно отличается от машины Паскаля, так как моя машина дает возможность совершать умножение и деление над огромными числами мгновенно, притом не прибегая к последовательному сложению и вычитанию».
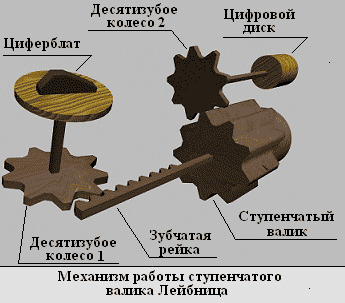
Это стало возможно, благодаря разработанному Лейбницем цилиндру, на боковой поверхности которого, параллельно образующей, располагались зубья различной длины. Этот цилиндр получил название «Ступенчатый валик».
К ступенчатому валику крепится зубчатая рейка. Эта рейка входит в сцепление с десятизубым колесом №1, к которому прикреплялся циферблат с цифрами от 0 до 10. Поворотом этого циферблата задается значение соответствующего разряда множимого.
Например, если второй разряд множимого равнялся 5, то циферблат, отвечающий за установку этого разряда, поворачивался в положение 5. В результате десятизубое колесо № 1, с помощью зубчатой рейки, так перемещало ступенчатый валик, что при повороте на 360 градусов он входит в зацеплении с десятизубым колесом № 2 только пятью наиболее длинными ребрами. Соответственно, десятизубое колесо №2 поворачивалось на пять частей полного оборота, на столько же поворачивался и связанный с ним цифровой диск, отображающий результирующее значение выполненной операции.
При следующем обороте валика на цифровой диск снова перенесется пятерка. Если цифровой диск совершал полный оборот, то результат переполнения переносился на следующий разряд.
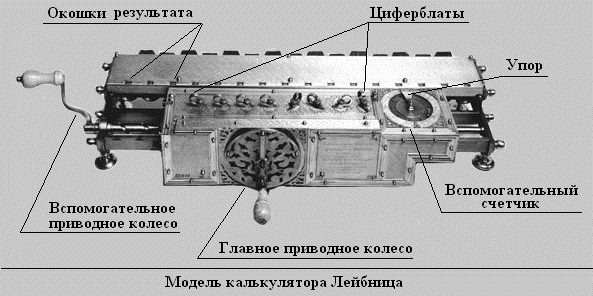
Поворот ступенчатых валиков осуществлялся с помощью специальной ручки – главного приводного колеса.
Таким образом, при выполнении операции умножения не требовалось многократно вводить множимое, а достаточно вести его один раз и повернуть ручку главного приводного колеса столько раз, на сколько необходимо произвести умножение. Однако, если множитель будет велик, то операция умножения займет длительное время. Для решения этой проблемы Лейбниц использовал сдвиг множимого, т.е. отдельно происходило умножение на единицы, десятки, сотни и так далее множителя.
Так же для облегчения умножения и деления Лейбниц разработал вспомогательный счетчик, состоящий из трех частей.
Средняя часть вспомогательного счетчика – подвижная, которая служит для отсчета количества сложений при умножении и вычитаний при делении. На ней имеется десять отверстий, напротив цифр внешней и внутренней частей счетчика, в которые вставляется штифт для ограничения вращения счетчика.
При полном повороте главного приводного колеса средняя часть вспомогательного счетчика поворачивается на одно деление. Если предварительно вставить штифт, например, в отверстие напротив цифры 4 внешней части вспомогательного счетчика, то после четырех оборотов главного приводного колеса этот штифт наткнется на неподвижный упор и остановит вращение главного приводного колеса.
Рассмотрим принцип работы калькулятора Лейбница на примере умножения 10456 на 472:
1. С помощью циферблатов вводится множимое (10456).
2. Устанавливается штифт в среднюю часть вспомогательного счетчика, напротив цифры 2, нанесенной на наружную часть вспомогательного счетчика.
3. Поворачивают главное приводное колесо по часовой стрелки, пока штифт, вставленный в вспомогательный счетчик, не упрется в упор (два поворота).
4. Сдвигается подвижная часть калькулятора Лейбница на одно деление влево, используя вспомогательное приводное колесо.
5. Устанавливается штифт в среднюю часть вспомогательного счетчика, напротив цифры, соответствующей количеству десяток множителя (7).
6. Поворачивается главное приводное колесо по часовой стрелки, пока штифт, вставленный в вспомогательный счетчик, не упрется в упор (семь поворотов).
7. Подвижная часть калькулятора Лейбница сдвигается еще на одно деление влево.
8. Устанавливается штифт в среднюю часть вспомогательного счетчика, напротив цифры, соответствующей количеству сотен множителя (4).
9. Поворачивают главное приводное колесо по часовой стрелки, пока штифт, вставленный в вспомогательный счетчик, не упрется в упор (четыре поворота).
10. Число, появившиеся в окошках отображения результата, – искомое произведение 10456 на 472 (10456 х 472 = 4 935 232).
При делении, сначала, в калькулятор Лейбница вводится делимое с помощью циферблатов, и один раз поворачивается главное приводное колесо по часовой стрелке. Затем, с помощью циферблатов вводится делитель, и главное приводное колесо начинает вращаться против часовой стрелки. При этом результат деления – это количество оборотов главного приводного колеса, а в окошках отображения результатов индицировался остаток от деления.
Если делимое много больше делителя, то для ускорения деления используют сдвиг делителя на необходимое количество разрядов влево с помощью вспомогательного приводного колеса. При этом, во время подсчета количества оборотов главного приводного колеса, необходимо учитывать сдвиг (один оборот главного приводного колеса при сдвиге подвижной части калькулятора Лейбница на одну позицию влево приравнивается к десяти оборотам главного приводного колеса).
Рассмотрим принцип работы калькулятора Лейбница на примере деления 863 на 64:
1. С помощью циферблатов вводим делимое (863).
2. Поворачиваем ручку главного приводного колеса по часовой стрелки один раз.
3. С помощью циферблатов вводим делитель (863).
4. Сдвигаем движущуюся часть калькулятора Лейбница на одну позицию влево с помощью вспомогательного приводного колеса.
6. Сдвигаем движущуюся часть калькулятора Лейбница на одну позицию вправо с помощью вспомогательного приводного колеса.
Сложение осуществляется следующим способом:
1. С помощью установки циферблатов в необходимое положение, вводится первое слагаемое
2. Поворачивается ручка главного приводного колеса по часовой стрелки один раз.
3. Вводится второе слагаемое по той же технологии, как и первое.
4. Еще раз поворачивается ручка главного приводного колеса.
5. В окне результата отображается результат сложения.
Для вычитания необходимо:
1. С помощью установки циферблатов в необходимое положение, вводится уменьшаемое.
2. Поворачивается ручка главного приводного колеса по часовой стрелки один раз.
3. С помощью циферблатов вводится вычитаемое.
4. Поворачивается ручка главного приводного колеса один раз против часовой стрелки.
5. В окне результата отображается результат вычитания.
Идеи, изложенные Лейбницем, имели большое количество последователей. Так, в конце 18 века над усовершенствованием калькулятора работали Вагнер и механик Левин, а после смерти Лейбница – математик Тоблер. В 1710 году машину, аналогичную калькулятору Лейбница, построил Буркхардт. Усовершенствованием изобретения занимались и Кнутцен, и Мюллер, и другие выдающиеся ученые того времени.
Машина Готфрида Лейбница
РЕФЕРАТ
на тему:
«История развития вычислительной техники»
лицеистка ІІ-В-2 курса
СОДЕРЖАНИЕ
1. Счетные устройства до появления ЭВМ.. 3
1.1 Домеханический период. 3
1.1.1. Счет на пальцах. 3
1.1.2. Счет на камнях. 3
1.1.3. Счет на Абаке. 3
1.1.4. Палочки Непера. 4
1.1.5. Логарифмическая линейка. 5
1.2. Механический период. 6
1.2.2. Машина Готфрида Лейбница. 7
1.2.3. Перфокарты Жаккара. 8
1.2.4. Разностная машина Чарльза Бэббиджа. 8
1.2.5. Герман Холлерит. 10
1.2.6. Конрад Цузе. 10
1.2.7. Говард Айкен. 11
2. Электронно-вычислительный период. 12
2.1. Аналоговые вычислительные машины (АВМ) 12
2.2. Электронные вычислительные машины (ЭВМ) 13
2.3. Аналого-цифровые вычислительные машины (АЦВМ) 18
3. хронологическая таблица. 18
4. Список литературы.. 24
Счетные устройства до появления ЭВМ
Домеханический период
Счет на пальцах
Счет на пальцах, несомненно, самый древний и наиболее простой способ вычисления. Обнаруженная в раскопках так называемая «вестоницкая кость» с зарубками, оставленная древнем человеком ещё 30 тыс. лет до нашей эры, позволяет историкам предположить, что уже тогда предки современного человека были знакомы с зачатками счета. У многих народов пальцы рук остаются инструментом счета и на более высоких ступенях развития. К числу этих народов принадлежали и греки, сохраняющие счет на пальцах в качестве практического средства очень долгое время.
Счет на камнях
Чтобы сделать процесс счета более удобным, первобытный человек начал использовать вместо пальцев небольшие камни. Он складывал из камней пирамиду и определял, сколько в ней камней, но если число велико, то подсчитать количество камней на глаз трудно. Поэтому он стал складывать из камней более мелкие пирамиды одинаковой величины, а из-за того что на руках десять пальцев, то пирамиду составляли именно десять камней.
Счет на Абаке
Во времена древнейших культур человеку приходилось решать задачи, связанные с торговыми расчетами, с исчислением времени, с определением площади земельных участков и т.д. Рост объемов этих расчетов приводили даже к тому, что из одной страны в другую приглашались специально обученные люди, хорошо владевшие техникой арифметического счета. Поэтому рано или поздно должны были появиться устройства, облегчающие выполнение повседневных расчетов.
Так в Древней Греции и в Древнем Риме были созданы приспособления для счета, называемые абак (от греческого слова abakion – “дощечка, покрытая пылью”). Абак называют также римскими счетами. Вычисления на них проводились путем перемещения счетных костей и камешков (калькулей) в полосковых углублениях досок из бронзы, камня, слоновой кости, цветного стекла. В своей примитивной форме абак представлял собой дощечку (позднее он принял вид доски, разделенной на колонки перегородками). На ней проводились линии, разделявшие ее на колонки, а камешки раскладывались в эти колонки по тому же позиционному принципу, по которому кладется число на наши счеты. Эти счеты сохранились до эпохи Возрождения.
В странах Древнего Востока (Китай, Япония, Индокитай) существовали китайские счеты. На каждой нити или проволоке в этих счетах имелось по пять и по две костяшки. Счет осуществлялся единицами и пятерками.
В России для арифметических вычислений применялись русские счеты, появившиеся в 16 веке, но кое-где счеты можно встретить и сегодня.
Палочки Непера
Первым устройством для выполнения умножения был набор деревянных брусков, известных как палочки Непера. Они были изобретены шотландцем Джоном Непером (1550-1617гг.). На таком наборе из деревянных брусков была размещена таблица умножения. Кроме того, Джон Непер изобрел логарифмы.
Логарифмическая линейка
Развитие приспособлений для счета шло в ногу с достижениями математики. Вскоре после открытия логарифмов в 1623 г. была изобретена логарифмическая линейка.
Логарифмической линейки была суждена долгая жизнь: от 17 века до нашего времени. Вычисления с помощью логарифмической линейки производятся просто, быстро, но приближенно. И, следовательно, она не годится для точных, например финансовых, расчетов.
Механический период
Эскиз механического тринадцатиразрядного суммирующего устройства с десятью колесами был разработан еще Леонардо да Винчи (1452— 1519). По этим чертежам в наши дни фирма IBM в целях рекламы построила работоспособную машину.
Первая механическая счетная машина была изготовлена в 1623 г. профессором математики Вильгельмом Шиккардом (1592—1636). В ней были механизированы операции сложения и вычитания, а умножение и деление выполнялось с элементами механизации. Но машина Шиккарда вскоре сгорела во время пожара. Поэтому биография механических вычислительных устройств ведется от суммирующей машины, изготовленной в 1642 г. Блезом Паскалем.
В 1673 г. другой великий математик Готфрид Лейбниц разработал счетное устройство, на котором уже можно было умножать и делить.
В 1880г. В.Т. Однер создает в России арифмометр с зубчаткой с переменным количеством зубцов, а в 1890 году налаживает массовый выпуск усовершенствованных арифмометров, которые в первой четверти 19-ого века были основными математическими машинами, нашедшими применение во всем мире. Их модернизация «Феликс» выпускалась в СССР до 50-х годов.
Мысль о создании автоматической вычислительной машины, которая бы работала без участия человека, впервые была высказана английским математиком Чарльзом Бэббиджем (1791—1864) в начале XIX в. В 1820—1822 гг. он построил машину, которая могла вычислять таблицы значений многочленов второго порядка.
Машина Блеза Паскаля.
Считается, что первую механическую машину, которая могла выполнять сложение и вычитание, изобрел в 1646г. молодой 18-летний французский математик и физик Блез Паскаль. Она называется «паскалина».
Машина Готфрида Лейбница
Следующим шагом было изобретение машины, которая могла выполнять умножение и деление. Такую машину изобрел в 1671 г. немец Готфрид Лейбниц. Хоть машина Лейбница и была похожа на «Паскалину», она имела движущуюся часть и ручку, с помощью которой можно было крутить специальное колесо или цилиндры, расположенные внутри аппарата. Такой механизм позволил ускорить повторяющиеся операции сложения, необходимые для умножения. Само повторение тоже осуществлялось автоматически.
Перфокарты Жаккара
Французский ткач и механик Жозеф Жаккар создал первый образец машины, управляемой введением в нее информацией. В 1802 г. он построил машину, которая облегчила процесс производства тканей со сложным узором. При изготовлении такой ткани нужно поднять или опустить каждую из ряда нитей. После этого ткацкий станок протягивает между поднятыми и пущенными нитями другую нить. Затем каждая из нитей опускается или поднимается в определенном порядке и станок снова пропускает через них нить. Этот процесс многократно повторяется до тех пор, пока не будет получена нужная длина ткани с узором. Для задания узора на ткани Жаккар использовал ряды отверстий на картах. Если применялось десять нитей, то в каждом ряду карты предусматривалось место для десяти отверстий. Карта закреплялась на станке в устройстве, которое могло обнаруживать отверстия на карте. Это устройство с помощью щупов проверяло каждый ряд отверстий на карте. Информация на карте управляла станком.
История математики. Лекция 11. Лейбниц. Занятия математикой.
Александр Савельевич Штерн 
Оригинал взят тут.
Лекция № 11.
Лейбниц. Занятия математикой: начало и триумф.
Здесь хочется сделать преамбулу. Имела место дискуссия, в которой участвовали я и один мой весьма уважаемый коллега. Смысл дискуссии был в следующем. Кто же всё-таки придумал функцию: Ньютон и Лейбниц, понимавшие её, как произвольную переменную величину, зависящую от другой переменной величины, или Вейерштрасс, научившийся смотреть на неё, как на отображение из одного множества в другое. Мне кажется, что шаг, сделанный в 17-м веке. куда более революционен.
Лейбниц всегда интересовался математикой и современной ему философией, но серьёзной возможности изучить эти науки в Майнце, который в культурном отношении был глубокой провинцией Европы, он не имел. Такая возможность представляется ему только в Париже. Лейбниц изучает труды Декарта и Паскаля, посещает семинар Мерсенна, знакомится с лидерами Пор-Рояля. Очень много времени проходит в общении с Христианом Гюйгенсом, жившим тогда в Париже великим голландским физиком.
Первым его крупным достижением, имевшим прямое отношение к математике, стало значительное усовершенствование арифмометра Паскаля. Машина Паскаля умела только складывать и вычитать, а умножать и делить не умела. Лейбниц, преодолев значительные технические трудности, научил арифмометр умножать, делить и извлекать квадратные корни. В машине был реализован алгоритм умножения в столбик. Сдвиг числа на разряд, который производится при таком умножении, осуществлялся с помощью некоторой специальной каретки. Машина была сконструирована и изготовлена в кратчайшие сроки, буквально за несколько месяцев. Из Парижа Лейбниц ненадолго съездил в Лондон, где продемонстрировал своё изобретение членам английской академии наук. Впечатление было очень велико: почти немедленно 27-летний Лейбниц становится её членом.
Вернувшись в Париж, Лейбниц изучает работы Паскаля, Декарта, Ферма и других математиков, посвящённые изучению кривых. Основную проблематику этих работ мы уже обсуждали: построение касательных, вычисление площадей, определение центров тяжести и т.д. Результатом этих изучений стало построение дифференциального исчисления.
В это почти невозможно поверить. Человек, чьё знание математики почти соответствовало уровню её развития трёхсотлетней давности, за три года смог изучить эту науку так, что стал создателем абсолютно новой математической теории. Причём, это была такая теория, которую наука напряжённо ждала. У Лейбница появился весь аппарат классического дифференциального исчисления: он ввёл понятие функции и производной, выписал таблицу производных, сформулировал правило дифференцирования произведения и дифференцирования сложной функции, ввёл понятие интеграла, знак интеграла и знак дифференциала, научился использовать ряды для интегрирования функций и решения дифференциальных уравнений.
Как это получалось, как работала мысль Лейбница, очень хорошо показывает один пример, который разбирает один из крупнейших современных математиков академик В.И. Арнольд в своей книге «Гюйгенс и Барроу, Ньютон и Гук».
«Способ мышления у Лейбница был такой. Он считал, что вся математика, так же как и вся наука, находится внутри нас, и с помощью одной философии можно до всего додуматься, если внимательно прислушаться к процессам, происходящим внутри нашего разума. Таким методом он открывал различные законы и иногда очень успешно. Например, он открыл, что d(x+y)=d(x)+d(y), и это замечательное открытие немедленно заставило его задуматься о том, чему же равен дифференциал произведения. В соответствии с универсальностью своих размышлений он быстро пришёл к выводу, что … должна иметь место формула d(xy)= d(x)d(y). Но через некоторое время он убедился, что это приводит к каким-то неприятным последствиям, и нашёл правильную формулу, … которая теперь называется правилом Лейбница. Никому из индуктивно мыслящих математиков … никогда не пришла бы в голову первоначальная гипотеза Лейбница, так как им было совершенно ясно, чему равен дифференциал произведения из простой картинки… Но для схоласта Лейбница такой алгебраический ход мысли очень типичен» (стр. 36-37)
Это рассуждение даёт достаточно убедительную модель мышления Лейбница. Есть некоторый математический факт, который нам хочется обобщить или построить аналог. Как это сделать? Способов может быть много, но как выбрать нужный? Лейбниц всегда предлагает выбирать так, как требует чувство гармонии, так, чтобы общая картина оказывалась стройной и завершённой. Переход от формулы дифференцирования суммы к неправильной формуле дифференцирования произведения гораздо естественнее, чем к правильной. Если бы была верна первая из этих формул, то дифференциальное исчисление было бы и в самом деле гораздо завершённее, чем на самом деле. Если по таком пути построения математической теории пойдёт человек средних способностей, то возникнет некоторая псевдотеория, в которой верные факты будут чередоваться с «естественными», но неверными.
Но Лейбниц был математическим гением, и его «математическая совесть» беспощадно отсекала неверные, хотя и эстетически соблазнительные рассуждения. В то же время источником новых идей было, по-видимому, некоторое смутное ощущение красоты и завершённости. Определённую роль это чувство играет в работе любого математика, но, наверное, ни у кого кроме Лейбница оно не было до такой степени определяющим. Именно поэтому в таких количествах он производил символы, определения, формулы и т.д.
Все лекции курса «История математики в контексте истории культуры» по метке «ИМ в контексте ИК»
Счетная машина Лейбница: принцип действия, год создания и фото
Колесо Лейбница
Колесо или ступенчатый барабан представляет собой цилиндр с набором зубцов инкрементных длин, которые при соединении со счетным колесом могут использоваться в вычислительном двигателе класса механических калькуляторов. Изобретенный Лейбницем в 1673 году, он использовался в течение трех столетий до появления электронного калькулятора в середине 1970-х годов.
Лейбниц построил машину, названную ступенчатым реконером (или машиной Лейбница), на основе конструкции ступенчатого барабана в 1694-м. Он был широко прославлен Томасом де Кольмаром, когда он использовал его спустя полтора века в своем арифмометре, первой серийной вычислительной машине. Он также использовался в калькуляторе Курта, очень популярном портативном калькуляторе, представленном во второй половине 20-го века.
Если соединить колесо Лейбница со счетным колесом, свободным для перемещения вверх и вниз по его длине, счетное колесо может зацепляться с любым количеством зубов. Фото машины Лейбница вы можете увидеть в этой статье. Многие энтузиасты пытаются воссоздать это чудо 17-го века в домашних условиях, используя подручные материалы.
Машина Лейбница: принцип работы
Этот примитивный калькулятор обладал девятью зубцами, соединенными с красным счетным колесом.
В вычислительном устройстве арифмометра имеется набор связанных колес, соединенных с рукояткой кривошипа. Каждый поворот рукоятки кривошипа поворачивает все колеса на один полный оборот. Входные ползунки перемещают подсчетные колеса вверх и вниз по колесам, которые сами связаны механизмом переноса.
Начиная с конца девятнадцатого века барабаны Лейбница, извлеченные из этого механизма и используемые во всех прото-калькуляторах, были частично вытеснены штифтами, которые по своей функции похожи, но обладали более компактным видом. Ступенчатые барабаны оставались основной технологией для электромеханических калькуляторов до разработки чисто электронных аналогов в прошлом веке.
Счетная машина была создана на базе механизма, который изобрел Лейбниц и который теперь называется машиной Лейбница. Неясно, сколько было сделано разных экземпляров этого первого в мире калькулятора. Некоторые источники утверждают, что их было 12. В этом статье описывается сохранившийся 16-значный прототип, хранящийся в Ганновере.
Описание
Машина имеет длину около 67 см (26 дюймов), выполнена из полированной латуни и стали, смонтирована в дубовом корпусе. Она состоит из двух прикрепленных параллельных частей. Секция аккумулятора находилась сзади, клавиатура вмещала 16 десятичных цифр и 8-разрядную секцию ввода спереди.
Секция ввода имеет 8 наборов с кнопками для установки номера операнда, телефонный диск справа, чтобы установить цифру множителя, и кривошип на передней панели для выполнения расчета. Результат исчисления появлялся в 16-значном окошке задней части аккумулятора.
Секция ввода монтируется на рельсах и может перемещаться вдоль аккумуляторной секции с помощью кривошипа на левом конце, который вращает червячную шестерню, чтобы изменить выравнивание цифр операндов с помощью цифр аккумулятора.
Существует также индикатор переноса с десятками и элемент управления для установки нолей при расчетах.
Сложение и вычитание
Сложение или вычитание выполняется за один шаг с поворотом рукоятки. Умножение и деление выполняются с помощью клавиш умножителя или делителя в процедуре, эквивалентной знакомым методам длительного умножения и длительного разделения, которые преподаются в школе. Последовательности этих операций могут выполняться по числу в аккумуляторе: например, он может вычислять корни с помощью серии разделов и дополнений. Для своего времени счетная машина Лейбница была очень прогрессивным механизмом. Ее компоненты, как уже писалось выше, использовались в механических калькуляторах на протяжении целых 300 лет, что кажется совершенно невероятным.
История
Лейбниц разработал идею вычислительной машины в 1672 году в Париже благодаря шагомеру. Позже он узнал о машине Блеза Паскаля, когда прочитал его трактат Pensees. Он сосредоточился на расширении механизма Паскаля, чтобы он мог умножать и делить. 1 февраля 1673 года он представил деревянную модель Лондонскому королевскому обществу и получил большую поддержку. В письме от 26 марта 1673 года Иоганну Фридриху, где он упомянул о представлении в Лондоне, Лейбниц описал цель «арифметической машины» как составление расчетов leicht, geschwind, gewiß, то есть легко, быстро и точно. Лейбниц также добавил, что теоретически рассчитанные числа могут быть еще большими, если бы размер машины был как следует скорректирован. Первая предварительная латунная машина Готфрида Лейбница была построена между 1674 и 1685 годами. Его так называемая старая машина была построена между 1686 и 1694 гг. «Более молодая машина», сохранившаяся до наших времен и выставленная в Ганновере, была построена с 1690 по 1720 год.
В 1775 году «младшая машина» была отправлена в Геттингенский университет для ремонта и забыта. В 1876 году рабочие нашли ее в мансарде университетского здания в Геттингене. Она была возвращена в Ганновер в 1880 году. С 1894 по 1896 год Артур Буркхардт, основатель крупной немецкой калькуляторной компании, восстановил ее.
Функционал
Машина выполняет умножение путем повторного добавления и деление путем повторного вычитания. Основная выполняемая операция заключается в том, чтобы добавить (или вычесть) номер операнда в регистр накопителя столько раз, сколько требуется (чтобы вычесть, рабочий кривошип поворачивается в противоположном направлении). Количество дополнений (или вычитаний) контролируется множителем. Он работает, как телефонный диск, с десятью отверстиями по окружности с номерами от 0 до 9. Чтобы умножить на одну цифру, в соответствующее отверстие на циферблате вставлен стилус в форме ручки, а кривошип повернут. Циферблат мультипликатора поворачивается по часовой стрелке, машина выполняет одно добавление для каждого отверстия, пока стилус не остановится в верхней части циферблата. Результат появляется в окнах накопителя.
Повторные вычитания выполняются аналогично, за исключением того, что множительный циферблат поворачивается в противоположном направлении, поэтому используется второй набор цифр, выделенный красным цветом. Чтобы выполнить одно сложение или вычитание, множитель просто устанавливается на единицу. Как можно понять, вычислительная машина Лейбница была крайне удобной для своего времени.
Сложное умножение
Деление
Операция деления на машине Лейбница проводится несколько иным способом:
Калькулятор Паскаля
Калькулятор Паскаля был особенно успешным в части механизма переноса, который добавляет от 1 до 9 на одном циферблате, а когда он меняется от 9 до 0, переносит 1 в следующую таблицу, находящуюся рядом. Паскаль был первым ученым, который переработал и адаптировал для своей цели фонарный механизм, используемый в башенных часах и водяных колесах. Арифметическая машина Лейбница в известной степени стала продолжением идеи Паскаля, и его опыт был изучен и использован немецким ученым для создания собственного механического шедевра.