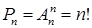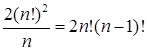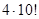8 человек должны сесть в 2 автомобиля причем в каждый не менее 3 человек
8 человек должны сесть в 2 автомобиля причем в каждый не менее 3 человек
Для вычисления вероятностей нам нужно будет подсчитывать количество вариантов наступления тех или иных событий. Поэтому перед изучением теории вероятностей рассмотрим некоторые понятия, связанные с комбинаторикой. Данная глава носит вспомогательный характер. Если вы изучали этот раздел математики раньше, можно её пропустить.
1.1. Основные определения
Материал этого раздела изложен в книге.
1.2. Перестановки
1.3. Размещения
1.4. Сочетания
Пример 1.16. Сколько существует вариантов разбиения студенческой группы из 25 человек на две подгруппы, в каждой из которых от 10 до 15 человек?
1.5. Разбиения
Функция MATLAB для генерации полного списка разбиений partitions размещена в этом архиве. Распакуйте архив в какую-нибудь папку, доступную MATLAB. Ниже приведен пример вычисления количества разбиений и генерации полного списка разбиений.
Пример 1.20. Сколько существует способов разбить 25 студентов на 3 подгруппы, если в каждой подгруппе должно быть не менее 8 человек?
Решение. Всего существует 3 варианта разбиения на указанные подгруппы: это на и человек. Нам нужно выбрать один из этих вариантов, поэтому применяем правило сложения. Общее число вариантов будет равно Вычисляем с помощью MATLAB.
Пример 1.21. Сколько существует способов разбить 25 студентов на 3 подгруппы, если в каждой подгруппе должно быть не менее 6 человек?
Решение. В предыдущем примере мы сразу увидели, что возможны только 3 варианта разбиения. Здесь количество вариантов значительно больше. Мы сначала должны сгенерировать все эти варианты разбиения, а потом подсчитать для каждого из них количество разбиений и сложить. Поручим эту работу MATLAB. Вначале мы проверяем, возможны ли вообще какие либо варианты разбиения. Если такие варианты есть, находим их все. Для этого с помощью функции fullfact (полный факторный эксперимент) генерируем все возможные сочетания количеств студентов в подгруппах, а затем отбираем те из них, для которых сумма равна 25. В данном случае выясняется, что всего таких вариантов 36. Теперь для каждого из них по формуле (1.10) вычисляем и складываем. Для ускорения счета все нужные факториалы вычисляем один раз.
1.6. Перестановки с повторениями
В следующем примере мы находим количество перестановок с повторениями для больших размеров задачи, а для задачи небольшого размера, кроме того, и строим все перестановки с повторениями.
1.7. Размещения с повторениями
Рассмотрим алгоритмы построения полного списка размещений. В первой схеме проще всего построить вначале все перестановки с повторениями (функция perms ), затем в полученном массиве оставить k первых столбцов, и, наконец, удалить повторяющиеся строки.
Схема 3 отличается от 2-й тем, что вместо всех элементов исходного множества нужно использовать неповторяющиеся.
Пример 1.26. Сколько различных 6 значных шифров можно составить из цифр числа 112223345, если цифры могут повторяться, но 1 − не более 2 раз, 2 − не более 3 раз,
Решение. В задачах с такой формулировкой исходное множество вообще может быть не задано, а просто сказано, что такой-то предмет может повторяться не более такого-то количества раз. Здесь после выборки очередного числа исходное множество не восстанавливается до исходного, поэтому имеем 1-ю схему. Готовой формулы у нас нет − считаем количество вариантов.
1.8. Сочетания с повторениями
Для построения списка всех сочетаний по схеме 2 можно с помощью функции fullfact построить все размещения, как это было сделано в разделе 1.7, затем каждую строку рассортировать, а потом удалить повторяющиеся строки. В следующем примере сначала по формуле (1.15) находится число сочетаний с повторениями для больших значений n и k, а затем генерируется полный список сочетаний с повторениями для небольших n и k.
Для генерации всех сочетаний мы опять воспользуемся списком размещений, каждое из которых сортируем, чтобы выявить одинаковые. Затем оставляем только по одному экземпляру каждого сочетания. В следующем примере сначала по формуле (1.16) находится число сочетаний с повторениями для больших значений m и k, а затем генерируется полный список сочетаний с повторениями для небольших m и k.
Пример 1.29. В урне имеется 5 белых шаров, 3 красных и 2 черных. Наугад вынимается 3 шара. Сколько существует вариантов раскраски этих троек?
1.9. Решение задач
Пример 1.41. В фойе театра 4 друга одновременно сдали куртки в раздевалку и получили 4 номерка. Сколько существует вариантов раздачи номерков, при которых ни один из них не получит назад свою куртку?
Решение. Всего есть 4! вариантов раздачи номерков. Очевидно, только 1 из них является правильным (пусть это будет основная перестановка). Нет ни одного варианта, когда ровно 3 человека получат свои номерки (почему?). Для 2 угадываний количество вариантов ещё считается легко, а вот для 1 и 0 уже достаточно трудно. Мы не выводили общей формулы для количества беспорядков, поэтому построим общий список перестановок, а затем отберём нужные и подсчитаем их количество.
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Проверьте решение задач по комбинаторике
 |
Последний раз редактировалось ЕкатеринаУ 09.02.2007, 15:23, всего редактировалось 1 раз.
Проверьте, пожалуйста, решение задач по комбинаторике, и если Вы видете ошибки, укажите на них.
Извините, не смогла разобраться как пользоваться [math], приходится формулы в текстовом виде писать.
1. Колода карт насчитывает 52 карты. Сколькими способами можно сдать одному игроку 4 карты?
Решение:
1 вариант
Количество способов, которыми можно сдать 4 карты из 52 найдем по формуле «число размещений»
A(52, 4) = 52!/48! = 52*51*50*49 = 6497400
P/s: В задаче не сказано важен ли порядок карт, поэтому я решила посчитать по формуле размещений.
2 вариант
1-ю карту можно сдать игроку 52 способами.
2-ю карту можно сдать игроку 51 способами (учитывая, что одна карта уже сдана).
3-ю карту можно сдать игроку 50 способами.
4-ю карту можно сдать игроку 49 способами.
Тогда используя принцип умножения, получаем, что количество способов сдачи одному игроку 4 карты из 52 равно
n = 52*51*50*49 = 6497400.
2. Сколькими способами из 5 супружеских пар можно отобрать 4 человека, если:
а) в число отобранных должны входить 2 мужчин и 2 женщины;
б) никакая супружеская пара не должна входить в это число.
Решение:
а) Сначала выберем из мужчин двух человек.
Считаем, что порядок мужчин не важен, значит, находим число сочетаний двух мужчин из
пяти по формуле
n1 = C(5,2) = 5!/(2!*3!) = 10.
Точно также посчитаем сколькими способами можно выбрать двух женщин из пяти.
Аналогично выбору мужчин способов будет n2 = C(5,2)=5!/(2!*3!) = 10.
Тогда количество способов, которыми можно отобрать из 5 супружеских пар 2 мужчин и
2 женщин равно n = n1*n2 = 10*10 = 100.
| Супермодератор |
 |
|
Хорошо, напишу два варианта.
| Супермодератор |
|
|
3. Подрядчику нужны 4 специалиста, а к нему обратились 10. Сколькими способами он может выбрать четверых?
В данном случае порядок наверно не важен, поэтому использую формулу сочетаний
Добавлено спустя 2 минуты 5 секунд:
Хороошо, но я понимаю (более менее) в чем разница, а человек для которого я решаю, не уверена, что понимает. Поэтому и пишу подробно.
Добавлено спустя 3 минуты 15 секунд:
>> Друг
>> Для записи математических выражений используйте тег 
Добавлено спустя 8 минут 17 секунд:
4. Для участия в соревнованиях тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если:
а) два определенных мальчика должны войти в команду;
б) нет никаких ограничений.
б) по формуле сочетаний С(10, 5) = 10!/(5!*5!) = 252
Добавлено спустя 5 минут 46 секунд:
5. В автомашине 7 мест. Сколькими способами 7 человек могут разместиться в машине, если занять место водителя могут только 3 из них?
Здесь я точно не знаю, но думаю так:
На место водителя сажаем одного человека. Остальные 6 могут рассесться 6! способами (по формуле перестановок).
Затем меняем водителя и остальных рассаживаем 6! способами.
И третий раз повторяем тоже.
Получаем, 3*6! = 3 * 720 = 2160 способов.
Добавлено спустя 8 минут 42 секунды:
6. 8 человек должны расположиться в двух комнатах, причем в каждой должно быть, по крайней мере, 3 человека. Сколькими способами это можно сделать?
Мыслей почти ноль, но некоторые размышления.
В одной комнате может располагаться максимум 5 человек,
Количество способов выбрать из 8 человек 5 (по формуле сочетаний) равно С(8, 5) = 56.
Тогда в другой максимум 3, С(8, 3) = 56.
А дальше сложить результаты или умножить.
Бред какой-то, но ничего другого на ум не идет.
| Заслуженный участник |
 |
В 6 задаче ещё надо учесть, что может быть по 4 человека в комнатах. Результаты надо сложить.
Добавлено спустя 6 минут 23 секунды:
Только по-моему слова «в другой» здесь не очень правильные. Я-бы рассмотрела для одной комнаты выбор 3, 4 и 5 человек из 8. Если комнаты различаются, то надо умножить на 2.
|
4. Для участия в соревнованиях тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если:
а) два определенных мальчика должны войти в команду;
б) нет никаких ограничений.
б) по формуле сочетаний С(10, 5) = 10!/(5!*5!) = 252
Я конечно могу и ошибаться, но мне кажется тут ошибка. Ведь порядок выбора мальчиков не играет роли. Соответственно и ответ будет 
Так как первых двух мальчиков выбираем однозначно, а остальных без учета порядка выбора.
Добавлено спустя 10 минут 27 секунд:
6. 8 человек должны расположиться в двух комнатах, причем в каждой должно быть, по крайней мере, 3 человека. Сколькими способами это можно сделать?
Мыслей почти ноль, но некоторые размышления.
В одной комнате может располагаться максимум 5 человек,
Количество способов выбрать из 8 человек 5 (по формуле сочетаний) равно С(8, 5) = 56.
Тогда в другой максимум 3, С(8, 3) = 56.
А дальше сложить результаты или умножить.
Бред какой-то, но ничего другого на ум не идет.
Почти так но просто надо расмотреть все варианты. А их всего три: в одной комнате 3 во второй 5, наоборот и в каждой по 4. Итого 
|
её решение я написала так (текст подправила после ваших сообщений)
5. 8 человек должны расположиться в двух комнатах, причем в каждой должно быть, по крайней мере, 3 человека. Сколькими способами это можно сделать?
Решение:
Есть 3 варианта расположения человек по комнатам: 5 – 3, 4 – 4, 3 – 5.
Каждый из вариантов расположения человек, исключает другой, значит, задачу можно переформулировать следующим образом:
Из 8 человек в комнате могут находиться или 3 человека, или 4, или 5, при этом порядок людей не важен. Сколькими способами можно это можно сделать?
В этом случае применяем принцип сложения для подсчета всех способов расположения людей.
способами можно расположить 8 человек по двум комнатам, при условии, что в каждой должно быть не меньше 3 человек.
Насчет 4-ой задачи, я поняла, что рассуждала совершенно не правильно, спасибо, что подсказали.
В задаче 5 я немного поменяла объснительный текст, скажите он стал точнее или я ушла в дебри (в сторону от сути задачи):
5. В автомашине 7 мест. Сколькими способами 7 человек могут разместиться в машине, если занять место водителя могут только 3 из них?
Решение:
Сажаем одного человека на место водителя (из числа тех трех, что могут занимать его место), остальные 6 человек могут меняться местами 6! способами (число перестановок ). Меняем водителя, и оставшиеся также рассаживаются 6! способами. Также делаем и в 3 раз.
Так как, место водителя может занимать только один человек, то каждый из вариантов исключает другой, значит здесь применим принцип сложения.
способов расположения 7 человек в машине, если место водителя могут занимать только 3 из них.
| Заслуженный участник |
|
|
| Заслуженный участник |
|
, если каждый раз выбираем из 8
, если отобраное количество уже известно и лежит в заданом диапзоне
|
| Заслуженный участник |
|
Последний раз редактировалось Capella 14.02.2007, 01:35, всего редактировалось 1 раз.
Нет. Первая формула считает такой расклад: у Вас есть изначально 8 кубиков, из которых Вы выбираете не кладя назад Ваши множества, т.е. упорядоченое расположение (в дальнейшем ур) 1 кубика из 8, ур 2 кубиков из 8, ур 3 кубиков из 8 и т.д. до ур 8 кубиков из 8. Их объединение даёт Вам все варианты.
Вторая формула считает так (я не думаю, что она спрашивается, скорее всего первый метод, но я Вам её всё равно привожу): У Вас отобрано 8 кучек для 8 экспериментов: 1 кубик, 2 кубика, 3 кубика и т.д. Уже внутри этих кучек делаем упорядоченое расположение. Назад мы опять не кладём. Далее опять образуем сумму. Я сделала этот вариант, поскольку не очень хорошо поняла смысл выделеного слова в Вашем посте:
т.е. они уже отобраны количествено или их только будут отбирать из 8
|
| Заслуженный участник |
|
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?
Имеем набор <я, я, г, г, г>. Всего перестановок пятиэлементного множества 5!, но мы не должны учитывать перестановки, в которых объекты одного типа меняютсяместами несколько раз, поэтому нужно поделить на возможное число таких перестановок: 2!·3!. Получаем в итоге
Задание 2.
В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
Т.к. все пассажиры должны ехать в разных вагонах, требуется отобрать 4 вагона из 9 с учетом порядка (вагоны отличаются №), эти выборки – размещения из n различных элементов по m элементов, где n=9, m=4. Число таких размещений находим по формуле:
Ответ: 3024 способами можно рассадить в поезде 4 человек.
Задание 3.
Имеем 14 претендентов и 13 рабочих мест. Сначала выберем работников на первую специальность, то есть 4 женщин из 6:
Далее независимо аналогичным образом выберем мужчин на вторую специальность:
Осталось 2 женщины, 2 мужчин и 3 вакантных места, которые, по условию, могут занять любые из четырех оставшихся человек. Это может быть сделано 2 вариантами:
1. 1 женщина и 2 мужчин (выбираем женщину C 1 2=2 способами)
2. 1 мужчина и 2 женщины (выбираем мужчину C 1 2=2способами).
В итого получаем 15·28(2 + 2) = 1680 способов.
07. Перестановки
Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.
Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.
Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.
Число перестановок n различных элементов обозначают символом Pn и равно
Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?
Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем
P6P4 = 720×24 = 17280.
Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?
Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно
4! – 3! = 3×3! = 3×1×2×3 = 18.
Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?
Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем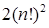 
.
Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.
Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?
5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.
Ответ: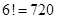 
.
5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?
Ответ: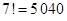 
.
5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?
Ответ: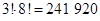 
.
5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?
Ответ: 
5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?
Ответ: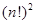 
.
5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?
Ответ: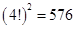 
.
5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?
Ответ: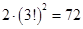 
.
5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.