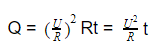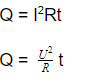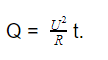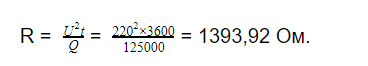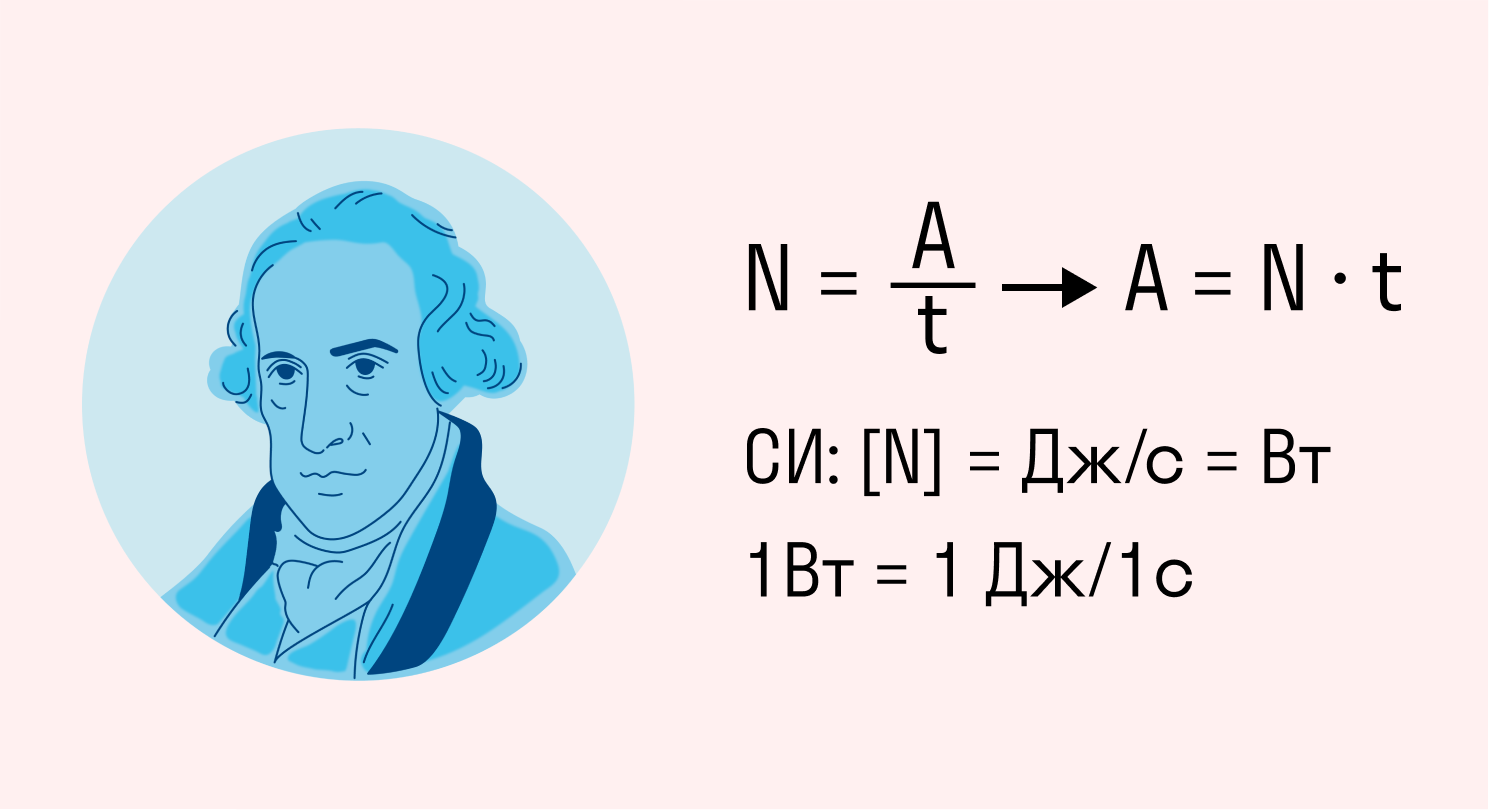a uit что за формула

19.12.202303.07.2023 admin 0 Comments

Формула мощности тока. Фактическая и номинальная мощность. КПД электрического прибора

Действие всех известных электрических приборов происходит за счет электрической энергии. В результате этого мы получаем свет, тепло, звук, механическое движение, то есть разные виды энергии. В этой статье мы рассмотрим и изучим такое физическое понятия, как мощность электрического тока.

Формулы мощности тока

Под мощностью тока так же, как и в механике, понимают работу, которая выполняется за единицу времени. Рассчитать мощность, зная работу, которую выполняет электрический ток за некоторый промежуток времени, поможет физическая формула.

Ток, напряжение, мощность в электростатике связаны равенством, которое можно вывести из формулы A = UIt. По ней определяют работу, которую выполняет электрический ток:

P = A/t = UIt/t = UI
Таким образом, формула мощности постоянного тока на любом участке цепи выражается как произведение силы тока на напряжение между концами участка.

Единицы измерения мощности

Прибор для измерения мощности электрического тока называется ваттметр. Также формула мощности тока позволяет определять мощность с помощью вольтметра и амперметра.

1кВт·ч = 10 3 Вт·3600с = 3,6·10 6 Вт·с = 3,6·10 6 Дж.

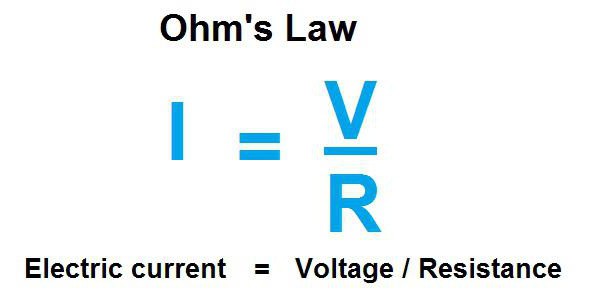
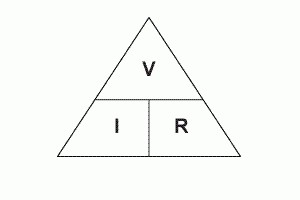
Закон Ома и мощность

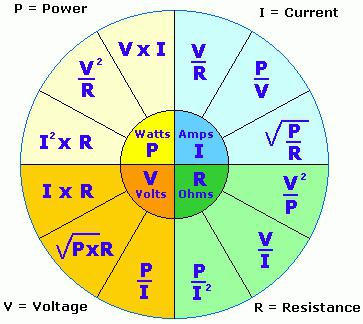
Используя закон Ома, формула мощности тока P = UI записывается в таком виде:

P = UI = U 2 /R = I 2 /R
Итак, мощность, выделяемая на проводниках, прямо пропорциональна силе тока, протекающей через проводник, и напряжению на его концах.

Фактическая и номинальная мощность

При измерении мощности в потребителе формула мощности тока позволяет определить ее фактическую величину, то есть ту, которая реально выделяется в данный момент времени на потребителе.

В паспортах различных электрических приборов также отмечают значение мощности. Ее называют номинальной. В паспорте электрического прибора обычно указывают не только номинальную мощность, но и напряжение, на которое он рассчитан. Однако напряжение в сети может немного отличаться от указанного в паспорте, например, увеличиваться. С увеличением напряжения увеличивается и сила тока в сети, а следовательно, и мощность тока в потребителе. То есть значение фактической и номинальной мощности прибора могут отличаться. Максимальная фактическая мощность электрического устройства больше номинальной. Это сделано с целью предотвращения выхода прибора из строя при незначительных изменениях напряжения в сети.

Если цепь состоит из нескольких потребителей, то, рассчитывая их фактическую мощность, следует помнить, что при любом соединении потребителей общая мощность во всей цепи равна сумме мощностей отдельных потребителей.

Коэффициент полезного действия электрического прибора

Как известно, идеальных машин и механизмов не существует (то есть таких, которые бы полностью превращали один вид энергии в другой или генерировали бы энергию). Во время работы устройства обязательно часть затраченной энергии уходит на преодоление нежелательных сил сопротивления или просто «рассеивается» в окружающую среду. Таким образом, только часть затраченной нами энергии уходит на выполнение полезной работы, для выполнения которой и было создано устройство.

Другими словами, КПД показывает, насколько эффективно используется затраченная работа при ее выполнении, например, электрическим прибором.

КПД определяется (как и в механике) по формуле:

Если известна мощность электрического тока, формулы для определения ККД будут выглядеть так:

Прежде чем определять КПД некоторого устройства, необходимо определить, что является полезной работой (для чего создано устройство), и что является затраченной работой (работа выполняется или какая энергия затрачивается для выполнения полезной работы).

Задача

Обычная электрическая лампа имеет мощность 60 Вт и рабочее напряжение 220 В. Какую работу выполняет электрический ток в лампе, и сколько вы платить за электроэнергию в течение месяца, при тарифе Т = 28 рублей, используя лампу 3 часа каждый день?
Какая сила тока в лампе и сопротивление ее спирали в рабочем состоянии?

1. Для решения данной проблемы:
а) вычисляем время работы лампы в течение месяца;
б) вычисляем работу силы тока в лампе;
в) вычисляем плату за месяц по тарифу 28 рублей;
г) вычисляем силу тока в лампе;
д) вычисляем сопротивление спирали лампы в рабочем состоянии.

2. Работу силы тока рассчитываем по формуле:

Силу тока в лампе поможет вычислить формула мощности тока:

Сопротивление спирали лампы в рабочем состоянии из закона Ома равно:

t = 30 дней · 3 ч = 90 ч;
А = 60·90 = 5400 Вт·ч = 5,4 кВт·ч;
I = 60/220 = 0,3 А;
R = 220/0,3 = 733 Ом;
В = 5,4 кВт·ч·28 к / кВт ч = 151 руб.

Ответ: А = 5,4 кВт·ч; I = 0,3 А; R = 733 Ом; В = 151 рубль.

Источник

Работа электрического тока. Закон Джоуля-Ленца.

Для определения работы, которая совершается током, проходящим по некоторому участку цепи, нужно воспользоваться определением напряжения: . Значит,

где А — работа тока; q — электрический заряд, который прошел за определенное время через исследуемый участок цепи. Подставив в последнее равенство формулу q = It, имеем:

Работа электрического тока на участке цепи является произведением напряжения на концах этого участка на силу тока и на время, на протяжении которого совершалась работа.

Закон Джоуля — Ленца гласит: количество теплоты, которое выделяется в проводнике на участке электрической цепи с сопротивлением R при протекании по нему постоянного тока I в течение времени t равно произведению квадрата тока на сопротивление и время:

Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которому удалось раскалить железную спираль, пропустив через нее электрический ток.

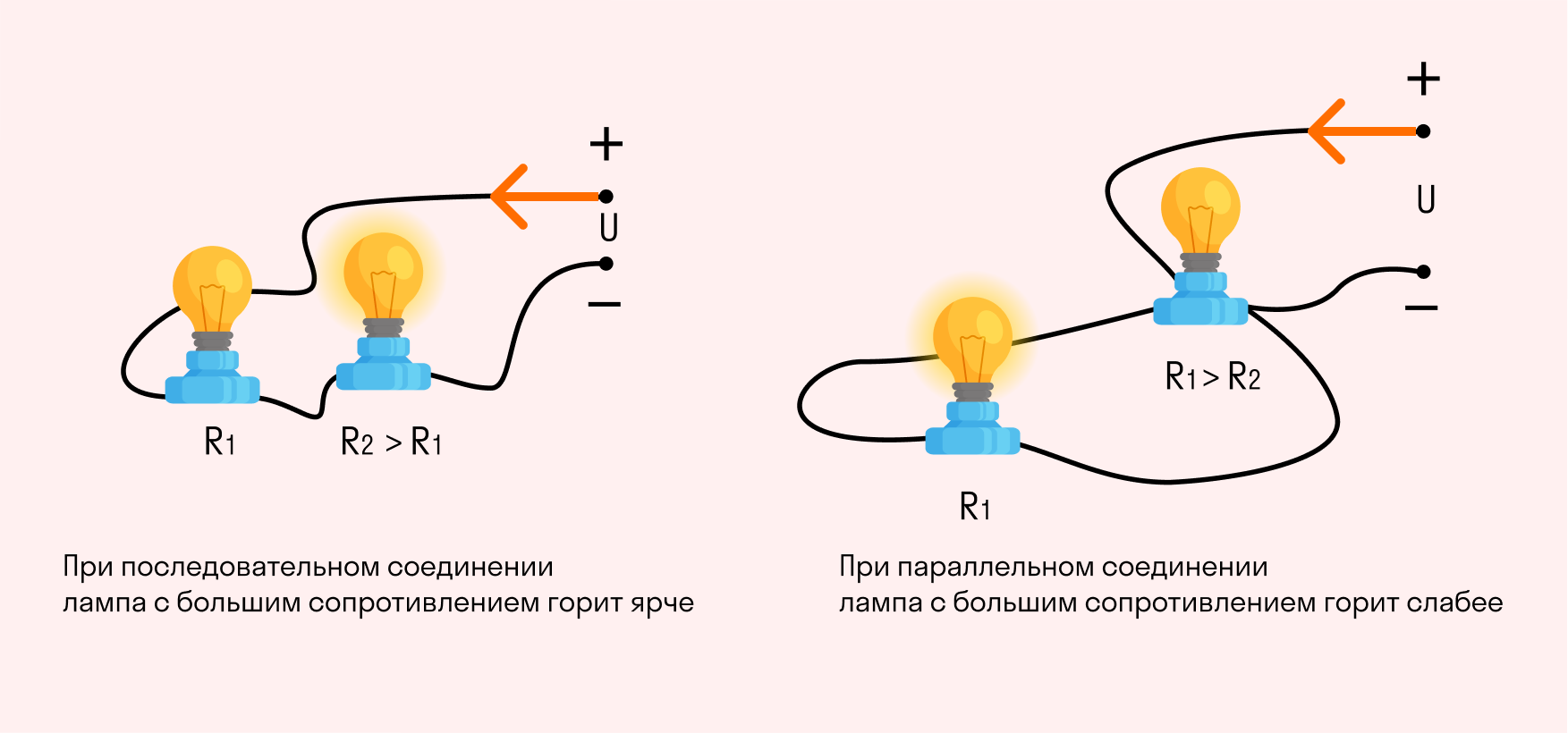
Из закона Джоуля — Ленца видно, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на проводнике с наибольшим сопротивлением. Это применяется в технике, например, для распыления металлов.

При параллельном соединении каждый проводник находятся под одинаковым напряжением, но токи в них разные. Из формулы (Q = I 2 Rt) видно, что, так как, согласно закону Ома , то

Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.

Если в формуле (А = IUt) выразить U через IR, воспользовавшись законом Ома, получим Закон Джоуля — Ленца. Это лишний раз подтверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.

Источник

Билет № 16. Работа и мощность электрического тока

Работа и мощность электрического тока. Их единицы. Формула для расчета работы и мощности электрического тока.

1)Чтобы определить работу электрического тока на каком- либо участке цепи, надо напряжение на концах этого участка цепи умножить на электрический заряд (кол-во электрического), прошедший по нему: A = Uq, где А – работа, U – напряжение, q – электрический заряд. Электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения: q = It.

Формула работы электрического тока, которой удобно пользоваться при расчетах: A = UIt.

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Работу измеряют в джоулях, напряжение – в вольтах, силу тока – в амперах и время – в секундах.

2)Мощность численно равна работе, совершенной в единицу времени. Следовательно, чтобы найти среднюю мощность электрического тока, надо его работу разделить на время: P = A/t, где P – мощности тока (механическую мощность мы обозначали буквой N).

Работа электрического тока равна произведению напряжения на силу тока и на время: A = UIt, следовательно, P = A/t = UIt/t = UI

Таким образом, мощность электрического тока равна произведению напряжения на силу тока, или P = UI

Из этой формулы можно определить, что U = P/I, I =P/U

За единицу мощности, как известно, принят 1Вт, равный 1 ДЖ/с

Приборы для измерения работы – Электрический счётчик

Источник

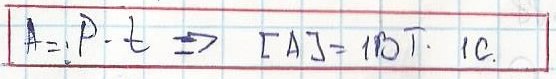
Закон Джоуля-Ленца

На примере многих бытовых приборов понятно, что если через участок цепи проходит электроток и при этом не совершается какая-либо работа, то происходит нагревание проводника. Иногда оно идет на пользу — например, в лампе накаливания или в аппарате дуговой сварки. Но в других случаях тепловой эффект нежелателен — например, перегрев электрической проводки в здании может вызвать пожар. Поэтому в наших интересах управлять таким эффектом, и правило Джоуля-Ленца определяет, от чего зависит тепловое действие тока.

Правило было сформулировано в результате опытов двух ученых — англичанина Джеймса Прескотта Джоуля и российского физика Эмилия Христиановича Ленца. Поскольку ученые работали независимо друг от друга, новый закон назвали двойным именем.

Закон Джоуля-Ленца кратко: нагревание проводника или полупроводника прямо пропорционально его сопротивлению, времени действия тока и квадрату силы тока.

Поскольку сопротивление проводника определяют такие характеристики, как его длина, площадь и проводимость, верны следующие утверждения:

количество теплоты в проводнике снижается при увеличении площади его сечения;

тепловой эффект снижается при уменьшении длины проводника.

Это легко проиллюстрировать, подключив к источнику питания две лампы с разным сопротивлением вначале последовательно, а после — параллельно. При последовательном подключении лампа с большим сопротивлением будет светить ярче, а при параллельном — наоборот.

Природа тепла в проводниках

Разберемся, как происходит нагрев проводника и каким образом этот процесс отвечает формулировке законе Джоуля-Ленца. Как известно, электрический ток представляет собой направленный поток электронов, если речь идет о металлах, и направленный поток ионов — если о растворах электролитов. Проводником называют такой металл, в котором много свободных электронов.

При подключении проводника к сети электроны начинают двигаться в одном направлении под действием электрического поля. При движении они сталкиваются с атомами проводника и передают им свою кинетическую энергию. Чем выше скорость заряженных частиц, тем чаще происходят такие столкновения и больше выделяется кинетической энергии. Часть этой энергии трансформируется в тепло, поэтому проводник нагревается.

Высокая сила тока означает, что через сечение проводника проходит много свободных электронов и столкновения происходят часто. Соответственно, частицам проводника передается много энергии, и он греется сильнее. Именно поэтому в законе Ленца-Джоуля говорится о том, что количество выделяемой теплоты пропорционально квадрату силы тока.

Теперь представим, что сечение проводника увеличилось. Конечно, столкновений частиц будет меньше, а значит — выделится меньше тепла. Вспоминаем, что удельное сопротивление проводника обратно пропорционально его сечению. Чем меньше сечение материала, тем выше его сопротивление и тем сильнее он нагревается. Вот мы и описали тепловое действие тока в соответствии с законом Джоуля-Ленца.

Уравнение Джоуля-Ленца

Посмотрим, как данный закон выражается в математическом виде. Допустим, на некоем участке цепи проходит электрический ток и вызывает нагревание проводника. Если на этом участке нет каких-либо механических процессов или химических реакций, требующих энергозатрат, выделенная проводником теплота Q равна работе тока A.

Q = A

Поскольку А = IUt, где I — сила тока, U — напряжение, а t — время, Q = IUt.

Теперь вспомним, что напряжение можно выразить через сопротивление и силу тока U = IR. Подставим это в формулу:

Q = IUt = I(IR)t = I 2 Rt

Q = I 2 Rt

Мы выразили количество теплоты в проводнике через сопротивление — эта формула для закона Джоуля-Ленца называется интегральной.

Но бывает так, что сила электрического тока неизвестна, зато есть информация о напряжении на участке цепи. В таком случае нужно использовать закон Ома:

I = U/R

Исходя из этого, закон Джоуля-Ленца можно записать в виде дифференциальной формулы:

Напомним, что такое уравнение, как и предыдущее, верно только в том случае, когда вся работа электрического тока уходит на выделение тепла и нет других потребителей энергии.

Итак, у нас есть две формулы для определения количества теплоты, выделяемой проводником при прохождении через него электричества:

При расчетах используют следующие единицы измерения:

количество тепла Q— в джоулях (Дж);

силу тока I — в амперах (А);

сопротивление R — в омах (Ом);

время t — в секундах (с).

Практическое применение

Применение на практике закона Джоуля-Ленца заключается в том, что тепловым действием электрического тока можно управлять, подбирая проводники с нужным сопротивлением. К примеру, для электрических нагревательных приборов, которые должны выделять максимум тепла, выбирают проводники с высоким сопротивлением.

Низкое сопротивление, напротив, позволяет проводнику практически не нагреваться при прохождении тока. Поэтому на промышленных предприятиях с усиленными требованиями к пожаробезопасности для прокладки линий электропередач используется медный кабель. Удельное сопротивление меди сечением 1 мм 2 равно 0,0175 Ом, в то время как у алюминия оно составляет 0,0271 Ом. Медь практически не нагревается, чем снижает риск возгораний.

Примеры задач

Задача 1

Электроплита подключена к сети с напряжением 220 В. Какое количество тепла выделит ее нагревательный элемент за 50 минут, если известно, что сила тока в цепи составляет 10 А.

Решение:

Для того, чтобы рассчитать количество тепла, в данном случае подойдет интегральная формула Джоуля-Ленца Q = I 2 Rt, однако мы не знаем, чему равно сопротивление R. Однако согласно закону Ома R = U/I.

Вычислим сопротивление: R = U/I = 220/10 = 22 Ом.

Подставим имеющиеся данные в формулу:

Q = I 2 Rt = 10 2 × 22 × 3000 = 6 600 000 Дж = 6,6 МДж.

Ответ: плита выделит 6,6 мегаджоулей тепла.

Задача 2

Для обогрева дома требуется, чтобы отопительный прибор выделял 125 кДж тепла в час. Напряжение в электрической сети составляет 220 В. Каким должно быть электрическое сопротивление проводника, чтобы обеспечить данную теплоотдачу?

Решение:

Q = 125 Дж = 125 000 Дж;

В данном случае подойдет уравнение

Ответ: сопротивление проводника 1393,92 Ом.

Источник

Мощность

Определение мощности

Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.

Мощность в физике — это количество работы, которая совершается за единицу времени.

Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.

В электромеханике данная величина тоже связана со скоростью, а конкретно — с тем, как быстро передается ток по участку цепи. Исходя из этого, мы можем рассмотреть еще одно определение.

Мощность — это скалярная физическая величина, которая характеризует скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии.

Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).

Мощность человека в зависимости от деятельности

Вид деятельности

Мощность, Вт

Бег со скоростью 9 км/ч

Плавание со скоростью 50 м/мин

Как обозначается мощность: единицы измерения

В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.

Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.

В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.

Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.

В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.

Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.

Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴

Единицы измерения

1 метрическая лошадиная сила

Все формулы мощности

Зная определения, несложно понять формулы мощности, используемые в разных разделах физики — в механике и электротехнике.

В механике

Механическая мощность (N) равна отношению работы ко времени, за которое она была выполнена.

N = A / t, где A — работа, t — время ее выполнения.

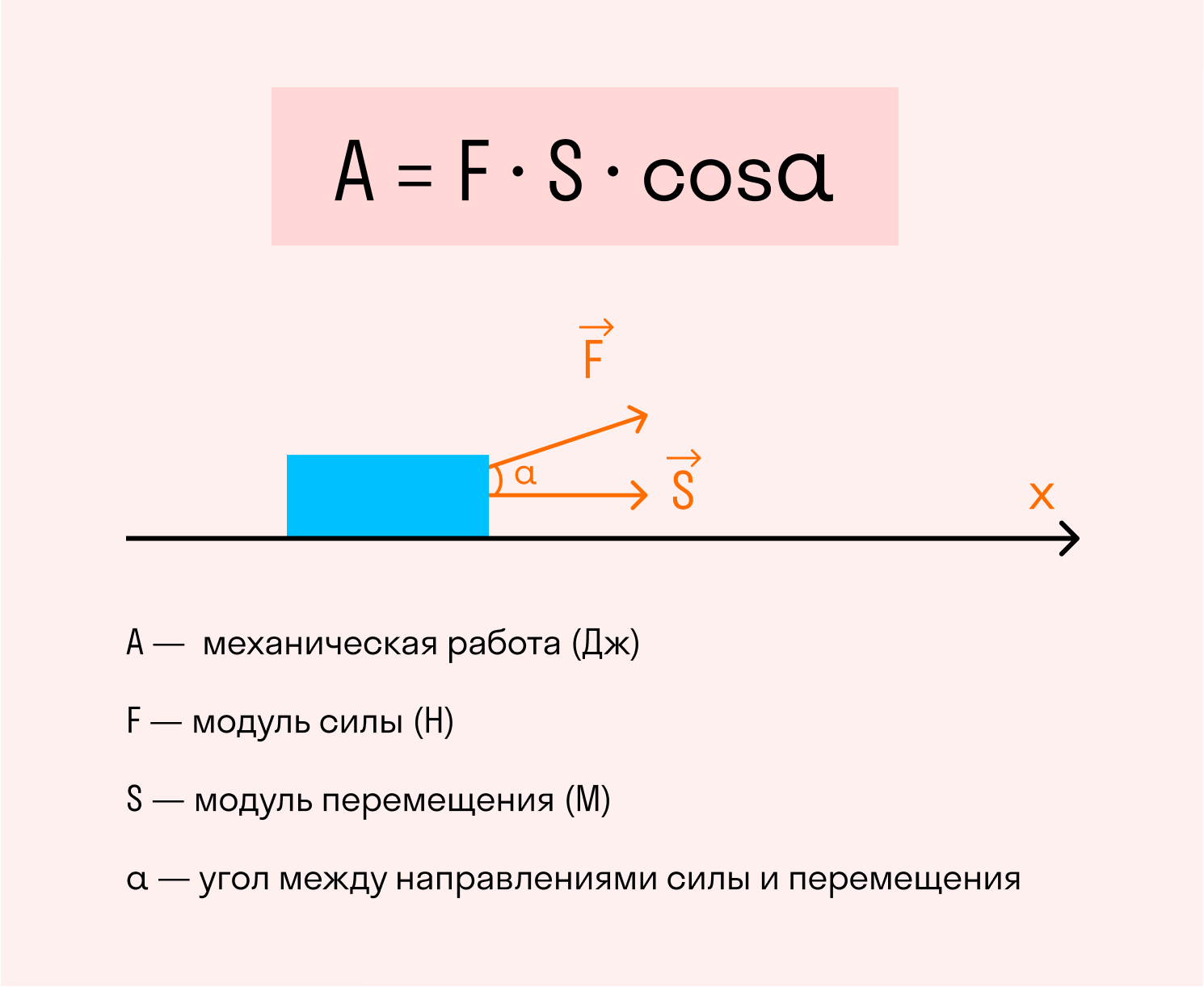
Если вспомнить, что работой называется произведение модуля силы, модуля перемещения и косинуса угла между ними, мы получим формулу измерения работы.

Если направления модуля приложения силы и модуля перемещения объекта совпадают, угол будет равен 0 градусов, а его косинус равен 1. В таком случае формулу можно упростить:

A = F × S

Используем эту формулу для вычисления мощности:

N = A / t = F × S / t = F × V

В последнем выражении мы исходим из того, что скорость (V) равна отношению перемещения объекта на время, за которое это перемещение произошло.

В электротехнике

В общем случае электрическая мощность (P) говорит о скорости передачи энергии. Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.

P = I × U, где I — напряжение, U — сила тока.

В электротехнике существует несколько видов мощности: активная, реактивная, полная, пиковая и т. д. Но это тема отдельного материала, сейчас же мы потренируемся решать задачи на основе общего понимания этой величины. Посмотрим, как найти мощность, используя вышеуказанные формулы по физике.