abs что это в математике
Модуль числа
Определение модуля числа
Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».
Знак модуля: |a| = OA.
Разберем на примере:
Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.
Число 3 (длину отрезка OB) называют модулем числа −3.
Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).
Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.
Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Записывайся на занятия по математике для учеников с 1 по 11 классы.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
3. Модуль отрицательного числа равен противоположному числу.
4. Модуль нуля равен нулю.
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
Оно равно a при а > 0 и −а, при а
Модуль комплексного числа
Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:
Свойства модуля комплексных чисел
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Модуль рационального числа, примеры:
Модуль вещественных чисел
Модуль противоположного числа, нуля, отрицательного и положительного чисел
Закрепим свойства модуля числа, которые мы рассмотрели выше:
Функция ABS excel с примерами
Функция ABS в Excel возвращает абсолютное значение числа. Функция преобразует отрицательные числа в положительные, в то время как положительные числа остаются неизменными.
| Функция ABS на Русском | Функция ABS на Английском |
|---|---|
| ABS | ABS |
Синтаксис
Где число — это числовое значение, для которого нам нужно вычислить абсолютное значение.
Как использовать ABS функцию в Excel?
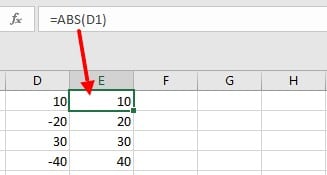
Давайте рассмотрим ряд чисел, чтобы понять, как можно использовать эту функцию.
На скриншоте выше нам дан ряд цифр. Когда мы используем функцию ABS, мы получаем следующие результаты:
Примеры функции ABS в Excel
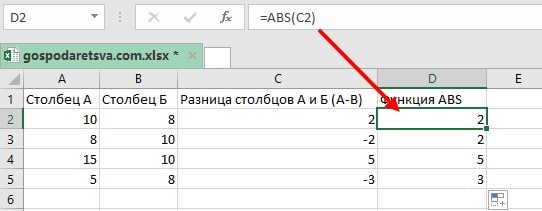
Для нашего анализа нам нужна разница между столбцом A и столбцом B, как указано ниже. В идеале, если вы вычтите столбец A из столбца B, вы можете получить отрицательные числа в зависимости от значений. Однако, если вам нужны абсолютные числа в этом сценарии, мы можем использовать нашу функцию.
Результаты, возвращаемые с помощью функции ABS, будут абсолютными числами. Таким образом, ABS можно комбинировать с другими функциями, такими как SUM, MAX, MIN, AVERAGE и т. Д., чтобы вычислить абсолютное значение для положительных и отрицательных чисел в электронных таблицах Excel.
Давайте посмотрим на несколько примеров того, как ABS можно использовать с другими функциями Excel.
1. SUMIF(СУММЕСЛИ) и ABS
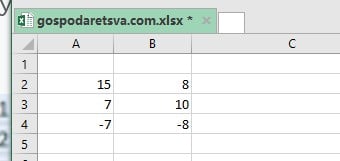
Все мы знаем, что СУММЕСЛИ суммирует значения, если соблюдаются определенные критерии в указанном диапазоне. Предположим, нам даны несколько чисел в столбцах A и B, как показано ниже:
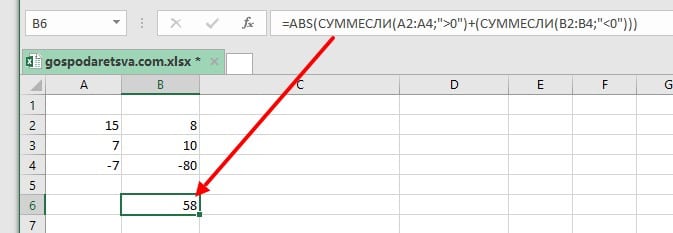
Теперь я хочу вычесть все отрицательные числа в столбце B из всех положительных чисел в столбце A. Я хочу, чтобы результат был абсолютным числом. Поэтому я могу использовать функцию ABS вместе с СУММЕСЛИ следующим образом:
2. Формула SUM и функция ABS
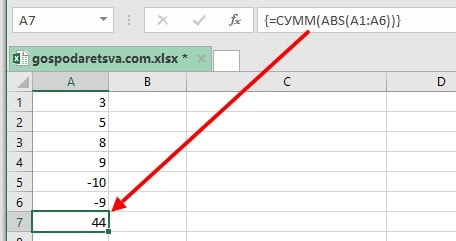
Формулы массива Excel помогают нам выполнять несколько вычислений для заданного массива или столбца значений. Мы можем использовать SUM вместе с ABS, чтобы получить абсолютное значение ряда чисел в столбце или строке. Предположим, нам даны несколько чисел, как показано ниже, поэтому в этом сценарии формула массива SUM для абсолютных значений будет =SUM(ABS(A1:A6)).
Теперь выберите ячейку A7 в своей электронной таблице и введите формулу «=СУММ(ABS(A1:A6))». После ввода формулы в ячейку A7 нажмите «Ctrl + Shift + Enter». Как только мы это сделаем, формула будет заключена в скобки <>, как показано на снимке экрана ниже.
Как видно на скриншоте выше, формула массива также вернула значение 44 в ячейке A7, которое является абсолютным значением данных, введенных в ячейки A1: A6.
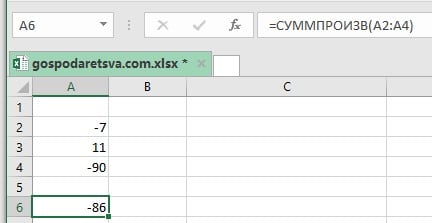
3. СУММПРОИЗВ и ABS
Функция СУММПРОИЗВ позволяет нам включить функцию ABS для получения абсолютных чисел. Предположим, нам даны следующие данные. Если бы мы просто использовали формулу СУММПРОИЗВ, мы получили бы отрицательное число, как показано ниже:
Однако, используя функцию ABS, в результате мы можем получить абсолютное число. Используемая формула будет следующей:
Модуль числа в Python — функции abs() и math.fabs()
З апускаю китайскую реплику «ТАРДИС», и вот мы в пятом классе. На доске нарисована числовая ось, а на ней выделен отрезок. Его начало в точке 4, а конец — в 8. Учительница говорит, что длину отрезка можно найти путём вычитания координаты начала отрезка из координаты его конца. Вычитаем, получаем 4, и радуемся — мы нашли длину. Ура! 🎉
Перемещаемся на год вперёд, и там происходит странное: учительница выделяет мелом другой отрезок, но делает это в каком-то неправильном месте — левее точки с цифрой «0». Теперь перед нами старая задача, но с новыми числами и даже буквами: A, B, минус 4 и минус 8. Мы начинаем искать длину отрезка AB = [-4;-8]:
Переводим непонимающий взгляд с получившейся отрицательной длины на довольную улыбающуюся учительницу, а затем на доску. Там наверху, рядом с сегодняшней датой, написана тема урока: «Модуль числа».
Что такое модуль числа
Модуль числа называют абсолютной величиной.
Для вещественных чисел модуль определяется так:
Т.е. в любом случае, модуль — число большее или равное 0. Поэтому отрицательная длина в примере хитрой учительницы должна была быть взята по модулю:
Тогда дети бы увидели, что геометрический смысл модуля — есть расстояние. Это справедливо и для комплексных чисел, однако формальное определение для них отличается от вещественного:
, где z — комплексное число: z = x + i y.
В то время как math.fabs() может оперировать только вещественными аргументами, abs() отлично справляется и с комплексными. Для начала покажем, что abs в python работает строго в соответствии с математическим определением.
# для вещественных чисел print(abs(-1)) print(abs(0)) print(abs(1)) > 1 > 0 > 1
Как видно, с вещественными числами всё в порядке. Перейдём к комплексным.
# для комплексных чисел print(complex(-3, 4)) print(abs(complex(-3, 4))) > (-3+4j) > 5.0
Если вспомнить, что комплексное число выглядит так: z = x + i y, а его модуль вычисляется по формуле:
Можно заметить, что abs() возвращает значения разных типов. Это зависит от типа аргумента:
print(type(abs(1))) > print(type(abs(1.0))) > print(type(abs(complex(1.0, 1.0))))
print(type(math.fabs(complex(2,3)))) > TypeError: can’t convert complex to float
Для начала работы с fabs() необходимо импортировать модуль math с помощью следующей инструкции:
Мы уже выяснили, что fabs() не работает с комплексными числами, поэтому проверим работу функции на вещественных:
print(math.fabs(-10)) print(math.fabs(0)) print(math.fabs(10)) > 10.0 > 0.0 > 10.0
Функция ABS в Excel
Функция ABS в Excel предназначена для получения модуля числа, то есть его абсолютного значения. В статье приведены примеры использования функции ABS и для чего нужна эта формула на практике, в том числе видеоурок.
Формула ABS очень простая в использовании. Данная функция относится к категории математических и применяется для получения модуля числа.
Модуль числа — абсолютное значение числа без учёта его знака.
Таким образом, функция ABS в Excel возвращает переданный ей числовой аргумент без учёта его знака. Работает это следующим образом:
Итого: на выходе всегда абсолютное значение числа (ABS происходит от absolute), то есть его модуль.
Синтаксис функции ABS
Обобщённый синтаксис функции ABS выглядит следующим образом:
ABS(число), где «число» — это и есть единственный аргумент функции.
Других параметров ABS не принимает (попытка указать два или более аргументов через точку с запятой вызовет ошибку синтаксиса, о чём Excel немедленно Вам сообщит).
Примеры использования функции ABS
После статьи Вы можете скачать файл Excel, в котором приводится несколько практических примеров использования функции ABS для получения модуля чисел. Обратите внимание на то, что при передаче в формулу значения 0, мы получим на выходе тоже ноль.
Примеры использования функции ABS в таблицах Эксель также рассмотрен в небольшом видео-уроке.
Своим опытом использования данной формулы Вы можете поделиться в комментариях после статьи.
Вы можете просмотреть любой прикреплённый документ в виде PDF файла. Все документы открываются во всплывающем окне, поэтому для закрытия документа пожалуйста не используйте кнопку «Назад» браузера.
- Справка по функции ABS в Excel.pdf
Вы можете скачать прикреплённые ниже файлы для ознакомления. Обычно здесь размещаются различные документы, а также другие файлы, имеющие непосредственное отношение к данной публикации.
Примеры функции ABS в Excel для пересчета значения по модулю
Функция ABS находит абсолютное значение числа, переданного в качестве аргумента, и возвращает соответствующее значение.
Примеры использования функции ABS в Excel
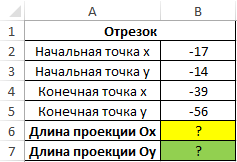
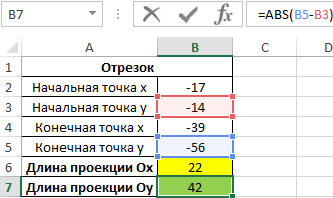
Пример 1. Определить длину проекции отрезка на ось Ox, который задан координатами начальной (-7;-4) и конечной (19;44) точек.
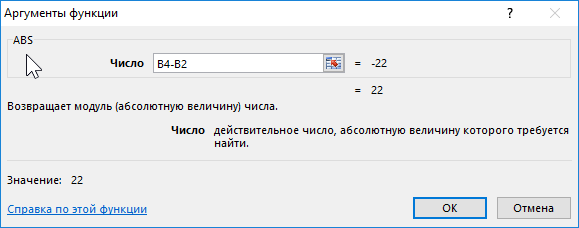
Для определения длины проекции на ось Ox используем следующую формулу:
B4 и B2 – начальная и конечная координаты соответственно. Разность этих координат является искомой длиной проекции. Аналогично найдем величину проекции на ось Oy. Полученные результаты:
В результате вычисления формулы по модулю определилась проекция отрезка на ось Ox.
Расчет разницы между наименьшим отрицательным и положительным числом
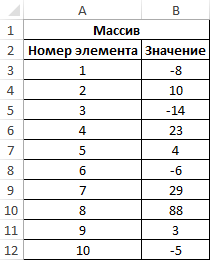
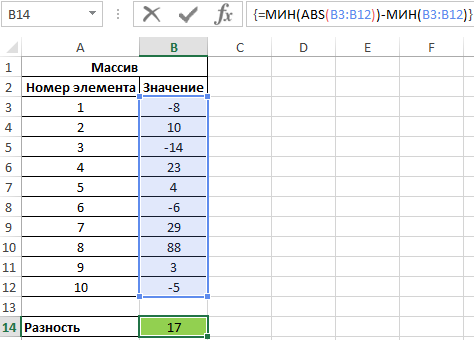
Пример 2. Найти разность между наименьшим и наименьшим абсолютным значениями элементов массива.
Для расчета используем следующую формулу (формула массива CTRL+SHIFT+Enter):
Функция МИН выполняет поиск наименьшего значения в диапазоне. Для поиска наименьшего неотрицательного числа используется выражение МИН(ABS(B3:B12)).
Сумма по модулю в Excel для отрицательных чисел
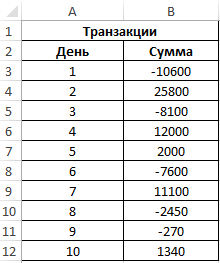
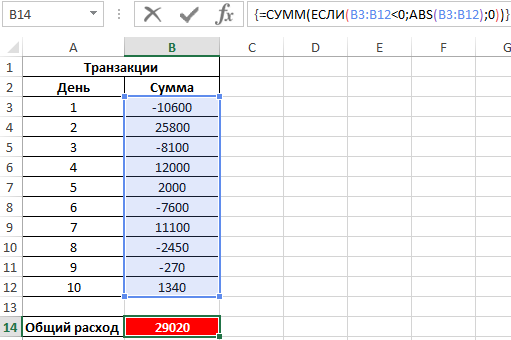
Пример 3. В таблице Excel записаны все транзакции предприятия за определенный промежуток времени. Отрицательные значения соответствуют расходным операциям. Рассчитать сумму расходов за указанный период.
Для расчета используем следующую формулу массива (CTRL+SHIFT+Enter):
То есть, общие расходы предприятия за указанный период составили 29020.
Особенности использования функции ABS в Excel
Функция имеет следующий вариант синтаксической записи:
Единственный аргумент данной функции (является обязательным для заполнения) – число. Он характеризует некоторое вещественное число, у которого будет определено абсолютное значение.