adc snr что это

Раскладываем по полочкам параметры АЦП

Привет, Хабр! Многие разработчики систем довольно часто сталкиваются с обработкой аналоговых сигналов. Не все манипуляции с сигналами можно осуществить в аналоговой форме, поэтому требуется переводить аналог в цифровой мир для дальнейшей постобработки. Возникает вопрос: на какие параметры стоит обратить внимание при выборе микроконтроллера или дискретного АЦП? Что все эти параметры означают? В этой статье постараемся детально рассмотреть основные характеристики АЦП и разобраться на что стоит обратить внимание при выборе преобразователя.

Введение

Рис. 1: Идеальная характеристика АЦП

Статические параметры

Рис. 4: Дифференциальная нелинейность

Рис. 5: Интегральная нелинейность

Динамические параметры

Наглядно данное выражение продемонстрированно на рисунке 7.

Рис. 7: Отношение сигнал/шум

Для оценки SNR АЦП при разработке системы можно воспользоваться следующей формулой:

Первые 2 слагаемых учитывают уровень сигнала и ошибку квантования (нужно понимать, что формула верна для сигнала размаха полной шкалы). Третье слагаемое учитывает эффект передискретизации (выигрыш по обработке или processing gain): если полоса обрабатываемого сигнала (BW Свойство переноса спектра при дискретизации

Рис 12: дискретизация непрерывного сигнала

По фильтрующему свойству дельта-функции:

После дискретизации :

где

С помощью формулы Релея вычислим спектр:

Из этого выражения следует что спектр сигнала будет повторяться во всех зонах Найквиста.

Итак, если есть хороший антиэлайзинговый фильтр, то соблюдая критерий Найквиста, можно оцифровывать сигнал с частотой дискретизации намного ниже полосы АЦП. Но использовать субдискретизацию нужно осторожно. Следует учитывать, что динамические параметры АЦП деградируют (иногда очень сильно) с ростом частоты входного сигнала, поэтому оцифровать сигнал из 6-й зоны так же «чисто», как из 1-й не получится.
Несмотря на это субдискритезация активно используется. Например, для обработки узкополосных сигналов, когда не хочется тратиться на дорогой широкополосный быстродействующий АЦП, который вдобавок имеет высокое потребление. Другой пример – выборка ПЧ (IF-sampling) в РЧ системах. Там благодаря undersampling можно исключить из радиоприемного тракта лишнее аналоговое звено — смеситель (который переносит сигнал на более низкую несущую или на 0).

Сравним архитектуры

На данный момент в мире существует множество различных архитектур АЦП. У каждой из них есть свои преимущества и недостатки. Не существует архитектуры, которая бы достигала максимальных значений всех, описанных выше параметров. Проанализируем какие максимальные параметры скорости и разрешения смогли достичь компании, выпускающие АЦП. Также оценим достоинства и недостатки каждой архитектуры (более подробно о различных архитектурах можно прочитать в статье на хабр).

Тип архитектуры	Преимущества	Недостатки	Максимальное разрешение	Максимальная частота дискретизации
flash	Быстрый преобразователь. Преобразование осуществляется в один такт.	Высокое энергопотребление. Ограниченное разрешение. Требует большой площади кристалла ( компараторов). Трудно согласовать большое количество элементов (как следствие низкий выход годных).	14 бит 128 КВыб/с AD679	3 бит 26 ГВыб/с HMCAD5831
folding-interpolated	Быстрый преобразователь. Преобразование осуществляется в один такт. Требует меньшее число компараторов благодаря предварительной «свёртке» всего диапазона обработки в некоторый более узкий диапазон. Занимает меньше площади.	Ошибки, связанные с нелинейностью блока свёртки. Задержка на установление уровней в блоке свёртки, которая уменьшает максимальную fs. Среднее разрешение.	12 бит 6.4 ГВыб/с ADC12DL3200	12 бит 6.4 ГВыб/с ADC12DL3200
SAR	Высокая точность. Низкое энергопотребление. Легка в использовании.	Ограниченная скорость.	32 бит 1 МВыб/с LTC2500	10 бит 40 МВыб/с XRD64L43
pipeline	Быстрый преобразователь. Самая высокая точность среди быстрых АЦП. Не занимает большую площадь. Имеет меньшее потребления, среди аналогичных быстрых преобразователей.	Конвейерная задержка.	24 бит 192 КВыб/с AK5386	12 бит 10.25 ГВыб/с AD9213
dual-slope	Средняя точность преобразования. Простота конструкции. Низкое потребление. Устойчивость к изменениям факторов внешней среды.	Обрабатывает низкочастотные Сигналы (низкая fs). Посредственное разрешение.	12+знаковый бит 10 Выб/с TC7109	5+знак бит 200 КВыб/с HI3-7159
∑-Δ	Самая высокая точность пре- Образования благодаря эффекту «Noise shaping» (специфическая фильтрация шума квантования) и передискретизации.	Не может работать с широкополосным сигналом.	32 бита 769 КВыб/с AK5554	12 бит 200МВыб/с ADRV9009

Информацию для таблицы брал на сайте arrow, поэтому если что-то упустил поправляйте в комментариях.

Источник

Простой цифровой радиоприёмник. Часть 3.

Продолжаю развивать тему. Сегодня немного отвлечемся от внутренней структуры приемника и поговорим о околожелезячной тематике. А именно о главном элементе цифрового приемника, от которого зависит очень многое – АЦП. Ну и еще про кое-какие фишки. Постараюсь, как могу объяснить все наиболее просто.: о)

Для наших целей применимы, пожалуй, только высокоскоростные конвейерные АЦП, поэтому речь пойдет о них.
На характеристиках по постоянному току и интерфейсах заострять внимание не буду, думаю с этим с легкостью разберется каждый сам.
Для начала определим основные характеристики АЦП по переменному току, которые очень важны как при расчетах, так и при выборе конкретной модели АЦП. Поехали…

SNR – отношение сигнал шум
SINAD – отношение сигнала к шуму и искажениям
ENOB – эффективное число разрядов
SFDR –динамический диапазон свободный от гармоник.

SNR – отношение сигнал шум.

Это отношение СКЗ амплитуды сигнала к среднему значению суммы квадратов всех остальных составляющих спектра за исключением первых 6 (или 5) гармоник сигнала и постоянной составляющей.
У любого АЦП в зависимости от разрядности есть некоторая ошибка квантования (ошибка определения входного значения), которая создает так называемый шум квантования. Т.е. чем меньше разрядность АЦП, тем сильнее он шумит и соответственно меньше SNR. Для любого АЦП справедливо следующее соотношение:

SNR = 6.02*N + 1.76 [дБ] (1)

Где N – число разрядов.
По этой формуле мы можем оценить теоретический SNR, который может быть у АЦП определенной разрядности. Например, для 12 разрядного АЦП, это число будет:

SNR = 6.02 * 12 + 1.76 = 74 дБ.

Шум квантования можно сказать, что распределен равномерно по все зоне Найквиста. Многие задаются вопросом, как может быть SNR радиоприемника или другой системы с цифровым фильтром выше, чем SNR АЦП?
Давайте посмотрим на график:

На рисунке изображено распределение плотности шума квантования АЦП в первой зоне Найквиста. Как я уже сказал выше, плотность шума распределена равномерно по всей зоне, однако полоса пропускания приемника Fпр, значительно меньше всей зоны. Следовательно, в эту зону попадает только часть этого шума. Если вся остальная часть зоны Найквиста будет отфильтрована цифровым фильтром, тогда в формулу расчета SNR системы добавиться так называемый коэффициент обработки или системное усиление.

Кобр = 10 lg (Fсемпл/2*Fпр)

Откуда общий SNR системы будет равен

SNR = 6.02N + 1.76 + Kобр

Давайте теперь прикинем теоретический SNR нашего приемника имеющего 12 разрядный АЦП, 80 мега выборок в секунду, и полосу пропускания 3 кГц.

SNR = 6.02 * 12 + 1.76 + 10 lg (80000000/2*3000) = 115.249 дБ.

Как бы это не казалось странным, но SNR системы при таких условиях соответствует, аж 18 битному АЦП. Понимаю, это вызывает некоторый разрыв шаблона,… но что поделать, такова суровая реальность. Однако, это теоретически максимальное значение, в реальности все получается несколько не так радужно.

SINAD – отношение сигнала к шуму и искажениям

В принципе те же яйца что и SNR, только уже учитываются те самые 6 гармоник, которые мы откинули в определении SNR.

ENOB – эффективное число разрядов

Если в уравнение (1) вместо SNR подставить SINAD и выразить N, то мы получим эффективное число разрядов ENOB.

ENOB = (SINAD – 1.76)/6.02

Дело в том, что младшие биты АЦП из-за его не идеальности представляют собой шум и не несут полезной информации. И как раз значение ENOB говорит нам о том, сколько бит могут нести информацию. По сути, это реальная разрядность АЦП.

Это очень важный параметр, всегда обращайте на него внимание. Зачастую в рекламном листке на АЦП стоит 14 бит, а в реальности эффективная разрядность АЦП может оказаться 12 бит, а то и менее. Старайтесь выбирать АЦП с максимальным ENOB, при прочих равных условиях.
Откуда более правильным, на мой взгляд, при расчете SNR, в формуле (1) использовать не N, а ENOB. Для AD9236 на частоте 40 Мгц ENOB = 11.4, откуда SNR приемника:

SNR = 6.02 * 11.4 + 1.76 + 10 lg (80000000/2*3000) = 111.637 дБ.

Со снижением входной частоты ENOB, конечно же, несколько увеличивается но, как правило, незначительно и этот расчет я считаю более верным. Лучше слегка занизить параметры чем завысить, кто считает иначе?: о).

Еще раз повторюсь это, по сути, идеальный расчет. В реальности есть хренова туча нюансов, например к шуму квантования добавится шум источника питания, шум предварительного усилителя, фазовый шум, да даже высокомные резисторы шумят больше чем низкоомные (не знали? А ведь резисторы обратной связи в ОУ на ВЧ не спроста такие низкие…), кривость разводки платы и т.п…. Нюансов много, а это всего лишь азбука начального уровня.

SFDR – динамический диапазон свободный от гармоник (спур).

Это отношение СКЗ сигнала к СКЗ наихудшей (самой большой по амплитуде) гармоники (спуры) не зависимо от того, где она наложилась или что является ее источником.
SFDR очень важный параметр, позволяющий оценить наименьшее значение сигнала, которое можно отличить от мощной помехи блокирующей прием. Значение SFDR может указываться как относительно полной шкалы (dBSF), так и относительно амплитуды сигнала (dBc). Чем больше это число, тем соответственно лучше.
Выглядеть все эти чудеса могут как – то так

В зависимости от входной частоты сигнала, SFDR, конечно же, меняется. И как правило при повышении частоты SFDR снижается из-за нелинейностей и прочих искажений которые вносит сама АЦП. Все это обычно указано в даташите в виде графиков и при проектировании системы смотрите, где вы собираетесь работать и какие характеристики АЦП в этой зоне.

Я рассмотрел только часть характеристик по переменному току (которые я считаю минимальным джентльменским набором), есть еще интермодуляционные искажения IMD, дифференциальные нелинейные искажения DNL, общие нелинейные искажения THD, интермодуляционные искажения второго и третьего порядка IMD2, IMD3. И изучение этих характеристик я вам оставлю на домашнее задание: о).

Это страшное слово Джиттер

У любого тактового сигнала, есть такое нехорошее свойство как фазовая не стабильность фронтов — JITTER. Из-за чего, от выборки к выборке в коде АЦП появляется некоторая погрешность, обусловленная изменением фронта синхронизации.

Эта ошибка накапливается и создает так называемый фазовый шум, который добавляется к общему шуму системы, снижая её SNR. Уровень фазового шума тем больше, чем выше скорость нарастания входного сигнала АЦП, т.е. чем выше частота. Следовательно, при высоких входных частотах требования к тактовому генератору становятся все выше.

Например, вот так выглядит график снижения SNR зависящий от величины джиттера для АЦП AD9236.

Для оценки SNR обусловленного только величиной джиттера (для идеального АЦП), существует следующее соотношение:

SNRj = 20lg(1/ (2 * пи * f * tj))

Где, f – частота входного сигнала, tj – величина джиттера

Исходя из этого соотношения, можно прикинуть какой генератор нам нужен для конкретных задач.
Чтобы сохранить SNR АЦП на должном уровне, расчетный SNRj по джиттеру должен быть больше SNR АЦП. В этом случае обеспечивается условие, когда уровень фазового шума меньше шума квантования АЦП.

В принципе, для нашего КВ приемника с некоторым снижением характеристик на ВЧ, можно применить генератор с величиной джиттера не более 1 пикосекунды. Такие генераторы относительно дешевы и стоят, как правило, не более 300р. Чего не скажешь о более крутых генераторах, цена которых может превышать стоимость самой АЦП. Поэтому к выбору генератора стоит подходить со всей серьезностью и не брать абы какой…

Если в системе планируется применить драйвера тактирования, то соответственно к величине джиттера генератора добавляется джиттер драйверов. Про это не нужно забывать.

Однако, это не относится к драйверам тактирования (ADF4001) с системой ФАПЧ, которые позволяют из шумящего генератора сделать менее шумящий. Т.е. понизить величину джиттера.

Дизеринг

Фишка довольно известная, но все же расскажу пару слов о ней. Те более в моем макете дизеринг предусмотрен, кто изучал схему думаю обратили внимание на ФНЧ идущие от ПЛИС к входу предварительного усилителя.
Дизеринг – это подмешивание псевдослучайного шума на вход АЦП, данный метод позволяет повысить точность системы, снизить влияние нелинейностей АЦП.

Представим, что наш 12 разрядный АЦП является идеальным и не шумящим. Полная шкала у него пусть будет 4096 мВ. Если мы на вход этого АЦП подадим постоянное напряжение, то измерять мы его сможем с точностью 1 мВ или +-0.5мВ.

Давайте добавим на вход нашего АЦП совместно с постоянным напряжением 1000 мВ немного шума, амплитудой около 0.5 – 1.5 младшего разряда. В результате на выходе АЦП мы сможем наблюдать код 1000, а так же 1001, 999, чуть реже 998, 1002 и т.д. Теперь давайте вычислим среднее значение, допустим 100 отсчетов, результат нам даст напряжение с точностью примерно в 10 раз выше или около 0.1мВ. Т.е. корень из 100.

Далее если АЦП идеален и шум правильный, как по распределению, так и по амплитуде увеличивая количество суммируемых отсчетов и вычисляя среднее значение можно увеличивать точность измерения, теоретически практически предела нет…

Но как обычно бывает, “хрустальные мечты разбиваются о чугунную Ж реальности”(с). Шум который мы подмешиваем на самом деле мешает, он снижает SNR нашего АЦП, и появляется на выходе системы, что разумеется очень не приятно. Для того чтобы снизить пролезание шума на выход применяют шум по возможности небольшой амплитуды и со спектром за пределами интересующей области частот.

Нелинейности АЦП можно снизить таким же образом, но уже с гораздо большой амплитудой внеполосного шума. Т.е. мы можем в какой-то мере увеличить SFDR АЦП.

В современных АЦП дизеринг уже встроен в сам чип, и достаточно дрыгунть ногой и вот оно, наше счастье…: о)

Завербуем на службу алиасинг.

Бытует мнение, что алиасинг (наложение спектра) зло. Но это верно только от части, в радиосвязи эта штука весьма полезна и позволяет обойтись без всяких там дополнительных смесителей, перенося более высокочастотные сигналы в первую зону Найквиста. Откуда дает возможность применять менее скоростные, более дешевые АЦП, но при этом работать с УКВ.

Давайте посмотрим, как нашим КВ приемником с частотой дискретизации 80МГц мы смогли бы принимать УКВ, например в обычном вещательном диапазоне, на частоте 100 МГц. Сигнал с частотой 100 МГц находится в 3 зоне Найквиста и он субдискретизирован. Поэтому он переносится в первую зону, однако так как ширина полосы сигнала на частоте 100 Мгц значительно меньше (допустим для FM полоса 30 КГц), чем Fs/2 то сигнал остается передескритизирован и появится на частоте 20 Мгц (100МГц – 80МГц) без потери информации.

Для нормальной работы этого метода, потребуется с помощью полосового фильтра обрезать все зоны Найквиста кроме третьей. Вот таким не хитрым образом мы можем слушать УКВ. К сожалению характеристики АЦП на более высоких частотах снижаются, а требования к тактовому генератору увеличиваются. Но я думаю теперь вы уже сами можете прикинуть на сколько снизятся SNR и SFDR нашего АЦП при работе с УКВ…

Для определения в каких высших зонах Найквиста с конкретной моделью АЦП мы можем работать, в даташите обычно указывается максимальная полоса пропускания АЦП.

Ну и хватит думаю на этот раз…
Спасибо за внимание!

Для общего развития:

Комментарии ( 33 )

подскажте как сделать цифровую фильрацию на основе БПФ — секционная свертка по методу перекрытие с накоплением. Делаю как в учебнике — беру блок дополняю нулями в 2 раза больше, режу то что не нужно — ОБПФ — пол результата с сумой прошлой половины на выход, а вторую половину — для сумирования с следующим. НО — всплески на краях выходных блоков присутствуют…

Источник

Аналого-цифровое преобразование для начинающих

В этой статье рассмотрены основные вопросы, касающиеся принципа действия АЦП различных типов. При этом некоторые важные теоретические выкладки, касающиеся математического описания аналого-цифрового преобразования остались за рамками статьи, но приведены ссылки, по которым заинтересованный читатель сможет найти более глубокое рассмотрение теоретических аспектов работы АЦП. Таким образом, статья касается в большей степени понимания общих принципов функционирования АЦП, чем теоретического анализа их работы.

«

В качестве отправной точки дадим определение аналого-цифровому преобразованию. Аналого-цифровое преобразование – это процесс преобразования входной физической величины в ее числовое представление. Аналого-цифровой преобразователь – устройство, выполняющее такое преобразование. Формально, входной величиной АЦП может быть любая физическая величина – напряжение, ток, сопротивление, емкость, частота следования импульсов, угол поворота вала и т.п. Однако, для определенности, в дальнейшем под АЦП мы будем понимать исключительно преобразователи напряжение-код.

Понятие аналого-цифрового преобразования тесно связано с понятием измерения. Под измерением понимается процесс сравнения измеряемой величины с некоторым эталоном, при аналого-цифровом преобразовании происходит сравнение входной величины с некоторой опорной величиной (как правило, с опорным напряжением). Таким образом, аналого-цифровое преобразование может рассматриваться как измерение значения входного сигнала, и к нему применимы все понятия метрологии, такие, как погрешности измерения.

Основные характеристики АЦП

АЦП имеет множество характеристик, из которых основными можно назвать частоту преобразования и разрядность. Частота преобразования обычно выражается в отсчетах в секунду (samples per second, SPS), разрядность – в битах. Современные АЦП могут иметь разрядность до 24 бит и скорость преобразования до единиц GSPS (конечно, не одновременно). Чем выше скорость и разрядность, тем труднее получить требуемые характеристики, тем дороже и сложнее преобразователь. Скорость преобразования и разрядность связаны друг с другом определенным образом, и мы можем повысить эффективную разрядность преобразования, пожертвовав скоростью.

Существует множество типов АЦП, однако в рамках данной статьи мы ограничимся рассмотрением только следующих типов:

Наибольшим быстродействием и самой низкой разрядностью обладают АЦП прямого (параллельного) преобразования. Например, АЦП параллельного преобразования TLC5540 фирмы Texas Instruments обладает быстродействием 40MSPS при разрядности всего 8 бит. АЦП данного типа могут иметь скорость преобразования до 1 GSPS. Здесь можно отметить, что еще большим быстродействием обладают конвейерные АЦП (pipelined ADC), однако они являются комбинацией нескольких АЦП с меньшим быстродействием и их рассмотрение выходит за рамки данной статьи.

Среднюю нишу в ряду разрядность-скорость занимают АЦП последовательного приближения. Типичными значениями является разрядность 12-18 бит при частоте преобразования 100KSPS-1MSPS.

Наибольшей точности достигают сигма-дельта АЦП, имеющие разрядность до 24 бит включительно и скорость от единиц SPS до единиц KSPS.

Еще одним типом АЦП, который находил применение в недавнем прошлом, является интегрирующий АЦП. Интегрирующие АЦП в настоящее время практически полностью вытеснены другими типами АЦП, но могут встретиться в старых измерительных приборах.

АЦП прямого преобразования

АЦП прямого преобразования получили широкое распространение в 1960-1970 годах, и стали производиться в виде интегральных схем в 1980-х. Они часто используются в составе «конвейерных» АЦП (в данной статье не рассматриваются), и имеют разрядность 6-8 бит при скорости до 1 GSPS.

Архитектура АЦП прямого преобразования изображена на рис. 1

Рис. 1. Структурная схема АЦП прямого преобразования

Принцип действия АЦП предельно прост: входной сигнал поступает одновременно на все «плюсовые» входы компараторов, а на «минусовые» подается ряд напряжений, получаемых из опорного путем деления резисторами R. Для схемы на рис. 1 этот ряд будет таким: (1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16) Uref, где Uref – опорное напряжение АЦП.

Пусть на вход АЦП подается напряжение, равное 1/2 Uref. Тогда сработают первые 4 компаратора (если считать снизу), и на их выходах появятся логические единицы. Приоритетный шифратор (priority encoder) сформирует из «столбца» единиц двоичный код, который фиксируется выходным регистром.

Теперь становятся понятны достоинства и недостатки такого преобразователя. Все компараторы работают параллельно, время задержки схемы равно времени задержки в одном компараторе плюс время задержки в шифраторе. Компаратор и шифратор можно сделать очень быстрыми, в итоге вся схема имеет очень высокое быстродействие.

Но для получения N разрядов нужно 2^N компараторов (и сложность шифратора тоже растет как 2^N). Схема на рис. 1. содержит 8 компараторов и имеет 3 разряда, для получения 8 разрядов нужно уже 256 компараторов, для 10 разрядов – 1024 компаратора, для 24-битного АЦП их понадобилось бы свыше 16 млн. Однако таких высот техника еще не достигла.

АЦП последовательного приближения

АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь. Подробнее о задаче Фибоначчи можно прочитать, например, здесь: http://www.goldenmuseum.com/2015AMT_rus.html.

Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины входного напряжения с рядом величин, генерируемых следующим образом:

1. на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref).

2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref).

3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата.

Рис. 2. Структурная схема АЦП последовательного приближения.

Таким образом, АЦП последовательного приближения состоит из следующих узлов:

1. Компаратор. Он сравнивает входную величину и текущее значение «весового» напряжения (на рис. 2. обозначен треугольником).

2. Цифро-аналоговый преобразователь (Digital to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода.

3. Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП.

4. Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства.

Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767).

И, наконец, самый интересный тип АЦП – сигма-дельта АЦП, иногда называемый в литературе АЦП с балансировкой заряда. Структурная схема сигма-дельта АЦП приведена на рис. 3.

Рис.3. Структурная схема сигма-дельта АЦП.

Принцип действия данного АЦП несколько более сложен, чем у других типов АЦП. Его суть в том, что входное напряжение сравнивается со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжение (рис. 4). Результатом работы данной схемы является поток нулей и единиц на выходе компаратора, который затем пропускается через цифровой ФНЧ, в результате получается N-битный результат. ФНЧ на рис. 3. Объединен с «дециматором», устройством, снижающим частоту следования отсчетов путем их «прореживания».

Рис. 4. Сигма-дельта АЦП как следящая система

Ради строгости изложения, нужно сказать, что на рис. 3 изображена структурная схема сигма-дельта АЦП первого порядка. Сигма-дельта АЦП второго порядка имеет два интегратора и две петли обратной связи, но здесь рассматриваться не будет. Интересующиеся данной темой могут обратиться к [3].

На рис. 5 показаны сигналы в АЦП при нулевом уровне на входе (сверху) и при уровне Vref/2 (снизу).

Рис. 5. Сигналы в АЦП при разных уровнях сигнала на входе.

Более наглядно работу сигма-дельта АЦП демонстрирует небольшая программа, находящаяся тут: http://designtools.analog.com/dt/sdtutorial/sdtutorial.html.

Теперь, не углубляясь в сложный математический анализ, попробуем понять, почему сигма-дельта АЦП обладают очень низким уровнем собственных шумов.

Рассмотрим структурную схему сигма-дельта модулятора, изображенную на рис. 3, и представим ее в таком виде (рис. 6):

Рис. 6. Структурная схема сигма-дельта модулятора

Здесь компаратор представлен как сумматор, который суммирует непрерывный полезный сигнал и шум квантования.

Пусть интегратор имеет передаточную функцию 1/s. Тогда, представив полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:

То есть, фактически сигма-дельта модулятор является фильтром низких частот (1/(s+1)) для полезного сигнала, и фильтром высоких частот (s/(s+1)) для шума, причем оба фильтра имеют одинаковую частоту среза. Шум, сосредоточенный в высокочастотной области спектра, легко удаляется цифровым ФНЧ, который стоит после модулятора.

Рис. 7. Явление «вытеснения» шума в высокочастотную часть спектра

Однако следует понимать, что это чрезвычайно упрощенное объяснение явления вытеснения шума (noise shaping) в сигма-дельта АЦП.

Итак, основным достоинством сигма-дельта АЦП является высокая точность, обусловленная крайне низким уровнем собственного шума. Однако для достижения высокой точности нужно, чтобы частота среза цифрового фильтра была как можно ниже, во много раз меньше частоты работы сигма-дельта модулятора. Поэтому сигма-дельта АЦП имеют низкую скорость преобразования.

Они могут использоваться в аудиотехнике, однако основное применение находят в промышленной автоматике для преобразования сигналов датчиков, в измерительных приборах, и в других приложениях, где требуется высокая точность. но не требуется высокой скорости.

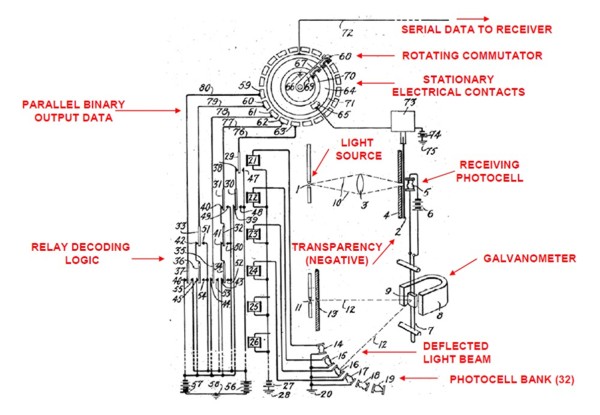
Самым старым упоминанием АЦП в истории является, вероятно, патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Изображенное в патенте устройство фактически является 5-битным АЦП прямого преобразования.

Рис. 8. Первый патент на АЦП

Рис. 9. АЦП прямого преобразования (1975 г.)

Устройство, изображенное на рисунке, представляет собой АЦП прямого преобразования MOD-4100 производства Computer Labs, 1975 года выпуска, собранный на основе дискретных компараторов. Компараторов 16 штук (они расположены полукругом, для того, чтобы уравнять задержку распространения сигнала до каждого компаратора), следовательно, АЦП имеет разрядность всего 4 бита. Скорость преобразования 100 MSPS, потребляемая мощность 14 ватт.

На следующем рисунке изображена продвинутая версия АЦП прямого преобразования.

Рис. 10. АЦП прямого преобразования (1970 г.)

Устройство VHS-630 1970 года выпуска, произведенное фирмой Computer Labs, содержало 64 компаратора, имело разрядность 6 бит, скорость 30MSPS и потребляло 100 ватт (версия 1975 года VHS-675 имела скорость 75 MSPS и потребление 130 ватт).

Источник