алгоритм машинного обучения это

Machine Learning – не только нейронки

Нейронные сети и глубокое обучение (deep learning) у всех на слуху, но нейросети – это лишь подобласть такого обширного предмета, как машинное обучение (machine learning). Существует несколько сотен других алгоритмов, которые способны быстро и эффективно решать задачи искусственного интеллекта и в большинстве случаев являются более интерпретируемыми для человека. В этой статье рассмотрим алгоритмы классического машинного обучения, принцип работы нейросетей, подготовку данных для обучения моделей и задачи, которые решают с помощью искусственного интеллекта.

Основные задачи машинного обучения

Восстановление регрессии (прогнозирования) – построение модели, способной предсказывать численную величину на основе набора признаков объекта.

Классификация – определение категории объекта на основе его признаков.

Кластеризация – распределение объектов.

Допустим, есть набор данных со статистикой по приложениям. В нем есть следующие сведения: размер, категория, количество скачиваний, количество отзывов, рейтинг, возрастной рейтинг, жанр и цена. С помощью этого набора данных и машинного обучения можно решить такие задачи:

Прогнозирование рейтинга приложения на основе признаков: размер, категория, возрастной рейтинг, жанр и цена – задача регрессии.

Определение категории приложения на основе набора признаков: размер, возрастной рейтинг, жанр и цена – задача классификации.

Разбиение приложений на группы на основании множества признаков (например, количество отзывов, скачиваний, рейтинга) таким образом, чтобы приложения внутри группы были более похожи друг на друга, чем приложения разных групп.

Нейронные сети (многослойный перцептрон)

Существует мнение, что лучшие идеи для изобретений человек заимствует у природы. Нейронные сети – это именно тот случай, ведь сама концепция нейросетей базируется на функциональных особенностях головного мозга.

Принцип работы

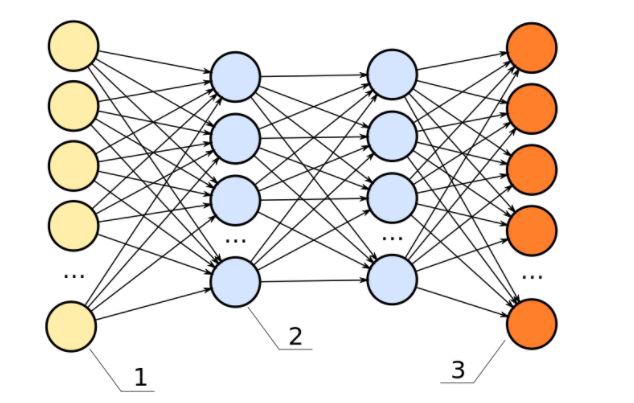
Есть определенное количество нейронов, которые между собой связаны и взаимодействуют друг с другом путем передачи сигналов. Также есть рецепторы, которые получают информацию, поступающую извне, и исполнительный орган, на который приходит итоговый сигнал. По схожему принципу работают искусственные нейросети: есть несколько слоев с нейронами и связи между ними (каждая связь имеет свой весовой коэффициент). По связям передаются сигналы в виде численных значений, первый слой выполняет собой роль рецепторов, то есть получает набор признаков для обучения, и есть выходной слой, который выдает ответ.

Нейронные связи в головном мозге («Создаем нейронную сеть», Тарик Рашид) Пример искусственной трехслойной нейросети («Создаем нейронную сеть», Тарик Рашид)

Каждый слой нейросети оперирует разными представлениями о данных. На рисунке ниже можно увидеть пример использованиям глубокого обучения (нейросети) для распознавания образа на картинке. На входной слой нам поступают пиксели изображений, далее после вычислений между входным и первым скрытым слоем мы получаем границы, на втором скрытом слое – контуры, на третьем – части объектов, на выходном – вероятности принадлежности изображения к каждому типу объектов.

Пример использования нейросети для распознавания образа ( «Глубокое обучение», Ян Гудфеллоу)

Как настраивать

Настраивается путем задания количества узлов, скрытых слоев и выбора функции активации. В искусственных нейронных сетях функция активации нейрона отвечает за выходной сигнал, который определяется входным сигналом или набором входных сигналов.

Задачи: классификация, регрессия, кластеризация.

Классические алгоритмы машинного обучения

K-ближайших соседей

Метод K-ближайших соседей – простой и эффективный алгоритм, его можно описать известной поговоркой: “Скажи мне, кто твой друг, и я скажу, кто ты”.

Принцип работы

Пусть имеется набор данных с заданными классами. Мы можем определить класс неизвестного объекта, если рассмотрим определенное количество ближайших объектов (k) и присвоим тот класс, который имеет большинство “соседей”. Посмотрим на рисунок ниже.

Есть набор точек с двумя классами: синие крестики и красные кружки. Мы хотим определить, к какому классу относится неизвестная зеленая точка. Для этого мы берем k ближайших соседей, в данном случае 3, и смотрим, к каким классам они относятся. Из трех ближайших соседей больше оказалось синих крестиков, соответственно, мы можем предположить, что зеленая точка также, скорее всего, относится к этому классу.

Как настраивать

Необходимо подобрать параметр k (количество ближайших соседей) и метрику для измерения расстояний между объектами.

Задачи: классификация, также может применяться и для задач регрессии.

Линейная регрессия

Линейная регрессия – простая и эффективная модель машинного обучения, способная решать задачи быстро и недорого.

Принцип работы

Модель линейной регрессии можно описать уравнением

Здесь x – это значения признаков, y – целевая переменная, a – весовые коэффициенты признаков. При обучении модели весовые коэффициенты подбираются таким образом, чтобы как можно лучше описывалась линейная зависимость признаков от целевой переменной.

Пример: задача предсказания стоимости квартиры в зависимости от площади и удаленности от метро в минутах. Целевой переменной (y) будет являться стоимость, а признаками (x) – площадь и удаленность.

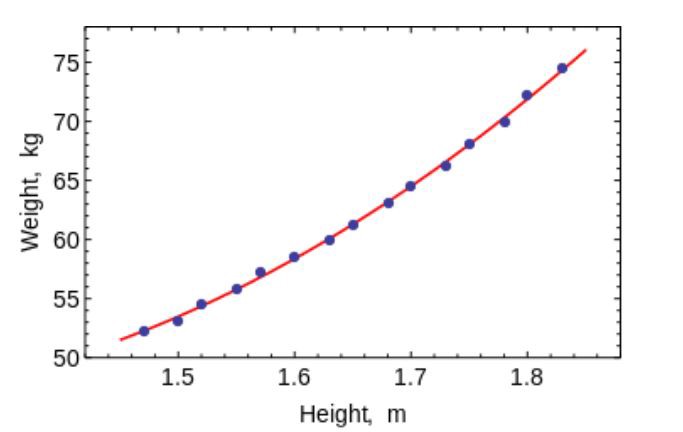
На рисунке ниже также представлен пример построения линейной регрессии. Красная прямая более точно описывает линейную зависимость x от y.

Как настраивать

Для многих моделей Machine Learning, в частности и для линейной регрессии, можно улучшить итоговое качество с помощью регуляризации.

Регуляризация в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить некорректно поставленную задачу или предотвратить переобучение, то есть ситуацию, когда модель хорошо показывает себя на тренировочный данных, но перестаёт работать на новых.

Распространенные методы регуляризации для повышения качества модели линейной регрессии:

Ridge — один из методов понижения размерности. Применяется для борьбы с переизбыточностью данных, когда независимые переменные коррелируют друг с другом (мультиколлинеарность), вследствие чего проявляется неустойчивость оценок коэффициентов линейной регрессии.

LASSO — также как и Ridge, применяется для борьбы с переизбыточностью данных.

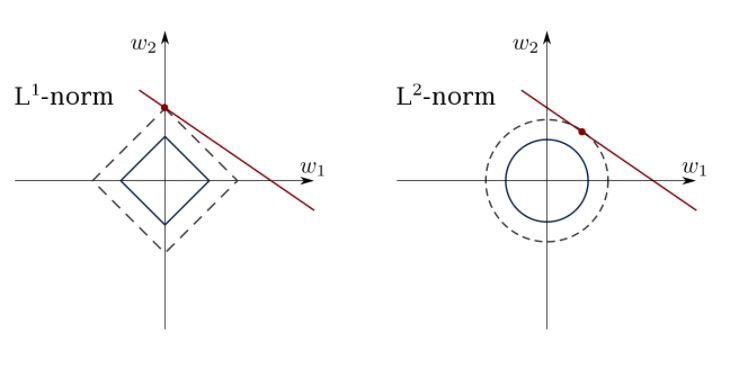
Elastic-Net — модель регрессии с двумя регуляризаторами L1, L2. Частными случаями являются модели LASSO L1 = 0 и Ridge регрессии L2 = 0.

Задачи: регрессия.

Логистическая регрессия

Логистическая регрессия – также простая и эффективная модель машинного обучения, способная решать задачи быстро и недорого.

Принцип работы

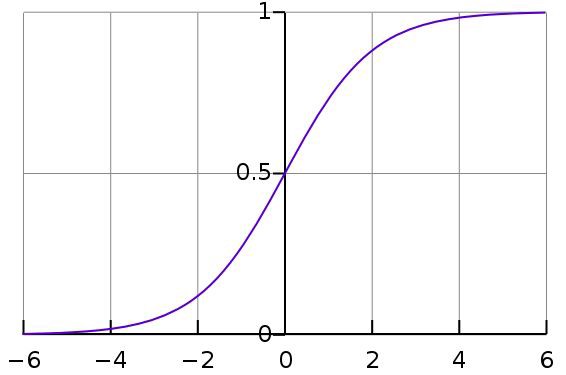
Указанная выше сумма проходит через функцию сигмоиды, которая возвращает число от 0 до 1, характеризующее вероятность отнесения объекта к классу 1. Пример: логистическую регрессию часто применяют в задачах кредитного скоринга, когда по определенным данным о клиенте нужно определить, стоит ли выдавать ему кредит.

Иллюстрация алгоритмов линейной и логистической регрессии (источник)

Как настраивать

Задачи: классификация.

Метод опорных векторов (SVM)

Принцип работы

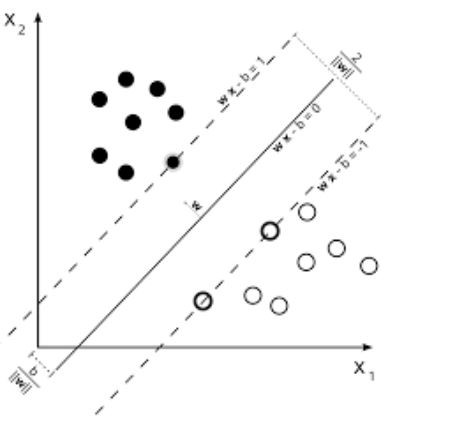
Чтобы лучше всего понять алгоритм метода опорных векторов, рассмотрим рисунок. На рисунке приведен пример двух линейно разделимых классов в двумерном пространстве. Идея алгоритма заключается в нахождении оптимальной разделяющей прямой (или гиперплоскости для более высоких пространств) для отделения объектов одного класса от другого. Пунктирные линии выделяют разделяющую полосу и проводятся через объекты, которые называют опорными. Чем шире разделяющая полоса, тем качественнее модель SVM. Чтобы определить класс объекта, достаточно определить, с какой стороны гиперплоскости он находится.

Как настраивать

Необходимо подобрать оптимальное ядро (функцию переводящую признаковое пространство в более высокую размерность), если линейная зависимость слабо выражена.

Задачи: классификация и регрессия.

Сравнение классических алгоритмов с нейросетью

Для примера мы взяли датасет со статистикой приложений в Play Market. Датасет содержит следующие данные: размер приложения, возрастной рейтинг, количество скачиваний, жанр, категория и др. На данном датасете были обучены модели: линейная регрессия, метод опорных векторов, нейронная сеть (многослойный перцептрон).

В ходе экспериментов были подобраны следующие параметры для моделей машинного обучения:

Линейная регрессия – модели линейной регрессии с регуляризацией не показали результат, превосходящий качество классической линейной регрессии.

Метод опорных векторов – модель метода опорных векторов с RBF-ядром показала лучший результат по сравнению с другими ядрами.

Многослойный перцептрон – оптимальный результат показала модель с 4 слоями, 300 нейронами и функций активацией ReLu. При попытках увеличить количество слоев и нейронов прирост качества не наблюдался.

Решена задача прогнозирования потенциального рейтинга приложения в зависимости от его признаков.

Результаты ошибки среднего отклонения от истинного значения целевой переменной в процентах для каждой модели:

Линейная регрессия – 6.13 %

Метод опорных векторов – 6.01%

Нейронная сеть – 6.41%

Таким образом, классические алгоритмы машинного обучения и нейросети показали приблизительно одинаковое качество. Это связано с тем, что нейросети хорошо обучаются на датасетах с большим размером и обычно применяются для решения задач, где зависимость в данных очень сложна. Поэтому для решения данной задачи можно обойтись применением классических алгоритмов и не прибегать к использованию нейросетей.

На гистограмме ниже представлены итоговые весовые коэффициенты a, полученные при обучении модели линейной регрессии. Чем больше столбик, тем выше влияние признака на целевую переменную. Если столбик направлен вверх, то он оказывает положительное влияние на рост целевой переменной, если вниз – то отрицательное. Другими словами, если приложение имеет жанр “Other” или “Tools”, то, скорее всего, его рейтинг будет высоким, а если у него категория “FAMILY” или “GAME” – то, вероятно, низким. Данная интерпретация весовых коэффициентов линейной регрессии бывает очень полезной при анализе данных.

Гистограмма значений коэффициентов линейной регрессии

Больше наших статей по машинному обучению и обработке изображений:

Источник

Must-have алгоритмы машинного обучения

Этот пост — краткий обзор общих алгоритмов машинного обучения. К каждому прилагается краткое описание, гайды и полезные ссылки.

Метод главных компонент (PCA)/SVD

Это один из основных алгоритмов машинного обучения. Позволяет уменьшить размерность данных, потеряв наименьшее количество информации. Применяется во многих областях, таких как распознавание объектов, компьютерное зрение, сжатие данных и т. п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных или к сингулярному разложению матрицы данных.

SVD — это способ вычисления упорядоченных компонентов.

Метод наименьших квадратов

Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, а также для аппроксимации точечных значений некоторой функции.

Используйте этот алгоритм, чтобы соответствовать простым кривым/регрессии.

Ограниченная линейная регрессия

Метод наименьших квадратов может смутить выбросами, ложными полями и т. д. Нужны ограничения, чтобы уменьшить дисперсию линии, которую мы помещаем в набор данных. Правильное решение состоит в том, чтобы соответствовать модели линейной регрессии, которая гарантирует, что веса не будут вести себя “плохо”. Модели могут иметь норму L1 (LASSO) или L2 (Ridge Regression) или обе (elastic regression).

Используйте этот алгоритм для соответствия линиям регрессии с ограничениями, избегая переопределения.

Метод k-средних

Всеми любимый неконтролируемый алгоритм кластеризации. Учитывая набор данных в виде векторов, мы можем создавать кластеры точек на основе расстояний между ними. Это один из алгоритмов машинного обучения, который последовательно перемещает центры кластеров, а затем группирует точки с каждым центром кластера. Входные данные – количество кластеров, которые должны быть созданы, и количество итераций.

Логистическая регрессия

Логистическая регрессия ограничена линейной регрессией с нелинейностью (в основном используется сигмоидальная функция или tanh) после применения весов, следовательно, ограничение выходов приближено к + / — классам (что равно 1 и 0 в случае сигмоида). Функции кросс-энтропийной потери оптимизированы с использованием метода градиентного спуска.

Примечание для начинающих: логистическая регрессия используется для классификации, а не регрессии. В целом, она схожа с однослойной нейронной сетью. Обучается с использованием методов оптимизации, таких как градиентный спуск или L-BFGS. NLP-разработчики часто используют её, называя “классификацией методом максимальной энтропии”.

Используйте LR для обучения простых, но очень “крепких” классификаторов.

SVM (Метод опорных векторов)

SVM – линейная модель, такая как линейная/логистическая регрессия. Разница в том, что она имеет margin-based функцию потерь. Вы можете оптимизировать функцию потерь, используя методы оптимизации, например, L-BFGS или SGD.

Одна уникальная вещь, которую могут выполнять SVM – это изучение классификаторов классов.

SVM может использоваться для обучения классификаторов (даже регрессоров).

Нейронные сети прямого распространения

В основном, это многоуровневые классификаторы логистической регрессии. Многие слои весов разделены нелинейностями (sigmoid, tanh, relu + softmax и cool new selu). Также они называются многослойными перцептронами. FFNN могут быть использованы для классификации и “обучения без учителя” в качестве автоэнкодеров.

FFNN можно использовать для обучения классификатора или извлечения функций в качестве автоэнкодеров.

Свёрточные нейронные сети

Практически все современные достижения в области машинного обучения были достигнуты с помощью свёрточных нейронных сетей. Они используются для классификации изображений, обнаружения объектов или даже сегментации изображений. Изобретенные Яном Лекуном в начале 90-х годов, сети имеют сверточные слои, которые действуют как иерархические экстракторы объектов. Вы можете использовать их для работы с текстом (и даже для работы с графикой).

Рекуррентные нейронные сети (RNNs)

RNNs моделируют последовательности, применяя один и тот же набор весов рекурсивно к состоянию агрегатора в момент времени t и вход в момент времени t. Чистые RNN редко используются сейчас, но его аналоги, например, LSTM и GRU являются самыми современными в большинстве задач моделирования последовательности. LSTM, который используется вместо простого плотного слоя в чистой RNN.

Используйте RNN для любой задачи классификации текста, машинного перевода, моделирования языка.

Условные случайные поля (CRFs)

Они используются для моделирования последовательности, как RNN, и могут использоваться в сочетании с RNN. Они также могут быть использованы в других задачах структурированных прогнозирования, например, в сегментации изображения. CRF моделирует каждый элемент последовательности (допустим, предложение), таким образом, что соседи влияют на метку компонента в последовательности, а не на все метки, независимые друг от друга.

Используйте CRF для связки последовательностей (в тексте, изображении, временном ряду, ДНК и т. д.).

Деревья принятия решений и случайные леса

Один из самых распространённых алгоритмов машинного обучения. Используется в статистике и анализе данных для прогнозных моделей. Структура представляет собой “листья” и “ветки”. На “ветках” дерева решения записаны атрибуты, от которых зависит целевая функция, в “листьях” записаны значения целевой функции, а в остальных узлах – атрибуты, по которым различаются случаи.

Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной на основе нескольких входных переменных.

Источник

Алгоритмы машинного обучения: основные понятия

Машинное обучение использует широкий спектр алгоритмов для перевода наборов данных в прогнозные модели. Какой алгоритм сработает лучше, зависит от решаемой задачи.

Машинное обучение получило широкое распространение, но и еще более широкое непонимание. Коротко изложим основные понятия машинного обучения, обсудим некоторые из наиболее распространенных алгоритмов машинного обучения и объясним, как эти алгоритмы связаны с другими частями мозаики создания прогнозных моделей из исторических данных.

Что такое алгоритмы машинного обучения?

Машинное обучение – это класс методов автоматического создания прогнозных моделей на основе данных. Алгоритмы машинного обучения превращают набор данных в модель. Какой алгоритм работает лучше всего (контролируемый, неконтролируемый, классификация, регрессия и т. д.), зависит от типа решаемой задачи, доступных вычислительных ресурсов и характера данных.

Алгоритмы обычно напрямую говорят компьютеру, что делать. Например, алгоритмы сортировки преобразуют неупорядоченные данные в данные, упорядоченные по некоторым критериям, часто в числовом или алфавитном порядке одного или нескольких полей данных.

Алгоритмы линейной регрессии «подгоняют» прямую линию к числовым данным, как правило, выполняя инверсии матрицы, чтобы минимизировать значение квадрата погрешности между линией и данными. Квадрат погрешности используется в качестве метрики, поскольку не важно, находится ли линия регрессии выше или ниже точек данных — принципиально только расстояние между построенной линией и исходными точками.

Алгоритмы нелинейной регрессии, которые «подгоняют» кривые (например, многочлены или экспоненты) к данным, немного сложнее: в отличие от задач линейной регрессии для них не существует детерминистских подходов. Вместо этого алгоритмы нелинейной регрессии реализуют тот или иной итерационный процесс минимизации, часто — некоторую вариацию метода самого крутого спуска.

Самый крутой спуск в общем случае предполагает вычисление квадрата погрешности и ее градиента при текущих значениях параметров, выбор размера шага (он же — скорость обучения), следование направлению градиента «вниз по склону», а затем пересчет квадрата погрешности и ее градиента при новых значениях параметров. В конце концов, если повезет, все сойдется. Варьируя алгоритм самого крутого спуска пытаются улучшить его характеристики сходимости.

Алгоритмы машинного обучения еще сложнее, чем нелинейная регрессия, отчасти потому, что машинное обучение обходится без ограничения на «подгонку» к определенной математической функции. Есть две основные категории задач, которые часто решаются с помощью машинного обучения: регрессия и классификация. Регрессия – для числовых данных (например, каков вероятный доход для человека с данным адресом и профессией). Классификация – для нечисловых данных (например, сможет ли заемщик выплатить кредит).

Задачи прогнозирования (например, какова будет цена открытия акций «Яндекса» завтра) являются подмножеством регрессионных задач для данных временных рядов. Задачи классификации иногда подразделяют на бинарные (да или нет) и мультикатегории (животные, фрукты или предметы мебели).

Контролируемое обучение против неконтролируемого

Независимо от этих типов существуют еще два вида алгоритмов машинного обучения: контролируемые (supervised) и неконтролируемые (unsupervised). В контролируемом обучении формируется обучающий набор данных с ответами, скажем, набор изображений животных вместе с именами животных. Целью обучения будет модель, которая сможет правильно распознавать изображения (то есть узнавать животных, включенных в набор обучения), которые она ранее не видела.

При неконтролируемом обучении алгоритм сам просматривает данные и пытается получить значимые результаты. Результатом может быть, например, набор групп значений, которые могут быть связаны внутри каждой группы. Алгоритм работает надежнее, когда такие группы не пересекаются.

Обучение превращает контролируемые алгоритмы в модели, оптимизируя их параметры, чтобы найти набор значений, который наилучшим образом соответствует данным. Алгоритмы часто основываются на вариантах самого крутого спуска, оптимизированных для конкретного случая; пример — стохастический градиентный спуск (SGD), который является по существу самым крутым спуском, выполненным многократно от случайных начальных точек. Учет факторов, которые корректируют направление градиента на основе импульса или регулируют скорость обучения в зависимости на основе прогресса от одного прогона данных (его называют эпохой) к следующему, позволяют подобрать оптимальные настройки SGD.

Очистка данных для машинного обучения

Такой вещи, как чистые данные, не существует. Чтобы быть полезными для машинного обучения, данные должны быть сильно отфильтрованы. Например, можно:

Можно сделать еще много чего, но это будет зависеть от собранных данных. Это может быть утомительно, но, если шаг очистки данных в конвейере машинного обучения предусмотрен, в дальнейшем по желанию его можно будет изменить или повторить.

Кодирование и нормализация данных для машинного обучения

Чтобы использовать категориальные данные для машинной классификации, необходимо преобразовать текстовые метки в другую форму. Существует два типа кодировок.

Первая – нумерация меток, каждое значение текстовой метки заменяется числом. Вторая – «единая горячая» (one-hot) кодировка, каждое значение текстовой метки превращается в столбец с двоичным значением (1 или 0). Большинство платформ машинного обучения имеют функции, которые выполняют кодировку самостоятельно. Как правило, предпочтительной является единая горячая кодировка, поскольку нумерация меток иногда может запутать алгоритм машинного обучения, заставляя думать, что коды упорядочены.

Чтобы использовать числовые данные для машинной регрессии, данные обычно требуется нормализовать. В противном случае при вычислении евклидовых расстояний наборы чисел с большими диапазонами могут начать неоправданно «доминировать», а оптимизация самого крутого спуска может не сходиться. Существует несколько способов нормализации данных для машинного обучения, включая минимаксную нормализацию, центрирование, стандартизацию и масштабирование до единичной длины. Этот процесс также часто называют масштабированием.

Что такое признаки в машинном обучении?

Признак – это индивидуальное измеримое свойство или характеристика наблюдаемого явления. Понятие «признак» связано с понятием независимой переменной, которая используется в статистических методах, таких как линейная регрессия. Векторы признаков объединяют все признаки одной строки в числовой вектор.

Часть искусства выбора функций состоит в том, чтобы выбрать минимальный набор независимых переменных, которые объясняют задачу. Если две переменные сильно коррелированы, их необходимо объединить в одну или удалить. Иногда люди анализируют главные компоненты, чтобы преобразовать коррелированные переменные в набор линейно некоррелированных переменных.

Некоторые преобразования, используемые для построения новых признаков или уменьшения размерности их векторов, просты. Например, вычтя год рождения из года смерти, получают возраст смерти, который является главной независимой переменной для анализа смертности и продолжительности жизни. В других случаях построение признаков может быть не столь очевидным.

Общие алгоритмы машинного обучения

Существуют десятки алгоритмов машинного обучения, варьирующихся по сложности от линейной регрессии и логистической регрессии до глубоких нейронных сетей и ансамблей (так называют комбинации других моделей).

Вот некоторые из наиболее распространенных алгоритмов:

А где нейронные сети и глубокие нейронные сети, о которых так много говорят? Они, как правило, требуют больших вычислительных затрат, поэтому их следует использовать только для специализированных задач, таких как классификация изображений и распознавание речи, для которых не подходят более простые алгоритмы. («Глубокая» означает, что в нейронной сети много слоев.)

Гиперпараметры для алгоритмов машинного обучения

Алгоритмы машинного обучения обучаются на данных, чтобы найти лучший набор весов для каждой независимой переменной, которая влияет на прогнозируемое значение или класс. Сами алгоритмы имеют переменные, называемые гиперпараметрами. Они называются гиперпараметрами, потому что, в отличие от параметров, управляют работой алгоритма, а не определяемыми весами.

Наиболее важным гиперпараметром часто является скорость обучения, которая определяет размер шага, используемый при поиске следующего набора весов для оптимизации. Если скорость обучения слишком высока, крутейший спуск может быстро сойтись на плато или к неоптимальной точке. Если скорость обучения слишком низкая, спуск может остановиться и никогда полностью не сойтись.

Многие другие распространенные гиперпараметры зависят от используемых алгоритмов. Большинство алгоритмов имеют параметры остановки, такие как максимальное число эпох, максимальное время выполнения или минимальное улучшение от эпохи к эпохе. Определенные алгоритмы имеют гиперпараметры, которые управляют формой их поиска. Например, классификатор случайного леса имеет гиперпараметры для минимальных выборок на лист, максимальной глубины, минимальных выборок при расщеплении, минимальной массовой доли для листа и проч.

Некоторые платформы машинного обучения предусматривают автоматическую настройку гиперпараметров. По сути, системе следует сообщить, какие гиперпараметры надо изменить, и, возможно, какую метрику требуется оптимизировать, и система просматривает эти гиперпараметры столько запусков, сколько ей будет позволено. (Например, Google Cloud hyperparameter tuning извлекает соответствующую метрику из модели TensorFlow, поэтому вам не нужно ее указывать.)

Есть три подхода в оптимизации гиперпараметров: Байесовская оптимизация, поиск по решетке и случайный поиск. Как правило, самым эффективным подходом оказывается Байесовская оптимизация.

Можно предположить, что настройка как можно большего количества гиперпараметров даст лучший ответ. Однако, это может быть очень дорого. С опытом приходит понимание, какие гиперпараметры имеют наибольшее значение для исследуемых в каждом конкретном случае данных и выбранных алгоритмов.

Автоматизированное машинное обучение

Есть только один способ узнать, какой алгоритм или ансамбль алгоритмов даст лучшую модель в каждом случае, – попробовать все. Если также попробуете все возможные нормализации и варианты функций, неминуем с комбинаторным взрывом.

Пытаться все сделать вручную нецелесообразно, поэтому поставщики инструментов машинного обучения приложили много усилий для выпуска систем класса AutoML (так называемое автоматизированное машинное обучение). Лучшие из них сочетают в себе настройку параметров, подбор алгоритмов и нормализацию данных. Гиперпараметрическую настройку лучшей модели (или моделей) часто оставляют на потом.

Таким образом, алгоритмы машинного обучения – всего лишь часть мозаики машинного обучения. В дополнение к выбору алгоритма (вручную или автоматически) нужно будет иметь дело с оптимизаторами, очисткой данных, выбором функций, нормализацией и (необязательно) настройкой гиперпараметров.

Когда вы обработаете все это и построите модель, которая будет работать с вашими данными, придет время использовать модель, а затем обновлять ее по мере изменения условий. Однако управление моделями машинного обучения – уже совсем другая история.

Поделитесь материалом с коллегами и друзьями

Источник