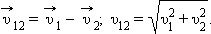Автомобиль движется по прямому шоссе вдоль которого направлена координатная ось х
Движение по окружности.



Теория: Будем рассматривать движение по окружности с постоянной по модулю скоростью.Скорость векторная величина, поэтому помимо численного значения она имеет направление. При движении по окружности, меняется направление скорости, т.е. меняется скорость следовательно, существует ускорение (центростремительное ускорение)
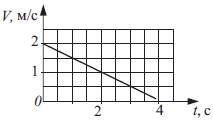
1.Скорость тела меняется с течением времени по закону, показанному на рис. Какой из участков графика соответствует равнозамедленному движению тела? Напишите начало этого участка (в секундах) и конец этого участка (в секундах) без пробела
4.Зависимость координаты материальной точки от времени задаётся уравнением x = 5 + 4t + 3t 2 (м). Какова начальная скорость точки? Ответ в м/с.
6.На рисунке приведена зависимость координаты материальной точки от времени. Какой путь прошла точка за 2 с? Ответ в м.
7.Для прямолинейного движения график зависимости модуля перемещения от времени имеет вид. Какой из графиков верно описывает зависимость пути от времени?
8.Во сколько раз нужно увеличить начальную скорость брошенного вверх тела, чтобы максимальная высота подъёма увеличилась в 4 раза?
9.На рисунке приведён график зависимости пути от времени для некоторого тела. Какова скорость тела в промежутке времени от 5 до 7 с? Ответ в м/с.
11. На рисунке приведён график зависимости проекции скорости от времени для некоторого тела. Какова средняя путевая скорость тела за 6 с? Ответ в м/с.
12. Автомобиль движется по прямой улице. На графике на рисунке представлена зависимость его скорости от времени. Найдите, какое расстояние проехал автомобиль на участке движения с постоянной скоростью. Ответ в км.
13. Тело бросили с поверхности Земли вертикально вверх. Сопротивления воздуха нет. Какой из графиков верно описывает зависимость проекции скорости тела на ось y от времени, направленную от поверхности Земли вертикально вверх?
14.На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке x = 0, а пункт Б — в точке x = 45 км. Чему равна максимальная скорость автобуса на всём пути следования туда и обратно? Ответ в км/ч.
15. Для прямолинейного движения график модуля вектора перемещения от времени имеет вид, изображенный на графике. Какой из графиков верно описывает зависимость проекции скорости от времени?




16. На графике представлена зависимость скорости тела, двигающегося по прямой вдоль оси Ox, от времени. Найдите на какое расстояние переместилось тело за первые 6 с движения. Ответ в м.
18. Тело движется вдоль оси Ox. На рис. приведён график зависимости проекции скорости тела νx от времени t. Какой путь прошло тело в интервале времени от 0 с до 6 с? Ответ в м.
20. На рисунке приведены графики зависимости пути от времени для тел А и В. Какова скорость тела В относительно тела А? Ответ в км/ч.
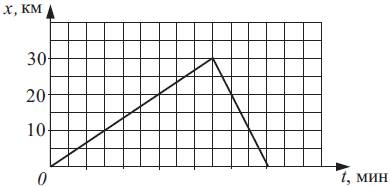
21.На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке x = 0, а пункт Б — в точке x = 30 км. Найдите сколько времени занял весь путь, если известно, что скорость автобуса на пути из пункта А в пункт Б была равна 60 км/ч. Ответ в мин.
22. С помощью графика определить путь, пройденный телом за 2 с. Ответ в метрах
23. Тело движется вдоль оси Ox. На рис. приведён график зависимости проекции скорости тела vx от времени t. Какой путь прошло тело в интервале времени от 3 с до 9 с? Ответ в м.
24. Автомобиль движется по прямому шоссе вдоль которого направлена координатная ось Ox. Начальная координата автомобиля равна 20 км. На рисунке представлен график зависимости проекции скорости автомобиля от времени..Определите конечную координату автомобиля. Ответ выразите в км и округлите до десятых. Ответ в км.
Тест №1 ЕГЭ по физике
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость автомобиля относительно земли ( v 1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v 2). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
Алгоритм решения
Решение
Записываем данные относительно Земли:
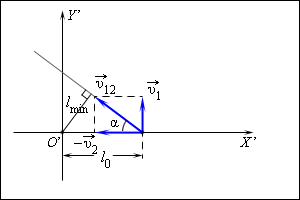
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость второго автомобиля относительно оси ОХ ( v 2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v 1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид :
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
Алгоритм решения
Решение
Весь график можно поделить на 3 участка:
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
Алгоритм решения
Решение
Запишем исходные данные:
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Алгоритм решения
Решение
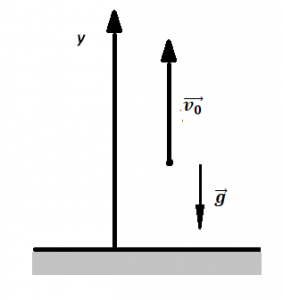
Записываем исходные данные:
Записываем формулу для определения скорости тела в векторном виде:
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
Подставим известные данные и вычислим скорость:
Алгоритм решения
Решение
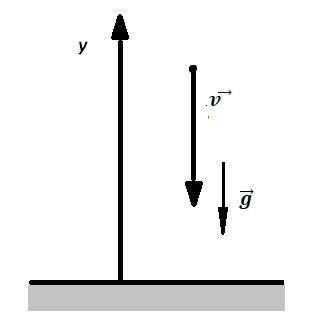
Записываем исходные данные:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Алгоритм решения
Решение
Записываем исходные данные:
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
 Задачи с решениями
Задачи с решениями 

Решение
Первый способ.
Положение каждого из автомобилей в любой момент времени можно задать двумя координатами. Выберем Землю в качестве тела отсчета. Направим координаты оси и вдоль дорог в направлении движения автомобилей (рис. 1.2.1). За начало координат выберем перекресток, за начало отсчета времени – момент пересечения перекрестка первым автомобилем. Уравнения движения автомобилей записываются в виде:
Расстояние между автомобилями в любой момент времени равно
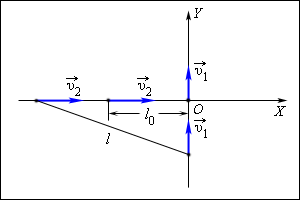 | ||
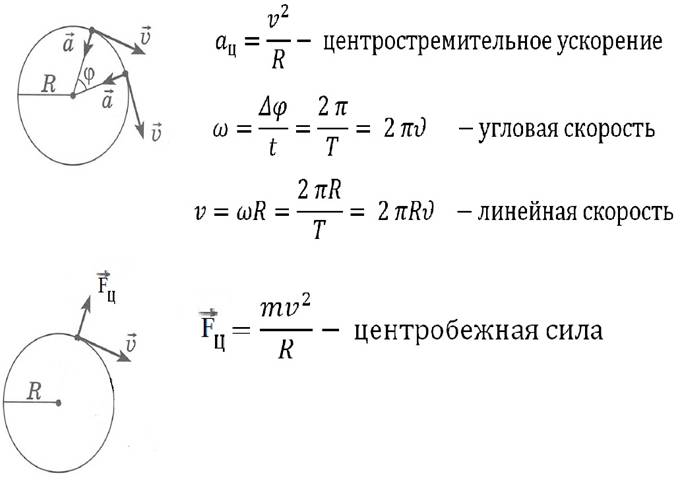
| Рисунок 1.2.1. В качестве тела отсчета выберем второй автомобиль; направление координатных осей и и начало отсчета времени примем такими же, как и в первом способе решения задачи. В системе отсчета, связанной со вторым автомобилем, первый автомобиль движется со скоростью Эта скорость направлена под некоторым углом к прямой, соединяющей автомобили в начальный момент времени (рис. 1.2.2).
|




































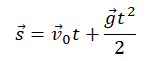
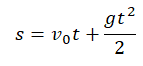
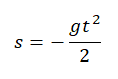
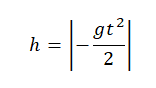
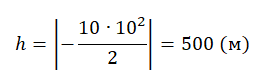



 Задачи с решениями
Задачи с решениями 

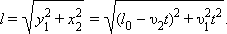
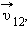 равной:
равной: