Автомобиль совершил разворот на 180 за 5 с каковы при этом

§ 7. Скорость (окончание)

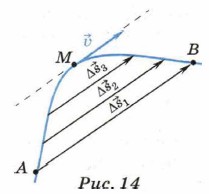
Убедимся в том, что мгновенная скорость в каждой точке траектории направлена по касательной к ней. Для этого выберем произвольную точку М траектории, а также точки А и B, лежащие на траектории на малых расстояниях по обе стороны от точки М (рис. 14).

Как следует из определения мгновенной скорости, её направление совпадает с направлением малого перемещения Δ. Последовательно сближая точки А и Б, будем получать всё меньшие векторы Δ₁, Δ₂, Δ₃ и т.д., параллельные друг другу. Чем ближе точки А и B, тем точнее отношение будет соответствовать вектору мгновенной скорости. Таким образом, вектор мгновенной скорости в точке М направлен по касательной к траектории.

Наиболее просто можно вычислить мгновенную скорость в случае равноускоренного движения.

Вопросы для самопроверки

1. Как вычисляется скорость равномерного прямолинейного движения?

2. Что называют средней скоростью; средней путевой скоростью?

3. Что называют мгновенной скоростью? Как она направлена в произвольной точке траектории?

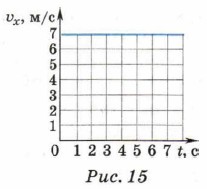
1. По графику зависимости υ_x = υ_x(t) (рис. 15) вычислите проекцию перемещения тела за 5 с.

2. Сравните понятия «средняя скорость» и «средняя путевая скорость».

3. Автомобиль совершил разворот на 180° за 5 с. Каковы при этом его средняя путевая скорость и модуль средней скорости, если радиус разворота 5 м?

4. Следуя по междугороднему маршруту, автобус до первой остановки проехал 50 км за час, затем остановился на полчаса, а после этого следовал без остановок 2,5 ч, проехав при этом 150 км. С какой средней скоростью двигался автобус?

5. Антилопа гну может двигаться со скоростью 80 км/ч, а акула — примерно 10 м/с. Кто из них перемещается быстрее и примерно во сколько раз?

Источник

§ 7. Скорость (окончание)

Убедимся в том, что мгновенная скорость в каждой точке траектории направлена по касательной к ней. Для этого выберем произвольную точку М траектории, а также точки А и B, лежащие на траектории на малых расстояниях по обе стороны от точки М (рис. 14).

Как следует из определения мгновенной скорости, её направление совпадает с направлением малого перемещения Δ. Последовательно сближая точки А и Б, будем получать всё меньшие векторы Δ₁, Δ₂, Δ₃ и т.д., параллельные друг другу. Чем ближе точки А и B, тем точнее отношение будет соответствовать вектору мгновенной скорости. Таким образом, вектор мгновенной скорости в точке М направлен по касательной к траектории.

Наиболее просто можно вычислить мгновенную скорость в случае равноускоренного движения.

Вопросы для самопроверки

1. Как вычисляется скорость равномерного прямолинейного движения?

2. Что называют средней скоростью; средней путевой скоростью?

3. Что называют мгновенной скоростью? Как она направлена в произвольной точке траектории?

1. По графику зависимости υ_x = υ_x(t) (рис. 15) вычислите проекцию перемещения тела за 5 с.

2. Сравните понятия «средняя скорость» и «средняя путевая скорость».

3. Автомобиль совершил разворот на 180° за 5 с. Каковы при этом его средняя путевая скорость и модуль средней скорости, если радиус разворота 5 м?

4. Следуя по междугороднему маршруту, автобус до первой остановки проехал 50 км за час, затем остановился на полчаса, а после этого следовал без остановок 2,5 ч, проехав при этом 150 км. С какой средней скоростью двигался автобус?

5. Антилопа гну может двигаться со скоростью 80 км/ч, а акула — примерно 10 м/с. Кто из них перемещается быстрее и примерно во сколько раз?

Источник