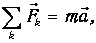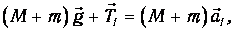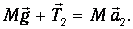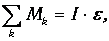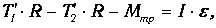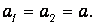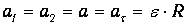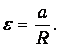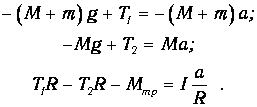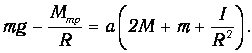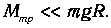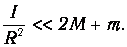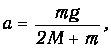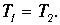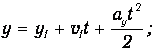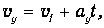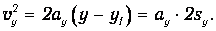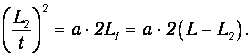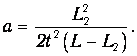Чем определяется ускорение грузов в машине атвуда

Изучение законов поступательного движения на машине Атвуда: формулы и пояснения

Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.

Что такое машина Атвуда?

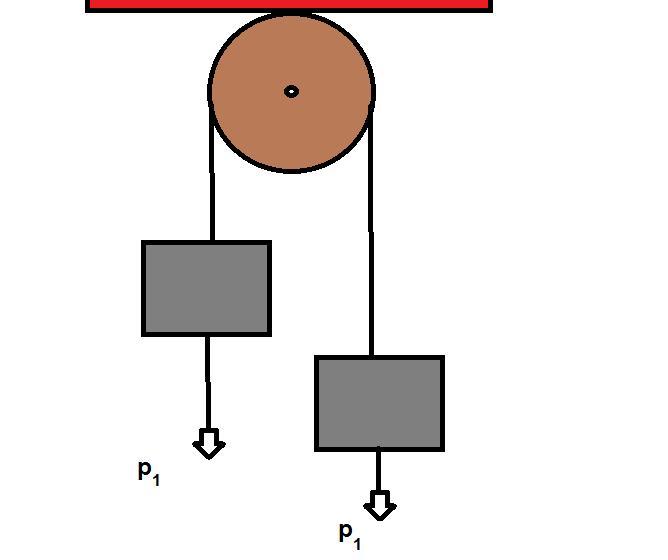
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Вам будет интересно: Пространственная экономика: описание специальностей и структура

Вам будет интересно: Что такое подполье? Подпольная организация «Молодая гвардия». Антифашистское движение

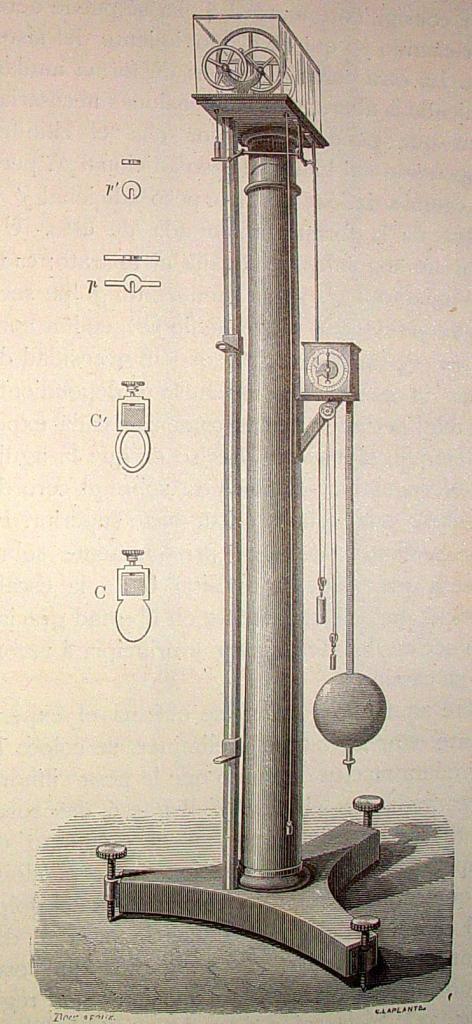
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.

Уравнения динамики

Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:

Где m – инерционная масса тела, a – ускорение.

Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.

Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:

Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:

Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.

Расчет уравнений динамики для равноускоренного движения

Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.

Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:

Чтобы выразить значение ускорения a, сложим оба равенства, получаем:

Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:

Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:

Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.

Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:

Откуда ускорение определяется однозначно:

Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:

Где m – количество измерений.

Приравнивая это равенство и полученное ранее, приходим к следующему выражению:

Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.

Расчет силы тяжести

Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:

Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:

Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:

Определение силы натяжения нити

Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:

Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:

T = (m2*F1 + m1*F2)/(m1 + m2).

Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:

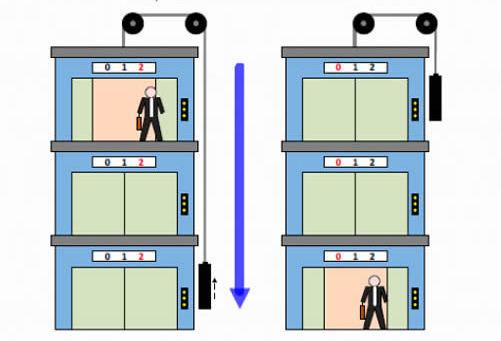
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.

Источник

Методические указания к лабораторной работе «Машина Атвуда»

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Экспериментальная проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение ускорения свободного падения лабораторной установке – машине Атвуда.

Время движения грузов измеряется с помощью ручного или стационарного секундомера.

Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити.

Второй закон Ньютона в проекциях на вертикальную ось для каждого из тел системы (рис.2) в предположении невесомости блока, отсутствия силы трения и нерастяжимости нити дает:

(1)

(2)

Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то

(3)

Третье соотношение часто называют законом перемещений: «Перемещение при равноускоренном движении прямо пропорционально квадрату времени движения».

Соотношение (3) может быть проверено экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение, с которым движется тело, прямо пропорционально равнодействующей действующих на него сил и обратно пропорционально массе этого тела».

Подставляя a _i в (2) получаем следующую формулу:

(4)

(5)

— сумма проекций на ось Z всех сил, действующих на вращающиеся тело; α- угловое ускорение блока; J – его момент инерции

(6)

Выразим из уравнения (1) разность сил натяжения ( T ₁ – T ₂ ) и подставив ее в уравнение (6) получим:

(7)

Выразим ускорение грузов a :

(8)

Учитывая, что значение момента инерции блока

(9),

k- коэффициент распределения массы блока относительно оси вращения (k

11)

Задание 1. Проверка второго закона Ньютона.

Поскольку ускорение движения является функцией двух переменных – силы и массы, то изучение второго закона Ньютона выполняется путем раздельного исследования двух зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе системы и 2) зависимости ускорения от массы системы при постоянной действующей силе.

Исследование зависимости ускорения от силы при постоянной массе

Измерения и обработка результатов

3. Измеряют время равноускоренного движения системы на пути, например, 1 метр. Все данные заносят в таблицу 1.3 отчета.

4. Пользуясь законом путей (1.6), вычисляют ускорение а.

5. Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.

6. Строят график зависимости ускорения движения от действующей силы. Точку ( F =0, a =0) на графике не откладывают. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о том, что ускорение действительно прямо пропорционально силе.

7. По угловому коэффициенту полученной прямой определяют массу системы и сравнивают ее реальной массой.

Исследование зависимости ускорения от массы при постоянной силе

Измерения и обработка результатов

1. Все опыты проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе. Ускорение системы измеряется также как и в предыдущем задании.

2. Для изменения массы системы одновременно на правый и левый груз кладут дополнительные одинаковые грузы. Все данные записывают в таблицу отчета.

3. График обратно пропорциональной зависимости ускорения от массы представляет собой гиперболу, которую невозможно идентифицировать. Для проверки предположения об обратно пропорциональной зависимости между ускорением и массой необходимо построить график зависимости ускорения от обратного значения массы системы: a = f (М -1 ). Подтверждением предположения является прямолинейность этого графика.

4. По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе

Задание 2. Определение ускорения движения грузов

В полученном уравнении прямой коэффициент k равен половине ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов ( a =2 k ) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.

Задание 3. Определение ускорения свободного падения

(Выполняется по результатам измерений и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и перегрузка, а также ускорение движения системы, из формулы (3) найдите ускорение свободного падения. Результаты занесите в отчет. В выводе сравните полученный результат с табличной величиной.

Для нахождения погрешности измерения величины ускорения свободного падения Δ g используем формулу:

12)

где ; ; ; ;

– частные производные функции

Проанализируйте результаты своих наблюдений и сформулируйте вывод.

Контрольные вопросы

Какое движение называется поступательным?

Дайте определение инерциальной системы отсчета. Приведите примеры ИСО.

Сформулируйте первый закон Ньютона. Приведите примеры его проявления.

Дайте определение инертной массы тела. Гравитационной? От чего и как зависит масса тела?

Сформулируйте второй закон Ньютона. Приведите варианты его математической формы.

Покажите все силы, действующие на один из грузов в машине Атвуда, и составьте для него уравнение динамики.

Запишите систему уравнений динамики для машины Атвуда с учетом момента инерции блока. Силы трения в блоке?

Источник

Описание лабораторной работы

Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

называют основным уравнением динамики.

Эскиз машины Атвуда показан на рис. 1.

Рис. 1. Эскиз машины Атвуда

Основное уравнение динамики для груза с перегрузком имеет вид:

а для другого груза (без перегрузка):

Основное уравнение динамики вращательного движения неподвижного блока имеет вид:

Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим

Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:

Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:

Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:

В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство

Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:

Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m :

а модули сил натяжения нити Т₁ и Т₂ по обе стороны блока равны:

Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).

Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:

Система грузов перемещается на величину s_y=L₁ , двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).

С помощью формулы (15) найдём расчётную формулу для величины ускорения а грузов с перегрузком:

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Рис. 2. Схема экспериментальной установки

Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.

6. Нажмите кнопку «СБРОС».

8. Вычислите среднее значение времени t >. Результат занесите в таблицу расчетов 2.

Источник

Изучение динамики поступательного движения тела и определение ускорения свободного падения с помощью машины атвуда

Цель работы: изучение динамики поступательного движения тела в поле сил земного тяготения, определение ускорения свободного падения.

Приборы и принадлежности: машина Атвуда со встроенным милли-секундомером, набор грузов и разновесов.

Общие теоретические сведения

Простейшей и в то же время наиболее часто встречающейся и привычной нам формой движения в природе является Механическое движение, состоящее в изменении взаимного расположения тел или их частей.

Раздел физики, занимающийся изучением закономерностей механического движения и взаимодействия тел, называется Механикой. При этом под Механическим действием на тело понимают такое воздействие со стороны других тел, которое приводит к изменению состояния механического движения рассматриваемого тела или к его Деформации, то есть к изменению взаимного расположения его частей.

Механику тел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме м/с), называют Классической механикой в отличие от Релятивистской механики быстро движущихся тел. Основы классической механики были разработаны И. Ньютоном.

Основным разделом механики является Динамика, занимающаяся исследованием влияния взаимодействия тел на их механическое движение.

Материальной точкой называется тело, форма и размеры которого несущественны в данной задаче. Любое протяжённое тело или систему тел, образующих исследуемую механическую систему, можно рассматривать, как Систему материальных точек.

Абсолютно твёрдым телом называется тело, расстояние между любыми двумя точками которого всегда остаётся неизменным. Эта модель пригодна в тех случаях, когда в рассматриваемой задаче деформации тела при его взаимодействии с другими телами пренебрежимо малы.

Для однозначного определения положения исследуемого тела в произвольный момент времени необходимо выбрать систему отсчёта. Системой отсчёта называется система координат, снабжённая часами и жёстко связанная с абсолютно твёрдым телом, по отношению к которому определяется положение других тел в различные моменты времени. При этом под часами подразумевается любое устройство, используемое для измерения времени или, точнее, промежутков времени между событиями, так как в силу однородности времени начало его отсчёта можно выбирать произвольно. В ньютоновской механике предполагается, что свойства пространства описываются геометрией Евклида, а ход времени одинаков во всех системах отсчёта.

В основе классической динамики лежат три закона Ньютона, сформулированные в его сочинении “Математические начала натуральной философии”, которое было впервые опубликовано в 1687 г. Эти законы явились результатом гениального обобщения тех частных опытных и теоретических закономерностей в области механики, которые были установлены Ньютоном и такими выдающимися его предшественниками и современниками, как И. Кеплер, Г. Галилей, Х. Гюйгенс, Р. Гук и др.

В качестве первого закона динамики Ньютон принял закон, установленный ещё Галилеем. Первый закон Ньютона гласит: Всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит его (её) изменить это состояние.

Первый закон Ньютона утверждает, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания каких-либо внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое Инертностью. Соответственно первый закон Ньютона называют также Законом инерции, а движение тела, свободного от внешних воздействий, — Движением по инерции.

Системы отсчёта, по отношению к которым выполняется закон инерции, называются Инерциальными системами отсчёта. Опыты показали, что с очень большой степенью точности можно считать инерциальной Гелиоцентрическую систему отсчёта.

В качестве меры механического действия одного тела на другое в механике вводится векторная величина, называемая Силой. Сила полностью задана, если указаны её модуль , направление в пространстве и точка приложения. Прямая, вдоль которой направлена сила, называется Линией действия силы.

Опыты показали, что под действием силы свободное твёрдое тело изменяет свою скорость , приобретая ускорение . Это ускорение пропорционально силе и совпадает с ней по направлению:

, (1)

Где — положительная скалярная величина, называемая массой тела. Чем больше инертность тела, а следовательно, и его масса , тем меньшее ускорение оно должно приобретать под действием одной и той же силы .

В ньютоновской механике масса материальной точки не зависит от времени , а ускорение , где — скорость точки. Поэтому уравнение (1) можно переписать в форме

. (2)

Вектор , равный произведению массы материальной точки на её скорость, называется Импульсом материальной точки.

Основной закон динамики материальной точки или второй закон Ньютона, записанный в форме (2), утверждает, что Скорость изменения импульса материальной точки равна действующей на неё силе.

Основной закон динамики материальной точки выражает Принцип причинности в классической механике, так как устанавливает однозначную связь между изменением с течением времени состояния движения и положения в пространстве материальной точки и действующей на неё силой.

Наблюдения и опыты свидетельствуют о том, что механическое действие двух тел друг на друга всегда является их взаимодействием. Если тело 2 действует на тело 1, то при этом обязательно тело 1, в свою очередь, действует на тело 2.

Количественное описание механического взаимодействия материальных точек было дано Ньютоном в третьем законе динамики: Две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны вдоль соединяющей эти точки прямой.

, (3)

Где — сила, действующая на второе тело со стороны первого, — на первое со стороны второго.

Описание лабораторной установки

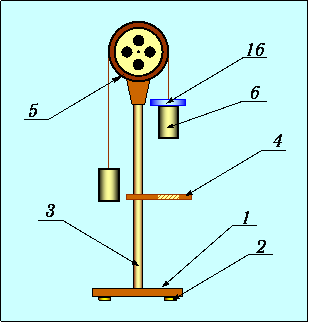
Машина Атвуда используется для изучения законов динамики движения тел в поле земного тяготения. Устройство машины Атвуда изображено на рисунке. Она представляет собой настольный прибор, состоящий из вертикальной стойки 1 и основания 2, на которых расположены три кронштейна (нижний 3, средний 4 и верхний 5) и электронный блок (миллисекундомер) 10. На верхнем кронштейне крепится малоинерционный шкив 11 с узлом подшипников качения, через который перекинута нить 7 с грузами А и Б, имеющими массы и соответственно.

На верхнем кронштейне также находится электромагнит 8, который при подаче на него напряжения с помощью фрикциона удерживает систему с грузами в неподвижном состоянии. На среднем кронштейне 4 крепится фотодатчик 9, который выдает электрический сигнал окончания счёта времени равноускоренного движения грузов А и Б (если масса груза Б больше массы груза А). Средний кронштейн имеет метку, положение которой совпадает с оптической осью фотодатчика (риска на корпусе).

Нижний кронштейн 3 представляет собой площадку, которая используется для гашения удара груза Б при падении. Средний и нижний кронштейны могут свободно перемещаться и фиксироваться на вертикальной стойке по всей её длине. На вертикальной стойке 1 нанесена миллиметровая линейка, по которой определяют начальное и конечное положения груза Б, а следовательно, и пройденный путь S. При этом начальное положение груза Б определяют с помощью визира 6 по нижнему срезу груза, а конечное положение — по соответствующей метке среднего кронштейна с фотодатчиком.

Ускорение свободного падения g можно найти с помощью очень простого опыта: бросить тело с высоты H И измерить время падения T. Тогда

.

В действительности дело обстоит не так просто, если величину G Требуется определить достаточно точно.

Время падения материальной точки с высоты М при равно

С.

При измерении такого промежутка времени с погрешностью ±0,01С относительная погрешность определения G, равная , будет более 4,5 % и абсолютная погрешность . Казалось бы, чтобы снизить погрешность определения , используя секундомер с той же погрешностью , надо увеличить измеряемый промежуток времени, увеличивая высоту падения. Так, при время падения около 1 С, а при — . Однако в этом случае возникают ошибки другого характера. Дело в том, что при больших скоростях заметную роль играет сопротивление воздуха, а формула равноускоренного движения этого фактора не учитывает. Таким образом, увеличивая высоту H, мы увеличиваем время падения и уменьшаем относительную погрешность его измерения, но при этом вносим другую ошибку: сама формула становится неточной. Например, если сбросить кирпич с высоты , то около он будет двигаться с ускорением, а затем сила сопротивления воздуха станет равной силе тяжести (это будет при скорости около ) и тело остальные будет двигаться с постоянной скоростью.

Приведенный простой пример наглядно демонстрирует общую черту любого физического эксперимента. В любом эксперименте точность определения какой-либо физической величины связана не только с точностью измерительных приборов, но и с тем, насколько точно принятая модель описывает данный опыт, иначе говоря, насколько модель адекватна экспериментальной ситуации.

Итак, сложности такого внешне простого опыта связаны с большим ускорением тела, за которым мы следим во время опыта. Так как ускорение большое, то тело быстро набирает скорость, а при этом или время движения мало и его трудно измерить, или сама формула равноускоренного движения неточна.

Уменьшить ускорение можно с помощью устройства, которое называется машиной Атвуда (см. рис.). Через блок перекинута нить, на которой укреплены грузы массами и . Если , то система начнет двигаться с ускорением , проходя расстояние . Для достижения цели — как можно более точного для наших условий определения ускорения свободного падения необходимо построить модель экспериментальной ситуации, которая реализуется в машине Атвуда. В рамках этой модели надо найти связь между , и и указать метод определения из такой зависимости интересующей нас величины .

Наиболее простая модель нашей экспериментальной установки такова: блок и нить невесомы, нить нерастяжима; трением в блоке и сопротивлением воздуха можно пренебречь.

Выберем неподвижную систему координат, центр которой совмещен с осью блока 11. Ось координат Ох направим вниз. В этом случае действующие в системе силы будут направлены вдоль этой оси и не потребуется векторной формы записи основных законов динамики. На груз Б действуют две силы: сила тяжести, равная , и сила натяжения нити, равная .

Согласно второму закону Ньютона

, (4)

Где — ускорение свободного падения, — ускорение груза Б.

На второй груз А также будут действовать две силы: и . В силу нерастяжимости нити ускорение груза А равно ускорению груза Б по абсолютной величине и направлено в противоположную сторону. Тогда из второго закона Ньютона следует, что

. (5)

Так как масса блока мала, то

. (6)

Вычитая из (4) (5) и учитывая (6), получаем

. (7)

Измеряя пройденный грузом Б путь S и время движения T, можно проверить равноускоренный характер движения груза Б:

. (8)

Определение ускорения свободного падения можно провести на основе формулы (7). Пусть – экспериментальное ускорение, вычисленное из (8). Подставляя в (7), получаем

. (9)

Учитывая выражение (8), ускорение свободного падения можно рассчитать следующим образом

. (10)

Из второго закона Ньютона вытекает следующее следствие. Если на тело постоянной массы действовать различными силами и , то согласно второму закону Ньютона, тело будет двигаться с разными ускорениями и , отношение которых равно отношению сил:

, при . (11)

Если же к телам с различными массами и приложить равные силы, то тела будут двигаться с разными ускорениями и , отношение которых обратно пропорционально отношению масс:

, . (12)

На машине Атвуда массы грузов А и Б одинаковы в исходном состоянии, то есть . Если масса правого груза Б будет больше массы левого груза А на , то система грузов А и Б будет двигаться равноускоренно с ускорением . Масса всей системы будет равна

.

Если к левому и правому грузам добавить перегрузки одинаковой массы , то сила, сообщающая системе ускорение, не изменится. Но система грузов будет двигаться с другим ускорением , так как изменилась движущая масса. Масса системы увеличилась на и стала равной

.

Отношение этих масс системы

. (13)

В обоих случаях система, двигаясь равноускоренно, проходит одно и то же расстояние , поэтому

. (14)

Из равенства (14) можно найти отношение ускорений

. (15)

Подготовка лабораторной установки к работе

1. Убедитесь, что система грузов А и Б с нитью, перекинутой через блок, находится в положении безразличного равновесия.

2. Если система не находится в положении безразличного равновесия, произведите регулировку положения основания с помощью регулировочных опор, используя для визуального наблюдения в качестве отвесов нить с грузами. При этом необходимо добиться вертикального положения стойки 1.

3. Установите кронштейн с фотодатчиком в нижней части шкалы миллиметровой линейки таким образом, чтобы правый груз при движении проходил посередине рабочего окна фотодатчика.

4. Включите в сеть шнур питания электронного блока.

Порядок выполнения работы

Задание 1. Проверка равноускоренного характера движения грузов машины Атвуда

1. Включить тумблер “сеть”, расположенный на задней стороне миллисекундомера.

2. С левого наборного груза А снять разновес массой 10 г. Тогда масса левого груза А будет равна 140 г, а правого груза Б — 150 г.

3. Отвести визир 6 от кронштейна с фотодатчиком 4 на расстояние (см. табл. 1).

4. Нажать кнопку “пуск” и, удерживая груз А, подвести нижнее основание наборного груза Б к верхнему краю визира. Затем нажать кнопки “стоп” и “сброс”. После срабатывания электромагнитного тормоза 8 отпустить груз А, при этом система грузов А и Б должна оставаться неподвижной.

5. Нажать кнопку “пуск” миллисекундомера и после пересечения грузом Б оптической оси фотодатчика и его остановки занести в табл. 1 показание таймера, то есть время движения грузов .

6. Повторить пп. 4-5 ещё два раза, записав показания прибора.

7. Повторить пп. 3-6 для ещё двух расстояний .

8. Для обеспечения разности масс грузов А и Б, равной 20 г, нужно с левого груза снять разновес массой 20 г. При этом десятиграммовый разновес, снятый во втором пункте, должен быть одет и находиться в составе наборного груза А. Тогда масса груза А будет равна 130 г, а масса груза Б останется равной 150 гр.

10. Для увеличения разности масс грузов А и Б до 30 г дополнительно снять с левого груза разновес массой 10 г. Тогда масса груза А станет равной 120 г.

11. Повторить пп. 3-7.

12. Рассчитать и для каждого значения и расстояния , которое проходят грузы А и Б. Оценить систематическую и случайную Составляющие, а также полную погрешность определения времени движения грузов по формулам

, , ,

Где — цена деления или точность миллисекундомера, — коэффициент Стьюдента ( при ).

Точность определения времени по миллисекундомеру составляет .

13. Для проверки равноускоренного характера движения грузов А и Б изобразить графически полученные результаты в координатах и , соответствующие каждому значению . По тангенсам углов наклона полученных прямых рассчитать ускорения, с которыми движутся грузы

.

, г

, г

, см

, с

, с

, с

, с

, с2

, м/с2

, м/с2

, м/с2

Источник