Что идет после куба

Тессеракт и прочие гиперкубы.

Стукнула тут меня мысль нарисовать куб в десятом измерении. Ну точнее проекцию на двухмерный экран. Думал думал думал… Ну теперь когда придумал, все кажется таким простым, но тем не менее думал я напряжно. Да и тему сначала понять надо было.

В общем что такое куб в четвертом измерении.. Будем рассматривать через проекцию на третье.

Начнем с точки. Точка вытягивается в линию Это первое измерение. Линия расползается в квадрат, второе.

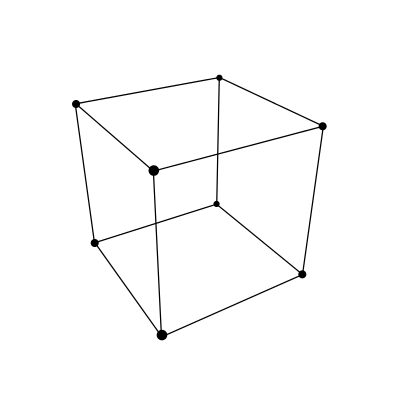
Квадрат раздваивается и расходится образуя куб.

А далее таким же методом вытягиваем куб из куба, и соединяем соответствующие точки.

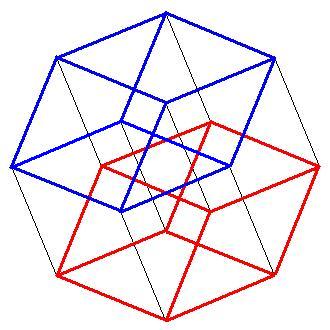
Вот пример каждая точка красного куба соединена с соответствующей точкой синего.

Тессеракт

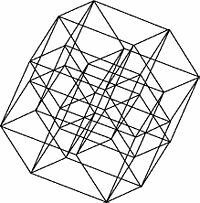
Далее идет пятое (тут я уже не стал возиться с обводкой)

Пентеракт

Хексеракт

Хептеракт

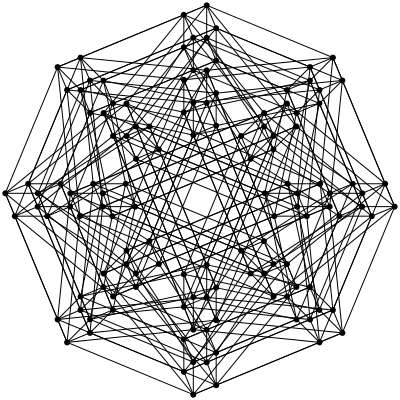
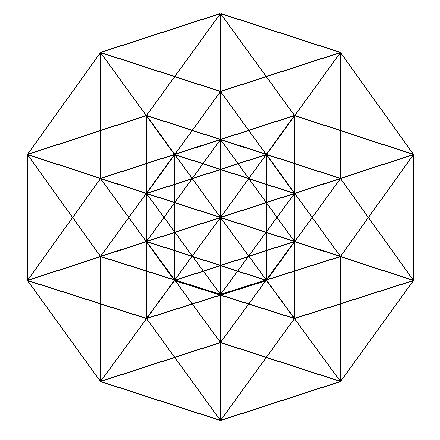
Октеракт

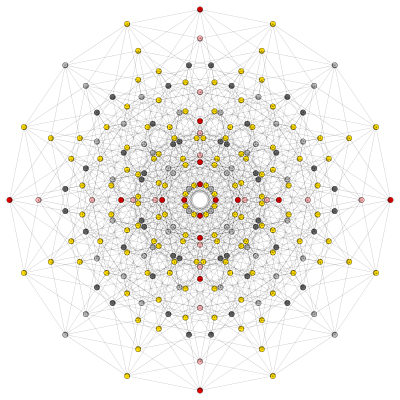
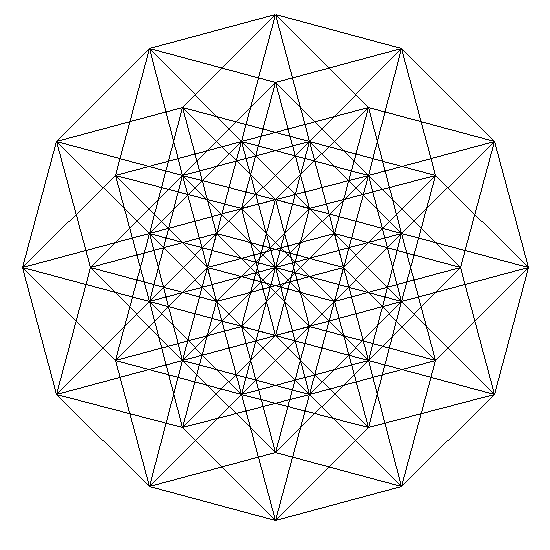
Энтенеракт

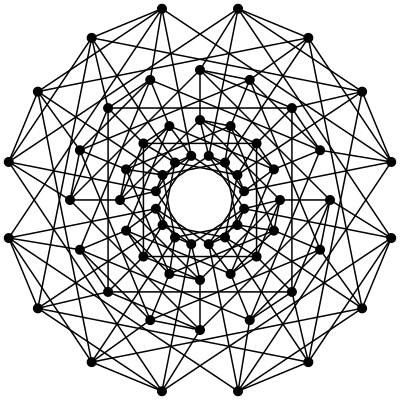
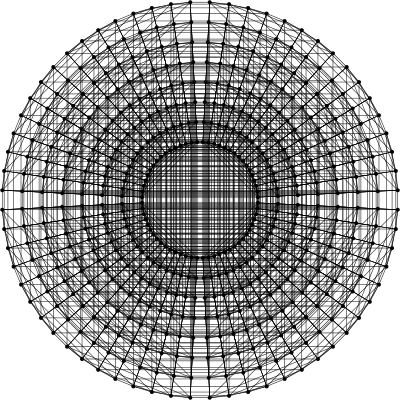
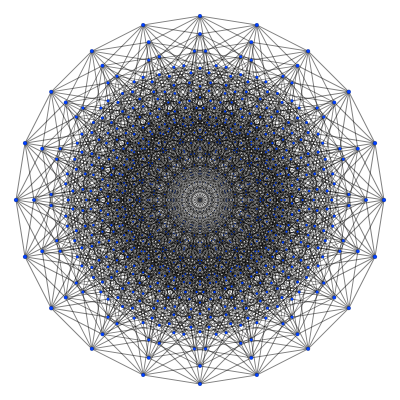
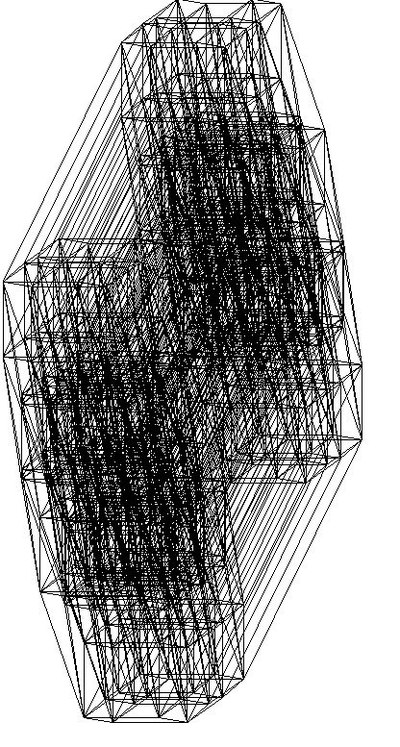
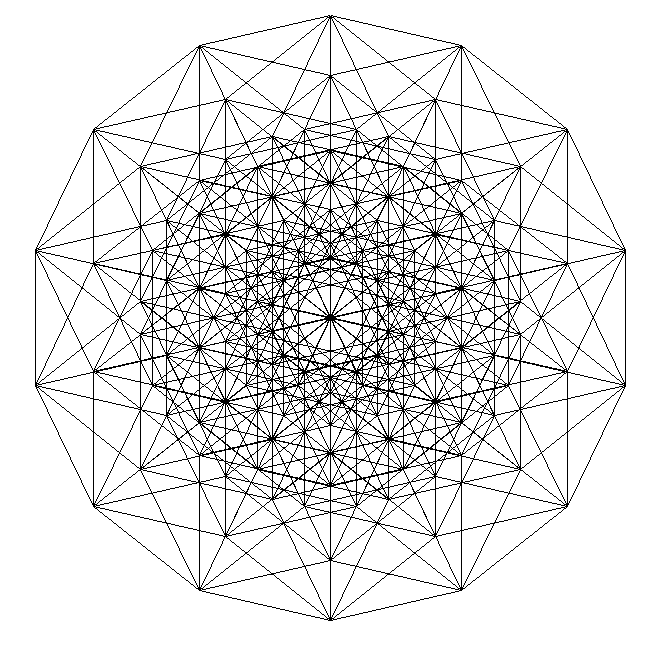
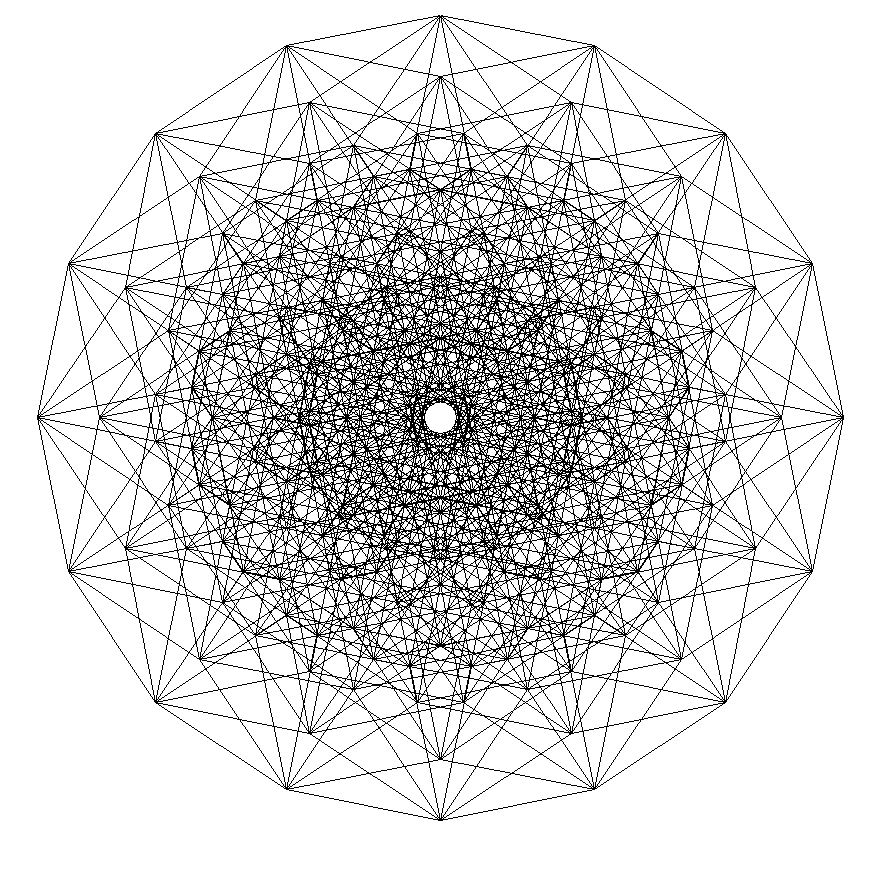
И десятимерный куб

Можно конечно и большие размерности и размеры (у меня тут файл 5000х5000 11мерный куб. вес правда всего 3 метра с небольшим) Но это уже если объявится желающий.

Да вот иногда я пишу подобную белеберду вместо кнопок бабло 🙂

54 thoughts on “ Тессеракт и прочие гиперкубы. ”

дружище ты бы к психологу сходил что ли 🙂
тесеракты какие то выдумываешь.

в пол седьмого утра точно бы не пошел, а вот попозжа может и прогулялся бы

Это ж надо было додуматься:) Хотя выглядит красиво, это да…

А на каком языке и с помощью каких библиотек реализовал это? Можно сделать скринсэйвер и выложить в паблик кстати.

На Делфи. рисовал стандартными процедурами на канве.

привет.
почты не нашел, а в аську по пустяку барабанить не хотеxtncz. Есть пару вопросов ричклику — судя по постам, ты с ними работаешь. Как у них с выплатами, задерживают как и сам бегун, или платят исправно как Зорька? Что нужно для аппрува, тупо дор какой-то общетематический в индексе показать, или что?
Заранее благодарен, пост можешь тереть, а ответить на почту, если не тяжело, ибо у тебя нет подписки)

Платят нормально.
Даты последних 8 платежей
20.10.2009
05.10.2009
17.09.2009
04.09.2009
19.08.2009
20.07.2009
25.06.2009
05.06.2009

Для апрува аккаунта надо показать свою вменяемость и адекватность.

Да, меня пример дора попросили показать. Спросили о трафике, о опыте, о том на каких форумах зареган и какова активность.
Уников на момент регистрации имел только 200 вместо 2к.

(Продублировал на почту)

Даже обычный гиперкуб 4-х мерный изобразить на плоскости невозможно, видел где-то в виде анимации, но все равно не то:) А то что вы изобразили это получается как бы тень от металлического каркаса таких фигур.

Я тоже видел анимацию.

Изобразить на плоскости объект большей мерности конечно невозможно. Не возможно изобразить даже обычный трехмерный куб. Поэтому изображение куба называется проекцией на плоскость.

о чем я и написал в посте словами «Ну точнее проекцию на двухмерный экран.»

Более того когда ты сказал «тень от металлического каркаса» ты сделал проекцию на трехмерность, то есть упростил гиперкуб в этот самый металлический каркас.

Так и я упростил всё до плоского изображения.

Хотя если совсем точно то тут изображенны проекции на плоскость трехмерных изображений, которые получены путем проекции гиперкубов в трехмерность.

Выложи программку что ли 🙂 с исходниками

Да какие исходники.. я программированию не обучен, поэтому думаю любого человека код введет в ступор.

На крайний случай я могу описать алгоритмы в отдельном посте. В конце концов именно в алгоритмах 90% сложности этой программы.

вот это офигеть. жги еще. на самом деле. вот у меня вопрос такой: ты можешь представить это все свое творчество в объеме? просто у меня например с этим всегда были траблы.. начиная с 4-го измерения, 3-х мерное пространство — 3 взаимно-перпендикулярных координатных оси, 4-х мерное пространство 4 оси. Куда ее пристроить-то? Ты я смотрю просто берешь и смещаешь трехмерный куб в разных направлениях, т.е каждая последующая мерность — реализуется виде некоторого движения. Это здорово, но все таки не то. В итоге получаешь просто траекторию движения точек куба, чем больше направлений смещения берешь,тем больше размерность. Однако, навряд ли это именно то, что происходит в действительности. Напиши, что думаешь по этому поводу.

Виноват. Вот перечитал пост свой. Все верно. Натупил слегка. Не о том подумал.

По факту это все проекции на третье измерение.

Думаю представить четвертое геометрическое пространство можно только абстрактно, но не визуально. Так как визуально все упирается в 2 и 3 мерность.

И даже если вспомнить разбитие на плоскости как это было в черчении, то трехмерный объект это просто три плоскости. А четырехмерный значит 4 объемности. (Смотря с каждой из четырех мерностей мы будем видеть трехмерный объект) формально четырехмерный объект будет описан, но чтобы представить его нужно иметь другой мозг.

И каждое новое смещение можно рассматривать как представление новой грани.. То есть мы копируем объект придавая ему еще одну глубину, будто бы мы посмотрели на объект с такого ракурса где видна новая ось. Но эти новые грани будут изначально трехмерными проекциями.
Если отойти от условностей и сделать многомерный куб в третьем измерении, то это будет тот же самые трехмерный куб, потому что для человеческого мозга не существует 4 геометрического измерения… Это как если бы человек из плоскости смотрел на куб, то он видел бы только квадрат.

Можно представить четвертое измерение как плоский срез пространства, имеющий глубину. Но это опять же проекция третьего измерения, где глубину третьего измерения подменяют глубиной четвертого.

Я вообще как то заморочился с перелинковкой сетки сателлитов в 400 штук такою штуку навоял парни долго потом всматривались в итоге сказали что надо лечиться,сейчас эта перелинковка цветет и процветает.
Извини за офтоп!!Но твои фигуры просто мне напомнили это!

Автор? ты что фентези перечитал? ил переиграл малость?

Отвечу на вопросы по очереди.
Автор
Перечитал
Переиграл
🙂

Мне думается что тесеракт- это просто невозможная фигура, как например треугольник из брусков у которого все углы по 90 градусов, просто интересная безделушка. А 4-ое измерение это из научной фантастики, одни лишь теории.

Да фигура невозможная, потому что человек не способен воспринимать 4 геометрическое измерение.

По повожу фантастики.
Когда программисты задают массив, они вполне могут сделать его четырех, пяти и более мерным.

Поэтому надо четко понимать о каком измерении идет речь. В широком смысле под четвертым измерением понимают время.
В узком геометрическом это просто дополнительная «глубина», которую человек не способен воспринять, и поэтому бОльшие мерности представляются проекциями на третье.
Поэтому, да. большие геометрические мерности существуют только теоретически.

«Это как если бы человек из плоскости смотрел на куб, то он видел бы только квадрат.»
А мне почему-то кажется, что если бы человек из плоскости смотрел на куб, то он видел бы его лишь как линию. Он мог бы понять, что это квадрат(не куб, заметьте, для двумерного человека понятие куб абстрактное, как для нас трёхмерных абстрактным является тессеракт) лишь в том случае, если бы ходил вокруг этого квадрата, изменение скорости удлиннения/укорачивания видимой линии служило бы показателем того, что там есть угол.

третье измерение глубина.
На плоскости мы будем видеть ширину и высоту, достаточно чтобы построить квадрат.

Если нарисовать на листе человечка и рядом квадрат, то конечно он его увидит как линию. Но как мы смотрим на плоскость (ведь изображение просто проецируется на сетчатке) и уже потом додумываем объем, так и он имея две оси вполне сможет понять, что перед ним квадрат.

И мне кажется обсуждение ушло куда то не туда.
Еще раз повторюсь это просто геометричекие проекции.

Я имею ввиду, что он живёт на плоскости, понятий «верх\низ» просто нет, как двумерный человек может посмотреть на плоскость сверху? Ведь «сверху» для него является третьим(гипотетическим) измерением. =))

если нет высоты то, тогда есть ширина и глубина. В любом случае есть два измерения а их достаточно для квадрата, на то она и плоскость.

Меня видимо поразило внезапное косноязычие, если я так долго не могу донести свою мысль… Представьте, что вы двумерный человек живущий на плоскости, посмотрите его глазами, как вы выберетесь в третье измерение(посмотрите сверху на плоскость, которая имеет длину и ширину)? Я прекрасно понимаю, что плоскости достаточно чтобы построить квадрат. А вот чтобы его увидеть нужно ещё одно измерение.
«…если бы человек из плоскости смотрел на куб, то он видел бы его лишь как линию. Он мог бы ПОНЯТЬ, что это квадрат», НО не смог бы увидеть.

Так же как и мы видим плоские объекты а не объемные. Но без всяких проблем рассуждаем о объеме.

И разве это
«Если нарисовать на листе человечка и рядом квадрат, то конечно он его увидит как линию. Но как мы смотрим на плоскость (ведь изображение просто проецируется на сетчатке) и уже потом додумываем объем, так и он имея две оси вполне сможет понять, что перед ним квадрат.» я не о том же самом говорил?

Поэтому я и говорил о высоте. он же своими глазами не только вперед-назад смотрит, но и вверх-вниз

тем не менее Penteract и Septeract существуют в виде матеиатических констант.

всё же, нарисовать 4х мерный объект в 3х мерном виде и поместить на 2х мерный экран, всё равно мы увидим не то, даже если предположить существование четвертого измрения

Вы всерьез думаете, что я не видел те картинки?
Мои картинки имеют равные грани, те — нет. Приглядитесь.

класс. молодец. а то народ совсем тупой

Уважаемый Elsper! (Извините, не знаю как правильно к Вам обратиться).
Я безмерно рада, увидев Ваши чертежи. Вы чертите ГОРИЗОНТАЛЬНЫЕ проекции трёхмерных проекций многомерных гиперкубов. И эти трёхмерные проекции многомерных гиперкубов (любых измерений!) можно чертить и во фронтальной, профильной проекциях, и в абсолютно в любых ракурсах. Более того, с помощью трубочек и лески я легко создала сами трёхмерные проекции четырёхмерного, пятимерного и шестимерного гиперкубов, на семимерный у меня не хватает трубочек.
Я написала работу «»Начала» геометрии многомерных измерений», в которой мною выявлен и подробно описан «Универсальный метод построения (черчения) трёхмерных проекций гиперкубов любых n-мерных измерений (3ПГК-n) в любых проекциях и ракурсах». Моя работа — это рукопись, правда, отсканированная, — потому что во время написания моих работ у меня не было компьютера, более того, я и сейчас, имея компьютер, не могу толком научиться чертить чертежи на компьютере — старая я, мне 64 года.
Уважаемый Elsper! Если Вам интересно прочитать или хотя бы просмотреть мою работу (где, кстати, я начертила горизонтальную проекцию трёхмерной проекции ДВЕНАДЦАТИМЕРНОГО гиперкуба), пожалуйста, сообщите мне свой электронный адрес, и я с радостью вышлю Вам свою работу.
С уважением,
Михайлова Людмила Михайловна.

Здравствуйте Людмила Михайловна.
Идея начертания гиперкубов была для меня просто тренировкой для мозгов. Я возвращался к ней еще два раза http://elsper.ru/stereokartinki-giperkuby-stereo-giperkuby/ и http://elsper.ru/2011/02/giperkuby-2/, но за три года уже почти утратил к ней интерес.

К тому же, так как я не рисовал их, а программировал, то мне тоже было нужно разработать универсальный метод построения, с чем я справился. И даже если бы не справился, то все равно думал бы сам, потому, что именно в этом и заключается смысл тренировки. В том, чтобы решить задачу самостоятельно.

Однако, если хотите, я могу сделать ссылку на вашу работу. Интересующиеся смогут ее скачать и прочитать.
Кроме того, вы упомянули трехмерные проекции. Если у вас есть фотографии, то их тоже можно опубликовать. Думаю они заинтересуют всех, кто сюда заходит.
Хотите так?

Здравствуйте, уважаемый Elsper!
Мне очень больно и стыдно признаваться в своей тупости: год назад я купила компьютер, научилась только пользоваться электронной почтой и выходить в интернет, я не могу писать на компьютере математические знаки, формулы, строить таблицы и чертить чертежи — старая я.
До 2011 года я жила в Туркмении. Там же написала свои работы по математике — карандашом, на бумаге, потом эти листы сканировались (т.е. хоть как-то приведены в электронный вид) — это всё, что я могла сделать там, в Туркмении.
С 2011 года я живу на Украине в г.Ивано-Франковске. В квартире я совершенно одна и мне совершенно некому помочь в освоении работы на компьютере.
Вот когда я пишу письмо в своей электронной почте, там на странице есть знак «Прикрепить файл», и я прикрепляю свои работы, — это мне показали. А как вот сейчас, в этом письме, прикрепить свою работу — я не знаю.

Я очень рада: рыская по интернету, я пока увидела — Вы единственный, кто вплотную смог приблизиться к построению горизонтальных проекций трёхмерных проекций n-мерных гиперкубов! Но Ваши проекции правильны только в тех случаях, где n-мерность НЕЧЁТНАЯ. Например, посмотрите на свой ОКТЕРАКТ (восьмое измерение) — в центре чертежа образовался «кружок пустоты», а в данной проекции октеракта центральная точка на чертеже совмещает 16 вершин.
Слава Богу, научили меня пользоваться скайпом. Вот по скайпу я могу показать Вам свои модели трёхмерных проекций четырёхмерного, пятимерного и шестимерного гиперкубов. Если Вы напишете на мою электронную почту свой электронный адрес, то я сообщу Вам свой «логин» для скайпа.
Конечно, я очень хотела бы, чтобы мои работы были хоть как-то опубликованы (для кого я их писала? — для людей!), но я не знаю как это сделать.

Спасибо, что ответили. Всего Вам самого доброго.
С уважением,
Михайлова Людмила Михайловна.

Программа начального многомерного геометрического моделирования NDL_4D
neoethics.narod.ru/n/neo_school/NDL_4D/index.html

Разработка возникла во многом благодаря и Вашей, Elsper, тематической компиляции, за что особое Вам большое спасибо. :)))

Возможно, в случае знакомства, возникнут мобильные конструктивы по дальнейшему развитию идеи освоения многомерных пространства — искренне будем благодарны за любые интересные мысли в данном направлении.

С уважением, Stellari.stA.G

Приятно, что мои работы служат не только мне. )
Правда сейчас меня интересуют совсем другие вопросы.

Источник

kukina_kat

Блог идеальной жены

Как только я стала в состоянии после операции читать лекции, первый же вопрос, который задали студенты:

— Когда вы нам нарисуете 4-мерный куб? Ильяс Абдульхаевич нам обещал!

Я помню, что мои дорогие френды иногда любят минутку математического ликбеза. Поэтому кусочек своей лекции для математиков я напишу и тут. И постараюсь без занудства. Лекцию в каких-то моментах я читаю строже, конечно.

Мы не можем 4-мерный куб потрогать, понюхать, услышать или увидеть. Что же мы можем с ним сделать? Мы можем его себе представить! Потому что наш мозг гораздо более сложная штука, чем наши глаза и руки.

/* Тут же логично представить себе 1-мерный куб, который не что иное как простой отрезок от 0 до 1. */

Так, стоп, а как же рисовать 4-мерный куб? Ведь мы не можем на плоскости нарисовать 4-мерное пространство!
Но ведь 3-мерное пространство мы тоже не рисуем на плоскости, мы рисуем его проекцию на 2-мерную плоскость рисунка. Третью координату (z) мы располагаем под углом, представляя себе, что ось из плоскости рисунка идет «к нам».

Что? Что это вообще? Слышу я всегда шепот с задних парт. Давайте я подробнее объясню, что же это за мешанина линий.
Смотрите сначала на трехмерный куб. Что мы сделали? Мы взяли квадрат и протащили его вдоль третьей оси (z). Это как много-много бумажных квадратов, склеенных в стопку между собой.
С 4-мерным кубом то же самое. Давайте четвертую ось для удобства и для сайнс-фикшн будем называть «ось времени». Нам надо взять обычный трех-мерный куб и протащить его во времени от времени «сейчас» до времени «через час».

У нас есть куб «сейчас». На рисунке он розовый.

Короче, без лирики: нарисовали два одинаковых 3-мерных куба и соединили соответствующие вершины.
Точно так же, как делали с 3-мерным кубом (нарисовали 2 одинаковых 2-мерных куба и соединили вершины).

Чтобы нарисовать 5-мерный куб, вам придется нарисовать две копии 4-мерного куба (4-мерный куб с пятой координатой 0 и 4-мерный куб с пятой координатой 1) и соединить соответствующие вершины ребрами. Правда, на плоскости выйдет такая мешанина ребер, что понять что-либо будет почти невозможно.

Нетрудно так же заметить «верхний» и «нижний».

Их труднее всего заметить, потому что под ногами путаются другие кубы, которые ограничивают гипер-куб по другой спроецированной координате. Но заметьте, что кубы все-таки разные! Вот еще раз картинка, где выделен «куб сейчас» и «куб будущего».

Конечно, можно спроецировать 4-мерный куб в 3-мерное пространство.
Первая возможная пространственная модель понятно как выглядит: надо взять 2 каркаса куба и соединить их соответствующие вершины новым ребром.
У меня такой модели сейчас в наличии нет. На лекции я студентам показываю немного другую 3-мерную модель 4-мерного куба.

Знаете, как куб проецируют на плоскость вот так.
Как будто мы смотрим на куб сверху.

Ближняя грань, понятно, большая. А дальняя грань выглядит поменьше, мы ее видим сквозь ближнюю.

Вот так же можно проецировать 4-мерный куб. Куб сейчас побольше, куб будущего мы видим в отдалении, поэтому он выглядит меньше.

С другой стороны. Со стороны вершины.

Прямо ровно со стороны грани:

Со стороны ребра:

И последний ракурс, несимметричный. Из раздела «ты еще скажи, что я ему между ребер заглядывал».

Ну, а дальше можно придумывать всякое. Например, как бывает развертка 3-мерного куба на плоскость (это как надо вырезать лист бумаги, чтобы при сворачивании получить куб), так же бывает развертка 4-мерного куба в пространство. Это как надо вырезать кусок дерева, чтобы сворачивая его в 4-мерном пространстве мы получили тессеракт.

Можно изучать не просто 4-мерный куб, а вообще n-мерные кубы. Например, правда ли, что радиус сферы, описанной вокруг n-мерного куба меньше, чем длина ребра этого куба? Или вот вопрос попроще: а сколько вершин у n-мерного куба? А сколько ребер (1-мерных граней)?

Для 4-мерного куба все это можно посчитать на трехмерной модели или на рисунке. Но 5-мерный куб мы что-то рисовать не отважились. Так что придется просто представлять все в уме!

Источник

Гиперкубы

ВНИМАНИЕ! Вся изложенная ниже информация скорее всего вообще никогда вам не понадобится и не несет никакого юмора в себе. Читать на свой страх и риск.

Все знают квадрат, куб и линию, но мало кто знает о хексеракте и декеракте. Вот я и решил сделать пост о 11 разных измеренях гиперкубов (от 0 до 10). Вся информация была взята из википедии, но было исключено максимум ненужной информации.

0, 1, 2 и 3 измерение:

Да-да, это обычные наши любимые фигуры: точка, отрезок, квадрат и куб (Соответственно 0, 1, 2 и 3-ех мерные гиперкубы). Я посчитал их скучными и неинтересными и совместил. Теперь приступим к тому, что нам в нашем жалком мирке не представить (По-этому, здесь все 2-у мерные проекции).

В двумерной проекции выглядит плоско (тонкая шутка), но чтобы понять всю суть этого и последующих гиперкубов, гифка:

Именно, все эти гиперкубы имеют равные грани, но находятся они внутри него (в проекции, конечно).
Тессеракт содержит:
16 точек
32 отрезка
24 квадратов
8 кубов

Фигурка побольше. А можете это представить равное кубу в кубе, который в кубе? А это только начало.
Пентеракт содержит:
32 точки
80 отрезков и квадратов
40 кубов

Это уже более позитивно. Содержит в себе:
64 точки
192 отрезка
240 квадратов
160 кубов

Красота. В себе пленила:
128 точки
448 отрезка
672 квадрата
560 куба

А вам это точно надо? Содержит:
256 точки
1024 отрезка
1792 квадрата и куба

Зато ровно.
512 точки
2304 отрезка
4608 квадрата
5376 куба

И, наконец, декеракт (10D):

В себе содержит:
1024 точки
5120 отрезка
11520 квадрата
15360 куба

А теперь представьте.
. все это находится на равном расстоянии друг от друга и внутри друг друга. Ужас, трогает сильнее чем хороры, спать точно кто-то не сможет (если сможет осознать все).

Ах да, если вы дочитали, то имеете право прочесть определение.
Гиперкуб — обобщение куба на случай с произвольным числом измерений.

Я че-то так переволновалась, а потом в обратном порядке до точки пролистала и мне как-то полегче стало.

— Как представить 4-мерное пространство?

— Нужно представить N-мерное и взять N равное 4.

А меня вот куб из интерстеллара захватил.
Я считаю, что идёя подобной развёртки это самое охуенное, что было в кино за последние 28 лет

есть годный видос на тему измерений, типа «как представить 10 измерений», на ютубе

более наглядно чем картинки, которые ломают мозг)

Вы за мной следите? Я только что Куб-2 пересмотрел!

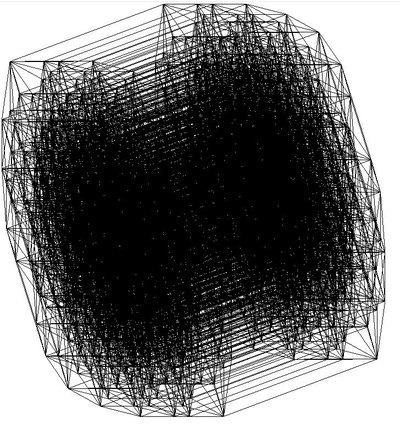
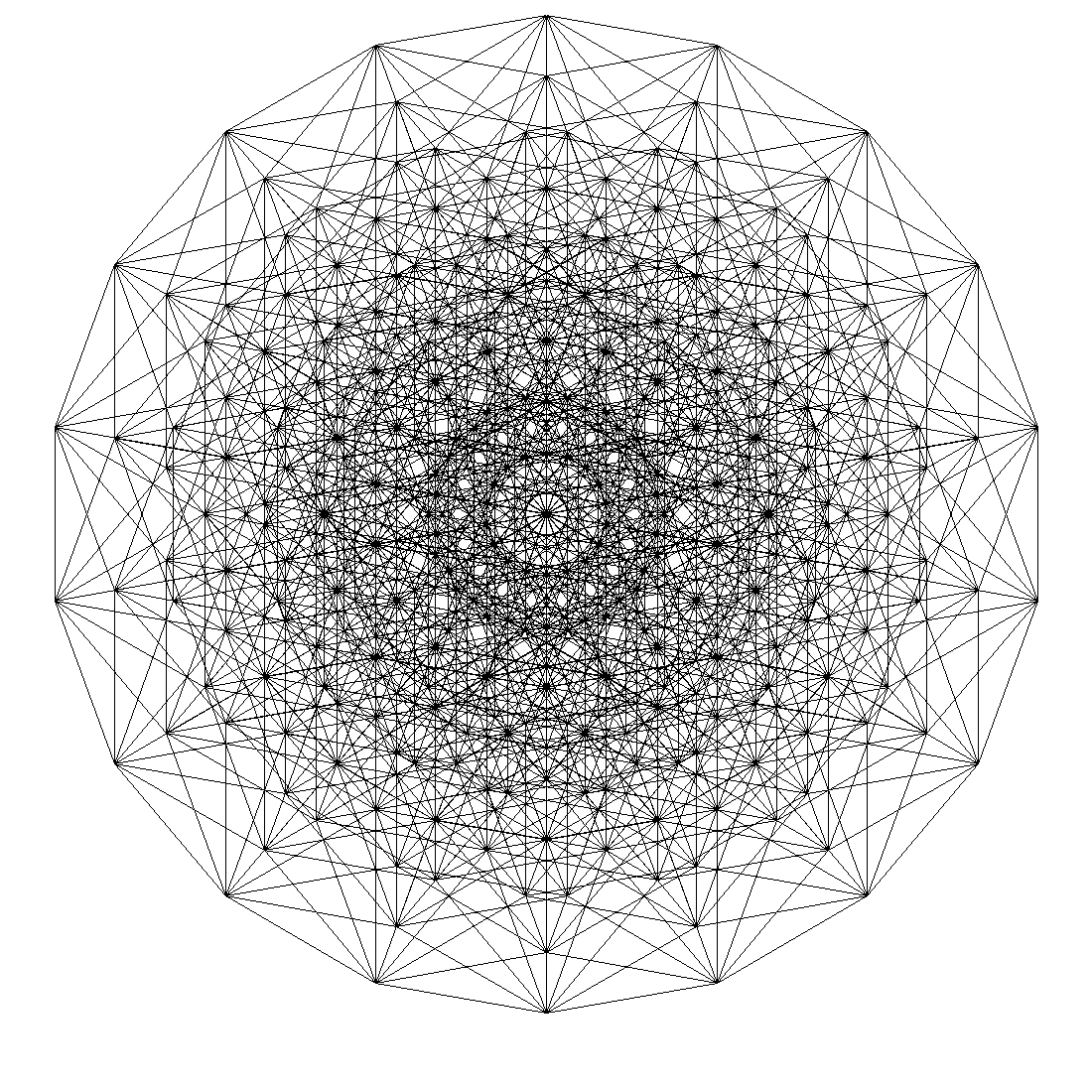
Я как-то развлекался, рисуя кубы. Вот девятимерный и 11-мерный, например:

на мандалу похоже очень

Захватывает! Спасибо за пост! Это как размышлять о бесконечности вселенной.

а почему проекция с увеличением n-мерности все больше походит на круг?

Роберт Хайнлайн
Дом, который построил Тил

Архитектор Квинтус Тил считал своих коллег робкими и неумелыми. Зато ему удалось спроектировать и построить дом в форме тессеракта — из восьми кубов. При этом каждый из них был отдельным помещением: комнатой, кухней, кабинетом и т.д. В ночь перед осмотром готового дома прошло небольшое землетрясение, всего два балла, но дому этого хватило. Он попросту сложился через четвертое измерение в базовую фигуру — куб. Однако все комнаты остались в нем не мешая друг другу и хозяева с архитектором даже походили внутри, правда не без последствий…

Ужас, трогает сильнее чем хороры, спать точно кто-то не сможет (если сможет осознать все).

Мдаааа. Кого-то интересуют машины, кого-то бабы, кого-то трахающиеся насекомые ну или животные, ну пусть даже мертвые. но тут мсье знает толк в извращениях.

О, слушайте такой вопрос.

Сечением отрезка является точка.

Сечением прямоугольника является отрезок.

Сечением куба является прямоугольник.

Верно ли, что сечением 4д куба будет 3д куб?

(Если верно, то что должно быть в качестве секущей в этом случае? 4д- плоскость?)

Ну что за сайт дурноватый. То говорят сделай жест «ок» и наведи его на любой участок неба, представь перспективу. То гиперкубами в тебя мечут. Все мои попытки представить это оканчиваются одним. так, надо уже спать ложиться)

Ты в Анапе-то был, бедолага? Там кинотеатры 12D чуть не каждом углу!

Когда решил рассмотреть поближе

Охуенно пролистал. Спасибо)

Интересно. Кто нибудь обратил внимание что количество точек в каждой фигуре это n степень 2?

От эннеракта как-то не по себе стало

В FEZ на экране загрузки тоже красивая иллюстрация 4d куба была)

Всегда было интересно, вот взять того же больного художника, он начинал видеть эти образы, которые очень похожи на многомерные фигуры. Просто интересная мысль, но может как то мозг человека начинал замечать все эти измерения, или их проекции, но просто мозг не справлялся с такой нагрузкой. Ещё немного и можно написать сюжет к психо-научно-фантастическому фильму.

Представить n-мерный куб с большим n довольно просто. Похож на морского ежа.

Если длина стороны 1, то 2n граней, расстояние между противоположными 1, и 2^n (гораздо больше) вершин, расстояние между самыми отдаленными sqrt(n). То есть в кубе с 10000 измерений 20000 граней и 2^10000 вершин (неизмеримое почти количество), расстояние же между гранями (внутреннее) равно 1, между вершинами (внешнее) до 100. Ну чем не морской еж с иглами-вершинами.

Вот тута чувак очень наглядно разжевывает

Ты случайно не Герыч?

А где шкаф из интерстеллара?

Почему они стремятся к состоянию трёхмерной сферы?

Спасибо за интеллектуальный оргазм

Нууу это вполне себе используется где-нибудь в теории информационной кибениматике, помещаем n-мерный куб со стороной 1 одним углом в 0 прямоугольной координатной сетки и че-то дальше с этим делаем.

Американская фантастика, «Дом который построил Тил.» ( вдруг кто не читал)

Мне после вашего поста херакт полный пришел бл.

Лучше объясни откуда в теории струн столько измерений и нахера

Не путать деградацию с дегенерацией

Но они ведь все трехмерные 🙁

Сложна, йа суда дигродировать прехожу

О клиентах и геометрии

Пришла сегодня тетка напечатать фотографии. Отправляет на почту, рассказывает пожелания к печати:

— Мне, пожалуйста, все эти фото размером 9х9 сантиметров.

— У вас фотографии вытянутые. Чтобы нам из них получить квадрат, нужно либо что-то обрезать, либо оставлять белые поля сверху и снизу.

Ловлю решительно непонимающий взгляд и фразу:

— Нет, обрезать ничего не нужно. И полей никаких не нужно. Печатайте как есть, мне нужны квадраты 9х9 сантиметров!

Что ж, и такое бывало. Объясняю глубже.

После этого многие непонимающие обычно вникают. Глубокомысленно задумываются и уходят подбирать другие фотографии, или показывают, где можно срезать лишнее, дабы получить искомый квадрат.

Но эта тетя не вникла ни капельки:

— В смысле невозможно? Вы что, не в состоянии напечатать квадраты 9х9?

— В состоянии, но результат вас не устроит, а материал будет потрачен.

Предпринимаю последнюю попытку что-то объяснить. Открываю Word, закидываю туда первую попавшуюся из ее фоток, и принудительно сминаю ширину (люди становятся похожими на длинных и тонких яйцеголовых пришельцев). Поворачиваю монитор и показываю результат.

— Это третий вариант напечатать квадрат из ваших фото. Вам нравится?

— Вы что, издеваетесь что ли?

— Я вас просила нормально сделать! А вы!! Ну и профессионал! Я пойду к другим, где разберутся, что мне нужно!

С этими словами она покинула наше заведение, и этим очень нас порадовала. Остается только посочувствовать тем, к кому она пошла.

Источник