Что используют для вычисления элементов внешнего ориентирования модели
Элементы внешнего (геодезического) ориентирования модели
Элементами внешнего ориентирования модели называют величины, определяющие масштаб фотограмметрической модели и се положение в пространстве относительно системы координат местности.
 |
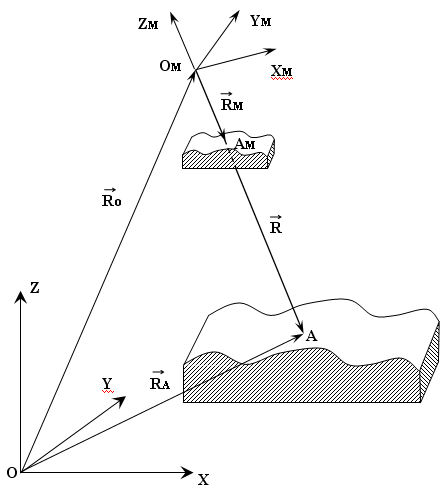
| Рис. 10.3. Элементы внешнего ориентирования модели |
Внешнее ориентирование фотограмметрической модели по опорным точкам
Поскольку системы отсчета угловых элементов внешнего ориентирования аэроснимка (рис. 3.7) и модели (рис. 10.3) полностью идентичны, для установления связи между координатами точек в системах OrXrYrZr и OXYZ можно воспользоваться следующими формулами, вытекающими из (3.1) с учетом различия их масштабов:
| хг | х0 | «, | а, | а3 | X | хп | AX’J | |||||
| Yr | = | у, | + tx | ft, | Ь 2 | ft, | X | Y | = | у, | + | лу; |
| zr | z» | с, | С 2 | с ъ | Z | z0 | AZ’r\ |
Пусть имеются приближенные значения элементов внешнего ориентирования модели Xq, Y’q, Zq, ^о» Ло> 9(ь *о и требуется лишь отыскать поправки 5Xq, 5Yq, 5Zq, 5£, 5r|, 50, 5/ к ним. С-этой целью приведем формулы (10.4) к линейному виду разложением в ряд Тейлора и представим их в форме уравнений поправок, составляемых для опорных точек с известными координатами Хг ,УГ и Zr
Zx= *o + ДХ’г-Хг, /у= Уо + AYY-Yn z 2 = Z o + AZ’r-Zr,
a x> by> Cz> •> 8x> Јy> Sz
частные производные от функций (10.4) но соответствующим неизвестным; АХ’п AY’r, AZ’r— приращения координат, найденных по формулам (10.4), по приближенным элементам внешнего ориентирования модели.
При наличии избыточных измерений задачу решают путем последовательных приближений, под условием [pvv] = min. С этой целью для всех опорных точек, включенных в фотограмметрическую модель,
составляют уравнения поправок (10.5) и систему нормальных уравнений седьмого порядка, из решения которой определяют поправки к приближенным (начальным) значениям неизвестных. Этими поправками уточняют приближенные значения неизвестных и выполняют второе приближение. Так продолжают до тех пор, пока поправки к неизвестным не окажутся меньше установленного допуска. Критерием сходимости итерационного процесса служат расхождения геодезических координат опорных точек от их значений, найденных по фомулам (10.4).
определяемыми по формулам (9.34) и (9.35). Очевидно, что произведения этих матриц определяют взаимное положение координатных систем S\xyz и S2xyz относительно системы координат местности OvXTYxZT\
^лЮлХл = A W X АхлШлХл
J a iX i a2o) 2X2
Внешнее ориентирование модели. Элементы внешнего ориентирования модели
7. Внешнее ориентирование модели. Элементы внешнего ориентирования модели
 |
Рис. 1
Векторы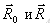 
определяют положение начала системы координат модели ОМХМYMZM и точки А местности относительно начала системы координат объекта OXYZ.
Векторы 
определяют соответственно положение точек АМ и А относительно системы координат фотограмметрической модели.
Из рис. 1 следует, что
. ( 1)
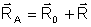
Векторы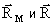 
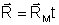
коллинеарны, поэтому
; ( 2)
где t – знаменатель масштаба модели.
С учетом ( 2) выражение ( 1) имеет вид:
В координатной форме выражение ( 3) имеет вид:
; ( 4)
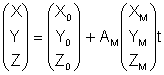
В выражениях ( 4) и ( 5):
X, Y, Z – координаты точки объекта в системе координат объекта;
АМ – матрица преобразования координат, элементы aij которой являются функциями углов wМ, aМ, ÀМ, определяющих ориентацию системы координат модели относительно системы координат объекта;
t – знаменатель масштаба модели.
7 параметров: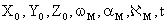 
— называют элементами внешнего ориентирования модели.
8. Определение элементов внешнего ориентирования модели по опорным точкам
Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения ( 7.5), которые представим в виде:
. ( 1)
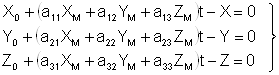
Каждая планово-высотная опорная точка (X,Y,Z) позволяет составить 3 уравнения ( 1), в которых неизвестными являются 7 элементов внешнего ориентирования модели. Каждая плановая опорная точка (X,Y) позволяет составить два первых уравнения из выражения ( 1), а каждая высотная опорная точка (Z) – третье уравнение из выражения ( 1).
Для определения элементов внешнего ориентирования модели необходимо составить систему не менее чем из 7 уравнений. Очевидно, что для этого необходимо иметь не менее двух планово-высотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.
Так как уравнения ( 1) не линейны, их приводят к линейному виду и переходят к уравнениям поправок.
. ( 2)
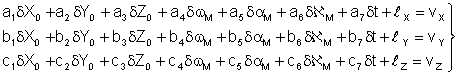
В уравнении поправок:
ai, bi, ci – частные производные от уравнений ( 1) по соответствующим переменным ;
Полученную таким образом систему уравнений поправок решают методом последовательных приближений. Если количество уравнений поправок в системе больше семи, то ее решают по методу наименьших квадратов (под условием V T PV=min).
9. Определение элементов внешнего ориентирования снимков стереопары
По элементам внешнего ориентирования модели и элементам взаимного ориентирования можно определить элементы внешнего ориентирования снимков стереопары.
Линейные элементы внешнего ориентирования снимков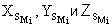 
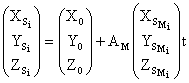
определяют по формулам:
; ( 1)
в которых 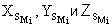— координаты центра проекции i-го снимка стереопары в системе координат модели.
Угловые элементы внешнего ориентирования снимков wi, ai, Ài определяют в следующей последовательности:
1. Сначала получают матрицу преобразования координат i-го снимка
; ( 2)
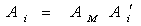
АМ – матрица, в которой элементы aij вычисляют по угловым элементам внешнего ориентирования модели wМ, aМ, ÀМ ;
Ai’ – матрица, в которой элементы aij вычисляют по угловым элементам взаимного ориентирования i-го снимка wi’, ai’, Ài’.
2. Затем по элементам aij матрицы Ai вычисляют угловые элементы внешнего ориентирования i-го снимка стереопары:
.
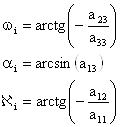
10. Точность определения координат точек объекта по стереопаре снимков
Для предрасчета точности определения координат точек местности по стереопаре аэрофотоснимков, учитывая, что углы наклона снимков не превышают 1°- 3°, а базис фотографирования практически горизонтален, воспользуемся формулами связи координат точек местности и координат их изображений на стереопаре снимков идеального случая съемки ( 2.4):
. ( 2.4)
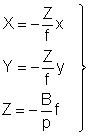
Сначала получим среднюю квадратическую ошибку определения высоты точки Z местности. Для этого продифференцируем третью формулу выражения (1.8.4) по аргументу р.
.
 |
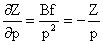
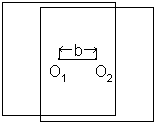Заменим величину р на b – базис в масштабе снимка.
На рис.1 О1и О2 – главные точки снимка.
В результате получим
.
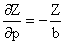
Перейдя к средним квадратическим ошибкам получим формулу:
. ( 1)
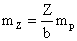
Для получения средних квадратических ошибок определения координат Х и Y точки местности продифференцируем первые две формулы выражения (1.8.4) по аргументам x, y, Z и перейдем к средним квадратическим ошибкам.
В результате получим
. ( 2)
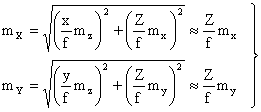
В качестве примера вычислим величины mX, mY и mZ точек местности, определенных по стереопаре снимков масштаба 1:5000, полученной АФА с f =150 мм и форматом кадра 23х23 см, с продольным перекрытием 60%.
Будем считать, что на стереопаре снимков точки были измерены с ошибками
.
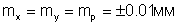
В этом случае высота фотографирования
;
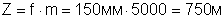
а базис фотографирования в масштабе снимка
.
Средние квадратические ошибки определения координат точки местности, вычисленные по формулам ( 1) и ( 2) будут равны:
.
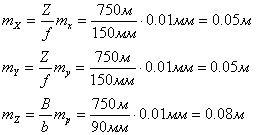
Внешнее ориентирование модели. Элементы внешнего ориентирования модели.
 |
Векторы 
определяют положение начала системы координат модели ОМХМYMZM и точки А местности относительно начала системы координат объекта OXYZ.
Векторы 
определяют соответственно положение точек АМ и А относительно системы координат фотограмметрической модели.
Из рис.1.13.1 следует, что
. (1.13.1)
Векторы 
коллинеарные, поэтому
; (1.13.2)
где t – знаменатель масштаба модели.
С учетом (1.13.2) выражение (1.13.1) имеет вид:
; (1.13.3)
В координатной форме выражение (1.13.3) имеет вид:
; (1.13.4)
. (1.13.5)
В выражениях (1.13.4) и (1.13.5):
X, Y, Z – координаты точки объекта в системе координат объекта;
АМ – матрица преобразования координат, элементы aij которой являются функциями углов wМ, aМ, ÀМ, определяющих ориентацию системы координат модели относительно системы координат объекта;
t – знаменатель масштаба модели.
7 параметров: 
— называют элементами внешнего ориентирования модели.
1.14 Определение элементов внешнего ориентирования модели по опорным точкам.
Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения (1.13.5), которые представим в виде:
. (1.14.1)
Каждая планово-высотная опорная точка (X,Y,Z) позволяет составить 3 уравнения (1.14.1), в которых неизвестными являются 7 элементов внешнего ориентирования модели. Каждая плановая опорная точка (X,Y) позволяет составить два первых уравнения из выражения (1.14.1), а каждая высотная опорная точка (Z) – третье уравнение из выражения (1.14.1).
Для определения элементов внешнего ориентирования модели необходимо составить систему не менее чем из 7 уравнений. Очевидно, что для этого необходимо иметь не менее двух планово-высотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.
Так как уравнения (1.14.1) не линейны, их приводят к линейному виду и переходят к уравнениям поправок.
. (1.14.2)
В уравнении поправок:
ai, bi, ci – частные производные от уравнений (1.14.1) по соответствующим переменным ;
Значения коэффициентов уравнений поправок ai, bi, ci вычисляют по известным значениям координат ХМ, YM, ZM и X, Y, Z и приближенным значениям неизвестных. Значения свободных членов ℓX, ℓY, ℓZ вычисляют таким же образом по формулам (1.14.1).
Полученную таким образом систему уравнений поправок решают методом последовательных приближений. Если количество уравнений поправок в системе больше семи, то ее решают по методу наименьших квадратов (под условием V T PV=min).
1.15 Определение элементов внешнего ориентирования снимков стереопары.
По элементам внешнего ориентирования модели и элементам взаимного ориентирования можно определить элементы внешнего ориентирования снимков стереопары.
Линейные элементы внешнего ориентирования снимков 
определяют по формулам:
; (1.15.1)
в которых — координаты центра проекции i-го снимка стереопары в системе координат модели.
Угловые элементы внешнего ориентирования снимков wi, ai, Ài определяют в следующей последовательности:
1. Сначала получают матрицу преобразования координат i-го снимка
; (1.15.2)
АМ – матрица, в которой элементы aij вычисляют по угловым элементам внешнего ориентирования модели wМ, aМ, ÀМ ;
Ai’ – матрица, в которой элементы aij вычисляют по угловым элементам взаимного ориентирования i-го снимка wi’, ai’, Ài’.
2. Затем по элементам aij матрицы Ai вычисляют угловые элементы внешнего ориентирования i-го снимка стереопары:
.
Определение элементов внешнего ориентирования модели по опорным точкам
Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения (2.8.5), которые представим в виде:
(2.9.1)
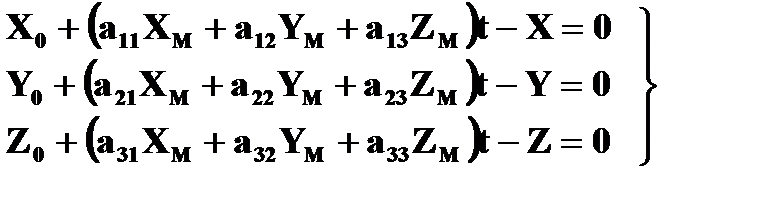
Каждая планово-высотная опорная точка (X,Y,Z) позволяет составить 3 уравнения (2.9.1), в которых неизвестными являются 7 элементов внешнего ориентирования модели. Каждая плановая опорная точка (X,Y) позволяет составить два первых уравнения из выражения (2.9.1), а каждая высотная опорная точка (Z) – третье уравнение из выражения (2.9.1).
Для определения элементов внешнего ориентирования модели необходимо составить систему не менее чем из 7 уравнений. Очевидно, что для этого необходимо иметь не менее двух планово-высотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.
В случае, если в полете с помощью спутниковых навигационных систем были определены координаты центров проекций снимков, то они могут быть использованы в качестве опорных точек.
Так как уравнения (2.9.1) не линейны, их приводят к линейному виду и переходят к уравнениям поправок.
(2.9.2)
В уравнении поправок:
ai, bi, ci – частные производные от уравнений (2.9.1) по соответствующим переменным ;
Значения коэффициентов уравнений поправок ai, bi, ciвычисляют по известным значениям координат ХМ, YM, ZM и X, Y, Z и приближенным значениям неизвестных. Значения свободных членов ℓX, ℓY, ℓZ вычисляют таким же образом по формулам (2.9.1).
Полученную таким образом систему уравнений поправок решают методом последовательных приближений. Если количество уравнений поправок в системе больше семи, ее решают по методу наименьших квадратов (под условием V T PV=min).
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)
Внешнее ориентирование модели. Элементы внешнего ориентирования модели
Векторы 
определяют положение начала системы координат модели ОМХМYMZM и точки А местности относительно начала системы координат объекта OXYZ.
Векторы RM=OMAM и R=OMA определяют соответственно положение точек АМ и А относительно системы координат фотограмметрической модели OM.
Из рис.2.8.1 следует, что
(2.8.1)
Векторы 
коллинеарны, поэтому
, (2.8.2)
где t – знаменатель масштаба модели.
С учетом (2.8.2) выражение (2.8.1) имеет вид:
(2.8.3)
В координатной форме выражение (2.8.3) имеет вид:
(2.8.4)
(2.8.5)
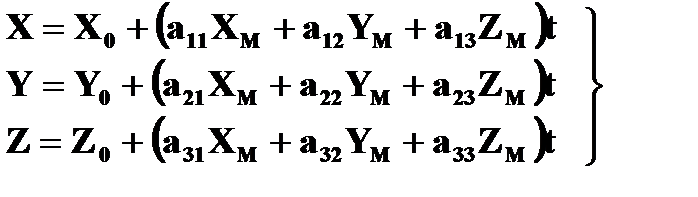
В выражениях (2.8.4) и (2.8.5):
X, Y, Z – координаты точки объекта в системе координат объекта;
АМ – матрица преобразования координат, элементы aij которой являются функциями углов wМ, aМ, ÀМ, определяющих ориентацию системы координат модели относительно системы координат объекта;
t – знаменатель масштаба модели.
7 параметров: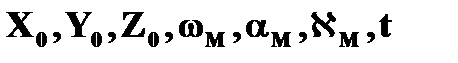 
— называют элементами внешнего ориентирования модели.
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)