Что лежит в основе октаэдра

Октаэдр и площадь полной его поверхности: описание, формулы, примеры

Содержание:

Существует несколько способов определить площадь поверхности октаэдра. Он представляет собой один из пяти правильных многоугольников или так называемых Платоновых тел. Имеет восемь одинаковых граней (поверхностей) в виде равносторонних треугольников, к каждой из его вершин прилагается по четыре грани. Рассмотрим, что собой представляет тело, где встречается в природе, как вычисляется его площадь и объём.

Что такое октаэдр

Свойства октаэдра

Математические характеристики тела

Как вычислить площадь поверхности октаэдра

Площадь октаэдра равна сумме площадей составляющих его треугольников:

Здесь S_треуг – площадь треугольника.

После подстановки значения получится требуемый результат.

Если известна длина ребра, придётся вычислить площадь треугольников.

Подставляем значение в первое выражение:

Упрощаем: после сокращения дроби на четыре получается формула площади поверхности октаэдра:

2. S = 8 * S_треуг = 2 \sqrt <3>a^2.

Существует ещё один способ проведения вычислений. Он менее точный чем предыдущие, однако позволяет обойтись без калькулятора. При приблизительном подсчёте 2 \sqrt <3>равняется 3,464 или 3,46.

Здесь a – длина стороны треугольника (равны).

Для примера, имеется фигура октаэдр с длиной стороны 5 см.

S=2\sqrt <3>a^2=2*\sqrt <3>*5^2=2*\sqrt <3>*25=50\sqrt <3>\approx 86,6 см.

Как вычислить объём правильного октаэдра

Объём показывает размер внутреннего пространства геометрического тела. Объем правильного октаэдра вычисляется, если знаете длину ребра геометрического тела, по формуле:

После проведения приблизительных расчётов \frac<\sqrt 2> <3>\approx 0,47 формула принимает следующий вид :

Рассчитаем двумя методами на примере правильного многоугольника с гранью, равной 5 см:

V= 0,47 * a^3 = 0,47*125 \approx 58,93

Значения совпали, во втором случае нужно выполнять гораздо меньше операций. Подходит он только, если не требуется исключительная точность – при округлении до 4-5 знаков после запятой точность снизится.

Развёртка

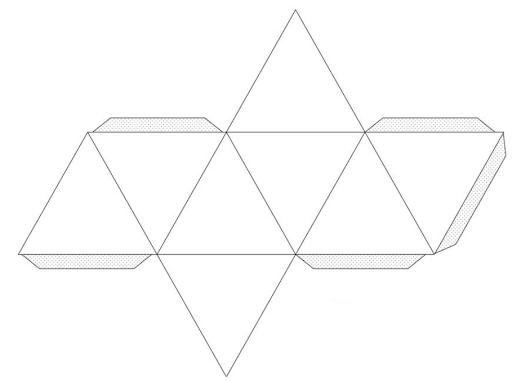
Октаэдр, как большинство гомерических тел, имеет развёртку поверхности – это плоская фигура, полученная путём совмещения поверхности модели с одной плоскостью без пересечения либо наложения граней друг на друга.

Рисунок развёртки октаэдра.

В природе насчитывается 11 разновидностей развёртки октаэдра, позволяющих создать его модель из бумаги или картона. Наиболее распространённая выглядит как восемь одинаковых треугольников. Шесть из них размещено в ряд, к третьему и четвёртому основаниям прилегает ещё по одному, их вершины направлены в противоположные стороны.

Источник

Октаэдр

Октаэдр имеет следующие характеристики:

Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.

Математические характеристики октаэдра

Октаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы октаэдра определяется по формуле:

Сфера может быть вписана внутрь октаэдра.

Радиус вписанной сферы октаэдра определяется по формуле:

Площадь поверхности октаэдра

Для наглядности, площадь поверхности октаэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон октаэдра (это площадь правильного треугольника) умноженной на 8. Либо воспользоваться формулой:

Объем октаэдра определяется по следующей формуле:

Октаэдр можно представить в виде двух правильных пирамид с четырехугольным основанием, соединенных друг с другом через это основание.

Вариант развертки

Древнегреческий философ Платон ассоциировал октаэдр с «земным» элементом воздух, поэтому для построения модели этого правильного многогранника мы выбрали серый цвет.

Заметим, что это не единственный вариант развертки.

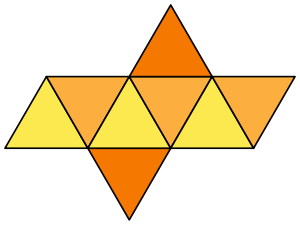
Классический вариант раскраски предполагает окраску октаэдра четырьмя различными цветами, причем таким образом, что каждая грань имеет свой цвет отличный от соседней и только противоположные не соприкасающиеся друг с другом грани окрашиваются в одинаковые цвета.

Вариант окраски представлен на рисунке. Вы можете скачать развертку с соответствующей раскраской граней.

Видео. Октаэдр из набора «Волшебные грани»

Вы можете изготовить модель октаэдра воспользовавшись деталями для сборки из набора «Волшебные грани».

Сборка многогранника из набора:

Подробная сборка от Алексея Жигулева (youtube-канал Оригами)

вращение готового многогранника:

Видео. Вращение правильных многогранников

Популярное

Какое из известных нам геометрических тел обладает наибольшей прочностью? Наиболее устойчиво к внешним деформациям?

Александрийский маяк — одно из 7 чудес света, был построен в III веке до н. э. в египетском городе Александрия, чтобы корабли могли благополучно миновать рифы на пути в александрийскую.

(головоломка «звезда») Состоит из шести симметричных брусочков сложной формы, соединенных в форме многогранной звезды. Задача заключается в том, чтобы разъединить фигуру на.

Основатели города Мирный, находящегося в Архангельской области разместили на флаге и гербе своего города многогранник – «Большой додекаэдр».

В этой статье мы постараемся рассказать можно ли наборы «волшебные грани» отнести к разновидности оригами. Как одну и ту же геометрическую фигуру можно получить, используя детали из.

Интересный лайфхак, прислала наша читательница из Республики Беларусь.

Источник

Содержание

Правильный октаэдр

Размеры

Если длина ребра правильного октаэдра равна а, то радиус ограниченного сфера (тот, который касается октаэдра во всех вершинах)

и радиус вписанной сферы (касательная к каждой из граней октаэдра)

в то время как средний радиус, который касается середины каждого края, равен

Ортогональные проекции

В октаэдр имеет четыре специальных ортогональные проекции, по центру, на ребре, вершине, грани и по нормали к грани. Второй и третий соответствуют букве B₂ и А₂ Самолеты Кокстера.

Ортогональные проекции

В центре	Край	Лицо Нормальный	Вершина	Лицо
Изображение
Проективный симметрия	[2]	[2]	[4]	[6]

Сферическая черепица

Октаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются как дуги окружности на плоскость.

Декартовы координаты

Октаэдр с длиной ребра √ 2 может быть размещен с центром в начале координат и вершинами на осях координат; то Декартовы координаты вершин тогда

( ±1, 0, 0 ); ( 0, ±1, 0 ); ( 0, 0, ±1 ).

Площадь и объем

Площадь поверхности А и объем V правильного октаэдра реберной длины а находятся:

Таким образом, объем в четыре раза больше, чем у обычного тетраэдр с одинаковой длиной ребра, а площадь поверхности в два раза (потому что у нас 8, а не 4 треугольника).

Если октаэдр был растянут так, что он подчиняется уравнению

формулы для площади поверхности и объема расширяются, чтобы стать

Кроме того, тензор инерции вытянутого октаэдра равен

Они сводятся к уравнениям для правильного октаэдра, когда

Геометрические отношения

Октаэдр уникален среди Платоновых тел тем, что в каждой вершине встречается четное число граней. Следовательно, это единственный член этой группы, у которого есть зеркальные плоскости, которые не проходят ни через одну из граней.

Используя стандартную номенклатуру для Твердые тела Джонсона, октаэдр назовем квадратная бипирамида. Усечение двух противоположных вершин приводит к квадратный двустворчатый.

Октаэдр 4-связный, что означает, что нужно удалить четыре вершины, чтобы разъединить оставшиеся вершины. Это один из четырех 4-х соединенных симплициальный хорошо покрытый многогранники, что означает, что все максимальные независимые множества его вершин имеют одинаковый размер. Остальные три многогранника с этим свойством являются пятиугольная дипирамида, то курносый дисфеноид, и неправильный многогранник с 12 вершинами и 20 треугольными гранями. [1]

Октаэдр также может быть сгенерирован как трехмерный суперэллипсоид со всеми значениями, установленными на 1.

Равномерная окраска и симметрия

Есть 3 равномерные раскраски октаэдра, названного цветами треугольных граней, окружающих каждую вершину: 1212, 1112, 1111.

Октаэдр группа симметрии это O_час, порядка 48, трехмерное гипероктаэдрическая группа. Эта группа подгруппы включить D_3D (порядок 12) группа симметрии треугольного антипризма; D_4ч (порядок 16) группа симметрии квадрата бипирамида; и т_d (порядок 24) группа симметрии выпрямленный тетраэдр. Эти симметрии можно подчеркнуть разной окраской лиц.

Он имеет одиннадцать аранжировок сети.

Двойной

Огранка

Униформа тетрагемигексаэдр это тетраэдрическая симметрия огранка правильного октаэдра, разделяющего край и расположение вершин. У него четыре треугольных грани и три центральных квадрата.

Неправильные октаэдры

Следующие многогранники комбинаторно эквивалентны правильному многограннику. Все они имеют шесть вершин, восемь треугольных граней и двенадцать ребер, которые однозначно соответствуют характеристикам правильного октаэдра.

Другие выпуклые октаэдры

В более общем смысле, октаэдром может быть любой многогранник с восемью гранями. Правильный октаэдр имеет 6 вершин и 12 ребер, минимум для октаэдра; неправильные октаэдры могут иметь до 12 вершин и 18 ребер. [2] Есть 257 топологически различных выпуклый октаэдры, исключая зеркальные изображения. Более конкретно, существует 2, 11, 42, 74, 76, 38, 14 для октаэдров с 6–12 вершинами соответственно. [3] [4] (Два многогранника являются «топологически разными», если они имеют внутренне различное расположение граней и вершин, так что невозможно преобразовать один в другой, просто изменяя длину ребер или углы между ребрами или гранями.)

Некоторые более известные неправильные октаэдры включают следующее:

Октаэдра в физическом мире

Октаэдра в природе

Октаэдры в искусстве и культуре

Тетраэдрическая ферма

Каркас из повторяющихся тетраэдров и октаэдров был изобретен Бакминстер Фуллер в 1950-х годах, известный как космический каркас, обычно считается самой сильной структурой для сопротивления консоль стрессы.

Связанные многогранники

Правильный октаэдр можно дополнить до тетраэдр добавлением 4 тетраэдров на чередующихся гранях. Добавление тетраэдров ко всем 8 граням создает звездчатый октаэдр.

Это также один из простейших примеров гиперсимплекс, многогранник, образованный некоторыми пересечениями гиперкуб с гиперплоскость.

Октаэдр топологически связан как часть последовательности правильных многогранников с Символы Шлефли <3,п>, переходя в гиперболическая плоскость.

*п32 изменения симметрии правильных мозаик: <3,п>
Сферический				Евклид.	Компактный гипер.		Paraco.	Некомпактный гиперболический
3.3	3 3	3 4	3 5	3 6	3 7	3 8	3 ∞	3 12i	3 9i	3 6i	3 3i

Тетратетраэдр

Сравните эту последовательность усечения между тетраэдром и его двойником:

*п32 орбифолдные симметрии квазирегулярных мозаик: (3.п) 2
Строительство	Сферический			Евклидово	Гиперболический
	*332	*432	*532	*632	*732	*832.	*∞32
Квазирегулярный цифры
Вершина	(3.3) 2	(3.4) 2	(3.5) 2	(3.6) 2	(3.7) 2	(3.8) 2	(3.∞) 2

Тригональная антипризма

Как тригональная антипризмаоктаэдр относится к семейству гексагональной диэдральной симметрии.

Источник

Октаэдр

Октаэдр
Тип	Правильный многогранник
Грань	треугольник
Граней
Рёбер
Вершин
Граней при вершине
Длина ребра
Площадь поверхности
Объём
Радиус описанной сферы
Радиус вписанной сферы
Точечная группа симметрии	Октаэдрическая (Oh)
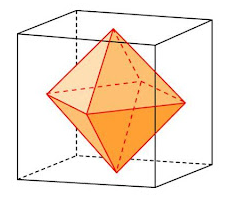
Двойственный многогранник	Куб

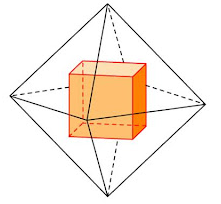
Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.

Если длина ребра октаэдра равна а, то площадь его полной поверхности (S) и объём октаэдра (V) вычисляются по формулам:

Радиус сферы, описанной вокруг октаэдра, равен:

,

радиус вписанной в октаэдр сферы может быть вычислен по формуле:

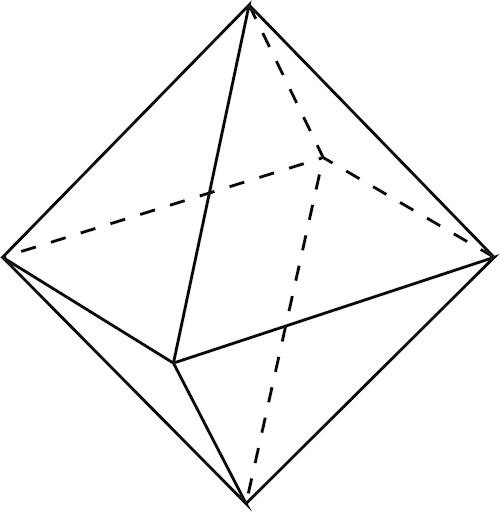
Правильный октаэдр имеет симметрию O_h, совпадающую с симметрией куба.

Октаэдр в природе

Источники

Полезное

Смотреть что такое «Октаэдр» в других словарях:

ОКТАЭДР — геометр. тело, ограниченное 8 равносторонними треугольниками. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. ОКТАЭДР греч. oktaedros, от okto, восемь, и hedra, основание. Восьмигранник. Объяснение 25000… … Словарь иностранных слов русского языка

октаэдр — многогранник, восьмигранник Словарь русских синонимов. октаэдр сущ., кол во синонимов: 2 • восьмигранник (2) • … Словарь синонимов

октаэдр — а, м. octaèdre m. < octaedron. Правильный восьмигранник, тело, ограниченное восемью треугольниками. СИС 1954. В октаедрах. Витт Пром. хим. 1848 2 187. Из кристаллических форм <металлов> преобладают кубы и в особенности октаэдры. МБ 1900… … Исторический словарь галлицизмов русского языка

ОКТАЭДР — (от греческого okto восемь и hedra сиденье, плоскость, грань), один из пяти типов правильных многогранников; имеет 8 граней (треугольных), 12 рёбер, 6 вершин (в каждой сходятся 4 ребра) … Современная энциклопедия

ОКТАЭДР — (от греч. okto восемь и hedra грань) один из пяти типов правильных многогранников; имеет 8 граней (треугольных), 12 ребер, 6 вершин (в каждой сходятся 4 ребра) … Большой Энциклопедический словарь

ОКТАЭДР — ОКТАЭДР, октаэдра, муж. (от греч. okto восемь и hedra основание). Правильный восьмигранник, ограниченный восьмью правильными треугольниками. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

октаэдр — одна из форм структурной организации вирусов (бактериофагов), вирионы которых представляют собой правильный многогранник с 8 гранями и 6 вершинами. (Источник: «Микробиология: словарь терминов», Фирсов Н.Н., М: Дрофа, 2006 г.) … Словарь микробиологии

ОКТАЭДР — [όχτώ (ξкто) восемь; έδρα (γедра) грань] замкнутый восьмигранник с гранями в виде правильных треугольников. Символ О. <111>. См. Формы кристаллов простые высшей (кубической) сингонии.… … Геологическая энциклопедия

октаэдр — — [Англо русский геммологический словарь. Красноярск, КрасБерри. 2007.] Тематики геммология и ювелирное производство EN octahedron … Справочник технического переводчика

Октаэдр — (от греческого okto восемь и hedra сиденье, плоскость, грань), один из пяти типов правильных многогранников; имеет 8 граней (треугольных), 12 рёбер, 6 вершин (в каждой сходятся 4 ребра). … Иллюстрированный энциклопедический словарь

Источник

• ← Страховка автомобиля через сбербанк
• 404 регион россии на машине →

Многогранники
Правильные (Платоновы тела)	Трёхмерные Правильный тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр Четырёхмерные 6 правильных многогранников Большей размерности N-мерный куб • N-мерный октаэдр • N-мерный тетраэдр
Звёздчатый додекаэдр • Звёздчатый икосододекаэдр • Звёздчатый икосаэдр • Звёздчатый многогранник • Звёздчатый октаэдр
Выпуклые	Архимедовы тела Кубооктаэдр • Икосододекаэдр • Усечённый тетраэдр • Усечённый октаэдр • Усечённый икосаэдр • Усечённый куб • Усечённый додекаэдр • Ромбокубоктаэдр • Ромбоикосододекаэдр • Ромбоусечённый кубоктаэдр • Ромбоусечённый икосододекаэдр • Курносый куб • Курносый додекаэдр • Усечённый кубооктаэдр • Усечённый икосододекаэдр • Правильная призма • Антипризма Каталановы тела Ромбододекаэдр • Ромботриаконтаэдр • Триакистетраэдр • Тетракисгексаэдр • Пентакисдодекаэдр • Триакисоктаэдр • Триакисикосаэдр • Дельтоидальный икоситетраэдр • Дельтоидальный гексеконтаэдр •Пентагональный икоситетраэдр • Пентагональный гексеконтаэдр • Дисдакисдодекаэдр • Дисдакистриаконтаэдр Без полной пространственной симметрии Пирамида • Призма • Бипирамида • Антипризма • Зоноэдр • Параллелепипед • Ромбоэдр •Призматоид• Усечённая пирамида• Пентагондодекаэдр • Параллелоэдр
Формулы, теоремы, теории