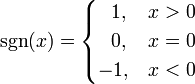что показывает функция сигнум в логистической регрессии

Функция sign(x)

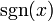
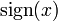
Функция (другое обозначение: , читается: «сигнум», от лат. signum — знак) определяется следующим образом:

Свойства функции

Полезное

Смотреть что такое «Функция sign(x)» в других словарях:

функция mod_osso — Новое функциональное средство, введенное в Oracle9iAS Release 2. Оно является расширением Oracle HTTP Server, которое позволяет HTTP серверу стать партнерским приложением (см. Partner Applications) для SSO (см. Single Sign On, SSO). Приложения,… … Справочник технического переводчика

Функция ошибок — График функции ошибок В математике функция ошибок (функция Лапласа) это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных ур … Википедия

Функция Ляпунова — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. В теории обыкновенных дифференциальных уравнений, функция Ляпунова является скалярной функцией, которая… … Википедия

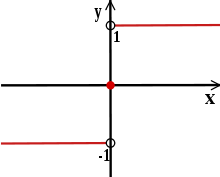
Функция sgn(x) — График функции y = sgn x Функция (другое обозначение: ), читается «сигнум» (от лат. signum знак) кусочно постоянная функция, определённа … Википедия

Функция Радемахера — Графики функций Радемахера с Функция Радемахера кусочно постоянная периодическая функция, принимающая только два значения 1 и −1 на всей обл … Википедия

Однородная функция — степени числовая функция такая, что для любого и выполняется равенство: причём называют порядком однородности. Различают также положительно однородные функции, для которых равенство … Википедия

Источник

Введение в логистическую регрессию

Дата публикации Jan 22, 2019

Введение

В этом блоге мы обсудим основные концепции логистической регрессии и какие проблемы она может помочь нам решить.

Какие типы логистической регрессии

Логистическая регрессия

Мы можем назвать логистическую регрессию моделью линейной регрессии, но в логистической регрессии используется более сложная функция стоимости, эту функцию стоимости можно определить какСигмовидная функцияИли также известный как «логистическая функция» вместо линейной функции.

Гипотеза логистической регрессии стремится ограничить функцию стоимости между 0 и 1. Поэтому линейные функции не могут представить ее, поскольку она может иметь значение больше 1 или меньше 0, что невозможно в соответствии с гипотезой логистической регрессии.

Что такое сигмовидная функция?

Чтобы отобразить прогнозируемые значения на вероятности, мы используем функцию Sigmoid. Функция отображает любое действительное значение в другое значение между 0 и 1. В машинном обучении мы используем сигмоид, чтобы отобразить предсказания на вероятности.

Гипотеза Представление

Когда используешьлинейная регрессиямы использовали формулу гипотезы, т.е.

Для логистической регрессии мы собираемся немного ее изменить, т.е.

Мы ожидали, что наша гипотеза даст значения от 0 до 1.

Граница решения

Мы ожидаем, что наш классификатор даст нам набор выходных данных или классов, основанных на вероятности, когда мы передадим входные данные через функцию прогнозирования и вернем оценку вероятности между 0 и 1.

Как показано на приведенном выше графике, мы выбрали пороговое значение как 0,5, если функция прогнозирования вернула значение 0,7, то мы бы классифицировали это наблюдение как Класс 1 (DOG). Если наш прогноз вернул значение 0,2, мы бы классифицировали наблюдение как класс 2 (CAT).

Функция стоимости

Мы узнали о функции стоимостиJ(θ) вЛинейная регрессияфункция стоимости представляет собой цель оптимизации, то есть мы создаем функцию стоимости и минимизируем ее, чтобы мы могли разработать точную модель с минимальной ошибкой.

Если мы попытаемся использовать функцию стоимости линейной регрессии в «Логистической регрессии», то она будет бесполезна, поскольку в конечном итоге она станетневыпуклаяфункция со многими локальными минимумами, в которых было бы оченьсложновминимизировать стоимостьи найти глобальный минимум.

Для логистической регрессии функция Cost определяется как:

Источник

Функция sgn(x)

Функция (другое обозначение: ), читается «сигнум» (от лат. signum — знак) — кусочно-постоянная функция, определённая следующим образом:

Функция не является элементарной.

Часто используется представление

При этом производная модуля в нуле, которая, строго говоря, не определена, доопределяется средним арифметическим соответствующих производных слева и справа.

Функция применяется в теории обработки сигналов, в математической статистике и других разделах математики, где требуется компактная запись для индикации знака числа.

Содержание

История

Функцию sgn(x) ввёл Леопольд Кронекер в 1878 г., сначала он обозначал её иначе: [x]. В 1884 г. Кронекеру понадобилось в одной статье использовать, наряду с sgn, функцию «целая часть», которая также обозначалась квадратными скобками. Во избежание путаницы Кронекер ввёл обозначение , которое (за вычетом точки перед аргументом) и закрепилось в науке.

Свойства функции

См. также

Источники

Полезное

Смотреть что такое «Функция sgn(x)» в других словарях:

Sgn — График функции y = sgn x sgn (сигнум, от лат.&# … Википедия

Функция Хевисайда — Единичная функция Хевисайда Функция Хевисайда (единичная ступенчатая функция, функция единичного скачка, включенная единица) кусочно постоянная функция, равная нулю для отрицательных значений аргумента и единице для пол … Википедия

Непрерывная функция — Эта статья о непрерывной числовой функции. О непрерывных отображениях в различных разделах математики см. непрерывное отображение. Непрерывная функция функция без «скачков», то есть такая, у которой малые изменения… … Википедия

Производная функция — Производная основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел… … Википедия

Единичная функция Хевисайда — Функция Хевисайда, единичная ступенчатая функция, ступенька положения специальная математическая функция, чьё значение равно нулю для отрицательных аргументов и единице для положительных аргументов … Википедия

Источник

Логистическая регрессия для чайников: подробное объяснение

Дата публикации Aug 14, 2019

Хотел бы начать это путешествие ML с этим сообщением:

«Постарайтесь сначала понять формулировку проблемы, оставив в стороне свой тренированный интеллект, и попытайтесь проанализировать данные, как будто вы ничего о них не знаете. Ваше честное признание того, что вы ничего не знаете, приведет вас к процессу создания модели, достойной развертывания. «

Процесс важнее, чем результат в области науки о данных

В нашей последней статье о контролируемом ML мы рассмотрели модель линейной регрессии, которая имела дело с непрерывными атрибутами, чтобы определить влияние независимой переменной на зависимую переменную. Я бы пригласил вас пройти через это, чтобы получить правильный контекст.

Машинное обучение под наблюдением с использованием линейной регрессии: Часть 1

Понимание модели линейной регрессии

towardsdatascience.com

Все упражнение в модели линейной регрессии состояло в том, чтобы найти наилучшую линию соответствия, которая может предсказать влияние независимой переменной на зависимую или целевую переменную. Линейная регрессия имеет дело с проблемой, где нам нужно предсказать

Здесь мы пытаемся предсказать влияние / изменения, наблюдаемые на целевые переменные продажи / производительность, исходя из рабочего времени / возраста. Как насчет проблемы, когда мы хотим четко предсказать на основе входных данных, вероятность того, что пациенты будут диабетиками или не диабетиками, или предсказать вероятность того, что собака будет лаять в середине ночи или нет.

Проблема такого типа, когда нам нужно найти вероятность того, что событие произойдет или нет, или же оно будет истинным / ложным, называется проблемой классификации. Чтобы решить эту проблему, мы часто используем один из самых популярныхмодель ML под наблюдениемназывается,Модель логистической регрессии.

С этой информацией давайте начнем сегодняшнюю сессию по логистической регрессии, где мы рассмотрим

Что такое логистическая регрессия?

Логистическая регрессияэто статистический метод для анализа набора данных, в котором есть одна или несколько независимых переменных, которые определяют результат. Результат измеряется с помощью дихотомической переменной (в которой есть только два возможных результата). Он используется для прогнозирования двоичного результата (1/0, Да / Нет, Истина / Ложь) с учетом набора независимых переменных.

Вы также можете рассматривать логистическую регрессию как особый случай линейной регрессии, когда исходная переменная является категориальной, где мы используем логарифм шансов в качестве зависимой переменной. Проще говоря, он предсказывает вероятность возникновения события путем подгонки данных клогитфункция.

Помните, что в некоторых случаях зависимые переменные могут иметь более двух результатов, например, в браке / не замужем / в разводе, такие сценарии классифицируются какполиномиальная логистическая регрессия.Хотя они работают одинаково, чтобы предсказать результат.

Несколько знакомых примеров логистической регрессии:

Некоторые выдающиеся примеры, такие как:

Как работает логистическая регрессия?

Логистическая модель: сигмовидная функция

Давайте попробуем понять логистическую регрессию, понимая логистическую модель. Как и в случае линейной регрессии, давайте представим нашу гипотезу (Предсказание зависимой переменной) в классификации. В классификации наше представление гипотезы, которое пытается предсказать двоичный результат или o или 1, будет выглядеть так:

hθ (x) = g (θ T x) = 1/1 + e − θ T x,

Здесь g (z) = 1 / (1 + e ^ −z) называется lОгистическая функция или сигмовидная функция:

(г): представление логистической функции, которую мы также называем сигмовидной функцией. Из приведенного выше визуального представления сигмовидной функции мы можем легко понять, как эта кривая описывает многие реальные ситуации, такие как рост населения. На начальных этапах это показывает экспоненциальный рост, но через некоторое время, из-за конкуренции за определенные ресурсы (горлышко бутылки), скорость роста снижается, пока не достигнет тупиковой ситуации, и рост не будет

Вопрос здесь в том, как этологит(сигмоидальная функция) помогает нам определить вероятность классификации данных по различным классам. Давайте попробуем понять, как рассчитывается наша функция logit, что даст нам некоторую ясность

Математика за логистической функцией:

Шаг 1: Классификация входных данных должна быть в классе ноль или единица.

Во-первых, нам нужно вычислить вероятность того, что наблюдение принадлежит классу 1 (мы также можем назвать его положительным классом), используя функцию логистического отклика. В этом случае наш параметр z, как видно из приведенной ниже функции logit.

Log Odds (функция Logit):

Вышеприведенное объяснение также может быть понято с точки зрения логарифмических коэффициентов, что является своего рода пониманием вероятности классификации элементов на классы (1 или 0) с помощьюСТАВКИ:

Эти шансы, которые напоминают сходство с линейной регрессией, называютсялогит.

logit (P) = a + bX,

Шаг 2: Определение граничных значений для шансов

Теперь мы определим границу порога, чтобы четко классифицировать каждое заданное входное значение в один из классов.

Мы можем выбрать пороговое значение в соответствии с бизнес-проблемой, которую мы пытаемся решить, как правило, которая находится в районе 0,5 Таким образом, если ваши значения вероятности окажутся> 0,5, мы можем классифицировать такое наблюдение в тип класса 1, а остальные в класс 0.Выбор порогового значения обычно основывается на типах ошибок, которые бывают двух типов:ложные срабатывания и ложные отрицания.

Ложно-положительная ошибка возникает, когда модель прогнозирует класс 1, но наблюдение фактически принадлежит классу 0. Ложно-отрицательная ошибка допускается, когда модель прогнозирует класс 0, но наблюдение фактически принадлежит классу 1. Идеальная модель будет классифицировать все правильно классифицирует: все 1 (или истины) как 1, и все 0 (или ложь) как 0. Таким образом, мы имели бы FN = FP = 0.

Влияние пороговых значений:

1.Более высокое пороговое значение

Предположим, если P (y = 1)> 0,7. Модель является более строгой при классификации как 1, и, следовательно, будет сделано больше ошибок ложного отрицания.

2. Нижнее пороговое значение:

Предположим, если P (y = 1)> 0,3.

Модель теперь менее строгая, и мы классифицируем больше примеров как класс 1, поэтому мы делаем больше ошибок ложных срабатываний.

Путаница Матрица: путь к Choose Эффективное пороговое значение:

Матрица путаницы, также известная как матрица ошибок, является предиктором производительности модели для задачи классификации. Количество правильных и неправильных прогнозов суммируется со значениями количества и разбивается по каждому классу. Это лежит в основе путаницы.

Матрица путаницы показывает, каким образом ваша модель классификации находится в замешательстве, когда она делает прогнозы для наблюдений, она помогает нам измерить тип ошибки, которую делает наша модель, при классификации наблюдения по различным классам.

Ключевые части матрицы путаницы:

Ключевые показатели обучения из матрицы путаницы:

Матрица путаницы помогает нам изучать следующие метрики, помогая нам измерять производительность логистической модели.

Точность:

В целом, как часто верен классификатор?

Точность = (TP + TN) / общее количество засекреченных предметов = (TP + TN) / (TP + TN + FP + FN)

Точность:

Когда это предсказывает да, как часто это правильно?

Точность обычно используется, когда целью являетсяограничить количество ложных срабатываний(ФП). Например, с помощью алгоритма фильтрации спама, где наша цель состоит в том, чтобы свести к минимуму количество реальных электронных писем, которые классифицируются как спам

Точность = TP / (TP + FP)

Отзыв:

Когда это на самом деле положительный результат, как часто он предсказывает правильно?

Напомним = TP / (TP + FN), также известный как чувствительность.

f1-счет:

Это просто гармоническое среднее точности и напоминания:

f1-оценка = 2 * ((точность * отзыв) / (точность + отзыв))

Поэтому, когда вам нужно принять во внимание как точность, так и вспомнить, этот показатель f1 является полезным показателем для измерения. Если вы попытаетесь оптимизировать только отзыв, ваш алгоритм будет предсказывать, что большинство примеров будет принадлежать положительному классу, но это приведет к множеству ложных срабатываний и, следовательно, к низкой точности. Кроме того, если вы попытаетесь оптимизировать точность, ваша модель будет предсказывать очень мало примеров как положительные результаты (те, которые имеют наибольшую вероятность), но отзыв будет очень низким. Так что может быть полезно сбалансировать и рассмотреть оба варианта и увидеть результат.

Площадь AUC под кривой:

Специфичность или истинный отрицательный показатель= TN / (TN + FP)

Чувствительность или истинно положительный показатель= TP / (TP + FN)

ТакFPR, ложноположительный показатель = 1 – специфичность

Интуиция за кривой ROC:

Эта модель, которая предсказывает случайно, будет иметь ROC-кривую, которая выглядит как диагональная зеленая линия (как показано выше на рисунке). Это не дискриминационная модель. Чем дальше кривая от диагональной линии, тем лучше модель различает положительные и отрицательные значения в целом.

Типы логистической регрессии:

Поскольку мы поняли некоторые важные оговорки, связанные с логистической регрессией, пришло время взять некоторое практическое понимание на простом примере:

Реализация логистической регрессии:

Мы собираемся охватить это упражнение по созданию модели в следующие шаги:

Основная цель: прогнозировать диабет с использованием классификатора логистической регрессии.

1. Загрузка данных:

Мы будем использоватьНабор данных индийского диабета Pima, полученный из kaggle, Пожалуйста, загрузите данные из следующихссылка:

Напишите / скопируйте приведенный ниже код и запустите его в своем блокноте Juypter (убедитесь, что вы установилианаконда дистрибуцияв вашей системе), когда вы запустите этот фрагмент кода, вы увидите вывод, как показано на рис. 1.0

Исследовательский анализ данных:

Давайте изучим данный набор данных, чтобы найти

Анализ нечисловых и нулевых значений:

Напишите следующий фрагмент кода и скомпилируйте его:

Выход:

Вы обнаружите, что нет нечисловых атрибутов, так как возвращаемый массив имеет пустые значения индекса для каждого столбца.

Описательный анализ:

Давайте проведем некоторый описательный анализ, чтобы найти

Мы можем проанализировать каждый столбец с помощью пандописывают ()метод, чтобы получить статистическую сводку всех атрибутов. Этот анализ помогает нам определить, какой столбец сильно искажен, как выглядят хвосты, каковы средние, срединные и квартильные значения каждого столбца.

Запишите / скопируйте следующий код в свой блокнот и скомпилируйте его:

Быстрое наблюдение:

Давайте разберемся подробнее со всеми атрибутами dataframe, используя визуализацию парных участков.

Анализ парных участков.

Давайте посмотрим на целевой столбец ‘учебный классЧтобы понять, как данные распределяются между различными значениями.

Ключевые идеи:

Логистическая модель с использованием SkLearn & Python:

Импортные пакеты Sklearn:

ИмпортироватьЛогистическая регрессиямодель и другие необходимые пакеты, отsklearnпакет Python, как показано ниже:

Разделить данные на данные обучения и испытаний:

Давайте построим нашу модель:

Давайте посмотрим, как наша модель маркирует данные X_train, чтобы сделать классификацию:

Вы можете видеть, что с помощью функции model.predict (X_test) наша модель классифицировала каждый атрибут столбца (X-train) как 0/1 как прогноз

Время, чтобы измерить, как модель выступила (забил)

Перед этим давайте выясним значения коэффициентов плоскости (поверхности), которую наша модель нашла в качестве поверхности наилучшего соответствия, используя приведенный ниже код:

Который, получить в нашей функции сигмовидной

сигмоид, g (z) = 1 / (1 + e ^ −z).

Оценка модели:

Давайте посмотрим, как наша модель наилучшего соответствия сравнивается с нетренированными тестовыми данными, используя основную логистическую функцию (сигмовидная функция) мы обсуждали выше.

Показатель модели составляет 0,774, что в пересчете на процент составляет 77,4%. Это не на высоте. Кроме того, здесь необходимо указать, что ранее мы обсуждали, как диабетический класс был недостаточно представлен по сравнению с недиабетическим классом с точки зрения выборочных данных, поэтому мы должны редко полагаться на эту модель и проводить дальнейшие измерения с использованием метрик уровня класса матриц смешения. (Напомним, точность и т. Д.)

Давайте измерим производительность модели с помощью Confusion Metrics:

Наблюдение:

Давайте вычислим значение отзыва: показатель уровня класса для измерения производительности модели:

Отзыв:

Отзыв(Для недиабетических) = TP / (TP + FN)

Напомним = 132 / (132 + 14) = 132/146 = 0,90 = 90%

Отзыв(Для диабетиков) = TP / (TP + FN)

Напомним (для диабетиков) = 47/85 = 0,55 = 55%,

Эта модель работает плохо в случае диабетика, что вполне заметно из-за отсутствия доступных образцов данных для диабетического класса для моделирования, как мы обсуждали ранее.

Точность:

что является низким, особенно учитывая природу проблемы (здесь отрасль здравоохранения), которую мы пытаемся решить, где ожидается точность более 95%.

Что дальше?

Закрытие:

Хотелось бы закончить эту часть «Логистической регрессией» пищей для размышлений

Никогда не доверяйте тому, что вы знаете, вместо того, чтобы задавать вопросы и найти ответ для себя.

Источник