что показывает план матрица эксперимента
Полный факторный эксперимент
Полным факторным экспериментом (ПФЭ) называют такой эксперимент, при реализации которого определяется значение параметров оптимизации при всех возможных сочетаниях уровней варьирования факторов.
Планирование, проведение и обработка результатов ПФЭ состоит из следующих обязательных этапов:
· выбор области факторного пространства,
· составление план – матрицы эксперимента,
· реализация плана эксперимента,
· проверка воспроизводимости опытов,
· расчет значений коэффициентов регрессии,
· оценка значимости коэффициентов регрессии.
· проверка адекватности модели,
Выбор области факторного пространства
Выбор экспериментальной области факторного пространства связан, в первую очередь, с наличием предварительной информации. При выборе области эксперимента необходимо учитывать следующее.
1. Границы области определения факторов определяются с учетом таких ограничений:
1.1) принципиальные, которые не нарушаются ни при каких обстоятельствах (абсолютный ноль и т.п.);
1.2) технико-экономические (стоимость сырья, длительность процесса и т.п.);
1.3) налагаемые имеющимися аппаратными возможностями проведения эксперимента.
Выбор основного (нулевого) уровня
Наилучшим условиям протекания процесса, исходя из анализа априорной информации, является некоторая комбинация уровней факторов. Ее можно рассматривать как исходную точку для построения плана эксперимента. Назовем эту точку основным уровнем. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня. Выбор нулевого уровня – интуитивный выбор. Здесь нет никаких четких рекомендаций. Можно лишь, учитывая опыт планирования эксперимента, ориентироваться при выборе нулевого уровня на следующие обстоятельства.
1. Имеются сведения об одной оптимальной точке и нет информации о границах области определения факторов. В этом случае известную точку можно рассматривать как точку нулевого уровня.
2. Известны координаты наилучшей точки, но они или принадлежат, или близки к границам области определения факторов. В этом случае нулевой уровень следует выбирать со сдвигом от наилучших условий внутрь области определения параметра оптимизации.
3. Координаты точки неизвестны, но известны границы области определения факторов, в которых процесс протекает хорошо. Нулевой уровень следует выбирать как центральную точку известной области.
4. Известны координаты нескольких точек, в которых процесс идет хорошо. Если нет никаких дополнительных ограничений – выбор нулевого уровня случаен.
При решении интерполяционных задач приоритет при построении плана эксперимента следует отдавать не нулевому уровню, а установлению границ области определения факторов. После этого выбора нулевой уровень определяется автоматически.
Выбор интервалов варьирования факторами
При планировании цель экспериментатора состоит в том, чтобы для каждого уровня выбрать два (или несколько) уровня, на которых он будет варьироваться в эксперименте. В полном факторном эксперименте факторы варьируются на двух: нижнем и верхнем уровнях.
Представим координатную ось, на которой откладываются значения факторов, например, температуры изотермической выдержки бетона.
нижний уровень 80 верхний уровень
Если нулевой уровень имеет значение 80 С, тогда два других уровня указываются точками, симметричными относительно 80 С. В данном случае понятия «нижний» и «верхний» условны и могут быть не связаны с абсолютными значениями факторов, а для качественных факторов эти понятия вообще являются отвлеченными понятиями.
Интервалом варьирования называется некоторое числовое значение (для каждого уровня свое), прибавление которого к нулевому уровню дает значение верхнего уровня, вычитание из нулевого дает значение нижнего уровня.
Таким образом, задача выбора уровней сводится к простой задаче выбора интервалов варьирования факторами.
Кодирование факторов
Для упрощения записей и формализации расчетов приняты следующие обозначения уровней факторов в так называемых кодированных значениях:
· нижний уровень – [–1] или просто [–],
· нулевой уровень – [0],
· верхний уровень – [+1] или [+].
Для количественных факторов с непрерывной областью определения преобразование натуральных значений факторов в кодированные значения следует осуществлять, используя выражение

где Xi–кодированное значение фактора; Xi н –натуральное значение фактора; Xio н –натуральное значение основного уровня фактора; Ji –натуральное значение интервала варьирования фактора; i–номер фактора
Для качественных факторов, имеющих два уровня, один обозначается [–1], другой [+1]. Порядок значения не имеет.
Задача № 13. Пусть в задаче оптимизации процесса тепловой обработки бетона факторами выбраны: X1 – температура изотермической выдержки, С, X2 – длительность периода изотермической выдержки, час. Основной уровень и интервалы варьирования приведены в табл. 3
| Уровни | X1 н | X2 н |
| Основной уровень | ||
| Интервал варьирования |
Условия одного из опытов в кодированных выражениях выглядят следующим образом: X1= –0,5, X2=0,5. Определить правильные натуральные значения факторов данного опыта.
На выбор интервалов варьирования факторами накладываются ограничения снизу и сверху. Интервал варьирования не может быть меньше той ошибки, с которой фиксируется уровень фактора. В противном случае нижний и верхний уровни будут статистически неразличимы.
2.11. Составление план – матрицы эксперимента
| № | X1 | X2 | Y | Буквенное обозначение |
| -1 | -1 | Y1 | ||
| +1 | -1 | Y2 | a | |
| -1 | +1 | Y3 | b | |
| +1 | +1 | Y4 | ab |
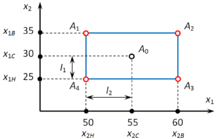
Графически точки матрицы планирования изображены на рис.5.
Площадь, ограниченная квадратом называется, областью эксперимента.
В задачах интерполяции область эксперимента есть область предсказываемых значений параметра оптимизации.
Существует иная форма записи матрицы планирования: порядковый номер фактора ставится в соответствии строчной букве латинского алфавита: X1 – a, X2 – b, X3 – c и т.д. Если для строки матрицы выписать буквы только для тех факторов, которые находятся на верхних уровнях, то условия опытов при этом задаются однозначно. Опыт со всеми факторами на нижних уровнях обозначается как [+1] (табл.5).
Для двух факторов все возможные комбинации факторов легко находятся простым перебором. С ростом числа факторов построение матрицы усложняется.
Существуют простые приемы построения матриц ПФЭ.
1. При добавлении нового фактора каждая комбинация уровней исходного плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Поэтому следует записать исходный план для одного уровня нового фактора, а затем повторить его для другого уровня.
| № | X1 | X2 | X3 |
| –1 | –1 | –1 | |
| +1 | –1 | –1 | |
| –1 | +1 | –1 | |
| +1 | +1 | –1 | |
| –1 | –1 | +1 | |
| +1 | –1 | +1 | |
| –1 | +1 | +1 | |
| +1 | +1 | +1 |
2. Второй прием основан на чередовании знаков. В первом столбце знаки меняются поочередно, во втором – через два, в третьем – через четыре, в четвертом – через восемь и т.п.
В общем случае для линейных моделей ПФЭ типа 2 2 геометрический образ модели представляет гиперплоскость в (K+1)-мерном факторном пространстве, что исключает возможность зрительного восприятия образа, кроме случая, когда К=2 (рис. 4).
Рассмотрим некоторые свойства матриц, определяющие качество моделей.
Эксперимент планируется для того, чтобы получить математическую модель, обладающую некоторыми оптимальными свойствами: оценки коэффициентов модели должны быть наилучшими; точность предсказаний параметра оптимизации не должна зависеть от направления в факторном пространстве. Итак, что же это за свойства?
Сначала рассмотрим свойства отдельных столбцов матрицы.
1. Симметричность относительно центра эксперимента: алгебраическая сумма элементов вектора-столбца каждого фактора равна нулю
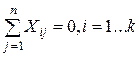
2. Условие нормировки: сумма квадратов элементов каждого столбца равна числу опытов
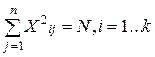
Теперь рассмотрим свойства совокупности столбцов.
3. Ортогональность матрицы планирования: сумма почленных произведений любых двух вектор – столбцов матрицы равна нулю.

4. Ротатабельность матрицы: точки в матрице планирования подбираются таким образом, чтобы точность предсказаний значений параметра оптимизации была бы одинакова на равных расстояниях от центра эксперимента в независимости от направления рассмотрения.
Рандомизация опытов
На изучаемый процесс кроме варьируемых факторов оказывают влияние и другие, зачастую неизвестные исследователю. Для того, чтобы внести элемент случайности влияния этих факторов на результаты опыта, устанавливается случайный порядок постановки опытов во времени. Эта процедура и называется рандомизацией. Для ее осуществление можно использовать таблицы случайных чисел, лотерею и т.п.
Реализация эксперимента
Реализация плана предполагает проведение опытов в соответствии с условиями план – матрицы при обеспечении заданных систем ограничений эксперимента во времени и пространств.
Разберем дальнейшие расчеты на конкретном примере.
Упражнение № 5 Построить на данных табл. 6 математическую модель процесса влияния добавок CaCl2 (X1) и С – 3 (X2) на прочность равноподвижных бетонных смесей через 28 суток нормального твердения.
2.14. Проверка воспроизводимости опытов план – матрицы
При одинаковом числе параллельных результатов опыта на каждом сочетании уровней факторов воспроизводимость процесса проверяется по расчетному значению критерия Кохрена, при несовпадении – по критерию Фишера.
Процесс считается воспроизводимым, если соответствующие расчетные значения критериев не превышают табличных значений. Если это не выполняется, необходимо принять меры к уточнению измерений в опыте с максимальной дисперсией.
В рассматриваемом нами примере построчные дисперсии приведены в табл. 6.
Критерий Кохрена Gрасч=16/30=0,533. Табличное значение критерия Кохрена (прил. Г) G(0.05,2,4)=0,7679. Так как выполняется неравенство Gрасч 2 <y> (ошибкой опыта).
Величина дисперсии воспроизводимости в рассматриваемом примере S 2 <y>=30/4=7,5.
В случае воспроизводимого процесса рассчитываются коэффициенты регрессии.
Полный факторный эксперимент
Полный факторный эксперимент (ПФЭ) – совокупность нескольких измерений, удовлетворяющих следующим условиям:
Преимуществами полного факторного эксперимента являются
Содержание
Предварительные сведения
Оценка параметров системы
В практической деятельности часто требуется оценить параметры некоторой системы, то есть построить её математическую модель и найти численные значения параметров этой модели. В качестве исходных данных для построения модели служат результаты эксперимента, который представляет собой совокупность нескольких измерений, выполненных по определённому плану. В простейшем случае план является описанием условий проведения измерений, то есть значения входных параметров (факторов) во время измерения.
В качестве примера систем, оценка параметров которых актуальна с практической точки зрения, могут служить различные технологические процессы. Для иллюстрации рассмотрим процесс фотолитографии.
Фотолитография представляет собой нанесение рисунка на поверхность фотографическим методом. Она состоит из следующих этапов: подготовка поверхности, нанесение фоточувствительной эмульсии (фоторезиста), сушка, установка трафарета или пластины с негативным рисунком, экспозиция (засвечивание) ультрафиолетовыми лучами, травление (проявление). Поскольку технологические тонкости фотолитографии в данном контексте не важны, в качестве основных факторов, влияющих на процесс литографии, будем считать толщину фоточувствительной эмульсии d(в микронах) и время экспозиции t(в секундах). Выходным параметром (откликом) процесса будем считать его разрешение R, то есть максимальное количество различимых линий, которые возможно провести на одном миллиметре поверхности. Эта величина определяется путём нанесения на поверхность специального тестового изображения.
Итак, технологический процесс фотолитографии описывается некоторой функцией вида
Построение модели технологического процесса позволяет выявить поведение отклика системы в зависимости от изменения факторов и тем самый найти пути для оптимизации технологии. Для данного конкретного случая — выбрать такую толщину эмульсии и время экспозиции, которые обеспечат наилучшее качество изображения.
В общем случае отклик системы описывается некоторой функцией 
Математическая модель системы получается в результате апроксимации этой функции какой-либо другой функцией, например линейной

где 
На рисунке в графическом виде представлен процесс построения линейной модели процесса фотолитографии, где 






Зная коэффициенты модели 


Матрица эксперимента
Предположим, исходные параметры технологического процесса составляют: толщина плёнки 55 мкм, время экспозиции – 30 с, то есть
Возьмём верхние и нижние значения обоих факторов так, чтобы они располагались симметрично относительно текущего значения, например

Составим таблицу, в которой значения обоих факторов находятся во всех возможных сочетаниях и проведём измерения в этих точках (значения отклика даны условно):
Полагая, что линейная модель процесса имеет вид

на основании полученных результатов можно составить систему четырёх уравнений с двумя переменными. Ниже показана эта система, а также её сокращённая запись в виде матрицы. Матрицу данного вида назовём матрицей эксперимента.
В матрице эксперимента второй и третий столбцы представляют собой значения факторов, четвёртый столбец – значения отклика системы, а первый столбец содержит единицы, соответствующие единичным коэффициентам свободного члена модели 

Решение системы
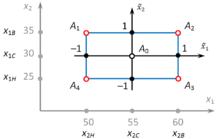
Чтобы облегчить решение системы, проведём нормировку факторов. Верхним значениям факторов присвоим нормированное значение +1, нижним значениям – нормированное значение –1, среднему значению – нормированное значение 0. В общем виде нормировка фактора выражается формулой
С учётом нормировки факторов система уравнений и матрица эксперимента примут следующий вид:
Поскольку сумма членов во втором и третьем столбце матрицы равны нулю, свободный член модели можно найти, сложив все четыре уравнения:

Чтобы найти какой-либо другой коэффициент модели, нужно изменить знаки в уравнениях таким образом, чтобы в соответствующем столбце оказались одни единицы, после чего сложить все четыре уравнения:



Таким образом, линейная модель технологического процесса в окрестностях точки (55, 30) имеет вид
В общем случае решение системы будет выглядеть как
Возврат к ненормированным факторам
Переход от нормированных к ненормированным факторам осуществляется обратным преобразованием
Чтобы найти параметры модели для ненормированных координат, подставим выражения для нормированных координат в уравнение модели:



Cравнивая последнее выражение с выражением для линейной модели в ненормированных координатах

получим выражения для параметров модели:


Для приведённого выше примера


Окончательно получаем модель в естественных координатах:

Полный факторный эксперимент
Матрица ПФЭ в общем виде
В общем виде матрица полного факторного эксперимента с n факторами имеет вид
Свойства матрицы ПФЭ
Матрица ПФЭ обладает следующими свойствами:
где 

Вычисление коэффициентов линейной модели
Коэффициенты линейной модели в нормированных координатах вычисляются по формулам:
Коэффициенты линейной модели в естественных (ненормированных) координатах вычисляются по формулам: