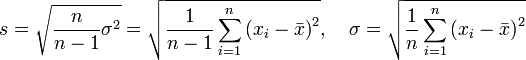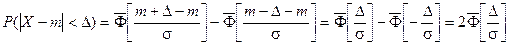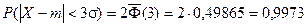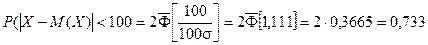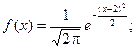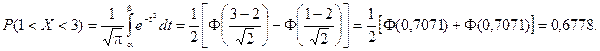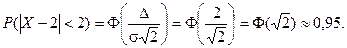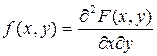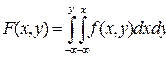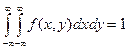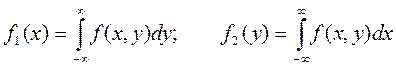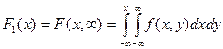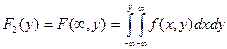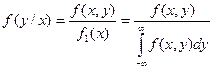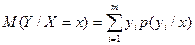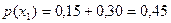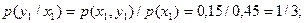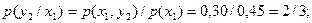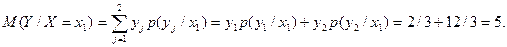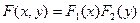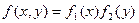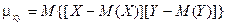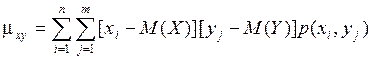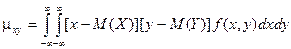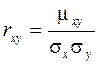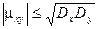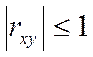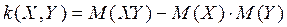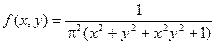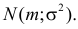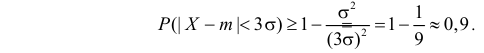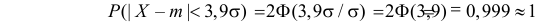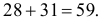что показывает правило трех сигм
Правило трёх сигм
Стандартное отклонение (иногда среднеквадратичное отклонение) — в теории вероятности и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно её математического ожидания. Измеряется в единицах измерения самой случайной величины. Равен корню квадратному из дисперсии случайной величины. Стандартное отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
где 
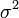
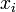
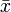
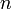
Следует отметить отличие стандарта (в знаменателе n − 1 ) от корня из дисперсии(среднеквадратического отклонения)(в знаменателе n ), при малом объёме выборки оценка дисперсии через последнюю величину является несколько смещенной, при бесконечно большом объёме выборки разница между указанными величинами исчезает. Выборка — лишь часть генеральной совокупности. Генеральная совокупность — абсолютно все возможные результаты. Получить результат, не входящий в генеральную совокупность абсолютно невозможно в принципе. Для случая с бросанием монетки генеральной совокупностью является : решка, ребро, орел. а вот пара орел-решка уже лишь выборка. Для генеральной совокупности математическое ожидание совпадает с истинным значением оцениваемого параметра. А вот для выборки не факт. Математическое ожидание выборки имеет смещение относительно истинного значения параметра. В силу этого, среднеквадратичная ошибка больше чем дисперсия, так как дисперсия — математическое ожидание квадрата отклонения от среднего значения, а среднеквадратичное отклонение — математическое ожидание отклонения от истинного значения. Разница в том, от чего ищем отклонение, когда дисперсия, то от среднего и не важно истинное это среднее или ошибочно, а когда среднеквадратичное отклонение, то ищем отклонение от истинного значения.
Полезное
Смотреть что такое «Правило трёх сигм» в других словарях:
Шесть сигм — (англ. six sigma) концепция управления производством, разработанная в корпорации Motorola в 1980 е годы и популяризированная в середине 1990 х после того, как Джек Уэлч применил её как ключевую стратегию в General Electric. Суть… … Википедия
Среднеквадратическое отклонение — (синонимы: среднеквадратичное отклонение, квадратичное отклонение; близкие термины: стандартное отклонение, стандартный разброс) в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины … Википедия
Выборочное стандартное отклонение — Стандартное отклонение (иногда среднеквадратичное отклонение) в теории вероятности и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно её математического ожидания. Измеряется в единицах… … Википедия
Нормальное распределение — Плотность вероятности Зеленая лин … Википедия
Отряд Кремнероговые губки (Cornacuspongida) — Самая многочисленная группа губок. Это преимущественно мягкие эластичные формы. Скелет их образован одноосными иглами. Всегда имеется в том или ином количестве спонгин, с помощью которого иглы склеиваются между собой в пучки или волокна … Биологическая энциклопедия
Математи́ческие ме́тоды — в медицине совокупность методов количественного изучения и анализа состояния и (или) поведения объектов и систем, относящихся к медицине и здравоохранению. В биологии, медицине и здравоохранении в круг явлений, изучаемых с помощью М.м., входят… … Медицинская энциклопедия
Расчет себестоимости по видам деятельности — Содержание 1 Менеджмент на основе хозяйственной деятельности 2 Разработка деловой ситуации 3 … Википедия
Расчёт себестоимости по видам деятельности — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Расчёт себестоимости по видам деятельности (Activity Based Costing, ABC) это специальная модель описания затрат, которая идентифицирует работы фирмы … Википедия
Правило трёх сигм



При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т.
Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.
Получаем:
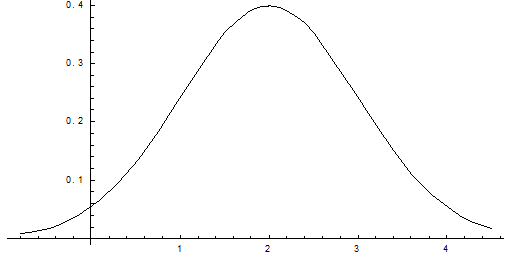
Плотность распределения имеет вид:
Построим график:
Найдем вероятность попадания случайной величины в интервал (1; 3).
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2.
Тот же результат может быть получен с использованием нормированной функции Лапласа.
Центральная предельная теорема Ляпунова
На практике для большинства случайных величин выполняются условия теоремы Ляпунова.
Если известна плотность распределения, то функция распределения может быть легко найдена по формуле:
Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности равен единице.
По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины.
Условные законы распределения
Как было показано выше, зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему.
Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения.
В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами.
Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими.
Все это приводит к необходимости рассмотрения условных законов распределения.
Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.
Условная плотность распределения вычисляется по формулам:
Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.
Условное математическое ожидание
Для непрерывных случайных величин:
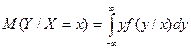
где f(y/x) – условная плотность случайной величины Y при X=x.
Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y.
X = x1 = 1 для дискретной двумерной случайной величины, заданной таблицей:
| Y | X | |||
| x1=1 | x2=3 | x3=4 | x4=8 | |
| y1=3 | 0,15 | 0,06 | 0,25 | 0,04 |
| y2=6 | 0,30 | 0,10 | 0,03 | 0,07 |
Аналогично определяются условная дисперсия и условные моменты системы случайных величин
Зависимые и независимые случайные величины
Случайные величины называются независимыми, если закон распределения одной из них не зависит от того какое значение принимает другая случайная величина.
Понятие зависимости случайных величин является очень важным в теории вероятностей.
Условные распределения независимых случайных величин равны их безусловным распределениям.
Определим необходимые и достаточные условия независимости случайных величин.
Аналогичную теорему можно сформулировать и для плотности распределения:
Практически используются формулы:
Для дискретных случайных величин:
Для непрерывных случайных величин:
Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.
Корреляционный момент имеет размерность, равную произведению размерностей случайных величин Х и Y. Этот факт является недостатком этой числовой характеристики, т.к. при различных единицах измерения получаются различные корреляционные моменты, что затрудняет сравнение корреляционных моментов различных случайных величин.
Для того, чтобы устранить этот недостаток применятся другая характеристика – коэффициент корреляции.
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.
Свойство : Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий.
Свойство : Абсолютная величина коэффициента корреляции не превышает единицы.
Случайные величины называются коррелированными, если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю.
Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод о их независимости.
Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.
Часто по заданной плотности распределения системы случайных величин можно определить зависимость или независимость этих величин.
Наряду с коэффициентом корреляции степень зависимости случайных величин можно охарактеризовать и другой величиной, которая называется коэффициентом ковариации. Коэффициент ковариации определяется формулой:
Выяснить являются ли независимыми случайные величины Х и Y.
Для решения этой задачи преобразуем плотность распределения:
Правило «трех сигм»:
Пусть случайная величина X имеет закон распределения
т.е. отклонения, большие 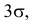
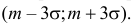
Поэтому правилом «трех сигм» иногда пользуются не печалясь о том, что случайная величина вовсе не имеет нормального закона распределения.
Замечание. Последние годы все чаще предпочитают брать не 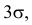
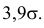
(Величина 0,999 впечатляет больше, нежели 0,997!)
Пример:
Монета подброшена 100 раз. Герб выпал 30 раз. Можно ли считать, что монета было симметричной?
Решение. Подбрасывание монеты можно считать независимым опытом, число которых 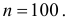
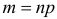
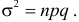
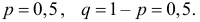
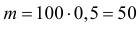
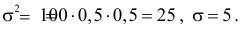
Ответ. При симметричной монете такой результат практически невозможен.
Пример:
Некто утверждает, что он экстрасенс. Для проверки был проделан следующий опыт. Взято пять карточек с рисунками простейших геометрических фигур. Испытатель выбирает карточку наугад, а испытуемый, находясь в соседней комнате, пытается определить, руководствуясь сверхчувственным восприятием, какая карточка выбрана экспериментатором. Карточки перемешиваются. Затем опыт повторяется. Так проделали 100 раз. Оказалось, что в 28 случаях испытуемый правильно назвал карточку. Есть ли основания считать, что имело место сверхчувственное восприятие?
Решение. Естественно предположить, что 28 совпадений произошли случайно. Вероятность угадать нужную карточку равна 1/5. Угадывание каждой карточки можно считать независимым опытом. Так как опытов много (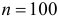
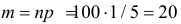
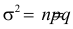
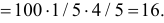
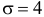
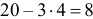
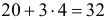
Замечание. Предположим, что экстрасенс все-таки настаивает на своем сверхчуственном восприятии. Серию опытов повторили. Совпадений оказалось 31. В этом случае всего опытов 
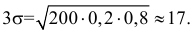
Такое число совпадений при простом угадывании практически невозможно. Это может послужить поводом для тщательной проверки условий эксперимента (подавляющее большинство так называемых экстрасенсов – откровенные жулики). Или следует настоять на лабораторном обследовании экстрасенса (от чего экстрасенсы всячески уклоняются, их стихия – работа на публику).
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Что показывает правило трех сигм
На основании этого правила для исключения из результатов измерений грубых ошибок (промахов, аномальных значений) часто используют критерий трёх сигм: значения нормально распределённой случайной величины, отклоняющиеся от математического ожидания М(х) больше, чем на три сигмы, маловероятны (вероятность равна 1 – 0.9973 = 0.0027), и потому являются грубыми ошибками. Т.е. значение xi – грубая ошибка, если
Критерий трёх сигм применяют обычно для быстрого приближённого определения грубых ошибок в выборке. Известны более обоснованные критерии аномальности при нормальном распределении, например критерии Смирнова (Граббса), Диксона, Ирвина и другие. Преимуществами критерия трёх сигм считается то, что он прост, нагляден и легко запоминается, при его применении не нужны таблицы.
Формализовать проверку на грубые ошибки по критерию трёх сигм с точки зрения статистической проверки гипотез можно так:
— нулевая гипотеза Н0: все значения выборки принадлежат одному и тому же нормальному распределению
— конкурирующая (альтернативная) гипотеза Н1: значения выборки, отстоящие от математического ожидания больше, чем на три сигмы, принадлежат другому распределению.
Таким образом, все значения, удовлетворяющие правилу (1), являются грубыми ошибками.
На практике параметры распределения чаще всего не известны с достаточной точностью, и используют их выборочные оценки – среднее значение xср и выборочное СКО (среднеквадратическое отклонение) s. При этом уровни значимости заметно отличаются от тех, когда параметры распределения известны.
Тогда выражение (1), т.е. условие для определения грубых ошибок, превращается в
Все значения выборки, удовлетворяющие условию (2), считаются грубыми ошибками.
Возможны также ситуации, когда математическое ожидание оценивают по хср, а СКО известно с высокой точностью – например, при оценке дисперсии (и, соответственно, СКО) по сериям измерений. Тогда выражение (1), т.е. условие для определения грубых ошибок, превращается в (3):
Все значения выборки, удовлетворяющие условию (3), считаются грубыми ошибками.
Расчёт хcр и s в (2) и (3) может проводиться по двум вариантам:
Второй вариант более сложен, что в значительной мере уменьшает преимущества критерия трёх сигм по сравнению с другими. В этой статье рассмотрен первый вариант, когда при оценке параметров распределения учитываются все значения выборки.
Приемлемые уровни значимости принимали в пределах 0,01…0,1, т.к. в статистических расчётах обычно принимают уровни значимости из этого диапазона. При этом величина k в (2) и (3) может отличаться от 3 в зависимости от объёма выборки n (в этом случае встречается также наименование «критерий Райта»).
Для уточнения величины k рассчитывали методом статистического компьютерного моделирования уровни значимости при различных k и n, при моделировании 1 млн. выборок из стандартного нормального распределения. При этом для доверительной верояности 0,9973 погрешность определения уровня значимости составляет ±0,0003 для уровня 0,01 и ±0,0009 для уровня 0,1 [1]. Значения k принимали относительно «круглыми», чтобы критерий оставался достаточно простым и сравнительно легко запоминаемым. Так находили диапазоны значений n, в которых при определённом k уровни значимости находятся в пределах 0,01…0,1. Крайние значения диапазонов n также принимали по возможности достаточно «круглыми». Некоторые из результатов моделирования показаны в табл. 2 и табл. 3. Если в этих таблицах указано, что вероятность равна нулю, то она, по крайней мере, меньше 0,0005.
В таблицах 2 и 3 приведены результаты до n=10000. При более высоких n, поскольку оценки параметров очень близки к парамерам, уровни значимости можно рассчитать так:
По данным таблиц 2 и 3 можно рекомендовать следующее: при неизвестной дисперсии определять промахи по (2) и значениях k:
k = 3, если n = 20. 55
k = 3,5, если n = 56. 250
k = 4, если n = 251. 1700
k = 4,5, если n = 1701. 10000
При известной дисперсии определять промахи по (3) и значениях k:
k = 3, если n = 8..40
k = 3,5, если n = 41..200
k = 4, если n = 201..1600
k = 4,5, если n = 1601..10000
        Далее     Содержание
© В.В.Заляжных
При использовании материалов ставьте прямую индексируемую ссылку