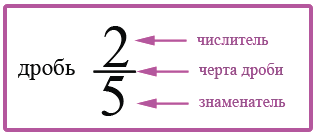что показывает знаменатель и числитель
Доли. Обыкновенные дроби
Нам известно, что при подсчете чего-либо мы используем натуральные числа, но часто приходится что-то целое делить на части. Например, нам дан апельсин:
Допустим, нам надо разделить апельсин на 6 равных частей:
В этом случае каждую часть называют долей. То есть целый апельсин разделили на 6 частей, поэтому мы можем сказать, что апельсин это 1 целая, и 6 долей апельсина тоже составляет 1 целую:
Название долей зависит от числа частей. Каждая доля в нашем случае будет называться «одной шестой долей апельсина» или, короче, «одной шестой апельсина«. Если апельсин поделить на 8 частей, то мы получим восьмые доли. При этом, чем на большее число частей делят целое, тем меньше доля.
Например, рассмотрим брусок:
Разделим его на 5 частей:
То есть мы получим пятые доли бруска. Закрасим две части красным:
Теперь закрасим три части бруска:
Мы закрасили три пятые доли. Дробь, обозначающая эти доли, записывается так: 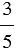
Теперь закрасим желтым цветом пять частей бруска:
Мы закрасили пять пятых долей, то есть мы закрасили весь брусок. Дробь, обозначающая эти доли, записывается так: 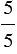
Рассмотрим рисунок ниже:
Определения
Правильная дробь – это дробь, числитель которой меньше знаменателя.
Неправильная дробь – это дробь, у которой числитель больше знаменателя или равен ему.
Поделись с друзьями в социальных сетях:
Числитель и знаменатель
Числитель дроби — это число, стоящее в записи обыкновенной дроби над дробной чертой, то есть сверху. Числитель показывает количество долей.
Знаменатель дроби — это число, стоящее в записи дроби под дробной чертой, то есть снизу. Знаменатель показывает, какие это доли и на сколько равных частей разделена единица.
Дробная черта — это горизонтальная черта в записи дроби, которая отделяет числитель и знаменатель друг от друга.
Вместе, числитель и знаменатель дроби, называются членами дроби.
Условились считать, что дробная черта означает деление верхнего числа на нижнее, поэтому:
Любую операцию деления можно записать в виде дроби. И наоборот, любую дробь можно записать в виде операции деления.
Как читать запись обыкновенных дробей
По этому правилу читаются все обыкновенные дроби.
Пример 1. Прочитайте дробь 
Пример 2. Прочитайте дробь 
Пример 3. Прочитайте дробь 
Обыкновенные дроби. Числитель, знаменатель. Доли в дробях.
Обыкновенные дроби. Понятие дроби. Доли в дробях.
Дроби мы постоянно используем в жизни. Например, когда едим торт с друзьями. Торт можно разделить на 8 равных частей или на 8 долей. Доля – это равная часть от чего-то целого. Четыре друга съели по кусочку торта. Четыре взяли из восьми кусочков можно записать математически в виде обыкновенной дроби \(\frac<4><8>\), читается дробь “четыре восьмых” или “четыре деленное на восемь”. Обыкновенную дробь еще называют простой дробью.
Дробная черта заменяет деление:
\(4 \div 8 = \frac<4><8>\)
Это мы записали доли в дробях. В буквенном виде будет так:
\(\bf m \div n = \frac
4 – числитель или делимое, находится вверху над дробной чертой и показывает сколько частей или долей из общего было взято.
8 – знаменатель или делитель, находится внизу под дробной чертой и показывает общее количество частей или долей.
Если мы приглядимся внимательно, то увидим, что друзья съели половину торта или одну часть из двух. Запишем в виде обыкновенной дроби \(\frac<1><2>\), читается “одна вторая”.
Рассмотрим еще пример:
Имеется квадрат. Квадрат разделили на 5 равных частей. Две части закрасили. Запишите дробь для закрашенных частей? Запишите дробь для не закрашенных частей?
Две части закрасили, а всего частей пять, поэтому дробь будет иметь вид \(\frac<2><5>\), читается дробь “две пятых”.
Три части не закрасили, всего частей пять, поэтому дробь запишем так \(\frac<3><5>\), читается дробь “три пятых”.
Разделим квадрат на более мелкие квадраты и запишем дроби, для закрашенных и не закрашенных частей.
Закрашенных 4 части, а всего 25 частей. Получаем дробь \(\frac<4><25>\), читается дробь “четыре двадцать пятых”.
Не закрашенных 21 частей, а всего 25 частей. Получаем дробь \(\frac<21><25>\), читается дробь “двадцать один двадцать пятых”.
Любое натуральное число можно представить в виде дроби. Например:
Любое число делиться на единицу, поэтому это число можно представить в виде дроби.
Вопросы по теме “обыкновенные дроби”:
Что такое доля?
Ответ: доля – это равная часть от чего-то целого.
Что показывает знаменатель?
Ответ: знаменатель показывает на сколько всего частей или долей поделено.
Что показывает числитель?
Ответ: числитель показывает сколько частей или долей было взято.
Дорога составляла 100м. Миша прошел 31м. Запишите дробью выражение сколько прошел Миша?
Ответ:\(\frac<31><100>\)
Что такое обыкновенная дробь?
Ответ: обыкновенная дробь – это отношение числителя к знаменателю, где числитель меньше знаменателя. Пример, обыкновенных дробей \(\frac<1><4>, \frac<3><7>, \frac<5><13>, \frac<9><11>…\)
Как перевести натуральное число в обыкновенную дробь?
Ответ: любое число можно записать в виде дроби, например, \(5 = \frac<5><1>\)
Задача №1:
Купили 2кг 700г дыни. Мише отрезали \(\frac<2><9>\) дыни. Чему равна масса отрезанного кусочка? Сколько граммов дыни осталось?
Решение:
Переведем килограммы в граммы.
2кг = 2000г
2000г + 700г = 2700г всего весит дыня.
Мише отрезали \(\frac<2><9>\) дыни. В знаменателе стоит число 9, значит на 9 частей разделили дыню.
2700 : 9 =300г масса одного кусочка.
В числители стоит число 2, значит надо Мише дать два кусочка.
300 + 300 = 600г или 300 ⋅ 2 = 600г столько дыни съел Миша.
Чтобы найти какая масса дыни осталась нужно вычесть от общей массы дыни съеденную массу.
2700 — 600 = 2100г осталось дыни.
Дроби
В жизни нам нередко приходится пользоваться не только целыми числами, но и их частями (долями).
Доли — это равные части целого.
Устройство обыкновенной дроби
Рассмотрим круг, разделённый на четыре равных части.
Сколько частей круга закрашено? Одна.
На сколько частей разделён целый круг? На четыре части.
Какая часть целого круга закрашена? Ответ:
| 1 |
| 4 |
Число, стоящее над дробной чертой, называется числителем. Числитель показывает, сколько долей взяли (закрасили) у целого.
Число, стоящее под дробной чертой, называется знаменателем. Знаменатель показывает, на сколько равных долей разделено целое.
Чтобы запомнить, что знаменатель — это нижняя часть дроби, выучите стихотворение:
Знамёна упали, знаменатель — внизу,
А числа сражались, числитель — вверху.
Иными словами, в круге закрашено
| 3 |
| 8 |
круга.
Некоторые обыкновенные дроби имеют особые названия. Знать, как называются такие дроби, надо наизусть.
Обыкновенные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо: