что понимается под приемом генерации пароля формула комбинация методов сдо
Как генерировать и запоминать сложные пароли, или Генератор мнемонических паролей
В последнее время это стало проблемой. Люди спрашивают Google по-всякому: «самый сложный пароль в мире», » помогите придумать пароль», » лучший генератор паролей», » криптостойкий пароль».
Каждый из вас может стать генератором сложных мнемонических паролей. Для этого предлагаю несколько советов, которые помогут вам генерировать и запоминать сложные пароли. Только я не хочу, чтобы люди становились хомячками и бездумно копировали мою систему. Не будьте хомячками, пожалуйста.
В течение многих лет я использовал такие пароли, как будто клал ключ от квартиры под коврик. Герои любимых видеоигр. Моя фамилия и две последние цифры моего года рождения. Слово «пароль» задом наперед.
Теперь у меня есть довольно простая система генерации и запоминания паролей: легкая, неприступная и уникальная. Можно ее назвать красивым выражением » генератор мнемонических паролей». Она делится на три части: случайный ключ, контекст и формулу.
Система «ключ + контекст + формула»
Пристально рассмотрим каждую часть, затем я приведу несколько примеров.
Не беспокойтесь слишком много о том, как бы не забыть этот ключ. Вы будете использовать его повсюду, и мышечная память начнет действовать в ближайшее время.
Красота этой системы заключается в том, что если кто-то взломает одну из ваших учетных записей и получит ваш пароль, у них будет только один уникальный пароль, который не нужен больше нигде. И если вам нужно поменять пароли (а это вы должны делать время от времени), вы можете изменить либо формулу, либо ключ. Это означает, что для восстановления старых забытых паролей нужна только формула или ключ.
Примеры легкой генерации сложных паролей
Давайте рассмотрим несколько примеров, чтобы вы могли лучше представить себе, о чем я говорю.
Пример 1: простая формула
Пример 2. сложная формула
Две заметки и важное предупреждение
2) в Gmail или Twitter вам может понадобиться несколько паролей для одного домена. В этом случае я бы добавил в формулу новый слой, основанный на создаваемой учетной записи (например, первые буквы почтового логина Gmail или имени пользователя Twitter).
Эту страницу находят по запросам:
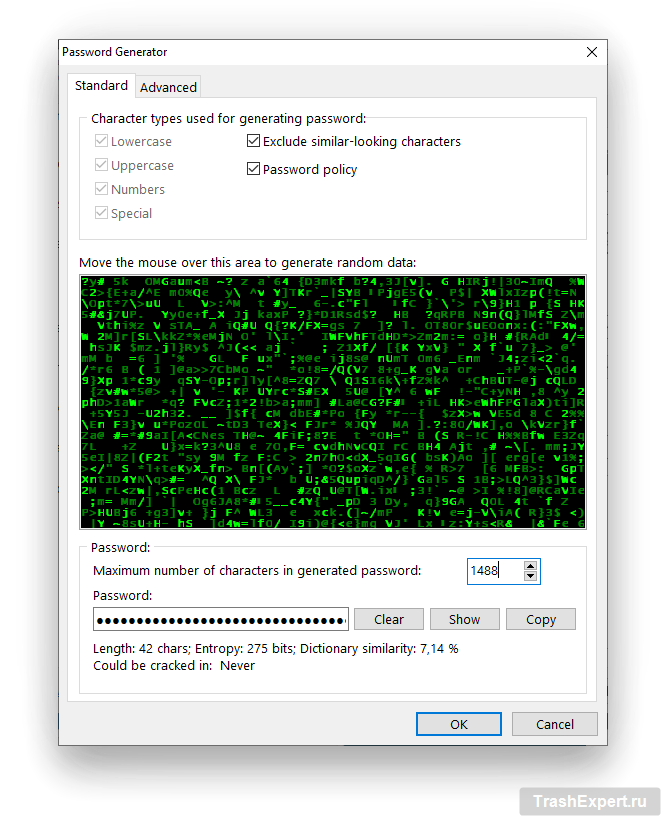
Как использовать генератор случайных паролей
Необходимо защищать ваши учётные записи на сайтах и в приложениях. Вам вряд ли понравится, что кто-то отправляет сообщения от вашего имени или тратит ваши деньги на покупки. Сейчас учётные записи защищаются при помощи паролей, хотя это далеко не лучший вариант.
Если вы используете очень простые пароли или используете один и тот же пароль везде, вас могут взломать. Но если вы сделаете пароль слишком сложным, то можете забыть его и не войти в свой аккаунт. Единственный способ использовать надёжный уникальный пароль для каждого сайта — это установить менеджер паролей. Тогда вы сможете на каждом сайте применять случайным образом выбранные уникальные сложные пароли.
Почти каждый менеджер паролей включает в себя генератор паролей, поэтому не придётся придумывать случайные пароли самостоятельно. Впрочем, при желании можно создать собственный генератор случайных паролей. Не все генераторы паролей одинаковы. Зная принципы их работы, можно выбрать наиболее подходящий и эффективно использовать его.
Генераторы паролей — случайные или нет?
Когда вы бросаете пару кубиков, вы получаете случайный результат. Никто не может предсказать, какое число у нас выпадет. Но в компьютерной сфере физические объекты, такие как игральные кости, отсутствуют. Существует несколько источников случайных чисел, основанных на радиоактивном распаде, но вы не найдёте их в среднестатистическом менеджере паролей.
Менеджеры паролей и другие компьютерные программы используют так называемый псевдослучайный алгоритм. Этот алгоритм начинается с числа, называемого начальным числом. Алгоритм обрабатывает начальное число и получает новое число без прослеживаемой связи со старым, и новое число становится следующим начальным числом. Исходное число никогда не появится снова, пока не появятся все остальные числа.
Если начальное число было 32-битным целым числом, это означает, что алгоритм будет обрабатывать 4 294 967 295 других чисел перед повторением.
Это нормально для повседневного использования и подходит для большинства генерирующих пароли людей. Однако теоретически опытный хакер может определить используемый псевдослучайный алгоритм. Зная его и начальное значение, хакер мог бы воспроизвести последовательность случайных чисел (хотя это сложно).
Такой вид направленного взлома чрезвычайно маловероятен, за исключением целенаправленной атаки со стороны государства или корпоративного шпионажа. Если вы подвергаетесь такой атаке, ваш антивирус вряд ли сможет вас защитить. К счастью, вы наверняка не станьте мишенью такого рода кибершпионажа.
Тем не менее, некоторые менеджеры паролей активно работают над устранением даже отдаленной возможности такой целенаправленной атаки. Включая ваши собственные движения мыши или случайные символы в случайный алгоритм, они получают действительно случайный результат. Среди тех, кто предлагает такую рандомизацию в реальном мире, — AceBIT Password Depot, KeePass и Steganos Password Manager.
На скриншоте выше показан рандомизатор в виде матрицы Password Depot; да, символы падают, когда вы двигаете мышью.
Менеджеры паролей уменьшают случайность
Конечно, генераторы паролей не возвращают буквально случайные числа. Вместо этого они возвращают строку символов, используя случайные числа для выбора из доступных наборов символов. Вы всегда должны разрешать использование всех доступных наборов символов, если только вы не создаёте пароль для сайта, который не допускает использование специальных символов.
Набор доступных латинских символов включает в себя 26 заглавных букв, 26 строчных букв и 10 цифр. Он также включает в себя набор специальных символов, который у разных генераторов может быть разным. Предположим, что доступно 18 специальных символов. В итоге получается выбор из 80 символов. В полностью случайном пароле есть 80 вариантов для каждого символа. Если вы выберете восьмизначный пароль, количество возможных вариантов составит 80 в 8 степени, или 1 677 721 600 000 000 — больше квадриллиона. Это сложная задача для взлома методом перебора, а угадывание методом перебора — единственный способ взломать действительно случайный пароль.
Полностью случайный генератор иногда может выдавать пароль вроде «аааааааа», «Covfefe!» и «12345678», поскольку они так же вероятны, как и любая другая последовательность из восьми символов. Некоторые генераторы паролей фильтруют вывод, чтобы избежать таких паролей. Это нормально, но если хакер знает об этих фильтрах, это уменьшает количество возможностей и упрощает взлом методом перебора.
Рассмотрим пример. Существует 40 960 000 возможных четырёхсимвольных паролей, взятых из набора из 80 символов. Но некоторые генераторы паролей принудительно выбирают хотя бы по одному символу каждого типа, и это резко снижает количество вариантов. Есть 80 вариантов для первого символа. Предположим, это заглавная буква; набор для второго символа — 54 (80 минус 26 заглавных букв). Далее предположим, что второй символ — это строчная буква. Для третьего символа остаются только цифры и специальные символы из 28 вариантов. И если третий символ знак препинания, последний должен быть цифрой, то есть 10 вариантов. 40 млн возможностей сокращаются до 1 209 600.
Использование всех наборов символов не является необходимостью на многих сайтах. Чтобы это требование не привело к сокращению вариантов паролей, установите большую длину пароля. Когда пароль достаточно длинный, эффект навязывания разных типов символов становится незначительным.
Другие ограничения в менеджерах паролей тоже сокращают набор возможных паролей. Например, RememBear Premium указывает точное количество символов каждого из четырёх наборов символов, что резко сокращает пул. По умолчанию для этого требуются две заглавные буквы, две цифры, 14 строчных букв и никаких символов, всего 18 символов. Это приводит к тому, что пул паролей в сотни миллионов раз меньше, чем если бы он просто требовал одного или нескольких символов каждого типа. Проблема снова решается созданием более длинного пароля.
Как не обломать мозг об пароли вроде eLkdC,lk#jB
Нормальный стойкий пароль фиг запомнишь. Почти аксиома. Еще и безопасники радостно подбрасывают дровишек в этот костер ужаса, заставляя раз в месяц учить чудовищный фарш из мешанины символов. Параноидальные меры безопасности в лучших традициях «Хакера в столовой» приводят лишь к тому, что пользователи заботливо царапают пароли на мониторе или складывают под клавиатуру. Нет, серьезно, ну кто из обычных пользователей в здравом уме будет соблюдать требования к паролю в духе:
Энтропия
Классические пароли становятся более сложными для запоминания человеком и все более легкими в подборе для машины. Это прискорбно. На очередном очень важном и секьюрном сайте с кулинарными рецептами от вас требуют десятизначный пароль во всех регистрах и с цифрами? Тут могут быть три причины.
Сложность пароля в компьютерной индустрии обычно оценивают в терминах информационной энтропии (понятие из теории информации), измеряемой в битах. Вместо количества попыток, которые необходимо предпринять для угадывания пароля, вычисляется логарифм по основанию 2 от этого числа, и полученное число называется количеством «битов энтропии» в пароле. Пароль со, скажем, 42-битной сложностью, посчитанной таким способом, будет соответствовать случайно сгенерированному паролю длиной в 42 бита. Другими словами, чтобы методом полного перебора найти пароль с 42-битной сложностью, необходимо создать 2 42 паролей и попытаться использовать их; один из 2 42 паролей окажется правильным. Согласно формуле при увеличении длины пароля на один бит количество возможных паролей удвоится, что сделает задачу атакующего в два раза сложнее. В среднем атакующий должен будет проверить половину из всех возможных паролей до того, как найдет правильный.
Википедия
Количественная оценка стойкости парольной защиты
Автор работы: Пользователь скрыл имя, 26 Декабря 2010 в 11:08, контрольная работа
Краткое описание
Цель работы – реализация простейшего генератора паролей, обладающего требуемой стойкостью к взлому.
Задание на контрольную работу
1. В таблице 1 найти для 15-го варианта значения характеристик P,V,T.
2. Вычислить по формуле (1) нижнюю границу S* для заданных P,V,T.
3. Выбрать некоторый алфавит с мощностью A и получить минимальную длину пароля L, при котором выполняется условие (2).
Содержание
Введение…………………………………………………………………………… 3
1. Теоретическая часть
1.1. Определение стойкости подсистемы идентификации и аутентификации 4
1.2. Минимальные требования к паролю……………………………………… 4
1.3. Минимальные требования к подсистеме парольной аутентификации…. 4
1.4. Определение вероятности подбора пароля злоумышленником в течении срока действия пароля………………………………………………… 5
1.5. Выбором каким параметров можно повлиять на уменьшение вероятности подбора пароля злоумышленником при заданной скорости подбора пароля злоумышленником и заданном сроке действия пароля……. 5
2. Практическая часть
2.1. Исходный код программы……………………………………………………. 6
2.2. Примеры паролей…………………………………………………………….. 7
2.3. Скриншоты программы………………………………………………………. 7
Вложенные файлы: 1 файл
КонрабИнформационная безопасность.doc
Международный «ИНСТИТУТ УПРАВЛЕНИЯ»
Северодвинский центр дистанционного образования
По теме: Количественная оценка стойкости парольной защиты.
Студент: Шестаков А.И.
Преподаватель : Широкая Е. А.
Цель работы – реализация простейшего генератора паролей, обладающего требуемой стойкостью к взлому.
Задание на контрольную работу
1. В таблице 1 найти для 15-го варианта значения характеристик P,V,T.
2. Вычислить по формуле (1) нижнюю границу S* для заданных P,V,T.
3. Выбрать некоторый алфавит с мощностью A и получить минимальную длину пароля L, при котором выполняется условие (2).
Реализовать программу – генератор паролей пользователей. Программа должна формировать случайную последовательность символов длины L, при этом должен использоваться алфавит из A символов.
Целочисленное значение нижней границы вычисляется по формуле:
1. Теоретическая часть
1.1 Определение стойкости подсистемы идентификации и аутентификации.
Стойкость подсистемы идентификации и аутентификации пользователя в системе защиты информации (СЗИ) во многом определяет устойчивость к взлому самой СЗИ. Данная стойкость определяется гарантией того, что злоумышленник не сможет пройти аутентификацию, присвоив чужой идентификатор или украв его.
1.2 Минимальные требования к выбору пароля.
Основными минимальными требованиями к выбору пароля являются следующие:
— Минимальная длина пароля должна быть не менее 6 символов.
— Пароль должен состоять из различных групп символов (малые и большие латинские буквы, цифры, специальные символы ‘(’, ‘)’, ‘#’ и т.д.).
— В качестве пароля не должны использоваться реальные слова, имена, фамилии и т.д.
1.3 Минимальные требования к подсистеме парольной аутентификации.
Основными минимальными требованиями к подсистеме парольной аутентификации пользователя являются следующие.
— Администратор СЗИ должен устанавливать максимальный срок действия пароля, после чего, он должен быть сменен.
— В подсистеме парольной аутентификации должно быть установлено ограничение числа попыток ввода пароля (как правило, не более 3).
— В подсистеме парольной аутентификации должна быть установлена временная задержка при вводе неправильного пароля.
1.4 Определение вероятности подбора пароля злоумышленником в течении срока действия пароля.
Вероятность P подбора пароля злоумышленником в течении срока его действия V определяется по следующей формуле.
— число всевозможных паролей длины L, которые можно составить из символов алфавита A;
V – скорость перебора паролей злоумышленником;
T – максимальный срок действия пароля.
1.5 Выбором каких параметров можно повлиять на уменьшение вероятности подбора пароля злоумышленником при заданной скорости подбора пароля злоумышленником и заданном сроке действия пароля.
Выбор следующих параметров влияет на уменьшение вероятности подбора пароля:
— L – длина пароля (должна быть более 6 символов).
2. Практическая часть
Целочисленное значение нижней границы вычисляется по формуле:
После нахождения нижней границы S* необходимо выбрать такие A и L где, A – мощность алфавита паролей, L – длина пароля, чтобы выполнялось неравенство:
В данном случае удовлетворяют такие комбинации A и L, как A=27, L=8 (пароль состоит из 8 символов, среди которых могут быть малые латинские буквы).
В качестве алфавита символов, используемых при генерации пароля, был выбран следующий набор – 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q. Мощность данного набора A= 27.
2.1. Исходный код программы :
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure TForm1.Button2Click(Sender: TObject);
procedure TForm1.FormCreate(Sender: TObject);
function RandomPwd(PWLen: integer): string;
const StrTable: string =’aol1b2c3md4pe5nf6qg7h8i9j0k’ ;
if (PWlen > Length(StrTable)) then
if (pos(StrTable[X], result) = 0) then begin
procedure TForm1.Button1Click(Sender: TObject);
Разбор алгоритмов генерации псевдослучайных чисел
Я работаю программистом в игровой студии IT Territory, а с недавних пор перешел на направление экспериментальных проектов, где мы проверяем на прототипах различные геймплейные гипотезы. И работая над одним из прототипов мы столкнулись с задачей генерации случайных чисел. Я хотел бы поделиться с вами полученным опытом: расскажу о псевдогенераторах случайных чисел, об альтернативе в виде хеш-функции, покажу, как её можно оптимизировать, и опишу комбинированные подходы, которые мы применяли в проекте.
Случайными числами пользовались с самого зарождения математики. Сегодня их применяют во всевозможных научных изысканиях, при проверке математических теорем, в статистике и т.д. Также случайные числа широко используются в игровой индустрии для генерирования 3D-моделей, текстур и целых миров. Их применяют для создания вариативности поведения в играх и приложениях.
Есть разные способы получения случайных чисел. Самый простой и понятный — это словари: мы предварительно собираем и сохраняем набор чисел и по мере надобности берём их по очереди.
К первым техническим способам получения случайных чисел можно отнести различные генераторы с использованием энтропии. Это устройства, основанные на физических свойствах, например, емкости конденсатора, шуме радиоволн, длительности нажатия на кнопку и так далее. Хоть такие числа действительно будут случайными, у таких способов отсутствует важный критерий — повторяемость.

Сегодня мы с вами поговорим о генераторах псевдослучайных чисел — вычисляемых функциях. К ним предъявляются следующие требования:
Длинный период. Любой генератор рано или поздно начинает повторяться, и чем позже это случится, тем лучше, тем непредсказуемее будет результат.
Портируемость алгоритма на различные системы.
Скорость получения последовательности. Чем быстрее, тем лучше.
Повторяемость результата. Это очень важный показатель. От него зависят все компьютерные игры, которые используют генераторы миров и различные системы с аналогичной функциональностью. Воспроизводимость даёт нам общий контент для всех, то есть мы можем генерировать на отдельных клиентах одинаковое содержимое. Также мы можем генерировать контент на лету в зависимости от входных данных, например, от местоположения игрока в мире. Ещё повторяемость случайных чисел используется для сохранения конкретного контента в виде зерна. То есть мы можем держать у себя только какое-то число или массив чисел, на основе которых будут генерироваться нужные нам параметры для заранее отобранного контента.
Зерно
Зерно — это основа генерирования. Оно представляет собой число или вектор чисел, который мы отправляем при инициализации генератора.
Решить эту проблему можно будет с помощью разделения одного генератора на несколько отдельных.
То есть берём несколько генераторов и задаём им разные зёрна. Но тут мы можем столкнуться со второй проблемой: нельзя гарантировать случайность i-тых элементов разных последовательностей с разными зёрнами.

На иллюстрации изображён результат генерирования нулевого элемента последовательности с помощью стандартной библиотекой C#. Мы постепенно меняли зерно от 0 до N.
Качество генератора
Предлагаю оценивать качество генератора с помощью изображений разного типа. Первый тип — это просто сгенерированная последовательность, который мы визуализируем с помощью первых трёх байтов полученного числа, конвертированных в RGB-представление.
Второй тип изображений — это пространственная интерпретация сгенерированной последовательности. Мы берём первые два бита числа (Х и Y), затем считаем количество попаданий в заданные точки и при визуализации вычитаем из 1 отношение количества попаданий в конкретный пиксель к максимальному количеству попаданий в какой-то другой пиксель. Черные пиксели — это точка, куда мы попадаем чаще всего, а белые — куда мы либо почти, либо совсем не попали.
Сравнение генераторов
Стандартные средства C#
Ниже я сравнил стандартный генератор из библиотеки С# и линейную последовательность. Первый столбец слева — это случайная последовательность от 0 до N в рамках одного зерна. В центре вверху показаны нулевые элементы случайных последовательностей при разных зёрнах от 0 до N. Вторая линейная последовательность — это числа от 0 до N, которые я визуализировал нашим алгоритмом.
В рамках одного зерна генератор действительно создаёт случайное число. Но при этом для i-тых элементов последовательностей с разным зерном прослеживается паттерн, который схож с паттерном линейной последовательности.
Линейный конгруэнтный генератор (LCG)
Давайте рассмотрим другие алгоритмы. Деррик Генри в 1949 году создал линейный конгруэнтный генератор, который подбирает некие коэффициенты и с их помощью выполняет возведения в степень со сдвигом.
При генерировании с одним зерном паттерн нигде не образуется. Но при использовании i-тых элементов в последовательностях с различными зёрнами паттерн начинает прослеживаться. Причём его вид будет зависеть исключительно от коэффициентов, которые мы подобрали для генератора. Например, есть частный случай линейного конгруэнтного генератора — Randu.
XorShift
Давайте теперь посмотрим на более свежую разработку — XorShift. Этот алгоритм просто выполняет операцию Xor и сдвигает байт в несколько раз. У него тоже будет прослеживаться паттерн для i-тых элементов последовательностей.
Вихрь Мерсенна
Неужели не существует генераторов без паттерна? Такой генератор есть — это вихрь Мерсенна. У этого алгоритма очень большой период, из-за чего появление паттерна на некотором количестве чисел физически невозможно. Однако и сложность этого алгоритма достаточно велика, в двух словах его не объяснить.
Unity — Random
Из других разработок стоит упомянуть генератор от компании Unity — Random, который используется в наборе стандартных библиотек для работы с Unity. При использовании первых элементов последовательности для разных зёрен у него будет прослеживаться паттерн, но при увеличении индекса паттерн исчезает и получается действительно случайная последовательность.
Перемешанный конгруэнтный генератор (PCG)
Противоположностью юнитёвского Random’a является перемешанный конгруэнтный генератор. Его особенность в том, что для первых элементов с различными зёрнами отсутствует ярко выраженный паттерн. Но при увеличении индекса он всё же возникает.
Длительность последовательного генерирования
Это важная характеристика генераторов. В таблице приведена длительность для алгоритмов в миллисекундах. Замеры проводились на моём MacBook Pro 2019 года.
0 seed 0..n
100 seed 0..n
Вихрь Мерсенна работает дольше всего, но даёт качественный результат. Стандартный генератор Random из библиотеки C# подходит для задач, в которых случайность вторична и не имеет какой-то значимой роли, то есть его можно использовать в рамках одного зерна. LCG (линейный конгруэнтный генератор) — это уже более серьёзный алгоритм, но требуется время на подбор нужных коэффициентов, чтобы получить адекватный паттерн. XorShift — самый быстрый алгоритм из всех рассмотренных. Его можно использовать там, где нужно быстро получить случайное значение, но помните про ярко выраженный паттерн с повторяющимся значением. Unity Random и PCG (перемешанный конгруэнтный генератор) сопоставимы по длительности работы, поэтому в разных ситуациях мы можем менять их местами: для длительных последовательностей использовать Unity, а для коротких — PCG.
Альтернатива генераторам — хеш-функции
Хеш-функции (функции свёртки) по определённому алгоритму преобразуют массив входных данных произвольной длины в строку заданной длины. Они позволяют быстрее искать данные, это свойство используется в хеш-таблицах. Также для хеш-функций характерна равномерность распределения, так называемый лавинный эффект. Это означает, что изменение малого количества битов во входном тексте приведёт к лавинообразному и сильному изменению значений выходного массива битов. То есть все выходные биты зависят от каждого входного бита.
Требования к генераторам на основе хеш-функций предъявляются те же самые, что и к простым генераторам, кроме длительности получения последовательности. Дело в том, что такому генератору можно отправить на вход одновременно зерно и требуемое состояние, потому что хеш-функции принимают на вход массивы данных.
Вот пример использования хеш-функции: можно либо создать конкретный класс, отправить туда зерно и постепенно запрашивать только конкретные состояния, либо написать статичную функцию, и отправить туда сразу и зерно, и конкретное состояние. Слева показан алгоритм работы MD5 из стандартной библиотеки C#.

Сделать генератор на основе хеш-функции можно так. Непосредственно при инициализации генератора задаём зерно, увеличиваем счётчик на 1 при запросе следующего значения и выводим результат хеша по зерну и счётчику.
Одни из самых популярных хеш-функций — это MurMur3 и WangHash.
MurMur3 не создаёт паттернов при использованиии i-тых элементов разных последовательностей при разных зёрнах. У WangHash статистические показатели образуют заметный паттерн. Но любую функцию можно прогнать через себя два раза и получить улучшенные показатели, как это показано в правом крайнем столбце WangDoubleHash.
Также сегодня активно развивается и набирает популярность алгоритм xxHash.
Забегая вперёд, скажу, что мы выбрали этот генератор для наших проектов и активно его используем.
Длительность последовательного генерирования у всех хеш-функций примерно одинакова. Однако у MD5 эта характеристика заметно отличается, но не потому, что алгоритм плохой, а потому что в стандартной реализации MD5 много разных состояний, которые влияют на быстродействие алгоритма.