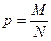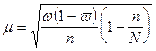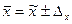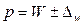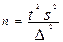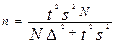что понимается под выборочным методом

Статистические исследования являются весьма трудоемким и дорогим способом достижения определенных научных результатов. Именно поэтому возникла мысль использовать выборочное наблюдение вместо сплошного. Основной целью его является отражение характеристик статистической совокупности, которая подлежит изучению, по обследованной части. В данной статье рассмотрим понятие, особенности и виды наблюдения, существующие на сегодняшний день.

Понятие

Выборочное наблюдение – это наблюдение, основанное на методике статистического исследования, в соответствии с которым установление обобщающих показателей совокупности осуществляется лишь по отдельно взятой части. Причем базой в данном случае служат определенные положения выбора в случайном порядке. Выборочный метод предполагает изучение исключительно некоторой части всей совокупности. Важно отметить, что статистическая совокупность, подлежащая исследованию, именуется генеральной. Проведение выборочного наблюдения предполагает наличие выборочной совокупности, которая по-другому называется выборкой. Ее следует рассматривать как часть единиц, отобранную из генеральной совокупности, которая принимает участие в исследовании статистического характера.

Значение методики

Стоит отметить, что выборочное наблюдение – это наблюдение, которое наделяется определенным значением. Оно состоит в том, что при минимальном количестве исследуемых единиц осуществление исследования по статистике пройдет за предельно короткий период времени. При этом затраты труда и средств также будут минимальны. Необходимо дополнить, что в генеральной совокупности часть единиц, обладающая изучаемым признаком, именуется генеральной долей (обозначается она буквой р). Средняя величина исследуемого варьирующего признака называется генеральной средней и обозначается буквой х.

Выборочные статистические наблюдения строятся на основе совокупностей, в которых долю рассматриваемого признака именуют выборочной частью или долей и обозначают буквой w. Среднюю величину в выборке называют выборочной средней.

Результаты исследований

Необходимо знать, что результаты выборочного наблюдения могут быть достаточно точными. Здесь стоит лишь соблюдать все правила научной организации исследования. Именно поэтому изучаемую методику целесообразно использовать для проверки информации, полученной из наблюдения сплошного типа. Важно дополнить, что выборочное наблюдение – это наблюдение, получившее предельно широкое распространение во вневедомственной и государственной статистике. Причина тому – минимальное количество единиц, участвующих в исследовании, что позволяет провести его точно и тщательно.

Совокупность статистического характера включает в себя единицы, наделенные варьирующими признаками. Следует знать, что состав выборки может несколько отличаться от состава генеральной совокупности. Именно это расхождение между свойствами генеральной и выборочной совокупности является ошибкой выборочного наблюдения.

Ошибки выборки

Важно отметить, что ошибки, которые свойственны несплошному наблюдению, в первую очередь характеризуют величину расхождения между информацией, полученной из всей совокупности и выборочного исследования. Недочеты, появляющиеся в процессе выборочных статистических наблюдений, именуются ошибками репрезентативности. Необходимо дополнить, что они классифицируются на систематические и случайные.

Как выяснилось, выборочное наблюдение – это наблюдение, которому в некоторые случаях свойственны ошибки. Так, если выборка недостаточно четко воспроизводит целую совокупность по причине выборочного характера наблюдения, то речь идет о случайных ошибках. Стоит дополнить, что их размеры можно определить с достаточной степенью точности на базе теории вероятности и закона больших чисел. Систематические ошибки в выборочном методе наблюдения появляются при нарушении принципа, связанного со случайностью выбора единиц совокупности для исследования. На сегодняшний день в практической деятельности распространены как случайные, так и систематические ошибки в равной степени.

Классификация категории

Далее целесообразно разобрать существующие в настоящее время виды выборочного наблюдения. Так, в соответствии со способом формирования (методикой отбора) выборки определенного количества единиц из генеральной совокупности распространенными являются следующие разновидности выборочного характера наблюдения:

Целесообразно рассмотреть каждую из представленных разновидностей выборочного наблюдения в статистике по отдельности.

Простая и типическая выборка

Под собственно-случайной (иными словами, простой) выборочной совокупностью следует понимать отбор единиц из генерального вида совокупности посредством случайного отбора. Однако при этом должна присутствовать вероятность выбора абсолютно любой единицы из общей совокупности. Стоит отметить, что данная разновидность отбора производится с помощью методики жеребьевки или с использованием таблицы случайных чисел.

Стратифицированная выборочная совокупность, которую по-другому именуют типической, так или иначе подразумевает деление генеральной совокупности, носящей неоднородный характер, на районированные типологические группировки по тому или иному значительному признаку. После этого из каждой группы случайным образом отбирается некоторое количество единиц.

Серийная и механическая выборка

Необходимо знать, что для гнездовой выборки, которую по-другому именуют серийной, характерно то, что общая совокупность изначально делится на определенные неравновеликие или равновеликие серии – единицы внутри одной серии связаны в соответствии с определенным признаком, – из которых посредством случайного отбора выбираются конкретные серии, после чего внутри данных серий осуществляется наблюдение сплошного типа.

Под механической выборкой следует понимать отбор единиц посредством равных промежутков, другими словами, через временные промежутки, по алфавиту, в соответствии с пространственным способом и так далее. При реализации механического отбора общая совокупность так или иначе делится на равные по количеству группировки, из которых в дальнейшем отбирается строго по одной единице.

Комбинированная и многоступенчатая выборка

Комбинированная выборочная совокупность базируется, главным образом, на сочетании нескольких методик выборки. Многоступенчатая совокупность же предполагает формирование внутри генеральной сначала крупных группировок единиц, из которых создаются меньшие по объему группы. Так происходит до тех пор, пока отобранными не оказываются те группировки или отдельные единицы, которые подлежат исследованию.

Повторный и бесповторный объем

Помимо представленной выше классификации важно указать то, что выборочный тип отбора бывает повторным и бесповторным. В случае повторного отбора вероятность выбора той или иной единицы никаким образом не ограничивается. При бесповторном же отборе избранная единица не возвращается в исходную совокупность.

Стоит отметить, что для отобранных единиц совокупности рассчитываются показатели обобщенного характера (относительные или средние). В дальнейшем результаты исследования выборочного плана распространяются на генеральную совокупность в целом. Нужно дополнить, что ключевой задачей проведения выборочного исследования служит выявление ошибок выборки. Так, принято классифицировать ошибки на среднюю и предельную. Они имеют принципиальное отличие и зависят от целого ряда факторов. Среди них стоит отметить следующие пункты:

Распространение выборочного наблюдения на генеральную совокупность

Далее целесообразно рассмотреть известные на сегодняшний день методики распространения наблюдения характера выборки на генеральную совокупность. Речь идет о способе коэффициентов и прямом пересчете. Под последним следует понимать произведение среднего значения определенного признака на весь объем известной генеральной совокупности. Стоит знать, что большое количество факторов не позволяет полноценным образом применить точечную оценку пересчета прямого типа при распространении результатов выборочной совокупности на генеральную. В практической деятельности чаще всего используют интервальную оценку. Именно она позволяет в полной мере учитывать размер предельной ошибки выборочной совокупности, рассчитанной для средней или же для части признака.

Способ коэффициентов в настоящее время применяется тогда, когда наблюдение характера выборки осуществляется с целью уточнения и проверки информации, полученной по результатам сплошного наблюдения. Так, численность совокупности с определенной поправкой на недоучет определяется как произведение численности совокупности без данной поправки и дроби, в числителе которой – численность совокупности по информации из контрольных мероприятий в тех же точках, а в знаменателе – численность совокупности без поправки на недоучет.

Если необходимо уточнить сведения сплошного наблюдения при реализации контроля за исследованиями выборочного характера, нужно выявить поправку на недоучет. Следует заметить, что методика расчета данной поправки на сегодняшний день достаточно широко используется в случае исследования небольших по размерам совокупностей. Именно тогда можно рассчитать коэффициент недоучета по абсолютно каждой категории сотрудников и, уточнив актуальную информацию, распространить полученных результаты на совокупность в целом.

Здесь целесообразно привести пример. Так, при осуществлении сплошного учета гаражей в городе насчитывалось 1000 гаражей, которые зарегистрированы по южному району, 750 единиц – по северному, 400 – по восточному. В соответствии с контрольными мероприятиями было определено следующее количество гаражей:

Таким образом, с помощью формулы способа коэффициентов (или применяя заранее определенный коэффициент при учете выборочного плана) можно получить количество гаражей после контроля, которое обозначим буквой У, с поправкой на недоучет:

У(Ю) = 1000 210 : 200 = 1050; У(С) = 750 160 : 150=800;

У(В) = 400 110 : 100 = 440.

Заключение

Итак, мы рассмотрели понятие, виды, характеристику и основные особенности категории выборочного наблюдения, а также привели соответствующие примеры и расчеты. В заключение следует отметить, что на базе метода коэффициентов, рассмотренного в предыдущей главе, проверка результатов наблюдения сплошного типа предельно широко используется в экономической и социальной статистике. Например, сюда относится контроль за коммерческой деятельностью физических и юридических лиц со стороны финансовых структур.

Источник

Основы выборочного метода

Статистическое исследование может осуществляться по данным несплошного наблюдения, основная цель которого состоит в получении характеристик изучаемой совокупности по обследованной ее части. Одним из наиболее распространенных в статистике методов, применяющих несплошное наблюдение, является выборочный метод.

Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора.

Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.

Преимущества выборочного наблюдения заключаются в существенной экономии различного вида ресурсов, а именно:

• финансовых средств, затрачиваемых на сбор и обработку данных, подготовку и оплату кадров;

• материально-технических ресурсов (канцелярские товары, оргтехника, расходные материалы, транспортное обслуживание и т.п.),

• трудовых ресурсов, привлекаемых к обследованию на всех его этапах;

• времени, затрачиваемого как на получение первичной информации, так и на последующую ее обработку, вплоть до публикации итоговых материалов.

В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка сопровождается уничтожением или разложением на составные части обследуемых образцов

При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью.Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью или просто выборкой.

В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей (обозначается р), а средняя величина изучаемого варьирующего признака — генеральной средней (обозначается ).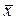

Генеральная доля определяется из отношения единиц генеральной совокупности, обладающих изучаемым признаком М, к общей численности единиц генеральной совокупности N:

В выборочной совокупности долю изучаемого признака называют выборочной долей (обозначается ), а среднюю величину в выборке — выборочной средней (обозначается ).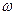

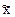
Выборочная доля 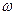определяется из отношения единиц, обладающих изучаемым признаком m, к общей численности единиц выборочной совокупности n:

Отбор единиц в выборочную совокупность может быть повторным или бесповторным. При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения. Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется. На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.

При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.

Ошибки выборки

Ошибки выборочного наблюдения, которые иначе называют ошибками репрезентативности, возникают вследствие специфики самого метода и именно потому, что обследуется не вся совокуп­ность, а лишь его часть, отобранная в случайном порядке.

Определение средней величины этих ошибок и их возможных границ, а следовательно, определение достоверности данных выбо­рочного наблюдения, является основной задачей теории выборочно­го исследования.

Ошибка выборки— это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.

Теория и практика применения выборочного метода показали, что данные выборочного наблюдения достаточно достоверны, так как выборочный метод базируется на применении закона больших чисел и теории вероятности. Сущность закона больших чисел за­ключается втом, что чем больше будет взято единиц подна­блюдение, тем точнее средняя выборочная будет воспроизводить среднюю генеральную.

Теория выборочного метода дает формулу, по которой можно вычислить среднюю величину ошибки для выборочной совокупности, отобранной в случайном порядке, т.е. таким образом, что каждая единица генеральной совокупности имела бы равную возможность попасть в это число.

Определение ошибкивыборочной средней:

1). При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:

,

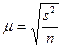
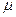
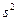
где — средняя ошибка выборочной средней;

— дисперсия выборочной совокупности;

n — численность выборки.

2). При бесповторном отборе она рассчитывается по формуле:

,

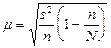
где N — численность генеральной совокупности.

Величина средней ошибки выборки зависит прежде всего от показателей колеблемости значений признаков в выборочной совокупности. Степень колеблемости значений признаков определяется средним квадратическим отклонением.

Чем меньше величина среднего квадратического отклонения (следовательно, чем однороднее совокупность), тем меньше вели­чина средней ошибки при той же численности выборки.

Кроме того, величина средней ошибки зависит от численности выборки. Увеличивая или уменьшая объем выборки, можно регу­лировать величину ошибки. Чем больше единиц будет охвачено выборочным наблюдением, тем меньше будет величина ошибки, так как тем точнее будет представлена генеральная совокупность. По­лученная величина ошибки характеризует среднее отклонение средней выборочной от средней генеральной.

Определение ошибки выборочной доли:

1). При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

,

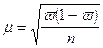
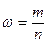
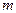
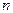
где — выборочная доля единиц, обладающих изучаемым признаком;

— число единиц, обладающих изучаемым признаком;

— численность выборки.

2). При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:

На практике при применении выборочного метода обычно ставится задача определения пределов, за которые не выйдетвели­чина конкретной ошибки выборочного наблюдения.

Величина пределов конкретной ошибки зависит от степе­ни вероятности, с которой измеряется ошибка выборки.

Ошибка выборки, исчисленная с заданной степенью вероятности, представляет предельную ошибку выборки.

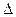
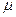
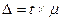
Предельная ошибка выборки связана со средней ошибкой выборки отношением:

.

При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.

Величину вероятности для различных значений t можно определить на основе теоремы Ляпунова. На практике пользуются готовыми таблицами значений этой функции, вычисленных для различных значений t. С увеличением значения t вероятность Р быстро приближается к единице, так что практически обычно ограничиваются значениями t, не превышающими 2—3 единицы:

Уже при значении t, равном 3, вероятность очень близка к единице. Это означает, что если бы из одной и той же генеральной совокупности было произведено большое число случайных выборок одинаковой численности, то в среднем на 1000 выборок приходилось бы 997 таких, в которых отклонение выборочной средней от генеральной не превышало бы 3 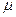, и только в трех выборках отклонение могло бы выйти за эти пределы.

Указывая вероятные пределы случайной ошибки выборки, мы тем самым указываем и те пределы, за которые не выйдет характеристика генеральной совокупности, т.е. решаем ту задачу, которая, собственно, и ставится при выборочном наблюдении.

Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:

,

.

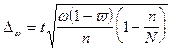
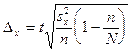
Предельная ошибка выборки при повторном отборе определяется по формуле:

,

.

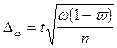
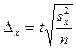
Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:

для средней

для доли

Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения. Чем больше объем выборки, тем меньше значения средней и предельной ошибок выборочного наблюдения и, следовательно, тем уже границы генеральной средней и генеральной доли. В то же время необходимо учитывать, что большой объем выборки приводит к удорожанию обследования, увеличению сроков сбора и обработки материалов, требует привлечения дополнительного персонала и соответствующего материально-технического обеспечения. Поэтому при подготовке выборочного наблюдения необходимо определить тот минимально необходимый объем выборки, который обеспечит требуемую точность полученных статистических характеристик при заданном уровне вероятности.

Необходимый объем повторной выборки при определении средней величины может быль рассчитан по формуле:

а объем бесповторной выборки:

Численность повторной выборки при изучении доли определяется следующим образом:

Источник