что порождает электромагнитное поле
Электромагнитное поле
 Классическая электродинамика Классическая электродинамика | ||||||||||||
 | ||||||||||||
| Электричество · Магнетизм | ||||||||||||
| ||||||||||||
| См. также: Портал:Физика |
Электромагни́тное по́ле — фундаментальное физическое поле, взаимодействующее с электрически заряженными телами, а также с телами, имеющими собственные дипольные и мультипольные электрические и магнитные моменты. Представляет собой совокупность электрического и магнитного полей, которые могут, при определённых условиях, порождать друг друга, а по сути являются одной сущностью, формализуемой через тензор электромагнитного поля.
Электромагнитное поле (и его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла. При переходе от одной инерциальной системы отсчета к другой электрическое и магнитное поле в новой системе отсчета — каждое зависит от обоих — электрического и магнитного — в старой, и это ещё одна из причин, заставляющая рассматривать электрическое и магнитное поле как проявления единого электромагнитного поля.
В современной формулировке электромагнитное поле представлено тензором электромагнитного поля, компонентами которого являются три компонента напряжённости электрического поля и три компонента напряжённости магнитного поля (или — магнитной индукции) [
Действие электромагнитного поля на заряженные тела описывается в классическом приближении посредством силы Лоренца.
Квантовые свойства электромагнитного поля и его взаимодействия с заряженными частицами (а также квантовые поправки к классическому приближению) — предмет квантовой электродинамики, хотя часть квантовых свойств электромагнитного поля более или менее удовлетворительно описывается упрощённой квантовой теорией, исторически возникшей заметно раньше.
Возмущение электромагнитного поля, распространяющееся в пространстве, называется электромагнитной волной (электромагнитными волнами) [
Содержание
История открытия
До начала XIX в. электричество и магнетизм считались явлениями, не связанными друг с другом, и рассматривались в разных разделах физики.
В 1819 г. датский физик Г. Х. Эрстед обнаружил, что проводник, по которому течёт электрический ток, вызывает отклонение стрелки магнитного компаса, расположенного вблизи этого проводника, из чего следовало, что электрические и магнитные явления взаимосвязаны.
Французский физик и математик А. Ампер в 1824 г. дал математическое описание взаимодействия проводника тока с магнитным полем (см. Закон Ампера).
В 1831 г. английский физик М. Фарадей экспериментально обнаружил и дал математическое описание явления электромагнитной индукции — возникновения электродвижущей силы в проводнике, находящемся под действием изменяющегося магнитного поля.
В 1864 г. Дж. Максвелл создаёт теорию электромагнитного поля, согласно которой электрическое и магнитное поля существуют как взаимосвязанные составляющие единого целого — электромагнитного поля. Эта теория с единой точки зрения объясняла результаты всех предшествующих исследований в области электродинамики, и, кроме того, из неё вытекало, что любые изменения электромагнитного поля должны порождать электромагнитные волны, распространяющиеся в диэлектрической среде (в том числе, в пустоте) с конечной скоростью, зависящей от диэлектрической и магнитной проницаемости этой среды. Для вакуума теоретическое значение этой скорости было близко к экспериментальным измерениям скорости света, полученным на тот момент, что позволило Максвеллу высказать предположение (впоследствии подтвердившееся), что свет является одним из проявлений электромагнитных волн.
Теория Максвелла уже при своем возникновении разрешила ряд принципиальных проблем электромагнитной теории, предсказав новые эффекты и дав надежную и эффективную математическую основу описанию электромагнитных явлений. Однако при жизни Максвелла наиболее яркое предсказание его теории — предсказание существования электромагнитных волн — не получило прямых экспериментальных подтверждений.
В 1887 г. немецкий физик Г. Герц поставил эксперимент, полностью подтвердивший теоретические выводы Максвелла. Его экспериментальная установка состояла из находящихся на некотором расстоянии друг от друга передатчика и приёмника электромагнитных волн, и фактически представляла собой исторически первую систему радиосвязи, хотя сам Герц не видел никакого практического применения своего открытия, и рассматривал его исключительно как экспериментальное подтверждение теории Максвелла.
В XX в. развитие представлений об электромагнитном поле и электромагнитном излучении продолжилось в рамках квантовой теории поля, основы которой были заложены великим немецким физиком Максом Планком. Эта теория, в целом завершенная рядом физиков около середины XX века, оказалась одной из наиболее точных физических теорий, существующих на сегодняшний день.
Во второй половине XX века (квантовая) теория электромагнитного поля и его взаимодействия была включена в единую теорию электрослабого взаимодействия и ныне входит в так называемую стандартную модель в рамках концепции калибровочных полей (электромагнитное поле является с этой точки зрения простейшим из калибровочных полей — абелевым калибровочным полем).
Классификация
Электромагнитное поле с современной точки зрения есть безмассовое [
Среди известных (не гипотетических) фундаментальных полей электромагнитное поле — единственное, относящееся к указанному типу. Все другие поля такого же типа (которые можно рассматривать, по крайней мере, чисто теоретически) — (были бы) полностью эквивалентны электромагнитному полю, за исключением, быть может, констант.
Физические свойства
В рамках квантовой электродинамики электромагнитное излучение можно рассматривать как поток фотонов. Частицей-переносчиком электромагнитного взаимодействия является фотон (частица, которую можно представить как элементарное квантовое возбуждение электромагнитного поля) — безмассовый векторный бозон. Фотон также называют квантом электромагнитного поля (подразумевая, что соседние по энергии стационарные состояния свободного электромагнитного поля с определенной частотой и волновым вектором различаются на один фотон).
Электромагнитное взаимодействие — это один из основных видов дальнодействующих фундаментальных взаимодействий, а электромагнитное поле — одно из фундаментальных полей.
Существует теория (входящая в Стандартную модель), объединяющая электромагнитное и слабое взаимодействие в одно — электрослабое. Также существуют теории, объединяющие электромагнитное и гравитационное взаимодействие (например, теория Калуцы-Клейна). Однако последняя, при её теоретических достоинствах и красоте, не является общепринятой (в смысле её предпочтительности), так как экспериментально не обнаружено ее отличий от простого сочетания обычных теорий электромагнетизма и гравитации, как и теоретических преимуществ в степени, заставившей бы признать её особенную ценность. Это же (в лучшем случае) можно сказать пока и о других подобных теориях: даже лучшие из них по меньшей мере недостаточно разработаны, чтобы считаться вполне успешными.
Безопасность электромагнитных полей
Контроль за уровнями ЭМП возложен на органы санитарного надзора и инспекцию электросвязи, а на предприятиях — на службу охраны труда.
Электромагнитное поле
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электромагнитное поле.
Вспомним, каким образом Максвелл объяснил явление электромагнитной индукции. Переменное магнитное поле порождает вихревое электрическое поле. Если в переменном магнитном поле находится замкнутый проводник, то вихревое электрическое поле приводит в движение заряженные частицы этого проводника — так возникает индукционный ток, наблюдаемый в эксперименте.
Рис. 1. Симметричная гипотеза Максвелла (возрастание поля)
Рис. 2. Симметричная гипотеза Максвелла (убывание поля)
У электрического поля может быть два источника: электрические заряды и переменное магнитное поле. В первом случае линии электрического поля начинаются на положительных зарядах и оканчиваются на отрицательных.
Во втором случае электрическое поле является вихревым — его линии оказываются замкнутыми.
У магнитного поля также может быть два источника: электрический ток и переменное электрическое поле. При этом линии магнитного поля замкнуты в обоих случаях (оно всегда вихревое). Максвелл предположил, что оба источника магнитного поля равноправны в следующем смысле. Рассмотрим, например, процесс зарядки конденсатора (рис. 3 ):
Рис. 3. Магнитное поле внутри конденсатора совпадает с магнитным полем тока
Подчеркнём ещё раз, что симметричная гипотеза Максвелла была поначалу чисто умозрительной. На тот момент не наблюдалось каких-либо неясных физических явлений, для объяснения которых потребовалась бы такая гипотеза. Лишь впоследствии (и уже после смерти Максвелла) она получила блестящее экспериментальное подтверждение. Об этом — чуть ниже.
Прежде всего, симметричная гипотеза указала на то, что электрическое и магнитное поля тесно взаимосвязаны. Они не являются обособленными физическими объектами и всегда существуют рядом друг с другом. Если в какой-то системе отсчёта электрическое (магнитное) поле отсутствует, то в другой системе отсчёта, движущейся относительно первой, оно непременно появится.
Допустим, например, что в движущемся автомобиле покоится электрический заряд. В системе отсчёта, связанной с автомобилем, этот заряд не создаёт магнитного поля. Но относительно земли заряд движется, а любой движущийся заряд является источником магнитного поля. Поэтому наблюдатель, стоящий на земле, зафиксирует магнитное поле, создаваемое зарядом в автомобиле.
Пусть также на земле лежит магнит. Наблюдатель, стоящий на земле, регистрирует постоянное магнитное поле, создаваемое этим магнитом; коль скоро это поле не меняется со временем, никакого электрического поля в земной системе отсчёта не возникает. Но относительно автомобиля магнит движется — приближается к автомобилю или удаляется от него. В системе отсчёта автомобиля магнитное поле меняется со временем — нарастает или убывает; наблюдатель в автомобиле фиксирует вихревое электрическое поле, порождаемое переменным магнитным полем нашего магнита.
Но все инерциальные системы отсчёта абсолютно равноправны, среди них нет какой-то одной привилегированной. Законы природы выглядят одинаково в любой инерциальной системе отсчёта, и никакой физический эксперимент не может отличить одну инерциальную систему отсчёта от другой (это — принцип относительности Эйнштейна, о котором пойдёт речь в листке «Принципы СТО»). Поэтому естественно считать, что электрическое поле и магнитное поле служат двумя различными проявлениями одного физического объекта — электромагнитного поля.
Таким образом, в произвольной, наудачу выбранной системе отсчёта будут присутствовать обе компоненты электромагнитного поля — поле электрическое и поле магнитное. Но может случиться и так, что в некоторой системе отсчёта, специально приспособленной для данной задачи, одна из этих компонент обратится в нуль. Мы видели это в наших примерах с автомобилем.
Силы в правой части нам хорошо известны. Сила действует со стороны электрического поля. Она не зависит от скорости заряда.
Теория электромагнитного поля была создана Максвеллом. Он предложил свою знаменитую систему дифференциальных уравнений (уравнений Максвелла), которые позволяют найти векторы и в любой точке заданной области пространства по известным источникам — зарядам и токам (для однозначного нахождения полей необходимо знать ещё начальные условия — значения полей в начальный момент времени, а также граничные условия — некоторые условия для полей на границе рассматриваемой области). Уравнения Максвелла легли в основу электродинамики и позволили объяснить все известные на тот момент явления электричества и магнетизма. Но мало того — уравнения Максвелла дали возможность предсказывать новые явления!
Так, среди решений уравнений Максвелла обнаружились поля с неизвестными ранее свойствами — электромагнитные волны. А именно, уравнения Максвелла допускали решения в виде электромагнитного поля, которое может распространяться в пространстве, захватывая с течением времени все новые и новые области. Скорость этого распространения конечна и зависит от среды, заполняющей пространство. Но электромагнитные волны не нуждаются ни в какой среде — они могут распространяться даже сквозь пустоту. Скорость распространения электромагнитных волн в вакууме совпадает со скоростью света м/с ( сам свет также является электромагнитной волной).
Это был один из удивительных случаев в физике, когда фундаментальное открытие делалось «на кончике пера» — новое явление открывалось чисто теоретически, опережая эксперимент. Опытное подтверждение пришло позже: электромагнитные волны были впервые обнаружены в опытах Герца через восемь лет после смерти Максвелла. Эти опыты подтвердили справедливость симметричной гипотезы и основанной на ней теории электромагнитного поля, построенной Максвеллом.
Электромагнетизм для самых маленьких, и не только
Если говорить об «электромагнетизме Максвелла», то народ в целом делится на две группы: первые считают, что знают на эту тему если не всё, то вполне достаточно. Потому что ничего сложного там нет. Вторые не совсем знают эту тему и не хотят знать. Так как непонятные формулы и вообще.
Натыкаясь в разных местах на то, как объясняются некоторые моменты: с одной стороны убедительно, с другой сомнительно, с третьей неверно, с четвертой, в принципе и верно… думаю, стоит на всякий случай приглядеться им, а так как начать придется от оснований, то и «самые маленькие» могут поднянуться без боязни формул.
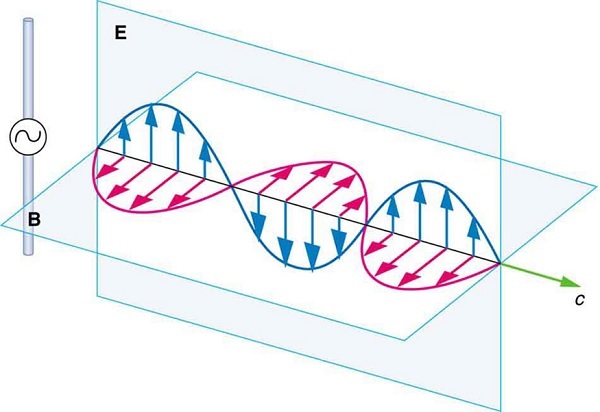
Прежде всего нас будет интересовать, как образуются и распространяются электромагнитные волны от «электрических» и «магнитных» полей, а посему сразу лакмусовая бумажка:
Если эта схема вам прекрасно знакома и не вызывает рефлекса кое-что пояснить и дополнить, чтобы не ввела других в заблуждение, то прошу под кат. Если она вам прекрасно знакома, и вы поняли, что там требуется допояснять, то гуляйте дальше) Пост не для вас.
Если схема не очень знакома или понятна, можете заглянуть.
Чтобы идти по порядку, начнем с далека, а именно — возьмем и рассмотрим окружность. Казалось бы, о чем тут говорить, фигуры проще не бывает. С детства мы привыкли рисовать, взяв точку-центр на бумаге и очертив все точки на одинаковом от центра расстоянии.
Потом мы узнаем другие способы «нарисовать» круг. Казалось бы, совсем разные принципы, а ведут к одному и тому же.
Возьмем один из них, один из полезнейших на мой взгляд:
Что это было? Ничто иное, как дифференциальное уравнение окружности. Смысл которого звучит так:
«Есть две взаимодействующие сущности. Первая прикладывает силы, чтобы усилить вторую. Вторая, по мере сил, пытается ослабить первую.»
Эту динамику мы можем записать в форме самой простой системы дифф. уравнений в мире (не считая экспоненты)
Образно говоря, в любой момент очень короткого периода одинаковой длины «dt», изменение «у» (т.е. «dy») зависит от величины «x».
При этом в этот же момент изменение «x» (т.е. «dx») зависит от величины «y».
Оба уравнения аналогичны уравнению механики макромасштабов — «расстояние = скорость * время». Только в данном случае отрезки «dt» очень малы (а точнее, бесконечно малы, но сути не меняет).
При чем все эти зависимости линейные, и об окружности им ничего не известно. А принцип инь-ян проявляется в противостоящих знаках воздействия одного элемента на другой.
Если система находится не в равновесии, т.е. «x» и «y» не равны нулю, это взаимодействие, складывая все микро-отрезки времени, приведет к бесконечному циклу колебаний.
Из этого же представления мы получаем как результат — функции синус и косинус, т.к. «х» и «у» ими соответственно и являются (с точностью до масштаба).
Отсюда же сразу понятно, почему производная синуса — косинус, косинуса — минус синус… и почему цепочка производных зацикливается. И тянется в бесконечность…
Если посмотреть на «x» и «y» (синус и косинус) на одной оси, то они конечно сдвинуты на пи/2
Итак, к чему все это.
Вернемся к электромагнитным волнам. Пустое 3-хмерное пространство. Как известно, два вида полей, электрическое и магнитное, проявляют схожую зависимость между собой.
Грубо говоря, изменение интенсивности магнитного поля порождает разницу электрического потенциала (закон Фарадея). И так же изменение электрического потенциала в точке пространства порождает магнитное поле (закон Ампера).
В уравнениях Максвелла эти зависимости между «E» (электрическое поле) и «B» (магнитное поле) выглядят так 
(еще два дополнительных уравнения сводятся к «закону сохранения энергии», и нам не будут интересны)
Прежде чем вникать в детали, следует заметить, что эта система дифф.ур. очень похожа на дифф. ур. инь-яна. Главные элементы здесь — «E», «B» и «t», на остальные параметры можно не обращать внимания, например «J» это внешнее электрическое воздействие, которое не будем рассматривать, а остальное можно принять за константы и забыть.
Кроме этого надо заметить, что и «Е», и «B», это не просто два числа, а поля трехмерных векторов в каждой точке трехмерного пространства. Но это тоже в данном случае ничего кардинально не меняет.
Зато важный элемент — треугольник с крестиком перед «Е» и «B», т.н. «ротор» поля. Из-за него как раз рождаются определенные сомнения и вопросы. К ротору вернемся чуть позже, посмотрим, что за вопросы и неясности вызывает.
Итак, мы видели, что круговая динамика это две связанные величины, которые на одном графике от времени, представляют собой две волны со сдвигом пи/2.
Таким же образом из начального возмущения распространяется электромагнитная волна, через зацикленность интенсивностей и их изменений. Изменение электрического поля порождает магнитное поле, которое, увеличиваясь (=изменяясь), порождает обратное электрическое поле, которое… и т.д. Это классическое (и верное) объяснение, известное наверное каждому.
Но… посмотрим на схему с которой все началось:
Сдвиг… где тут сдвиг? Векторы, обозначающие интенсивности полей, колеблются в одной фазе!
Ошибка? Смотрим на вики. Там то же самое. Ошибка на вики? Смотрим гугл. Что там у нас?
Какие-то непонятные споры… Должен быть сдвиг или нет? Консенсуса нет. Одни говорят «сдвиг должен быть, там везде все неправильно». Другие «доказывают», что правильно. Шок, как так? Идеальная и элегантная теория, которой 300 лет в обед, и еще какие-то неясности?
From my understanding Vern is correct. Your citation of Maxwell’s equation is a good idea, but you are incomplete. In free space you have no currents and no charges so Maxwell’s 4 equations simplify down to 2 equations (considering a single spatial dimension):
So when the temporal derivative of one is maximal the spatial derivative of the other is minimal (maximally negative). If you consider a simple single-frequency sinusoidal plane wave you find that this happens for E and B in phase. In the above equations:
E = Emax cos(kx-wt)
B = Bmax cos(kx-wt)
Вот, вышло, что должны быть в фазе. И еще в разных местах в интернете другие вариации на эту тему.
Правильно ли? Нет, неправильно.
Почему неправильно? Потому что ротор поля это не его производная по пространству!
dE/dx — так нельзя.
В других местах «упрощают» пространство до двумерного другими способами и получают тот же результат. Так тоже нельзя, ротору нужны 3 измерения (не меньше).
Посмотрим, что за это несчастный ротор. Думаю, вещь знакомая со школы.
Дело в том, что изменение электрического поля порождает не абы какое магнитное поле, а «закрученное». Типичный пример, изначальный ток по проводу, порождающий изменение электропотенциала вдоль линии провода, создает закрученное вокруг провода магнитное поле. 
То же самое с изменяющимся потенциалом магнитного поля, если изменение имеет векторную направленность, электрическое напряжение будет закручено вокруг него.
Поэтому ротор поля это не дифференциал, это специальный способ выразить его значение (наподобие смены системы координат), иначе говоря, ротор — это и есть значение поля.
Как в итоге выглядит каскадная зацикленная волна таких закрученностей?
Довольно сложно описать…
Совсем упрощенная схема выглядит так 
Но это большое упрощение, такой картинки с колечками вообще не возникает, т.к. все находится во вращении и это скорее спирали, вращающиеся вокруг друг друга. Но при этом и не спирали, т.к. расходятся в пространстве, и взаимосложение даст еще более дивную картину.
Однако в любом случае… сдвиг на пи/2 есть.
Что же насчет классического рисунка? Классический рисунок представляет собой пример однонаправленной волны линейной поляризации… Что-то похожее на лазер. Такую поляризованную волну можно получить, прибавляя к электро- волне круговой поляризации ее зеркальное отражение (стереоизомер). Получится ли после такого сложения волна с колебаниями электропотенциала и магнитной интенсивности в одной фазе?
Следует помнить, что стереоизомеры вращательно-поляризованных волн не симметричны, т.к. векторы сопуствующего магнитного поля всегда повернуты под прямым углом в одну и ту же сторону.
А поэтому… вполне возможно? Или вполне возможно нет?