что позволяет разрешить хаос
Концепции современного естествознания. Тест 2
Поможем успешно пройти тест. Знакомы с особенностями сдачи тестов онлайн в Системах дистанционного обучения (СДО) более 50 ВУЗов. При необходимости проходим систему идентификации, прокторинга, а также можем подключиться к вашему компьютеру удаленно, если ваш вуз требует видеофиксацию во время тестирования.
Закажите решение теста для вашего вуза за 470 рублей прямо сейчас. Решим в течение дня.
1. Аксиология – это
учение о материальном процессе
метрические свойства
связь различных элементов
учение о ценностях
2. Объекты, проявляющие по мере увеличения все большее число деталей – это
аттракторы
фракталы
бифуркации
нет верного ответа
3. Что исследует синергетика
эффект взаимодействия больших систем
эффект взаимодействия малых систем
линейные системы
нет верного ответа
4. Кем были заложены основы синергетики
Р. Майером, Д. Джоулем и Г. Гельмгольцем
Больцманом и Гиббсом
Г. Хакеном и И. Пригожиным
С. Карно
5. Указать неверное утверждение, что
методы синергетики в значительной степени пересекаются с методами теории колебаний и волн, термодинамики неравновесных процессов, теории катастроф, теории фазовых переходов, статистической механики и др.
синергетика исследует организационный момент, эффект взаимодействия больших систем
естественнонаучная теория не дает объяснение целой области явлений в природе с единой точки зрения
аттрактор – состояние системы, к которому она эволюционирует
6. Кем было сформулировано соотношение неопределенностей
В. В. Налимовым
В. Гейзенбергом
Ю. М. Лотман
К. Геделем
7. Что позволяет разрешить хаос
беспорядок
парадокс времени
трудности жизни
вопросы общества
8. Ключевыми моментами синергетики являются
устойчивость, универсальность
изменчивость, наследственность, отбор
нелинейность, открытость, самоорганизация
инертность, дискретность
9. Синергетический стиль мышления – это
многостороннее, нелинейное, открытое мышление
свободная игра факторов, каждый из которых взят сам по себе
познание природы на фундаментальном уровне
принцип нелинейности
10. Концепция детерминизма – это
процесс аналитического рассуждения от общего к частному
установление новых закономерностей
концепция мира, которая основывается на принципах причинности и закономерности
мысленное выделение какого-либо предмета
11. Кто выдвинул понятие диссипативной структуры
И.Р. Пригожин
Г. Хакен
В.И. Вернадский
К.Э. Циолковский
12. Синергетика в переводе с греческого означает
сочетание
сотрудничество
соединение
учение
13. Дивергенция – это
расхождение потоков энергии системы в ходе её структурных перестроек
рассеивание
сближение
приобретение в ходе эволюции сходных признаков
14. «Отбор» дарвинской триады составляют
неравновесность и иерархичность
иерархичность и гомеостатичность
гомеостатичность и нелинейность
циклическая коммуникативность и наблюдаемость
15. В чём заключается принцип подчинения
возможность моделирования эволюции системы с помощью нескольких параллельных теоретических подходов
главное в становлении не элементы, а целостная структура
возможность обобщения, усложнения структуры системы в процессе эволюции
минимальное количество ключевых параметров
Хаос — это такой порядок вещей, который мы не можем осознать
Наверное, мы все, так или иначе, попадали в ситуации, когда происходящее вокруг нас могли охарактеризовать одним лишь словом: хаос. И неважно, был ли это человек, который сеял вокруг себя, а заодно и вокруг нас, хаос, или же процесс, очень сильно напоминавший броуновское движение. Что же мы чувствовали в тот момент? Страх, растерянность, дезориентацию, потерю смысла и тревогу, а может, просто раздражение? И этот список можно продолжать. Вывод очевиден: хаос в том или ином виде, хотим мы того или нет, всегда присутствует в нашей жизни и своим присутствием приносит нам сильный дискомфорт.
Чтобы хоть как-то минимизировать дискомфортное влияние хаоса на наше психическое состояние, давайте попробуем разобраться, что же это такое.
Существует масса определений хаоса — от физико-математических до философско-эзотерических. Что может быть проще и одновременно непонятнее, чем Хаос? Хаос — это отрицание всего и вся: морали, устоев, нормальных правил общения и других общечеловеческих ценностей.
Но наиболее емкое, на мой взгляд, определение Генри Миллера: «Хаос — это такой порядок вещей, который мы не можем осознать». Неважно, в силу каких причин — не можем или не хотим.
И когда мы смотрим на проблему хаоса в нашей жизни именно с этой точки зрения, то все становиться чуть-чуть легче. Потому что мы понимаем: то, что мы называем хаосом, — это не плохо и не хорошо, это просто по-другому. Да, совсем не так, как мы привыкли, и совсем не так, как мы ожидали, и, скорее всего, совершенно не с теми результатами, которые мы прогнозировали или на которые мы рассчитывали. А это очень сильно удручает.
И что же мы делаем, когда сталкиваемся с другим порядком, тем более таким, который не можем ни понять, ни осознать? А мы, друзья мои, пугаемся. Исподволь, бессознательно, неосознанно, но очень-очень сильно. И в этот самый момент, когда мы ощущаем угрозу нашей стабильности, мы со всей яростью праведного гнева обрушиваемся на нечто, чего совсем не понимаем, но что самой своей природой непонятности несет угрозу нашему миру, нашему спокойствию, нашему порядку, такому незыблемому и надежному. Мы пытаемся загнать в прокрустово ложе «нашего порядка» или «порядка вообще» все, что выходит за рамки нашего привычного образа сознания, и смело именуем это хаосом.
Наша реакция вполне понятна: на неопределенность и неясность мы реагируем стрессами и нервными срывами. «Я ведь просто хочу ясности!» Сколько раз мы говорили эту фразу своим руководителям, своим подчиненным и коллегам, своим любимым, в конце концов? Конечно, мы же хотим ясности в отношениях, в нашем статусе, в перспективах карьерного и финансового роста, в наших должностных обязанностях… Хотим, чтобы нам все и всегда было понятно, а если что-то непонятно, то ненадолго и в небольшом количестве. Но ведь мы не можем сделать так, чтобы все в нашей жизни было разложено по полочкам, правда? Жаль, конечно, но что поделать, мы не всесильны.
Поэтому давайте подумаем: как же нам использовать тот порядок, уровень которого мы не можем осознать? Очень просто. Хаос — это огромный потенциал развития, творчество без границ и ограничений. Ведь не зря же древние греки считали хаос беспредельным, бесформенным пространством, из которого был создан существующий мир как упорядоченный космос. И греки не одиноки в своем виденье. В Китае хаос изображали в виде круга или яйца, из которого возникает все — возникает из пустоты этого круга, из окружности, точнее, даже из нефритового кольца. У жителей древнего Шумера, Вавилона и всех народов, населявших восточные горы и область между Тигром и Евфратом, хаос — это некий огромный предмет или большой диоритовый камень, который возник из черных неведомых вод, и этим водам невозможно дать определение. Даже народы доколумбовой Америки, для нас немного экзотические и малоизвестные, также упоминают хаос как исток всех вещей; во всех дошедших до нас книгах и кодексах хаос описывается как противоположность космосу, т. е. порядку, который должен возникнуть. Порядок сам по себе невозможен, потому что любой порядок рождается из хаоса и в один прекрасный момент, который случается раз либо в миллиарды лет, либо в десятилетия, в нем же и растворяется, чтобы появиться новым порядком и новыми правилами.
Упорядоченность и хаос… Две крайности, наблюдаемые нами в реальном мире. И весь вопрос не в том, что порядок лучше хаоса, потому что стабильнее, надежнее и понятнее, или что хаос лучше порядка, потому как креативнее, инновационнее и гибче, а в их соотношении друг с другом. Это как алмаз и графит. Оба они состоят из углерода, оба совершенно одинаковы, но у графита молекулы располагаются абсолютно хаотически, другими словами — не имеют ритма, и потому не пропускают свет. Благодаря этому графитом мы можем писать, рисовать, а главное — передавать малейшие нюансы света-тени и настроения. Если мы проведем графитом по бумаге, то создадим линию, а если мы проведем алмазом по бумаге, то просто ее разрежем. Потому что алмаз обладает порядком, системой, его молекулы построены так, что сквозь них проходят свет и сила, его молекулы собраны вместе очень крепко, и насколько в структуре алмаза царит порядок, настолько же в структуре графита главенствует хаос. А теперь давайте постараемся припомнить: много ли мы знаем случаев, когда из строго упорядоченного и жестко регламентированного пространства рождалось что-то принципиально новое? Или, может, некая слабоструктурированная система была надежна, долговечна и прогнозируема?
А отсюда и возникает предположение, что хаос, равно как и порядок, не больше чем инструмент развития компании в зависимости от уровня организационного развития и стратегических целей. Если ваша компания совсем молодая и только-только выходит на рынок, то уровень хаоса, неопределенности и несистематичности бизнес-процессов будет очень высок. Помимо того, что он будет высок, он будет стратегически оправдан. Потому что в любом малоструктурированном движении присутствует повышенный уровень энергии. И именно этот повышенный уровень энергии позволит достигать поставленных задач.
Если же ваша задача — удерживать долю рынка, то совершенно очевидно, что вы будете наводить порядок, структурировать организационную систему, закреплять зоны ответственности и регламентировать процедуры.
А вот если задача на определенных позициях — удержать долю рынка, а на некоторых других, менее определенных, — захватить, то, что вы будете делать, я, честно говоря, не знаю. В любом случае надо понимать, что структуризация — это не догма и не высшая добродетель, а просто инструмент. Что люди, которые во всем наводят порядок, не приведут нас к новым горизонтам. И что если мы с вами — люди творческие и нестандартные, то рядом с нами должны быть те, кто позаботится о правилах и регламентах.
Ну ладно. Это хаос «вообще», с ним все более-менее понятно. Можно смело закатывать глаза к потолку и голосом, полным трагизма и смирения, говорить: «Ну что же поделать, в этом вся дуальность мироздания». И вроде как отношения с хаосом налаживаются. А вот что делать, если, не приведи господи, руководитель грешит сильно повышенным процентным содержанием энтропии? Здесь, коллеги, самое главное — правильно самоопределиться. То есть подойти к зеркалу и, внимательно глядя в свои бездонные глаза, спросить себя: «А тебе это надо?». Иными словами, постараться понять, насколько лично нам соответствует уровень хаотичности нашего руководителя. Комфортно ли нам на таком уровне неопределенности? Если нам некомфортно, то мы просто встаем и уходим, потому что в этой ситуации никто никого не сможет изменить. А вот если мы решаем, что нас этот уровень устраивает или, что еще хуже, развитие психической мобильности лежит в зоне нашего профессионально или личностного роста, то это, конечно, тяжелый случай, но вовсе не повод сдаваться.
Так как же все-таки себя вести, что делать и о чем помнить, если твой глубокоуважаемый и любимый руководитель на твой взгляд (и только на твой. ) несколько хаотичен?
Во-первых, не надо верить пламенным заявлениям в доверительных беседах с руководителем, что он очень хочет, чтобы в его фирме был порядок. Не хочет. Что вам дадут все необходимые полномочия. Не дадут. Что надо наконец навести порядок и показать всем этим лоботрясам, где раки зимуют. Не надо, причем никому. Самое интересное, что когда он вам это говорит, то нисколько не кривит душой, так как искренне во все это верит.
Во-вторых, никогда не предлагайте стратегических планов развития, поскольку такие люди интуитивно чувствуют, что не в состоянии целенаправленно долгое время действовать для достижения какого-либо результата, и это на них действует, как красная тряпка на быка. А любые регламентирующие документы они вообще воспринимают как ограничение своих свобод и личное оскорбление.
В-третьих, все свои договоренности и разрешения фиксируйте на бумаге и закрепляйте их подписью, потому что к следующему разу он может передумать. Не со зла. Просто планы и приоритеты могут очень сильно измениться, в том числе и стратегические.
В-четвертых, когда отчитываетесь о проделанной работе, акцент делайте не на достижении результата, а на объеме выполняемых процессов.
В-пятых, наберитесь терпения, часами выжидая аудиенции в его приемной.
В-шестых, если у вас есть свои подчиненные, то всегда держите одного-двух человек посвободнее для выполнения его разовых получений;
В-седьмых, никогда не проводите сколько-нибудь важных собраний без его участия, не планируйте свою работу и никогда не испытывайте иллюзий, что вы сможете его хоть в чем-то и как-то изменить!
Ну и, наверное, самое главное. ВЕРЬТЕ В СОБСТВЕННУЮ СПОСОБНОСТЬ ВСТРЕТИТЬ ЛЮБОЙ НОВЫЙ КРИЗИС ТРИУМФОМ ТВОРЧЕСТВА!
Ирина Морозли
По материалам «Управление персоналом»
Немного о хаосе и о том, как его сотворить
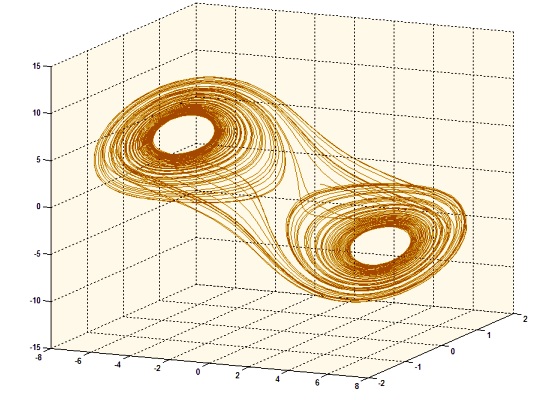
Говоря «хаос», мы, обычно, подразумеваем полное отсутствие порядка, абсолютную неупорядоченность и случайность. С математической точки зрения, хаос и порядок – понятия не взаимоисключающие. Теория хаоса (есть что-то завораживающие в названиях математических теорий) – достаточно молодая математическая область, создание которой приравнивают по значимости открытий ХХ века к созданию квантовой механики. Хаос случается в нелинейных динамических системах. Иначе говоря, любой процесс, который протекает со временем, может быть хаотичным (например, высота дерева, температура тела или популяция мадагаскарских тараканов).
Чтобы разобраться, что такое хаос, сначала обратимся к системам, такой чертой не наделённым. Детерминированные системы не допускают никаких случайностей: значение на выходе полностью определено значениями на входе. Таким образом, изменение начальных условий вызывает пропорциональное изменение результата. Так, ньютоновская механика подразумевает детерминированность, и изменяя, к примеру, силу пинка по мячу, можно ожидать соответствующее изменение в продолжительности полёта этого мяча. Так что, по принципу детерминированности, положение мяча в текущий момент полностью определено положением мяча в предыдущий момент и будущее положение зависит от текущего и всё это совсем несложно посчитать. Так, и астрономы прошлого времени полностью доверялись этому принципу и считали, что вселенная – строго детерминированная система и положение небесных тел в будущем (и в прошлом) можно рассчитать, зная их текущее положение и скорость, т.е. зная начальные условия. Предполагалось, что чем точнее известны начальные условия, тем точнее будет результат прогноза, однако известный математик Анри Пуанкаре, который (в свободное время, вероятно) занимался описанием орбит небесных тел, обнаружил, что в системах из 3-х и более тел, при незначительном изменение начальных условий (положения и скорости), траектории тела очень быстро удаляются друг от друга. Два близких набора начальных условий давали различные результаты.
Большой вклад в теорию хаоса внёс метеоролог Эдвард Лоренц. В шестидесятых годах прошлого века этот американец работал над компьютерной программой, моделирующей движение воздушных масс в атмосфере Земли. Все мы знаем, что компьютер (вопреки расхожим слухам) является строго детерминированной системой, и это создаёт известный принцип «garbage in garbage out». Лоренц гонял свою программу и в хвост, и в гриву, получая всякие разные результаты. Некоторые его коллеги даже делали предположения, что эта модель является точным предсказателем погоды, спрашивали, брать ли завтра зонтик. Разумеется, эти выводы были поспешны, вскоре выяснилась одна особенность модели погоды. Один раз для ускорения вычислений, Лоренц запустил программу не сначала, а ввёл в неё данные из предыдущего «прогона», которые были распечатаны на бумаге. Однако результаты такого запуска быстро начали отклоняться от уже полученных, формируя абсолютно другую картину. Немного неожиданно, не так ли? Оказалось, что Лоренц вводил не точные результаты прошлых вычислений, а округлённые перед выводом на печать, эта погрешность просто игнорировалась. Модель Лоренца оказалась сверхчувствительна к начальным условиям. Малейшее различие во входных данных приводило к сильному расхождению результатов с течением времени. Эта зависимость от начальных условий и была названа хаосом. Лоренцом была озвучена знаменитая черта хаоса, именуемая «эффектом бабочки», который предполагает, что в зависимости от того, махнёт ли бабочка крыльями в лесах Бразилии зависит случится ли в Техасе ураган или нет. Этот же принцип был положен в основу одноимённого фильма с Эштоном Катчером (кино ненаучное, смотреть необязательно). 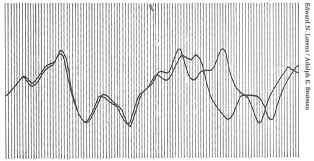
Отклонение в результатах повторных вычислений
Вся эта зависимость от начальных условий предполагает, что мы не можем делать долгосрочные прогнозы в нестабильных динамических системах. Любая погрешность в начальных условиях не позволит нам предсказать результат на какой-либо продолжительный отрезок времени. Если, к примеру, взять модель Лоренца, в качестве входных данных для определения скорости ветра нам будет необходимо ввести значения температуры и давления в каждой точке земной атмосферы, только тогда можно будет ожидать достоверный прогноз на длительный срок. Причём, входные данные должны быть абсолютно точными, т. е. с бесконечным числом знаков после запятой. А как известно, совершенно все измерительные приборы на Земле имеют ненулевую погрешность. Как бы точно не была измерена величина, всегда можно (теоретически) измерить точнее. Да и нет таких машин, которые бы позволили вводить бесконечное количество знаков после запятой. Может с приходом квантовых компьютеров что-то и изменится, не знаю.
Вот и выходит, что никуда от хаоса не деться и надо с ним мириться. Но не всё так плохо, на мой взгляд. Если бы все процессы во вселенной были бы полностью детерминированными, без единого намёка на случайность, жить было бы намного скучнее. Некоторые учёные даже склоняются к мысли о том, что хаос придаёт вселенной «стрелу времени», направленное и необратимое движение из прошлого в будущее.
Однако «хаос» и «случайность» понятия совсем не равнозначные. Определённая интерпретация процессов, кажущихся случайными, приводит их в порядок. К примеру, время между биениями сердца человека величина непостоянная, даже если человек не подвержен физ нагрузке. Если мы понаблюдаем за биением сердца некоторое время и интервалы между биениями запишем в таблицу, а также создадим второй столбец, копируя значения из первого, но со сдвигом на одно значение (т.е. первому измерению (t) в первом столбце будет соответствовать второе измерение (t+1) во втором, второму — третье и т.д;), можно будет построить карту, где по вертикали будем иметь значения без сдвига (t), а по горизонтали — значения со сдвигом(t+1). Точки на этой карте не будут рассыпаны в случайном порядке, а будут притянуты к некой области, формируя аттрактор.
Распространённый пример хаотической системы – это двойной маятник, т.е. маятник, к концу которого прикреплен второй маятник. Вы, возможно, видели подобные маятники в магазинах подарков. Так вот если взять два одинаковых маятника, поставить рядом и отклонить их приблизительно на равную величину, то уже через несколько колебаний маятники полностью рассинхронизируются. Чем точнее мы будем соблюдать начальные условия, тем дольше маятники будут качаться в такт, однако от расходимости никуда не деться. 
Такие узоры рисует лампочкой на двойном маятнике художник Джордж Иоаннидис
Долгое время теория хаоса считалась некой математической абстракцией, не имеющей подтверждения в реальных условиях. Эта проблема волновала одного японца по имени Леон Чуа, который был нацелен показать, что хаос можно создать. Для этой цели он собрал электрическую цепь.
Цепь Чуа явилась первой электрической цепью, способной генерировать хаотические сигналы. Его творение было гениально в своей простоте, цепь состояла из четырёх линейных элементов: двух конденсаторов, одной индуктивности и резистора, а также включала в себя один нелинейный локально активный элемент, на кусочно-линейной вольт-амперной характеристике которого имелась область с негативным сопротивлением. Этот элемент теперь часто называют диодом Чуа. Цепь представляет собой генератор, и диод Чуа является необходимой частью для достижения хаотических колебаний. Этот элемент недоступен как отдельный компонент, но его несложно собрать, задействовав два операционных усилителя. Другие способы реализации этой нелинейности включают в себя встречно-параллельно подключенную пару инверторов или туннельный диод (похоже, всё-таки доступен, как отдельный компонент), на ВАХ которого, как известно, имеется «долина». 
Обобщённая схема генератора Чуа и уравнения, его описывающие
Математика за всем этим стоит довольно сложная, но если не вдаваться в дебри, то эта цепь описывается тремя дифференциальными уравнениями, показывающими изменение по времени напряжения на двух конденсаторах и тока через индуктивность. Численное решение этих уравнений показывает, что при определённых соотношениях между компонентами цепи, изменение значений переменных во времени приобретает хаотический характер.
Собрать генератор Чуа труда особого не составляет. Эта цепь может демонстрировать такие явления хаоса как бифуркации и хаотический аттрактор. Однако для наблюдения всех этих чудес, будет необходим осциллограф, да ещё с двумя входами. В классическом варианте, схема состоит из двух конденсаторов, одной индуктивности, семи резисторов, микросхемы с парой операционных усилителей и двух батареек на 9В (можно использовать блок питания, но питание должно быть двухполярным). Для достижения хаотического поведения, между номиналами элементов должны соблюдаться определённые соотношения. Так, ёмкость конденсатора С2 должна быть примерно 10 ёмкостей С1, отношение С2/С1 называют α. Коэффициент β показывает отношение между R, C2 и L, а именно, β = R^2 C2 / L и должен равняться приблизительно 15. 
Принципиальная схема генератора с отрицательным сопротивлением на операционных усилителях
Итак, приступим к сборке. Собирать можно и на макетной плате, но чтобы сигналы были чётче, лучше компоненты спаять на печатной плате. В своей сборке я использовал конденсаторы на 47нФ и 470нФ, индуктивность на 15мГн и потенциометр на 1кОм (за неимением такового номиналом 2кОм, соединил его последовательно с резистором на 1кОм). Последовательно с индуктивностью можно (но необязательно) включить резистор малого номинала (до 10Ом), чтобы добавить «красоты» в сигналы. Диод Чуа реализован стандартным способом, с применением двух операционников. Я использовал микросхему TL082CP, по спецификации, это широкополосный операционный усилитель, советую использовать такой тип, с более простыми аналогами схема у меня не «завелась». Для создания характеристики с необходимыми наклонами, нам потребуются следующие номиналы резисторов: R1 = R2 = 220Ом, R3 = 2.2кОм, R4 = R5 = 22кОм, R6 = 3.3кОм. Запитать операционник можно двумя батарейками 9В, для корректной работы ОУ питание нам нужно двухполярное. Моя сборка топорная, согласен — проводки под питание и скрученные резисторы, другие мелкие недочёты, но для мониторинга хаотических сигналов этого хватило. 
Остальную часть платы сбережём для следующих проектов
После аккуратной сборки этой несложной схемы, можно попробовать посмотреть, что за сигналы она генерирует. Сигналы будем снимать с конденсаторов C1 и С2. На моей схеме я сделал два BNC разъёма для удобства подсоединения схемы к осциллографу. Подключаем кабели к осциллографу и выбираем X-Y режим, когда по одной оси у нас будет напряжение на первом конденсаторе, а по другой – напряжение на втором. Что вывести на X, а что на Y значения не имеет. Выкрутим ручку потенциометра на максимальное значение и запитаем схему. На экране осциллографа должна появиться точка. Медленно уменьшаем значение сопротивления (лучше использовать потенциометры с большим ходом и с крупной ручкой, дабы обеспечить плавность изменения сопротивления), в какой-то момент точка должна превратиться в орбиту. Последующее уменьшение сопротивления приводит к раздваиванию этой орбиты, мы начинаем наблюдать бифуркации. Удвоения периода орбиты будут происходить и дальше с уменьшением сопротивления, расстояния между последующими раздвоениями будут постоянно и планомерно уменьшаться. Т.е. разница сопротивлений между четверной и восьмерной орбитой будет меньше, чем между четверной и двойной. Скорость, с которой интервал между бифуркациями уменьшается определяется константой Фейгенбаума. Период, до которого вам удастся наблюдать бифуркации зависит от четкости сигналов (т.е. от качества соединений) и от чувствительности потенциометра (дрожание рук тоже не на пользу). В какой-то момент стабильная орбита уступает место двухпетлевому аттрактору, который знаменует наступление хаоса. Этот аттрактор имеет три точки равновесия: одну в начале координат, и две в «дырках» петель. Типичная траектория аттрактора начинает вращение вокруг одной из «дырок», удаляясь от точки равновесия с каждым витком, затем траектория либо возвращается ближе в центру и вновь удаляется, либо направляется к другой точке равновесия, где процесс повторяется. Количество вращений в каждом случае случайно.
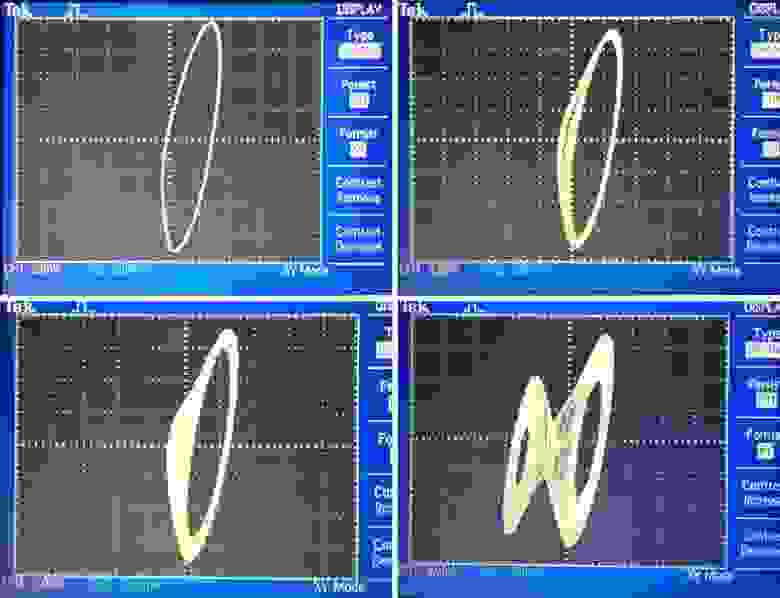
Образование хаоса через бифуркации
Этот аттрактор будет существовать в некотором интервале сопротивлений, а затем уступит место стабильной орбите, показывающей гармонические колебания. При достаточно малых значениях сопротивления, цепь превращается в простой колебательный контур, генерирующий синусоидальный сигнал с частотой, определённой значениями конденсаторов и индуктивности. Для большей «гибкости» цепи, потенциометрами можно заменить резисторы в цепи отрицательного сопротивления.
Если мы взглянем на спектр сигналов, то увидим, что в хаотическом режиме полоса генерации достаточно широкая и не имеет ярко выраженных пиков, к тому же начинается с постоянной составляющей. 
Спектр хаотического сигнала
Схема предельно проста, но её поведение изучалось многими учёными, работающими с теорией хаоса. С её помощью изучались бифуркации и создавалась целая галерея различных аттракторов. Однако кроме чисто научного интереса, данная схема имеет и практическое применение.
Поскольку это генератор, значит, его можно использовать для радиосвязи, а раз этот генератор необычный, радиосвязь можно сделать защищённой. Существует несколько типов модуляции хаотического сигнала, от простого маскирования информационного сигнала, до высокоуровневой цифровой модуляции. Высокая чувствительность хаотического генератора позволяет использовать его в качестве детектора слабых сигналов. Также сообщалось о создании генератора случайных чисел на основе данной схемы. Кроме того, как вы заметили, спектр данного генератора лежит в звуковом диапазоне, так что этой схемой не преминули воспользоваться концептуальные музыканты.
Не знаю, многие ли захотят собрать этот хаотический генератор, ибо практической пользы от него маловато, но, мне кажется, возможность поиграться с ним и понаблюдать интересные узоры на осциллографе стоит этих копеечных деталей и получаса времени. Даже если покупать все компоненты поштучно в магазине, 200 рублей – максимум, что можно потратить, но я уверен, что у многих все детали есть в загашниках!
Данная схема может быть интересна студентам математических и электротехнических факультетов. Думаю, что демонстрация работы генератора Чуа сможет заинтересовать преподавателей, в чьи научные интересы входит теория хаоса. Спасибо всем за внимание!