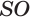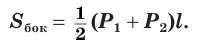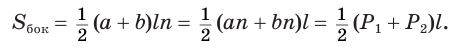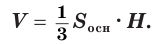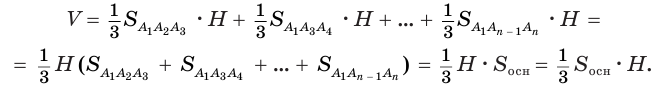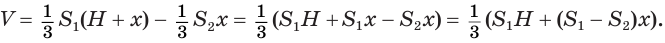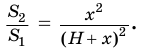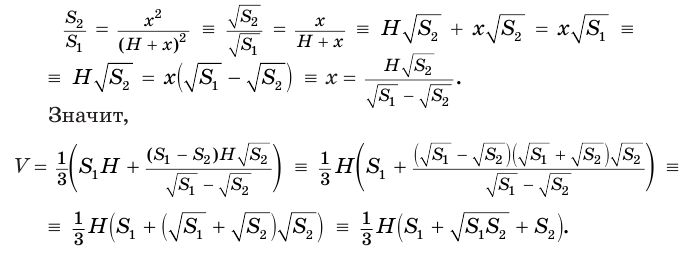что представляет собой боковая грань правильной пирамиды
Что представляет собой боковая грань правильной пирамиды
Ключевые слова: пирамида, многогранник, правильная пирамида, грань, объем, боковая поверхность
Многогранник, у которого одна грань, называемая основанием, – многоугольник,
а другие грани – треугольники с общей вершиной, называется пирамидой.
Грани, отличные от основания, называются боковыми.
Общая вершина боковых граней называется вершиной пирамиды.
Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми.
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание.
Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.
Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды.
Плоскость, параллельная основанию пирамиды, отсекает ее на подобную пирамиду и усеченную пирамиду.
Если все боковые ребра равны, то
Если боковые грани наклонены к плоскости основания под одним углом, то
См. также:
Усеченная пирамида
Описание презентации по отдельным слайдам:
Урок-практикум по решению задач Тема: ПИРАМИДЫ 10 класс
Эпиграф: «Ничто с такой силой не побуждает высокие умы к работе над обогащением знаний, как постановка трудной, но в то же время полезной задачи». Иоганн Бернулли известный математик
Решение задач 1. Найти периметр MNRK 2. Найти SABCD 3.Найти SABC 4.Найти x 5. Найти x
Теоретический тест 1.Определение пирамиды Многогранник, составленный из двухn-угольников иn-треугольников. Многогранник, составленный из двух равныхn-угольников, расположенных в параллельных плоскостях иnпараллелограммов. Многогранник, составленный из одногоn-угольника иn-треугольников. Многогранник, составленный из двух равныхn-угольников иn-треугольников. 2.Что представляет собой боковая грань пирамиды? Параллелограмм Круг Прямоугольник Треугольник 3. Определение апофемы. Высота грани пирамиды. Высота боковой грани правильной пирамиды. Высота боковой грани пирамиды. Высота грани правильной пирамиды.
Теоретический тест 4. Определение правильной пирамиды. Прямая пирамида называется правильной, если в основании лежит правильный многоугольник. Пирамида называется правильной, если в основании лежит правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Пирамида называется правильной, если отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Пирамида называется правильной, если в основании лежит многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. 5. Сколько боковых граней имеет треугольная пирамида? Одну. Две. Три. Много.
Теоретический тест 6.Площадь боковой поверхности правильной пирамиды. S=PH S=2πP S=πr S=1/2Pl 7. Площадь полной поверхности пирамиды. 2Sбок.+Sосн. 2Sбок.+2Sосн. Sбок.+Sосн. Sбок.+2Sосн. 8. Что представляет собой боковая грань правильной пирамиды? Равносторонний треугольник Квадрат Прямоугольник Равнобедренный треугольник
Теоретический тест 9. Какая фигура не может быть в основании пирамиды? Трапеция Круг. Треугольник. Квадрат. 10. Сколько оснований имеет правильная пирамида? Одно. Два. Три. Много.
Результаты теста Вопросы 1 2 3 4 5 6 7 8 9 10 1 + 2 + + 3 + + + + 4 + + +
Удивительный мир пирамид Пирамида Лувра является одним из самых оживленных мест в Париже. Многогранник имеет площадь поверхности 1000 квадратных метров, высота составляет 21,65 метра, сооружение включает в себя 95 тонн стали, 105 тонн шасси из алюминия и 673 стеклянных вставки.
Перевёрнутая пирамида находится в подземной части Лувра. Пирамида является третьим самым популярным художественным объектом среди посетителей музея после Моны Лизы и Венеры Милосской. Перевёрнутая пирамида
1.Правильная пирамида. SO – высота пирамиды. Найти площадь полной поверхности пирамиды. 2.Пирамида. SA- высота пирамиды. Найти площадь полной поверхности пирамиды Устное решение задач
Домашняя работа № 254 (в,г)
Решение задач ( дополнительные) В правильной треугольной пирамиде сторона основания 2√3, а высота равна 7 см. Найти угол наклона бокового ребра к плоскости основания. Ответ запишите в градусах. В правильной четырехугольной пирамиде сторона основания 6 см., длина бокового ребра √50 см. Найти косинус угла наклона бокового ребра к плоскости основания и площадь боковой поверхности. В правильной четырехугольной пирамиде сторона основания 4 м., а высота 2 м. Найти угол наклона боковой грани к плоскости основания и площадь полной поверхности пирамиды. Дана правильная треугольная пирамида SABC. Боковое ребро пирамиды 5 см., высота SO равна 4 см. Найти площадь полной поверхности пирамиды. Дана правильная четырехугольная пирамида SABCD с основанием ABCD. Ребро SA наклонено к плоскости основания под углом 45 º. Найти высоту пирамиды, если площадь боковой поверхности равно 18 √3. Дана правильная четырехугольная пирамида SABCD с основанием ABCD. Плоскость боковой грани наклонена к плоскости основания под углом 30º, а расстояние от точки S до прямой AD равно 2 см. Найти площадь полной поверхности пирамиды.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Перечень вопросов, рассматриваемых в теме:
Пирамида – многогранник, составленный из n-угольника и n треугольников
Основание пирамиды – грань пирамиды, являющаяся n-угольником
Вершина пирамиды – общая точка всех треугольников, лежащих в боковых гранях.
Боковая грань – грань пирамиды, являющаяся треугольником
Боковые ребра – общие отрезки боковых граней
Высота – перпендикуляр, опущенный из вершины пирамиды на ее основание
Апофема – высота боковой грани правильной пирамиды
Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, а отрезок, соединяющий вершину и центр основания пирамиды, является высотой
Усеченная пирамида – многогранник, образованный двумя n-угольниками, расположенными в параллельных плоскостях (нижнее и верхнее основание) и n-четырехугольников (боковые грани).
Площадь полной поверхности пирамиды – сумма площадей всех граней пирамиды
Площадь боковой поверхности пирамиды – сумма площадей боковых граней пирамиды
Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. и профильным изучением математики общеобразоват. Учреждений.. – М.: Дрофа, 2009. – 368 с.: ил. (117 с. – 121 с.)
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255 с. (65 с. – 68 с.)
Открытые электронные ресурсы:
Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/
Теоретический материал для самостоятельного изучения
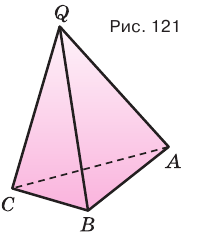
Рассмотрим многоугольник A1A2. An и точку Р, не лежащую в плоскости этого многоугольника (рис.1). Соединив точку Р с вершинами многоугольника, получим n треугольников: PA1A2, PA2A3,…, PAnA1.
Многогранник, составленный из n-угольника A1A2. An и n треугольников, называется пирамидой. Многоугольник A1A2. An называется основанием, а треугольники PA1A2, PA2A3,…, PAnA1 – боковые грани пирамиды, отрезки PA1, PA2,…, PAn – боковые ребра пирамиды, точка Р – вершина пирамиды. Пирамиду с основанием A1A2. An и вершиной Р называют n-угольной пирамидой и обозначают PA1A2. An.
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 PH является высотой. Обратите внимание, что высота может лежать и вне пирамиды (рис. 3) или быть одним из боковых ребер (рис. 4).
Рисунок 3 – высота вне пирамиды
Будем называть пирамиду правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Напомним, что центром правильного многоугольника называется центр вписанной в него (или описанной около него) окружности (рис.5).
Рисунок 5 – Правильная пирамида
Правильная пирамида обладает несколькими хорошими свойствами. Давайте выясним, какими.
Рассмотрим правильную пирамиду PA1A2. An (рис. 5).
Пусть О – центр описанной около основания окружности, тогда РО – высота пирамиды, значит РО перпендикулярен любой прямой, лежащей в плоскости основания. Таким образом, высота РО перпендикулярна радиусам А1О, А2О. АnО.
Боковые ребра пирамиды равны, значит боковые грани – равнобедренные треугольники. Основания этих треугольников равны друг другу, так как в основании лежит правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников.
Таким образом, верны следующие утверждения:
Введем еще одно определение. Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины. На рисунке 5 PE – одна из апофем.
Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.
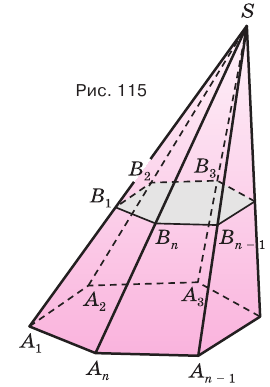
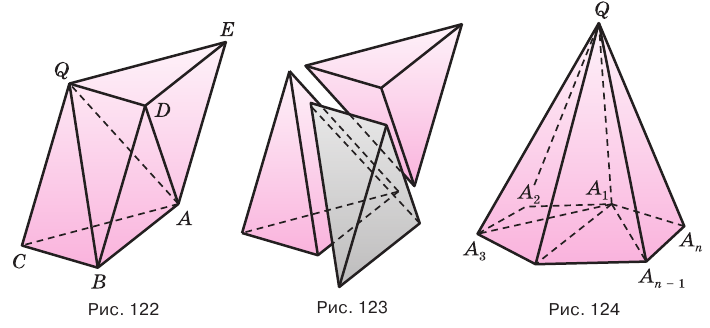
Возьмем произвольную пирамиду PA1A2. An и проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В1,В2. Вn (рис. 6). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A1A2. An и В1В2. Вn (нижнее и верхнее основания соответственно), расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2, … A1AnBnB1 (боковые грани), называется усеченной пирамидой.
Рисунок 6 – Усеченная пирамида
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды. На рисунке 7 отрезки HH1 и В1O –высоты усеченной пирамиды.
Рисунок 7 – Высота усеченной пирамиды
Площадь поверхности пирамиды
Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.
Для пирамиды, верно равенство Sполн= Sбок+Sосн.
Докажем теорему для площади боковой поверхности правильной пирамиды.
Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Для площади боковой поверхности усеченной пирамиды верна следующая теорема
Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?
Поскольку в пирамиде все боковые грани равны, то и площади их будут равны. Знаем, что площадь боковой грани на 15 меньше площади основания, значит она равна 27. В пятиугольной пирамиде боковых граней 5. Таким образом площадь полной поверхности равна 27*5+42 = 177.
Задание 2. В правильной пирамиде высота боковой грани равна 10, а в основании лежит квадрат со стороной 4. Чему равна площадь боковой поверхности?
Боковая грань пирамиды – это треугольник. Все боковые грани этой пирамиды равны между собой, так как пирамида правильная. Вычислим площадь треугольника: ½*4*10=20. В основании пирамиды лежит квадрат, значит боковых граней будет 4. Таким образом, площадь боковой поверхности равна 4* 20=80.
Пирамида
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Виды пирамид
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
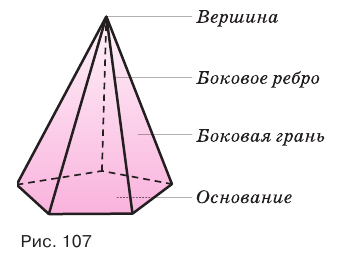
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота
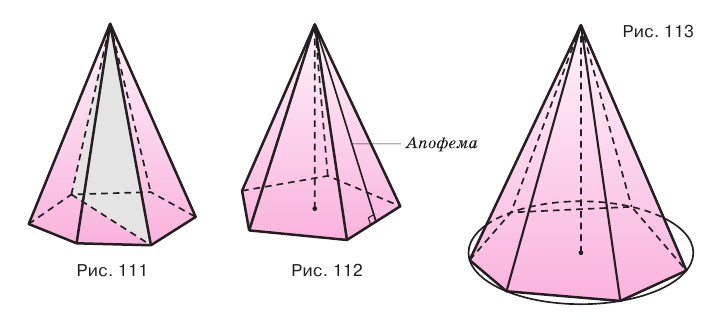
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
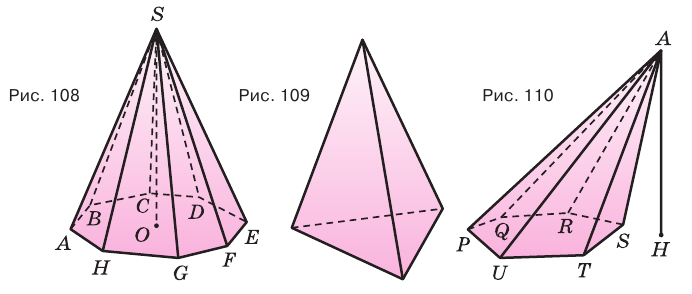
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
Отметим, что если в пирамиде равны все:
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
Если пирамиду пересечь плоскостью, параллельной основанию, то:
Используя рисунок 115, докажите эту теорему самостоятельно.
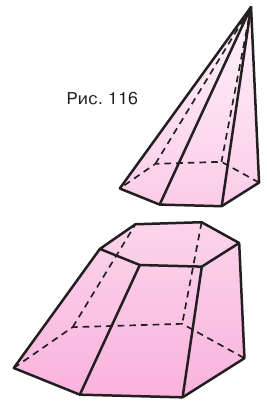
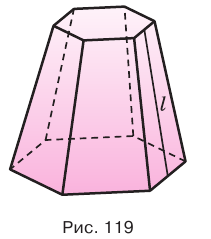
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
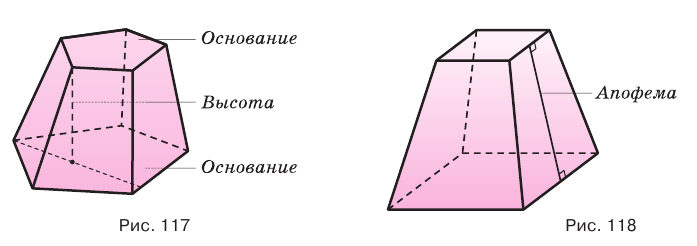
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
Доказательство:
Пусть есть правильная 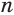
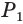
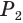
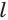
Боковая поверхность данной пирамиды состоит из 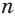
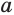
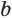
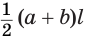
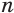
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
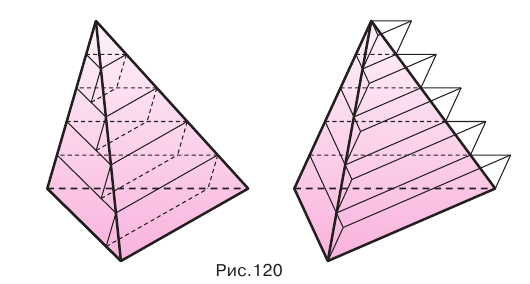
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство:
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 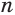
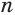
Пусть 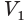
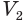


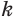
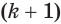


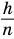
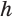
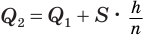
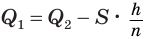
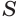
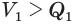
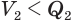
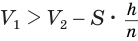
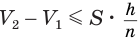
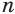
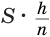
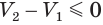
Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство
Из неравенств (1) и (2) следует, что 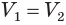
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
Доказательство:
Пусть есть треугольная пирамида 

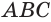
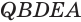
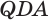


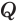
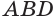
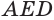




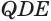

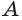
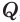





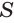

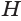



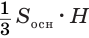
Пусть теперь есть произвольная пирамида 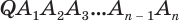
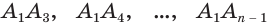
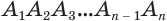
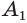
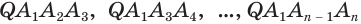

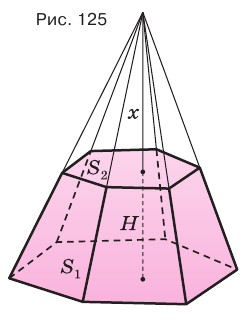
Пример:
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 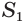
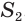

Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 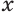
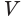
Чтобы найти высоту 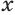
Решим это уравнение, учитывая, что 

Таким образом, объем 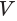


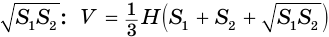
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.