что представляет собой число i

Основные действия над комплексными числами

Комплексные числа — определение и основные понятия

Обычные числа представляют собой множество действительных чисел, для обозначения которых используют букву R. Каждое число из множества можно отметить на числовой прямой.

К действительным числам носят:

Каждая точка на числовой прямой характеризуется некоторым действительным числом. Комплексное число является двумерным числом и записано в виде:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Где а и b являются действительными числами, i представляет собой так называемую мнимую единицу.

Уравнение можно мысленно поделить на несколько частей:

Следует отметить, что a + bi является единым числом, а не сложением. Места действительной и мнимой частей в уравнении можно менять:

Мнимую единицу допускается переставлять:

При таких операциях смысл выражения остается прежним. Однако стандартная запись комплексного числа имеет такой вид:

Данное утверждение можно привести в виде геометрической интерпретации. Тогда комплексные числа изображают на комплексной плоскости.

С помощью R обозначаю множество действительных чисел. В случае, когда требуется обозначить множество комплексных чисел, принято использовать букву С. Наличие буквы С на чертеже говорит о том, что на нем представлена комплексная плоскость. Данная плоскость включает две оси:

Re z — является действительной осью;

Im z — представляет собой мнимую ось.

Правила оформления такого графика практически не отличаются от требований к чертежам для декартовой системы координат. По осям задают масштаб и отмечают:

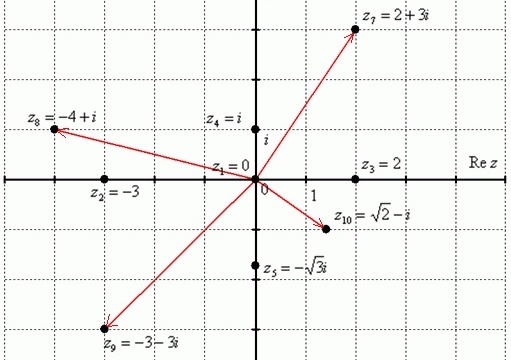
С помощью комплексной плоскости можно построить заданные комплексные числа:

Можно рассмотреть следующие комплексные числа:

Действительные числа являются частным случаем комплексных чисел. Действительная ось Re z обозначает в точности множество действительных чисел R, то есть на данной оси расположены все числа с обычными свойствами. Можно сформулировать справедливое утверждение: множество действительных чисел R представляет собой подмножество множества комплексных чисел С.

Данные числа являются комплексными числами, мнимая часть которых нулевая:

Мнимые числа с нулевой действительностью, которые расположены на мнимой оси Im z:

Есть ряд чисел с ненулевыми действительной и мнимой частью:

Для их обозначения используют точки на комплексной плоскости. К таким точкам проводят радиус-векторы из начала координат. Радиус-векторы не принято чертить к числам, которые расположены на осях и сливаются с ними.

Формы, как записываются

Алгебраическая запись комплексного числа имеет такой вид:

Кроме данной формы существует еще несколько способов для записи. Удобным и наглядным геометрическим представлением является:

z = a + bi в виде вектора с координатами (а;b) на декартовой плоскости, либо точкой — концом вектора с аналогичными координатами.

В этом случае пару комплексных чисел представляют в виде суммы соответствующих векторов, которую рассчитывают с помощью правила параллелограмма. Согласно теореме Пифагора, длина вектора с координатами (а;b) определяется, как:

Данная величина представляет собой модуль комплексного числа z = a + bi и имеет такое решение:

Вектор и положительное направление оси абсцисс образуют угол, отсчитанный против часовой стрелки. Данный угол называют аргументом комплексного числа z и обозначают, как Arg z. Аргумент имеет неоднозначное определение с точностью до прибавления величины, которая кратна 2π радиан. При повороте на такой угол вокруг начала координат вектор не изменяется.

В том случае, когда вектор длиной r с положительным направлением оси абсцисс составляет угол ϕ, его координаты будут следующими:

\(\left(r*\cos \varphi ;r*\sin \varphi \right)\)

Таким образом, получают тригонометрическую форму записи комплексного числа:

\(z=\left|z \right|*\left(\cos (Arg z)+i\sin (Arg z) \right)\)

Из-за более простого вида вкладок комплексные числа, как правило, представляют в тригонометрической форме.

Существует показательная форма для записи комплексных чисел. Какое-либо комплексное число, не равное нулю, можно представить в показательной форме:

Где \(\left|z \right|\) является модулем комплексного числа,

\(\varphi\) представляет собой аргумент комплексного числа.

Представить комплексное число в показательной форме можно с помощью нескольких действий:

Основные действия над комплексными числами с примерами

Манипуляции с комплексными числами выполняют так же, как с действительными числами. Арифметические действия могут быть следующими:

Складывать и вычитать комплексные числа можно с помощью правила:

(a + bi) ± (c + di) = (a ± c) + (b ± d)i

Умножение комплексных чисел выполняют таким образом:

(a + bi) · (c + di) = (ac – bd) + (ad + bc)i

В данном случае \(i^<2>=-1\)

Число \(\bar=a-bi\) является комплексно-сопряженным к \(z=a+bi\)

С помощью равенства \(z*\bar=a^<2>+b^<2>\) можно установить, как делить одно комплексное число на другое, не равное нулю, комплексное число:

Сложение комплексных чисел

Ели требуется сложить пару комплексных чисел:

Сначала нужно найти сумму их действительных и мнимых частей:

Таким образом, сумма какого-либо количества слагаемых определяется путем сложения действительных частей и сложением мнимых частей. В случае комплексных чисел справедливо правило первого класса, которое гласит, что от перестановки слагаемых их сумма остается прежней:

Вычитание комплексных чисел

Разность комплексных чисел:

Действие аналогично сложению. Разница заключается в необходимости выделения скобками вычитаемого числа. Далее следует раскрыть скобки и изменить знак:

Полученное в результате число обладает двумя частями. Действительная часть является составной:

Наглядно ответ будет записан в такой форме:

Умножение комплексных чисел

Можно найти произведение комплексных чисел:

Произведение будет записано таким образом:

Раскрыть скобки следует, руководствуясь правилом умножения многочленов, учитывая, что \(i^<2>=-1\)

Для того чтобы перемножить многочлены, требуется каждый член одного многочлена умножить на каждый член другого многочлена. Таким образом:

Как и в случае со сложением, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Деление комплексных чисел

На примере комплексных чисел:

требуется определить частное:

Частное будет записано в таком виде:

Делить числа необходимо с помощью метода умножения знаменателя и числителя на сопряженное знаменателю выражение. В этом случае пригодится стандартная формула:

По условию знаменатель 7-6i. В данном знаменателе уже есть (а-b), поэтому сопряженным выражением в таком случае является (a+b), то есть 7+6i. Исходя из правила, знаменатель умножают на 7+6i. Сохранить равенство можно с помощью умножения числителя на то же самое число 7+6i:

Затем в числителе необходимо раскрыть скобки, то есть умножить пару чисел, согласно отмеченному ранее правилу. Для знаменателя требуется использовать формулу \((a-b)(a+b)=a^<2>-b^<2>\) и \(i^<2>=-1\)

Уравнение будет записано в таком виде:

Нахождение аргумента

При выполнении действий с модулем комплексных чисел необходимо руководствоваться формулой:

Для поиска аргумента комплексного числа требуется использовать определенную формулу для конкретного случая. Уравнение подбирается, исходя из положения числа z = a + bi в координатной четверти. Существует всего три таких варианта:

Извлечение корня из комплексных чисел

Комплексные числа в тригонометрической форме умножают таким образом:

z_<1>*z_<2>=\left|z_ <1>\right|*\left|z_ <2>\right|*(\cos (Arg z_<1>+Arg z_<2>)+i\sin (Arg z_<1>+Arg z_<2>))2

При умножении пары комплексных чисел их модули перемножаются, а аргументы складываются. Исходя из этого утверждения, вытекают формулы Муавра:

С помощью этого равенства можно извлечь корни любой степени из комплексных чисел. Корень n-й степени из числа z представляет собой комплексное число w, которое:

Где k может обладать любым значением из множества (0, 1, …, n-1).

Таким образом, в любом случае имеется ровно n корней n-ой степени из комплексного числа. На плоскости все они будут расположены в вершинах правильного n-угольника.

Возведение комплексных чисел в степень

В качестве примера можно возвести в квадрат комплексное число:

Первый способ заключается в записи степени в виде произведения множителей:

Далее необходимо перемножить числа, согласно правилу умножения многочленов.

Второй метод заключается в использовании уравнения для сокращенного умножения:

Выражение примет следующий вид:

В случае комплексного числа можно достаточно просто записать определенную формулу для сокращенного умножения:

Такую же формулу можно представить для расчета квадрата разности, куба суммы и куба разности. Если необходимо возвести в 5-ю, 10-ю или любую другую степень комплексное число, следует воспользоваться тригонометрической формой комплексного числа, то есть формулу Муавра. К примеру, дано комплексное число в тригонометрической форме:

\(x = <-b \pm \sqrt\over 2a>z=\left|z \right|*\left(\cos \varphi +i\sin \varphi \right)\)

Данное число требуется возвести в натуральную степень n. Для этого необходимо использовать уравнение:

\(z^=\left|z \right|^*\left(\cos (n\varphi) +i\sin (n\varphi) \right)\)

Представленная формула вытекает из правила для умножения комплексных чисел, которые записаны в тригонометрической форме. Для того чтобы найти произведение чисел, требуется:

\(z_<1>=\left|z_ <1>\right|*(\cos \varphi _<1>+i\sin \varphi _<1>)\)

\(z_<2>=\left|z_ <2>\right|*(\cos \varphi _<2>+i\sin \varphi _<2>)\)

Далее требуется перемножить модули этих комплексных чисел и найти сумму аргументов:

\(x = <-b \pm \sqrt\over 2a>z_<1>* z_<2>=\left|z_ <1>\right|*\left|z_ <2>\right|*(\cos( \varphi _<1>+\varphi _<2>)+i\sin ( \varphi _<1>+\varphi _<2>)\)

Аналогичный порядок действий для показательной формы комплексного числа:

Источник

Комплексные числа

Алгебраическая форма записи комплексных чисел

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Комплексно сопряженные числа

Модуль комплексного числа

Деление комплексных чисел, записанных в алгебраической форме

Изображение комплексных чисел радиус-векторами на координатной плоскости

Аргумент комплексного числа

Тригонометрическая форма записи комплексного числа

Формула Эйлера. Экспоненциальная форма записи комплексного числа

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Извлечение корня натуральной степени из комплексного числа

Алгебраическая форма записи комплексных чисел

Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.

Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Комплексно сопряженные числа

Модуль комплексного числа

Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле

Для произвольного комплексного числа z справедливо равенство:

а для произвольных комплексных чисел z₁ и z₂ справедливы неравенства:

Деление комплексных чисел, записанных в алгебраической форме

Деление комплексного числа z₁ = x₁ + i y₁ на отличное от нуля комплексное число z₂ = x₂ + i y₂ осуществляется по формуле

Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:

Деление на нуль запрещено.

Изображение комплексных чисел радиус-векторами координатной плоскости

Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Аргумент комплексного числа

Считается, что комплексное число нуль аргумента не имеет.

Тогда оказывается справедливым равенство:

(3)

(4)

а аргумент определяется в соответствии со следующей Таблицей 1.

Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.

Таблица 1. – Формулы для определения аргумента числа z = x + i y

y z

Расположение числа z	Знаки x и y	Главное значение аргумента	Аргумент	Примеры
Положительная вещественная полуось
Положительная мнимая полуось
Второй квадрант
Отрицательная вещественная полуось	Положительная вещественная полуось
Знаки x и y
Главное значение аргумента	0
Аргумент	φ = 2kπ
Примеры

Главное
значение
аргументаАргументПримерыГлавное
значение
аргументаАргументПримерыГлавное
значение
аргументаАргументПримеры

x zТретий
квадрантЗнаки x и y

x zОтрицательная
мнимая
полуосьЗнаки x и y

y zЧетвёртый
квадрантЗнаки x и y

Положительная вещественная полуось

Главное значение аргумента:

Расположение числа z :

Главное значение аргумента:

Расположение числа z :

Положительная мнимая полуось

Главное значение аргумента:

Расположение числа z :

Главное значение аргумента:

Расположение числа z :

Отрицательная вещественная полуось

Отрицательная мнимая полуось

x z = x + i y может быть записано в виде

Формула Эйлера. Экспоненциальная форма записи комплексного числа

В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :

Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде

Из формулы (7) вытекают, в частности, следующие равенства:

а из формул (4) и (6) следует, что модуль комплексного числа

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

Действительно, умножение и деление двух произвольных комплексных чисел и записанных в экспоненциальной форме, осуществляется по формулам

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле

Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.

Извлечение корня натуральной степени из комплексного числа

Пусть — произвольное комплексное число, отличное от нуля.

Для того, чтобы решить уравнение (8), перепишем его в виде

следствием которых являются равенства

(9)

Из формул (9) вытекает, что уравнение (8) имеет n различных корней

(10)

то по формуле (10) получаем:

Источник