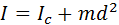что представляет собой математический маятник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

Свободные колебания. Математический маятник

При наличии механических колебаний происходит периодическое изменение кинетической и потенциальной энергии. Обращение в ноль кинетической энергии и скорости связано с максимальным отклонением тела от положения равновесия. Энергия такого колеблющегося тела достигает максимального значения. Если груз располагается на горизонтальной пружине, то потенциальная энергия считается энергией упругих деформаций пружины. У математического маятника – это энергия в поле тяготения Земли.

Гармонические колебания – это пример превращения кинетической энергии в потенциальную и наоборот.

Математический и пружинный маятник

Когда колебательная система не имеет силы трения, тогда остается неизменной полная механическая энергия.

Формулы, характеризующие груз на пружине:

Выражения при малых колебаниях математического маятника записываются:

Значение h m является максимальной высотой подъема маятника, x m и υ m = ω 0 x m – максимальными значениями отклонения физического маятника от положения равновесия и его скорости.

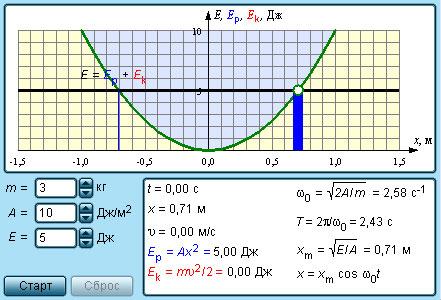
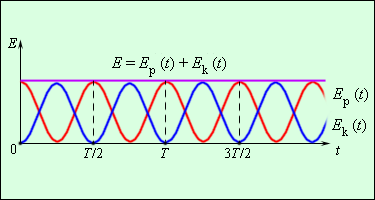
Для объяснения превращения энергии при свободных механических колебаниях без силы трения приводится иллюстрация.

Формулы кинетической и потенциальной энергии запишутся так:

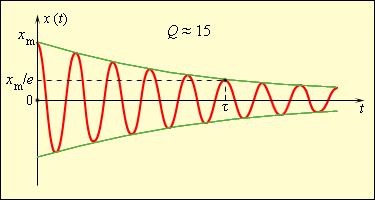
Реальные условия для колебательной системы – это наличие воздействия сил трения (сопротивления).

Скорость затухания колебаний зависит от величины сил трения.

Частота. Добротность. Формулы

Скорость затухания зависит от частоты свободных колебаний, как видно из формулы. При увеличении действия сил трения происходит уменьшение собственной частоты. Если действия силы трения достаточно велико, то изменение частоты становятся заметными.

Определение параметра представляет собой произведение числа полных колебаний N за время затухания τ на значение π :

Добротность механических колебательных систем может достигать огромных значений. Для определения Q колебательной системы применяют формулу:

То есть добротность способна характеризовать относительную убыль (затухание) энергии при наличии действия силы трения на данном промежутке времени, равняющемуся одному периоду колебаний.

Источник

Содержание:

Пружинные и математические маятники:

Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.

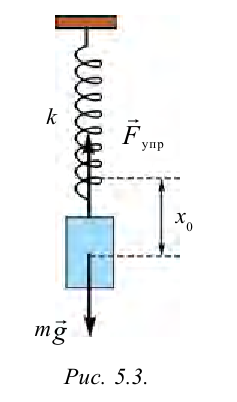
Система, состоящая из груза массой

Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:

Если учесть, что ускорение тела, совершающего гармонические колебания 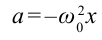, то уравнение (5.10) примет вид:

Из этого уравнения мы имеем:

Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника.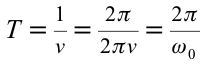

Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
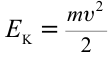
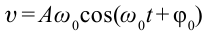
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, . В предыдущих темах было показано, что скорость можно выразить формулой . В таком случае кинетическая энергия маятника равна

Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:

В большинстве случаев важно знать полную энергию системы:

Если учесть, что ,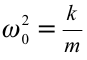

Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
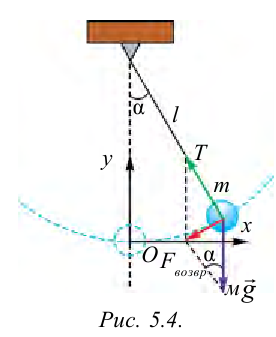
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.

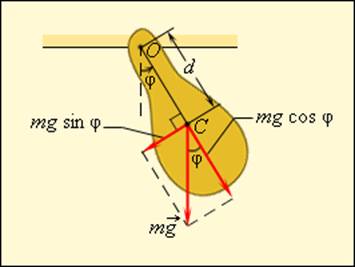
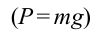
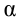
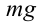
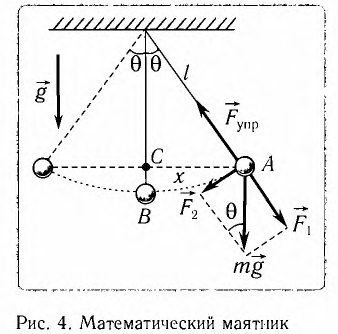
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки уравновешивает силу натяжения (рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол , силы и не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.

Из рис. 5.4. видим, что:

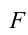
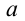
Согласно второму закону Ньютона, сила придает материальной точке ускорение , поэтому

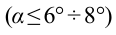
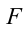
Из-за того, что угол наклона очень маленький , а сила направлена противоположно смещению, формулу (5.19) можно записать в виде

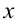
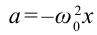
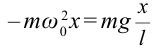
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой и учитывать соотношение , получим
Следовательно
Исходя из смысла периода колебания и учитывая, что 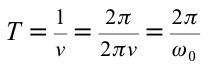получаем

Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:

Отсюда колебание математического маятника записывается следующим выражением:

Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 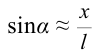и для решения уравнения движения не применяется закон синусов или косинусов.

Пример:

Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.

Решение: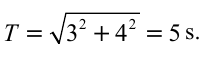

Ответ: 5 cек.

Пружинный и математический маятники

Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:

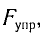
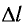
Закон Гука: модуль силы упругости , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) :

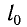
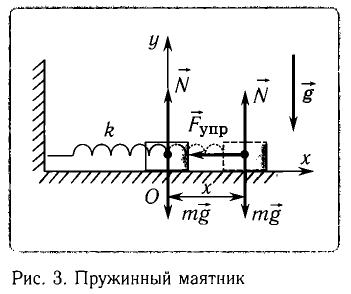
где k — жесткость тела, — длина недеформированного тела, l — длина деформированного тела.

Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.

Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).

Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 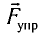направленная влево.

Запишем второй закон Ньютона для движения груза:

В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем

или

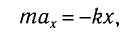
Это уравнение аналогично уравнению гармонических колебаний

Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:

Тогда период колебаний пружинного маятника можно найти по формуле

Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).

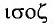
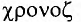
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов , — равный и — время). Таким образом, колебания пружинного маятника обладают свойством изохронности.

Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.

Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).

Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.

Галилео Галилей экспериментально определил, что период малых колебаний (9

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Свободные колебания. Математический маятник

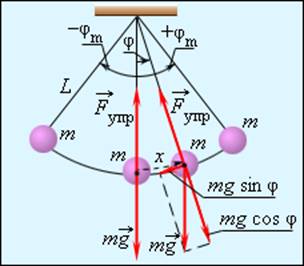
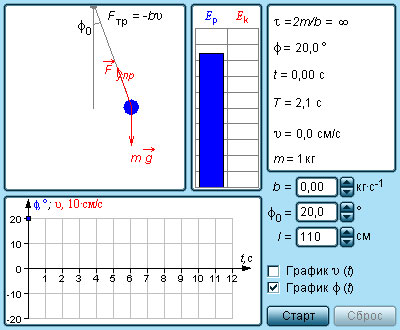
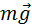
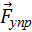
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести F_τ = –mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = lφ – смещение маятника по дуге

Если обозначить через x линейное смещение маятника от положения равновесия по дуге окружности радиуса l, то его угловое смещение будет равно φ = x / l. Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:

Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению x, а

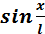
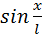
Только в случае малых колебаний, когда приближенно можно заменить на математический маятник является гармоническим осциллятором, т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15–20°; при этом величина отличается от не более чем на 2 %. Колебания маятника при больших амплитудах не являются гармоническими.

Для малых колебаний математического маятника второй закон Ньютона записывается в виде

Таким образом, тангенциальное ускорение a_τ маятника пропорционально его смещению x, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:

Эта формула выражает собственную частоту малых колебаний математического маятника.

Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:

Здесь d – расстояние между осью вращения и центром масс C.

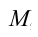
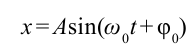
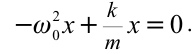
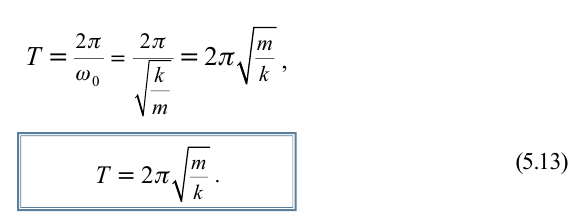
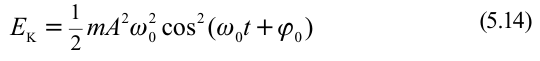
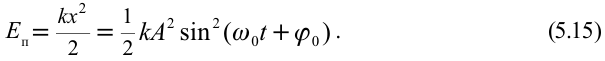
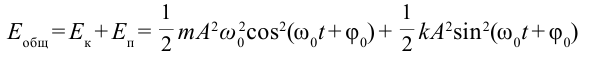
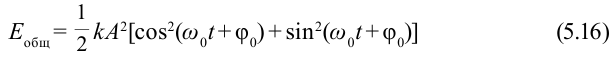
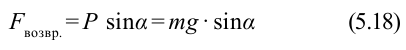
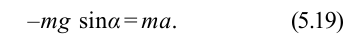
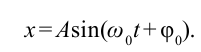
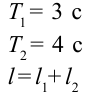
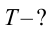
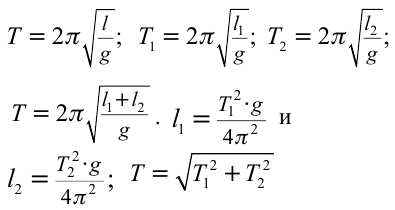
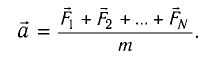
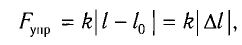
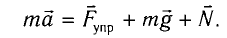
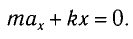
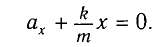
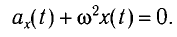
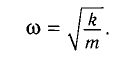
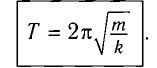
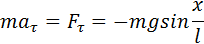
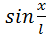
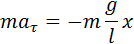
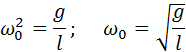
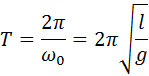
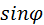Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален . Это означает, что только при малых углах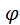, когда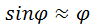, физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний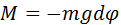

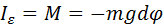
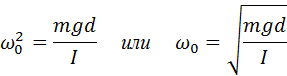
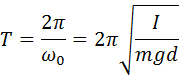
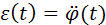
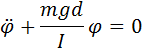
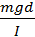и второй закон Ньютона для физического маятника принимает вид

где ε – угловое ускорение маятника, I – момент инерции маятника относительно оси вращения O. Модуль коэффициента пропорциональности между ускорением и смещением равен квадрату круговой частоты:

Здесь ω₀ – собственная частота малых колебаний физического маятника.

Более строгий вывод формул для ω₀ и T можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение ε есть вторая производная углового смещения φ по времени:

Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде

Это уравнение свободных гармонических колебаний.

Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.

По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции I можно выразить через момент инерции IC относительно оси, проходящей через центр масс C маятника и параллельной оси вращения:

Окончательно для круговой частоты ω₀ свободных колебаний физического маятника получается выражение:

Источник

• ← Уют авто черноголовка телефон
• ум это определение кратко →