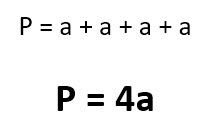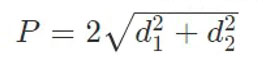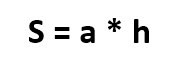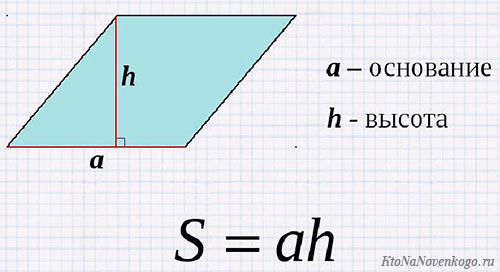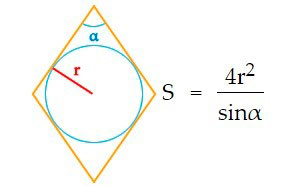что представляет собой ромб
Ромб. Формулы, признаки и свойства ромба
 |  |
| Рис.1 | Рис.2 |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
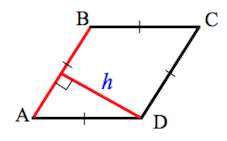
Сторона ромба
Формулы определения длины стороны ромба:
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
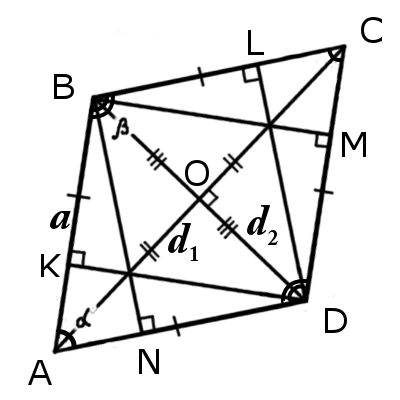
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 2 = a √ 2 + 2 · cosβ
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
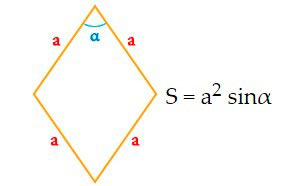
Формулы определения площади ромба:
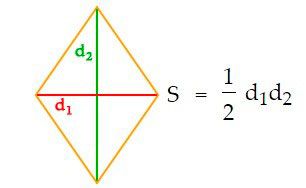
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
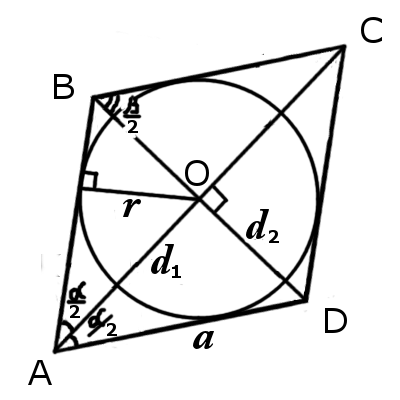
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
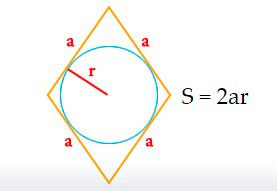
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Ромб – между параллелограммом и квадратом
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем о такой геометрической фигуре, как РОМБ. Многие наверняка знают, как он выглядит.
Особенно спортивные болельщики, так как эмблемы многих команд связаны именно с ромбом. Тут достаточно вспомнить одну из главных российских команд – Спартак. Вот так она выглядит.
Ромб — это.
А вот как звучит официальное определение ромба:
История возникновения самого слова весьма примечательна. На древнегреческом оно звучит как «ῥόμβος», а на латыни «rombus». И переводятся оба слова как «бубен».
Дело в том, что в Древней Греции делали барабаны и прочие ударные инструменты чаще именно такой формы. Просто натягивать ткань на параллелограмм было гораздо проще. А вот круглые, более привычные нам сегодня барабаны появились позже.
И еще один интересный факт – карточная масть «бубны» называется так точно по той же причине.
Говоря об определении РОМБА, не лишним будет тогда сказать и что такое параллелограмм, раз он там фигурирует.
Параллелограмм – это геометрическая фигура, которая представляет собой четырехугольник, у которого противоположные стороны равны между собой и параллельны друг другу.
Выглядит классический параллелограмм вот так:
Впервые его описал знаменитый древнегреческий математик Евклид в своей книге «Начала». Это произведение вышло в 300 году до нашей эры. И было посвящено основам математики, которые были известны на то время.
В частности, Евклид в своей книге разделил все четырехугольники на две большие категории – параллелограмм и трапеция (так как у нее две стороны не параллельны друг другу). Также в «Началах» Евклид указал, что ромб является частным случаем параллелограмма, так как у него противоположные стороны равны.
И наконец, частным случаем самого ромба является квадрат. У него противоположные стороны не только равны, но еще и пересекаются под прямым углом.
Признаки ромба
Чтобы понять, что перед нами ромб, должно выполняться всего лишь одно из трех простых условий:
И тут будет не лишним подтянуть теоретическую базу и напомнить, что такое диагональ, и уж тем более что такое биссектриса.
Диагональ – это отрезок, который соединяет две любые вершины в многоугольнике, которые не находятся рядом друг с другом.
Если говорить конкретно о четырехугольнике, которым является и ромб, то диагональ соединяет две противоположные вершины и никак иначе. И таких диагоналей в ромбе две:
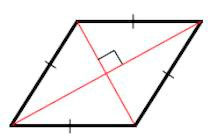
На этом рисунке диагоналями являются отрезки AC и BD. И как показано, они пересекаются под прямым углом, о чем и говорится во втором признаке ромба.
Биссектриса – это линия, которая выходит из угла и делит его ровно на две части.
Кстати, само слово «биссектриса» имеет латинские корни. Оно состоит из двух половин – «bi» (двойное) и sectio (разрезание).
Свойства ромба
А можно все и перевернуть таким образом. Если вы точно определи, что перед вами ромб, то тогда для этой фигуры будут характерны вот такие свойства:
И есть еще одно свойство, которое помогает решать различные задачки на уроках геометрии. Оно звучит так:
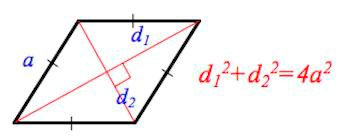
Сумма квадратов обеих диагоналей ромба равна квадрату его сторону, умноженному на четыре.
Периметр ромба
Чтобы определить периметр любого четырехугольника, надо просто сложить между собой длины всех его сторон.
В случае с ромбом это совсем просто, так как они все равны между собой. И тогда формула для вычисления периметра получается такой:
Как несложно догадаться, буква «а» здесь – это длина стороны ромба.
Есть еще одна формула для вычисления периметра ромба – через диагонали. Она более сложная, но при решении различных задач вполне может и пригодиться.
Площадь ромба
Площадь любой геометрической фигуры – это размер пространства, заключенного в границы этой самой фигуры.
Классическая формула для расчета площади ромба – через длины стороны и высоты.
Главное, надо напомнить, что такое высота. Это отрезок, проведенный из вершины геометрической фигуры под прямым углом к противоположной стороне.
Она обозначается буквой «h» или «H» и выглядит вот так:
И наконец, формула для расчета площади ромба через сторону и высоту:
Есть и другие формулы для расчета площади ромба:
Вот и все, что мы хотели рассказать о ромбе.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Со временем, разница между квадратом, ромбом и параллелограммом забывается. То, что было само собой разумеющимся в школе, теперь кажется чем-то новым!:) Кстати, во времена СССР, именно ромб был самой популярной фигурой в дизайне всевозможных логотипов.
Что такое ромб: определение, свойства, признаки
В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.
Определение ромба
Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).
Примечание: квадрат является частным случаем ромба.
Свойства ромба
Свойство 1
Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.
Свойство 2
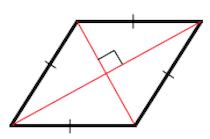
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.
Свойство 3
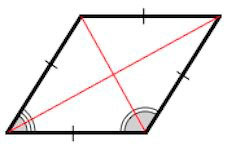
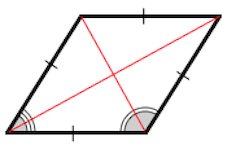
Диагонали ромба являются биссектрисами его углов.
Свойство 4
Сторону ромба a можно найти через его диагонали d1 и d2 (согласно теореме Пифагора).
Свойство 5
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Радиус вписанной в ромб окружности r вычисляется по формуле:
Признаки ромба
Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:
Примечание: Любой четырехугольник, стороны которого равны, является ромбом.
Ромб. Свойства и признаки ромба
Ромб – это параллелограмм, у которого все стороны равны.
Если у ромба – прямые углы, то он называется квадратом.
Свойства ромба
1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
Помимо этого:
2. Диагонали ромба перпендикулярны.
3. Диагонали ромба являются биссектрисами его углов.
4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Признаки ромба
Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:
1. Все стороны параллелограмма равны между собой ().
2. Диагонали пересекаются под прямым углом ().
3. Диагонали параллелограмма являются биссектрисами его углов.
Площадь ромба
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
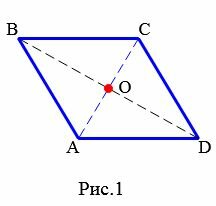
Что представляет собой ромб
Определение 1. Ромб − это параллелограмм, у которого все стороны равны.
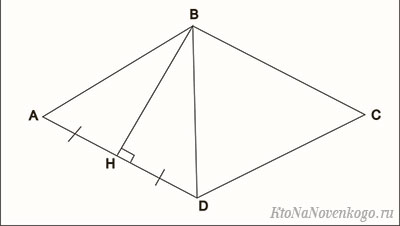
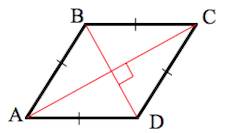
На рисунке 1 изображен ромб ABCD.
 |
Определение 2. Ромб − это четырехугольник, у которого все стороны равны.
Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.
Объединение ромба и ограниченной им части плоскости также называют ромбом.
Свойства ромба
Поскольку ромб является параллелограммом, то имеет следующие свойства:
Ромб имеет также и следующие свойства:
Докажем свойства 6 и 7, сформулировав следующую теорему:
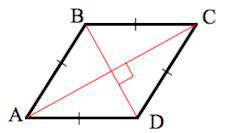
Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.
Доказательство. По определению 1, \( \small AD = DC \) (Рис.2). Следовательно треугольник \( \small DAC \) равнобедренный. Тогда \( \small \angle DCO = \angle DAO. \) Учитывая, что \( \small AO = OC \) (свойство 5 ромба), получим, что треугольники \( \small DOA \) и \( \small DOC \) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно \( \small \angle DOC= \angle DOA=90°. \) То есть диагонали AC и BD перпендикулярны.
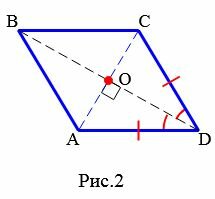 |
Из равенства треугольников \( \small DOA \) и \( \small DOC \) также следует, что \( \small \angle CDO= \angle ADO,\) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.
Признаки ромба
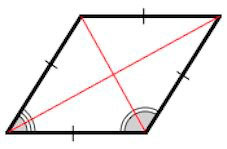
Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.
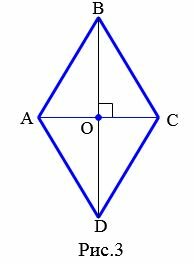 |
Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.
Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.
Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.
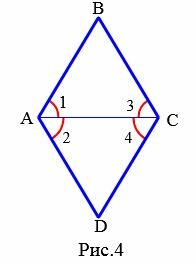
Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.
 |
Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.
Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.