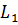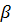что представляет собой сечение цилиндра плоскостью параллельной его оси

Что представляет собой сечение цилиндра плоскостью параллельной его оси

· рассмотреть основные виды сечений цилиндра

Время реализации занятия: 45 минут

I Организационный момент

II Проверка домашнего задания

III Изучение нового материала

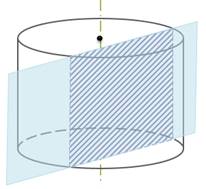
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 1, а). Две его стороны — образующие цилиндра, а две другие — параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это — сечение цилиндра плоскостью, проходящей через его ось (рис. 1, б).

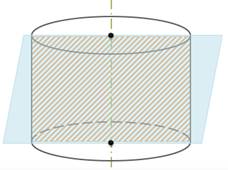
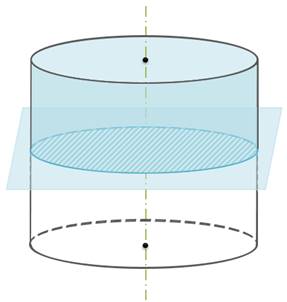
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Пусть β — плоскость, параллельная плоскости основания цилиндра (рис. 2). Параллельный перенос в направлении оси цилиндра, совмещающий плоскость Р с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью Р с окружностью основания. Теорема доказана.

IV Закрепление изученного материала

Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра.

Источник

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Основные элементы цилиндра

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Источник

Опорный конспект по геометрии на тему «Цилиндр»

Опр. Цилиндром называется тело, которое состоит из двух кругов, совмещаемых

параллельным переносом и всех отрезков, соединяющих соответствующие точки

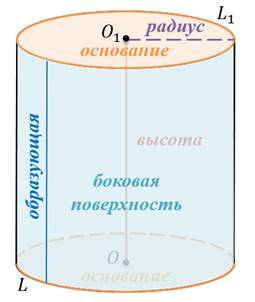
Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей этих кругов – образующими цилиндра (рис. 1)

рис. 1 рис. 2 рис. 3 рис. 4

1) Основания цилиндра равны и лежат в параллельных плоскостях.

2) Образующие цилиндра равны и параллельны.

Опр. Радиусом цилиндра называется радиус его основания.

Опр. Высотой цилиндра называется расстояние между плоскостями его оснований.

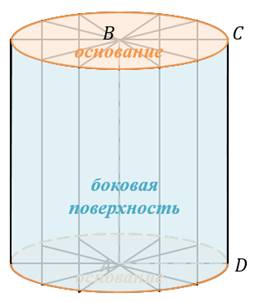
Опр. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Осевое сечение цилиндра – прямоугольник со сторонами 2 R и l (в прямом цилиндре l = Н) рис. 2

Сечение цилиндра, параллельные его оси, являются прямоугольниками (рис. 3).

Сечение цилиндра плоскостью, параллельной основаниям – круг, равный основаниям (рис. 4)

Площадь поверхности цилиндра.

Боковая поверхность цилиндра составлена из образующих.

Полная поверхность цилиндра состоит из оснований и боковой поверхности.

S _полн = 2 S _осн + S _бок; S _осн = П ∙ R 2 ; S _бок = 2 П ∙ R ∙Н S _полн = 2П R ∙( R + Н)

№1. Радиус цилиндра равен 3см, а его высота- 5см. Найдите площадь осевого сечения и площадь пол-

ной поверхности цилиндра.

№2. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом и равна 20 см. Найдите площадь боковой поверхности цилиндра.

№3. Радиус цилиндра равен 2см, а его высота- 3см. Найдите диагональ осевого сечения цилиндра.

№4. Диагональ осевого сечения цилиндра, равная , образует с плоскостью основания угол . Найдите площадь боковой поверхности цилиндра.

№5. Площадь боковой поверхности цилиндра равна 15. Найдите площадь осевого сечения.

№6. Найдите высоту цилиндра, если площадь его основания равна 1, а S _бок = .

№7. Диагональ осевого сечения цилиндра имеет длину 8см и наклонена к плоскости основания под углом . Найдите полную поверхность цилиндра.

Цилиндрическая дымовая труба с диаметром 65см имеет высоту 18м. Сколько жести нужно для её изготовления, если на заклепку уходит 10% материала?

Источник

Понятие цилиндра

Урок 12. Геометрия 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Понятие цилиндра»

На этом уроке мы вспомним понятие цилиндра. Дадим его определение. Рассмотрим, какими элементами обладает цилиндр.

Вокруг нас существует множество объектов, которые являются физическими моделями цилиндра, или проще говоря, имеют форму цилиндра.

Например, кружки и стаканы имеют форму цилиндра. Карандаши, шляпы, пуфики, барабан также имеют форму цилиндра.

Некоторые архитектурные сооружения.

Колонны храмов и соборов, выполненные в форме цилиндра, подчеркивают их гармонию и красоту.

Итак, перейдём к самому цилиндру. Рассмотрим произвольную плоскость и окружность с центром О радиуса , лежащую в этой плоскости. Через каждую точку окружности проведем прямую, перпендикулярную к плоскости .

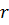
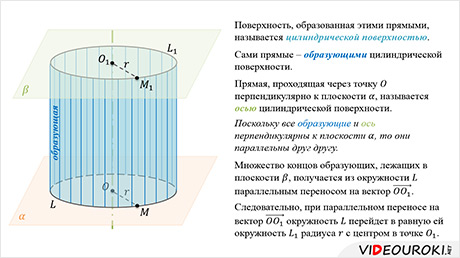
Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые – образующими цилиндрической поверхности.

Прямая, проходящая через точку О перпендикулярно к плоскости , называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости , то они параллельны друг другу.

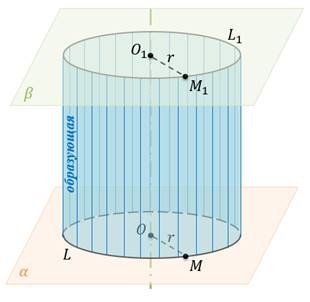
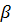
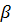
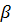
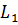
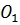
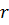
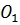
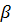
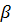
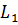
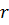
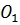
Рассмотрим теперь плоскость , параллельную плоскости . Отрезки образующих, заключённые между плоскостями и , параллельны и равны друг другу. По построению концы этих отрезков, расположенные в плоскости , заполняют окружность . Концы же, расположенные в плоскости , заполняют окружность с центром радиуса , где – точка пересечения плоскости с осью цилиндрической поверхности. Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости , получается из окружности параллельным переносом на вектор . Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор . окружность перейдёт в равную ей окружность радиуса с центром в точке .

Тело, ограниченное цилиндрической поверхностью и двумя равными кругами с границами и , называется цилиндром.

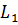
Можно ещё услышать и такое определение: прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями и , которые перпендикулярны образующим цилиндрической поверхности.

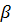
Назовём элементы цилиндра.

Круги называются основаниями цилиндра.

А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.

Ось цилиндрической поверхности называется осью цилиндра.

Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между основаниями цилиндра.

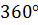
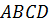
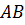
Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон на . Итак, если взять некоторый прямоугольник и вращать его вокруг одной из сторон, например, вокруг стороны , то в результате получим тело, которое и называется цилиндром.

В этом случае основания цилиндра образуются вращением сторон 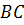и , а боковая поверхность цилиндра образуется вращении стороны .

Теперь рассмотрим сечения цилиндра различными плоскостями.

Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.

Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось.

Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие цилиндра, а две другие – хорды оснований цилиндра.

Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.

В самом деле, такая секущая плоскость отсекает от данного цилиндра тело, которое также является цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.

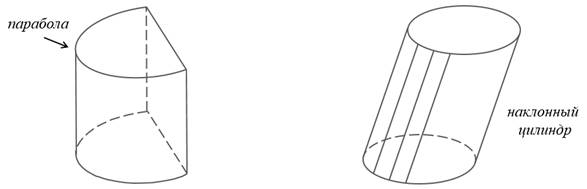
Замечание. На практике очень часто встречаются предметы, которые имеют форму сложных цилиндров.

На экране, на первом рисунке вы видите цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком. На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований, такой цилиндр называют еще наклонным цилиндром. Однако в дальнейшем мы будем рассматривать только прямые круговые цилиндры.

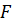
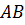
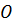
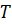
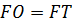
Задача: точка – середина образующей цилиндра, центрами оснований которого являются точки и . Верно ли, что ?

Решение: рассмотрим и .

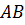
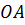
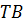
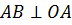
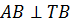
Образующая перпендикулярна плоскостям, в которых лежат основания цилиндра. Следовательно, она перпендикулярна любой прямой лежащей в этих плоскостях. Прямые и являются радиусами цилиндра и лежат в плоскостях оснований. Значит, прямая и . Отсюда получаем, что и – прямоугольные.

Так как основаниями цилиндра являются равные круги, то 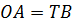, как радиусы.

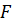
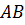
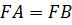
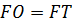
Так как по условию задачи точка – середина образующей цилиндра, то отрезки . Значит, равны по двум катетам. Отсюда вытекает, что .

Ответ: .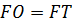

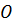
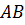
Задача: точка – центр основания цилиндра. Отрезок – диаметр другого его основания. Вычислите площадь , если радиус цилиндра равен см, а его высота – см.

Решение: напомним, что площадь треугольника находится по формуле . Заметим, что высота цилиндра является и высотой нашего и равна . А основание треугольника есть диаметр цилиндра и равно оно двум радиусам, т.е. (см).

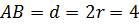
Подставим в формулу площади треугольника высоту и длину основания треугольника. Посчитаем. Получим, что площадь треугольника равна 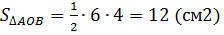. Не забудем записать ответ.

Задача: радиус цилиндра 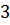см, а его высота – см. Вычислите площадь осевого сечения.

Решение: напомним, что осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Высота цилиндра – это есть длина образующей 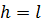. Следовательно, ширина осевого сечения равна . Длина сечения равна диаметру основания цилиндра. И значит, равна (см).

Теперь вычислим площадь осевого сечения. Она равна ().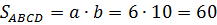

На этом уроке мы вспомнили понятие цилиндра. Узнали, что тело, ограниченное цилиндрической поверхностью и двумя кругами с границами и , называется цилиндром. Или прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями и , которые перпендикулярны образующим цилиндрической поверхности. Назвали элементы цилиндра. А также рассмотрели сечения цилиндра различными плоскостями.

Источник