что приводит под одну амплитуду принимаемые сигналы
1.3 Сигналы
1.3.1 Синусоидальные сигналы
Рис. 1.19 Синусоидальный сигнал с амплитудой A и частотой f
Ещё одним вариантом описания является выражение для угловой частоты \[ V=A\sin (ω t ). \]
Обычно приходится иметь дело с синусоидальными сигналами из диапазона от нескольких герц до нескольких десятков мегагерц. Низкие частоты вплоть до 0.0001 Hz можно получить, если аккуратно собрать нужную схему. Частоты до 2000 MHz ( 2 GHz) требуют использования согласованных линий передачи. На более высоких частотах обычные электронные схемы перестают работать, и требуются специальные приёмы проектирования.
1.3.2 Амплитуда и децибелы
1.3.2.A Децибелы
Исходно децибелы использовались для указания отношения двух сигналов, но иногда подразумевается некоторый опорный источник, и амплитуда указывается относительно него. Существует несколько стандартных уровней ( которые не стандартизованы, но вполне очевидны ), используемых подобным образом. Вот список популярных вариантов.
Помимо перечисленных, есть и иные стандартные уровни, используемые в других областях инженерного дела и науки.
1.3.3 Прочие сигналы
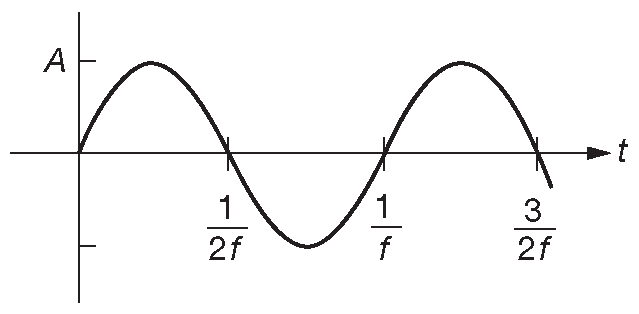
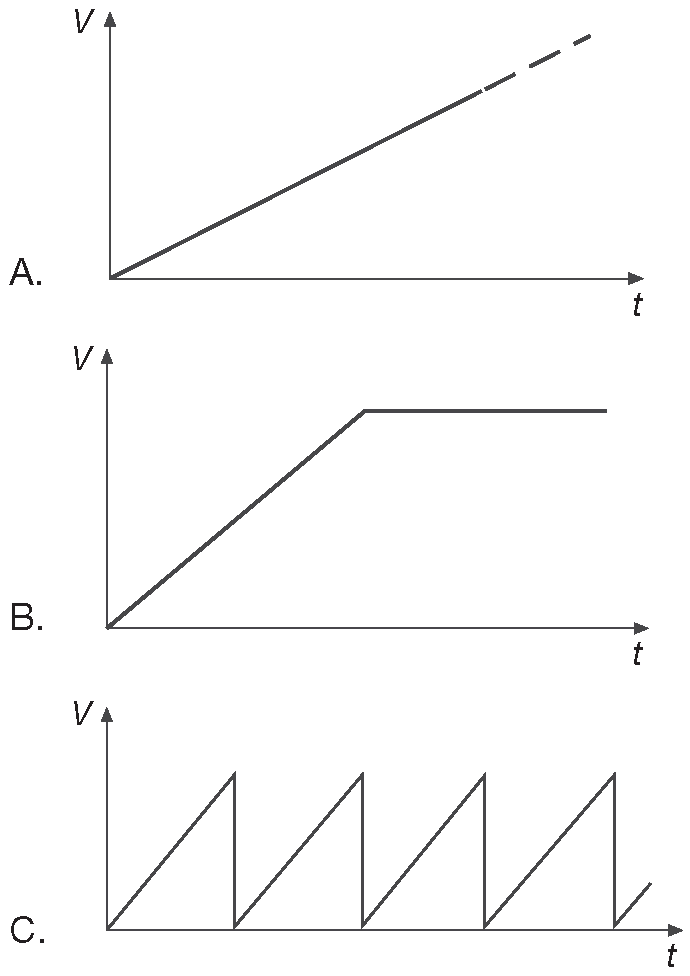
1.3.3.A Линейно меняющийся
Рис. 1.20 (A) Линейно меняющийся сигнал. (B) Линейно меняющийся сигнал с ограничением. (C) Пилообразный сигнал
Измерение амплитуды сигналов
Амплитуду синусоидального сигнала, а также любого другого сигнала, можно оценивать не только как абсолютное максимальное его значение. Иногда пользуются понятием двойная амплитуда (амплитуда от пика до пика сигнала), которая, как нетрудно догадаться, равна удвоенной амплитуде. Иногда употребляют понятие эффективное значение, которое определяется следующим образом: UЭФФ = 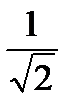
Измерение амплитуды в децибелах. Как сравнить амплитуды двух сигналов? Можно, например, сказать, что сигнал X в два раза больше, чем сигнал Y. Во многих случаях именно так и производят сравнение. Но очень часто подобные отношения достигают миллионов, и тогда удобнее пользоваться логарифмической зависимостью и измерять отношение в децибелах (децибел составляет одну десятую часть бела, но единицей «бел» никогда не пользуются). По определению отношение двух сигналов, выраженное в децибелах:
Хотя децибел служит для определения отношения двух сигналов, иногда эту единицу используют для измерения абсолютного, а не относительного значения амплитуды. Дело в том, что можно взять некоторую эталонную амплитуду и определять любую другую амплитуду в децибелах по отношению к эталонной. Известно несколько стандартных значений амплитуды, используемых для такого сравнения (эти значения не указываются, но подразумеваются); приведем некоторые из них: а) дБВ – эффективное значение 1 В; б) дБВт – напряжение, соответствую-щее мощности 1 мВт на некоторой предполагаемой нагрузке, для радиочастот это обычно 50 Ом, для звуковых частот – 600 Ом (напряжение 0 дБВт на этих нагрузках имеет эффективное значение 0,22 В и 0,78 В); в) дБп – небольшой шумовой сигнал, генерируемый резистором при комнатной температуре. Нужно обратить внимание на эталонную амплитуду 0 дБ: при использовании этого значения нужно не забывать его оговаривать, например «амплитуда 27 дБ относительно эффективного значения 1 В», или в сокращенной форме «27 дБ относительно 1 Вэфф» или пользоваться условным обозначением дБВ.
Импульсные сигналы
Электрическим импульсом называют напряжение или ток, отличающийся от нуля и имеющий постоянное значение лишь в течение короткого промежутка времени, меньшего или сравнимого с длительностью установления процессов в электрической системе, в которой действует этот ток или напряжение. В случае следующих друг за другом импульсов обычно предполагается, что интервал между ними существенно превышает длительность процессов установления.
В противном случае этот сигнал называют переменным напряжением или током сложной формы. С чисто математической точки зрения переходные процессы протекают, как известно, бесконечно долго, поэтому данное определение не совсем строго. Однако в реальных цепях длительность этих процессов не превышает 3τ, где τ – постоянная времени цепи, поэтому такое определение вполне допустимо.
Все многообразие электрических импульсов можно разделить на видеоимпульсы (рис. 1.2, а) и радиоимпульсы (рис. 1.2, б).
Связь между этими двумя типами импульсов состоит в том, что огибающая радиоимпульса представляет собой видеоимпульс. Частота синусоидального сигнала, которым заполнен видеоимпульс, называется частотой заполнения. Системы автоматики и управления оперируют в основном с видеоимпульсами, которые в дальнейшем будем называть просто импульсами.
Рис.1.2. Видео- и радиоимпульсы
На рис.1.3 приведен пример реального импульса.
Основными характеристиками и параметрами импульсов являются:
1.Амплитуда импульса Um = А;
2.Активная длительность импульса (измеряется на уровне 0,1А) tИ;
Рис. 1.3. Реальный прямоугольный импульс
5.Искажение вершины импульса ΔU;
6.Амплитуда обратного выброса Um ОБР;
7.Длительность обратного выброса tИ ОБР;
8.Мощность импульса P = W/tИ, где W – энергия импульса.
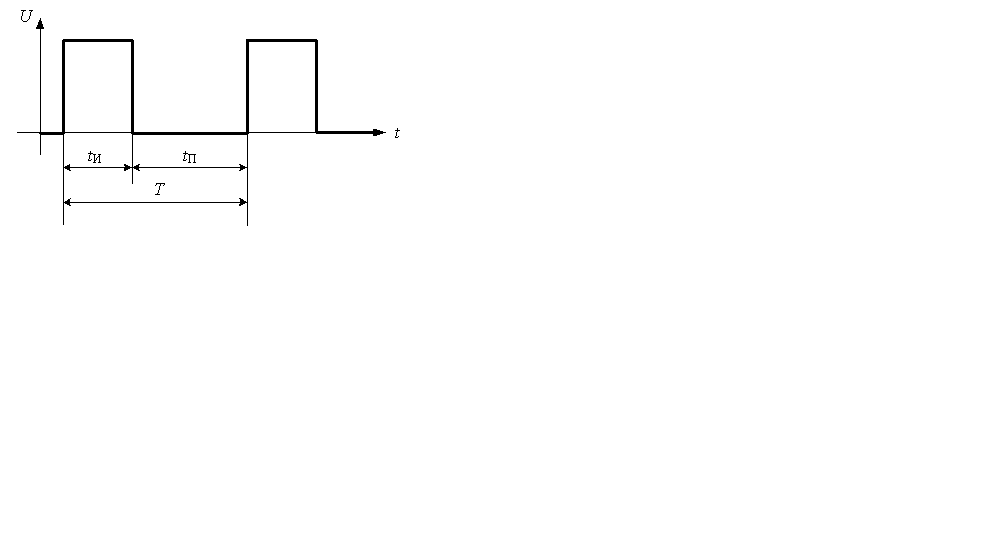
Периодически повторяющиеся импульсы образуют импульсную последовательность (рис.1.4). Она характеризуется следующими параметрами:
1.Частота импульсной последовательности ƒ = 1/Т, где T = tИ + tП;
2.Коэффициент заполнения γ = tИ/Т (диапазон изменения 0…1) и скважность Q = Т/tИ (диапазон изменения от 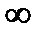
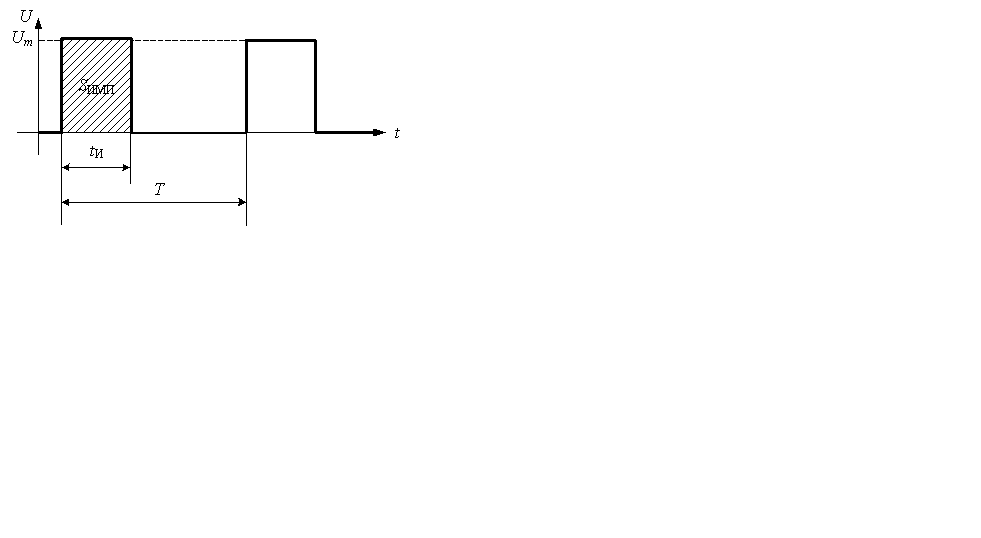
3.Среднее значение импульса (рис.1.5)
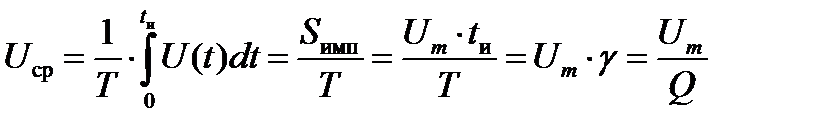
Рис. 1.4. Импульсная последовательность
Рис. 1.5. Определение среднего значения импульса
Импульсы имеют различную форму: прямоугольные, треугольные, трапецеидальные, экспоненциальные и др. (рис.1.6), так же могут быть однополярными (а) и разнополярными (б) (рис.1.7). Однополярные импульсы могут быть положительными и отрицательными. Для получения импульсных последовательностей различной формы, частоты и амплитуды применяют специальные генераторы.
Рис. 1.6. Треугольные (а), трапецеидальные (б), экспоненциальные (в) импульсы
Рис. 1.7. Однополярные положительные (а) и разнополярные (б) прямоугольные импульсы
При анализе работы систем автоматического управления и их отдельных элементов в качестве типовых возмущений используют одно из следующих.
Ступенчатое возмущение — мгновенное изменение воздействия на постоянную величину, чаще всего равную единице измерения (рис. 1.8, а). Физически система испытывает толчок. Аналитически
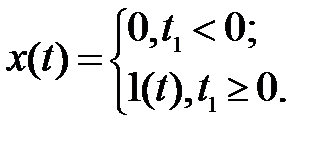
Единичный скачок в момент t1 пo отношению к моменту t0 аналитически записывается в виде 1( t1 – t0).
Рис.1.8. Типовые возмущения
2. Импульсное возмущение – это возмущение, полученное как последовательность двух одинаковых по величине, но противоположных по знаку ступенчатых возмущений, сдвинутых во времени. Особое значение имеет единичная импульсная или дельта-функция. Она обозначается 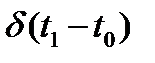
Дельта-функция обладает следующими свойствами:
Свойство (1.6) означает, что, несмотря на то, что функция имеет пренебрежимо малую длительность, площадь, ограниченная ей, имеет конечное значение, равное 1.
Свойство (1.7) означает, что импульсная функция 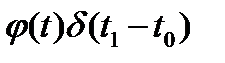
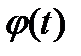
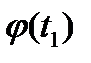
3. Периодическое возмущение. В ряде случаев периодическое возмущение является наиболее удобным для исследования. Так, для автоматических систем, работающих в режиме незатухающих колебаний, целесообразно проводить проверку их свойств под действием периодических возмущений.
Стандартным считается периодическое возмущение единичной амплитуды x(t)=sin ωt.
Аналоговые и дискретные сигналы имеют некоторые общие характеристики, с помощью которых они описываются. К таким характеристикам относятся: динамический диапазон, время установления и ширина спектра сигнала.
Динамический диапазон характеризуется отношением наибольшей мгновенной (пиковой) мощности к наименьшей (пороговой) мощности. Динамический диапазон является чисто физической характеристикой сигнала и не отражает смысла передаваемой с помощью этого сигнала информации. Однако его выбор определяется максимально допустимыми искажениями, которым может подвергаться сигнал в процессе формирования, передачи, обработки и приема без потери заключенной в нем информации. Наименьшая (пороговая) мощность сигнала определяется уровнем шумов и помех, которые неизбежно присутствуют в виде колебаний и скачков питающего напряжения, тепловых шумов, наводок от излучения, электромагнитных полей и т. д. При этом сигнал должен быть таким, чтобы он четко различался на уровне помех. Увеличение сигнала приводит к росту отношения сигнал-помеха, однако максимальное (пиковое) значение сигнала ограничивается как ростом затрачиваемой мощности, так и предельными характеристиками элементов и устройств, через которые происходит передача сигналов. Насыщение этих элементов приводит к искажению передаваемых сигналов, а значит и заключенной в них информации.
Время установления является динамической характеристикой сигнала и определяется временем, за которое сигнал достигнет своего установившегося значения. Этот параметр непосредственно связан с временными характеристиками устройств, формирующих сигнал, и определяется их инерционностью. Время установления можно характеризовать либо функцией времени (временной характеристикой), описывающей реальный процесс, либо функцией частоты (спектром, или рядом гармонических колебаний). При этом оба представления равносильны и взаимно дополняют друг друга, а переход от одного к другому осуществляется с помощью прямого и обратного преобразования Фурье или Лапласа.
Выбор того или иного способа описания (временного или частотного) определяется исключительно назначением устройства. При этом меняется лишь точка зрения на предмет, но не сам предмет, который представляет собой объективную реальность, независимую от способа ее описания.
Кроме рассмотренных общих характеристик, различные виды сигналов характеризуются рядом дополнительных, детализирующих их параметров. У постоянного напряжения – это амплитуда, у переменного напряжения – амплитуда, частота, фаза, среднее и действующее значения. Импульсные сигналы более сложны по форме, поэтому опишем их более детально.
Амплитудная модуляция: определение, графики, схемы, формулы
«Амплитудной модуляцией» называется изменение амплитуды несущего сигнала в соответствии с модулированным колебанием. Например, имеем высокочастотное несущее колебание (Формула) и первичный сигнал (Формула), где U0 — постоянная составляющая. Результирующий амплитудно-модулированный сигнал получим на основе перемножения несущего колебания и первичного сигнала:
Пусть x(t) является гармоническим колебанием с частотой Ω, т.е. х(t) = XcosΩt. Тогда (Формула). Здесь x(t) — медленно меняющаяся во времени функция по сравнению с высокочастотным колебанием ω0, т. е. Ω
— максимальное приращение амплитуды огибающей.
ВременнЫе диаграммы, иллюстрирующие процесс амплитудной модуляции тональным колебанием, показаны на рис. 4.1.
Рис. 4.1. ВременнЫе диаграммы, иллюстрирующие амплитудную модуляцию:
а — первичный сигнал; б — высокочастотное несущее колебание; в — модулированный сигнал
Коэффициентом модуляции называется отношение амплитуды (Формула) огибающей к амплитуде (Формула) несущего колебания, т. е. (Формула). Обычно 0
Раскроем данное выражение, что позволит определить спектр АМ-сигнала:
Из этого выражения видно, что АМ-колебание, спектр которого при модуляции одним гармоническим сигналом изображен на рис. 4.2, содержит три составляющие.
Из сказанного можно сделать следующие выводы.
На практике однотональные АМ-сигналы используются крайне редко. Более реален случай, когда низкочастотный модулированный сигнал имеет сложный спектральный состав:
Здесь частоты (Формула) образуют упорядоченную возрастающую последовательность (Формула), а амплитуды Хk и фазы φk — произвольные.
В этом случае для АМ-сигнала можно записать следующее аналитическое соотношение:

где (Формула) — парциальные коэффициенты модуляции, представляющие собой коэффициенты модуляции соответствующих компонентов первичного сигнала.
Рис. 4.2. Спектр колебаний при амплитудной модуляции одним низкочастотным гармоническим сигналом
Спектральное разложение производится так же, как и для однотонального АМ-сигнала:
Из этого разложения видно, что в спектре кроме несущего колебания содержатся группы верхних и нижних боковых колебаний. При этом спектр верхних боковых колебаний является копией спектра модулирующего сигнала, сдвинутой в область высоких частот на значение ω0, а спектр нижних боковых колебаний располагается зеркально относительно ω0.
Спектры исходного полосового сигнала и амплитудно-модулированного сигнала показаны на рис. 4.3.
Амплитудно-частотная характеристика (АЧХ). Спектр сигнала.
При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы и как с ними работать? В этом нам и предстоит сегодня разобраться 🙂 Кроме того, мы рассмотрим важнейшее понятие — амплитудно-частотную характеристику (АЧХ) сигналов.
Гармонические и негармонические сигналы.
Здесь A — амплитуда сигнала, w — циклическая частота, а \phi — начальная фаза. Вы спросите — а как же синус? Разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sin\alpha = cos(\frac<\pi><2>\medspace-\medspace \alpha) — то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний 🙂
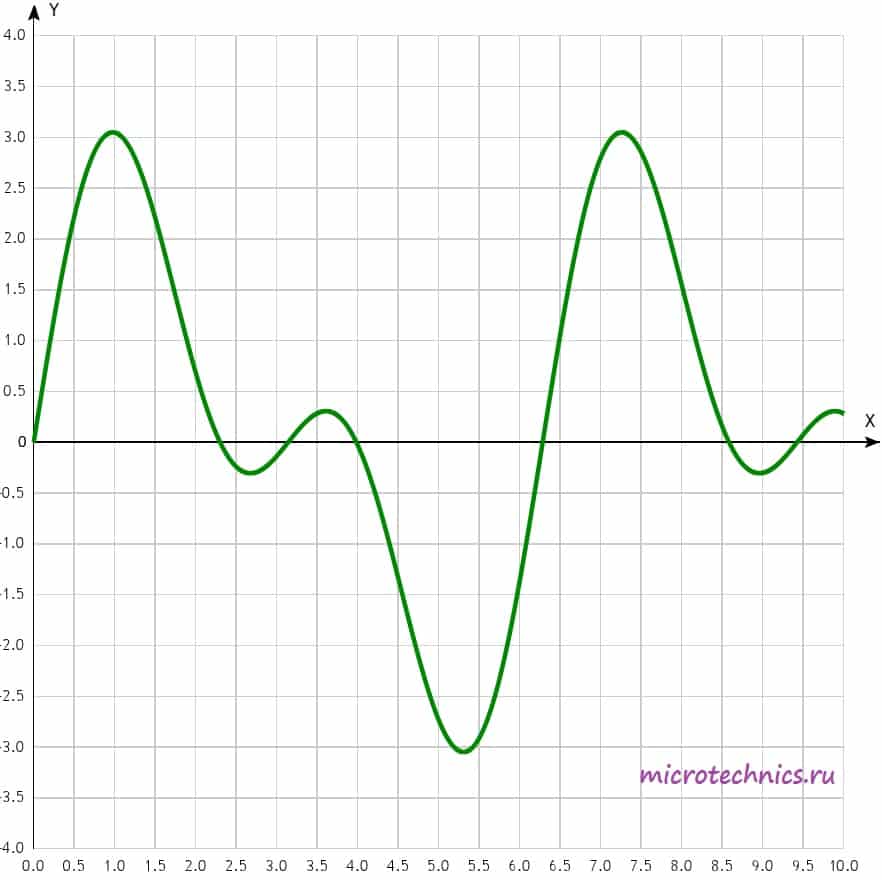
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
Как видите, несмотря на «нестандартную» форму, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
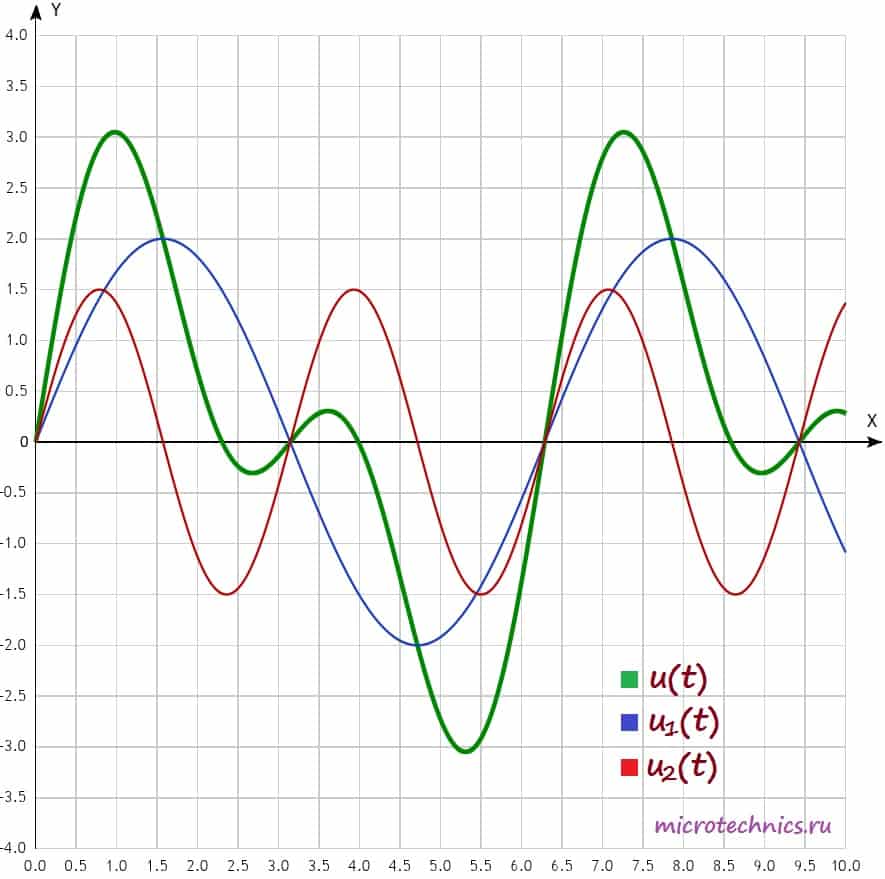
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть методики состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что давайте рассмотрим практический пример и разберемся чуть подробнее 🙂 Для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
Давайте изобразим все эти сигналы на одном графике:
В этой формуле U_k — амплитуда, а \phi_k — начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и видим в этой формуле 🙂 U_0 — это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите — среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0.
Амплитудный спектр сигнала.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:
Давайте рассмотрим амплитудный спектр поподробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
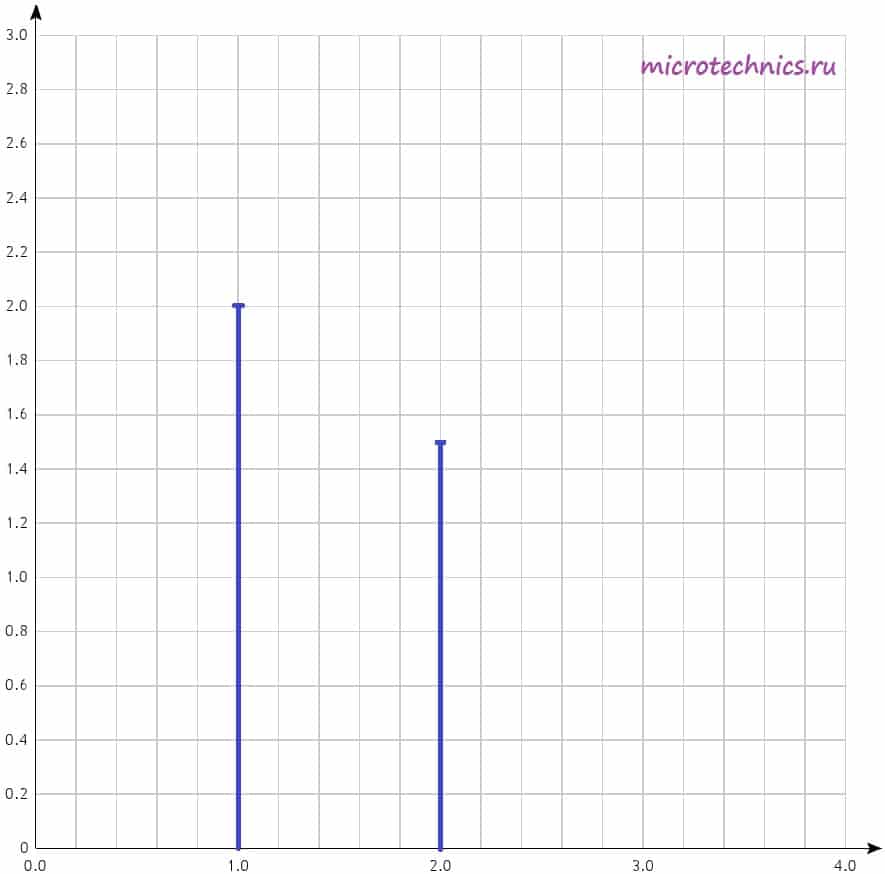
По горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси — амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались! Давайте перейдем к следующей теме сегодняшней статьи — к понятию амплитудно-частотной характеристики.
Амплитудно-частотная характеристика (АЧХ).
АЧХ является важнейшей характеристикой многих цепей и устройств — фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Что же она показывает?
АЧХ — это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но нас сейчас интересует, в первую очередь, аудио-сигнал, и выглядит он следующим образом:
Как видите, ни о какой периодичности здесь не идет и речи! Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи 🙂 Просто примем тот факт, что они позволяют нам осуществить такое преобразование с аудио-сигналом.
Соответственно, мы можем построить диаграмму амплитудного спектра звукового сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте обсудим этот момент чуть поподробнее…
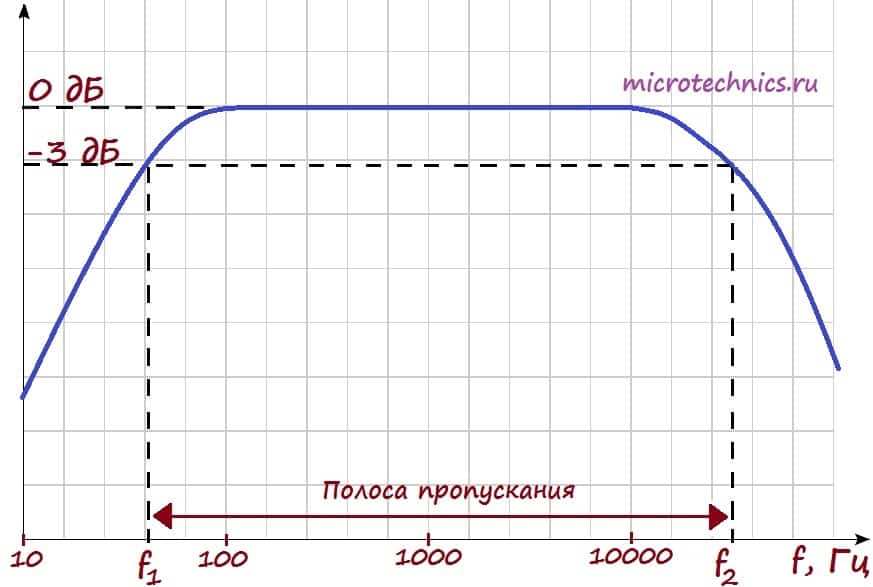
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:
Разберемся поэтапно, что же тут изображено… Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы откладываем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.
По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.
Практические примеры АЧХ аудио-устройств.
Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:
Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье 🙂
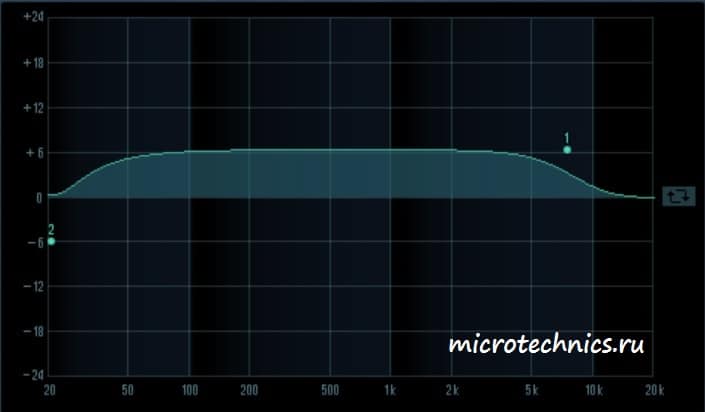
В завершении статьи посмотрим на пару АЧХ, полученных в программном эквалайзере:
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.
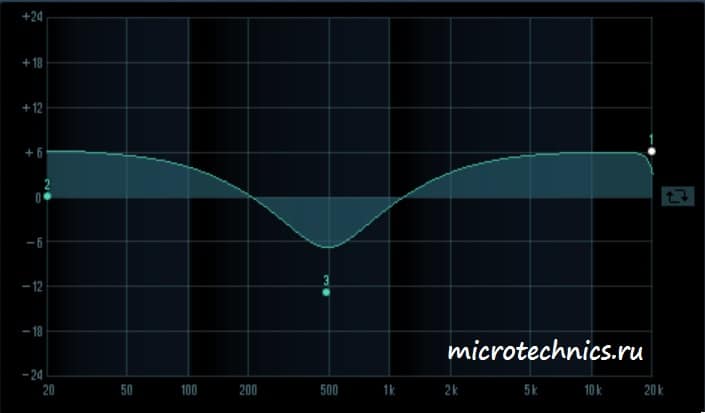
А здесь ситуация совсем другая — низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.
А здесь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов 🙂
На этом мы заканчиваем нашу сегодняшнюю статью… Спасибо за внимание и ждем вас на нашем сайте снова!
Что приводит под одну амплитуду принимаемые сигналы
Сигналы, поступающие из источника сообщений (микрофон, передающая телевизионная камера, датчик телеметрической системы), как правило, не могут быть непосредственно переданы по радиоканалу. Дело не только в том, что эти сигналы недостаточно велики по амплитуде. Гораздо существеннее их Относительная низкочастотностъ. Чтобы осуществить эффективную передачу сигналов в какой-либо среде, необходимо перемести спектр этих сигналов из низкочастотной области в область достаточно высоких частот. Данная процедура получила в радиотехнике название модуляции.
4.1. Сигналы с амплитудной модуляцией
Прежде чем изучать этот простейший вид модулированных сигналов, рассмотрим кратко некоторые вопросы, касающиеся принципов модуляции любого вида.
Понятие несущего колебания. Идея способа, позволяющего переносить спектр сигнала в область высоких частот, заключается в следующем. Прежде всего в передатчике формируется вспомогательный высокочастотный сигнал, называемый несущим колебанием. Его математическая модель 


Физический процесс управления параметрами несущего колебания и является модуляцией.
В радиотехнике широкое распространение получили системы модуляции, использующие в качестве несущего простое гармоническое колебание
имеющее три свободных параметра
Изменяя во времени тот или иной параметр, можно получать различные виды модуляции.
Принцип амплитудной модуляции.
Если переменной оказывается амплитуда сигнала 


Осциллограмма АМ-сигнала имеет характерный вид (см. рис. 4.1). Обращает на себя внимание симметрия графика относительно оси времени. В соответствии с формулой (4.2) AM-сигнал есть произведение огибающей 

Рис. 4.1. АМ-сигналы при различных глубинах модуляции: а — неглубокая модуляция: б — глубокая модуляция; в — перемодуляция
При амплитудной модуляции связь между огибающей 

Здесь 
Величина М характеризует глубину амплитудной модуляции. Смысл этого термина поясняется осциллограммами АМ-сигналов, изображенными на рис. 4.1, а-в.
При малой глубине модуляции относительное изменение огибающей невелико, т. е. 
Если же в моменты времени, когда сигнал 
то говорят о глубокой амплитудной модуляции. Иногда вводят дополнительно относительный коэффициент модуляции вверх
и относительный коэффициент модуляции вниз
AM-сигналы с малой глубиной модуляции в радиоканалах нецелесообразны ввиду неполного использования мощности передатчика.
В то же время 100%-ная модуляция вверх 
Не менее опасна слишком глубокая амплитудная модуляция вниз. На рис. 4.1, в изображена так называемая перемодуляция 
Однотональная амплитудная модуляция.
Простейший АМ-сигнал может быть получен в случае, когда модулирующим низкочастотным сигналом является гармоническое колебание с частотой 
называется однотоншьным АМ-сигналом.
Выясним, можно ли такой сигнал представить как сумму простых гармонических колебаний с различными частотами. Используя известную тригонометрическую формулу произведения косинусов, из выражения (4.4) сразу получаем
Формула (4.5) устанавливает спектральный состав однотонального АМ-сигнала. Принята следующая терминология: 


Строя по формуле (4.5) спектральную диаграмму однотонального АМ-сигнала, следует прежде всего обратить внимание на равенство амплитуд верхнего и нижнего боковых колебаний, а также на симметрию расположения этих спектральных составляющих относительно несущего колебания.
Энергетические характеристики АМ-сигнала.
Рассмотрим вопрос о соотношении мощностей несущего и боковых колебаний. Источник однотонального АМ-сигнала эквивалентен трем последовательно включенным источникам гармонических колебаний:
Положим для определенности, что это источники ЭДС, соединенные последовательно и нагруженные на единичный резистор. Тогда мгновенная мощность АМ-сигнала будет численно равна квадрату суммарного напряжения:
Чтобы найти среднюю мощность сигнала, величину 
Отсюда следует, что
Так, даже при 100%-ной модуляции (М = 1) доля мощности обоих боковых колебаний составляет всего лишь 50% от мощности смодулированного несущего колебания. Поскольку информация о сообщении заключена в боковых колебаниях, можно отметить неэффективность использования мощности при передаче АМ-сигнала.
Амплитудная модуляция при сложном модулирующем сигнале.
На практике однотональные AM-сигналы используются редко. Гораздо более реален случай, когда модулирующий низкочастотный сигнал имеет сложный спектральный состав. Математической моделью такого сигнала может быть, например, тригонометрическая сумма
Подставив формулу (4.9) в (4.3), получим
Введем совокупность парциальных (частичных) коэффициентов модуляции

и запишем аналитическое выражение сложномодудированного (многотонального) АМ-сигнала в форме, которая обобщает выражение (4.4):
Спектральное разложение проводится так же, как и для однотонального АМ-сигнала:
На рис. 4.2, а изображена спектральная диаграмма модулирующего сигнала 
Рис. 4.2. Спектральные диаграммы 
Итак, в спектре сложномодулированного АМ-сигнала, помимо несущего колебания, содержатся группы верхних и нижних боковых колебаний. Спектр верхних боковых колебаний является масштабной копией спектра модулирующего сигнала, сдвинутой в область высоких частот на величину 

Из сказанного следует важный вывод: ширина спектра АМ-сигнала равна удвоенному значению наивысшей частоты в спектре модулирующего низкочастотного сигнала.
Пример 4.1. Оценить число вещательных радиоканалов, которые можно разместить в диапазоне частот от 0.5 до 1.5 МГц (примерные границы средневолнового вещательного диапазона).
Для удовлетворительного воспроизведения сигналов радиовещания необходимо воспроизводить звуковые частоты от 100 Гц до 12 кГц. Таким образом, полоса частот, отводимая одному АМ-каналу, равна 24 кГц. Чтобы избежать перекрестных помех между каналами, следует предусмотреть защитный интервал шириной в 1 кГц. Поэтому допустимое число каналов
Амплитудно-манипулированные сигналы.
Важным классом многотональных АМ-сигналов являются так называемые манипулированные сигналы. В простейшем случае это — последовательности радиоимпульсов, отделенных друг от друга паузами. Такие сигналы используются в радиотелеграфии и в системах передачи дискретной информации по радиоканалам.
Если s(t) — функция, в каждый момент времени принимающая значение либо 0, либо 1, то амплитудио-манипулированный сигнал представляется в виде
Пусть, например, функция 

где q — скважность последовательности.
Векторная диаграмма АМ-сигнала.
Иногда полезным может оказаться графическое изображение АМ-сигнала посредством суммы векторов, вращающихся в комплексной плоскости.
Для простоты рассмотрим одиотональную модуляцию. Мгновенное значение несущего колебания 


Верхнее боковое колебание отображается на диаграмме вектором 


Такой же вектор для нижнего бокового колебания отличается лишь знаком в выражении для его фазового угла. Итак, на комплексной плоскости необходимо построить сумму трех векторов
Легко видеть, что эта сумма будет ориентирована вдоль вектора йнес. Мгновенное значение АМ-сигнала при 
С течением времени, помимо отмеченного вращения оси отсчета углов, будут наблюдаться следующие трансформации чертежа (рис. 4.3,6): 1) вектор 




Строя суммарный вектор 

Балансная амплитудная модуляция.
Как было показано, значительная доля мощности обычного АМ-сигнала сосредоточена в несущем колебании. Для более эффективного использования мощности передатчика можно формировать АМ-сигналы с подавленным несущим колебанием, реализуя так называемую балайсную амплитудную модуляцию. На основании формулы (4.4) представление однотонального АМ-сигнала с балансной модуляцией таково:
Имеет место перемножение двух сигналов — модулирующего и несущего. Колебания вида (4.16) с физической точки зрения являются биениями двух гармонических сигналов с одинаковыми амплитудами 
При многотональной балансной модуляции аналитическое выражение сигнала принимает вид
Как и при обычной амплитудной модуляции, здесь наблюдаются две симметричные группы верхних и ннжних боковых колебаний.
Если рассмотреть осциллограмму биений, может показаться неясным, почему в спектре этого сигнала нет несущей частоты, хотя налицо присутствие высокочастотного заполнения, изменяющегося во времени именно с этой частотой.
Дело в том, что при переходе огибающей биений через нуль фаза высокочастотного заполнения скачком изменяется на 180°, поскольку функция 


Однополосная амплитудная модуляция.
Еще более интересное усовершенствование принципа обычной амплитудной модуляции заключается в формировании сигнала с подавленной верхней или нижней боковой полосой частот.
Сигналы с одной боковой полосой (ОБП или SSB-сигналы — от англ. single sideband) по внешним характеристикам напоминают обычные AM-сигналы. Например, однотональный ОБП-сигнал с подавленной нижней боковой частотой записывается в виде
Проводя тригонометрические преобразования, получаем
Два последних слагаемых представляют собой произведение двух функций, одна из которых изменяется во времени медленно, а другая — быстро. Принимая во внимание, что «быстрые» сомножители находятся по отношению друг к другу во временной квадратуре, вычисляем медленно изменяющуюся огибающую ОБП-сигнала:
Рис. 4.4. Огибающие однотональных модулированных сигналов при 
График огибающей ОБП-сигнала, рассчитанный по формуле (4.18) при 
Сравнение приведенных кривых показывает, что непосредственная демодуляция ОБП-сигнала по его огибающей будет сопровождаться значительными искажениями.
Дальнейшим усовершенствованием систем ОБП является частичное или полное подавление несущего колебания. При этом мощность передатчика используется еще более эффективно.
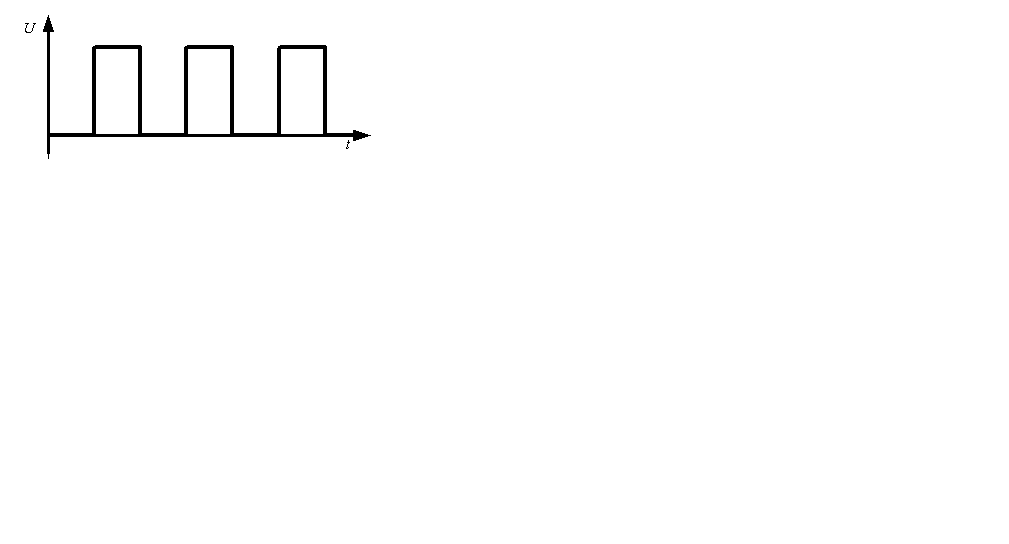
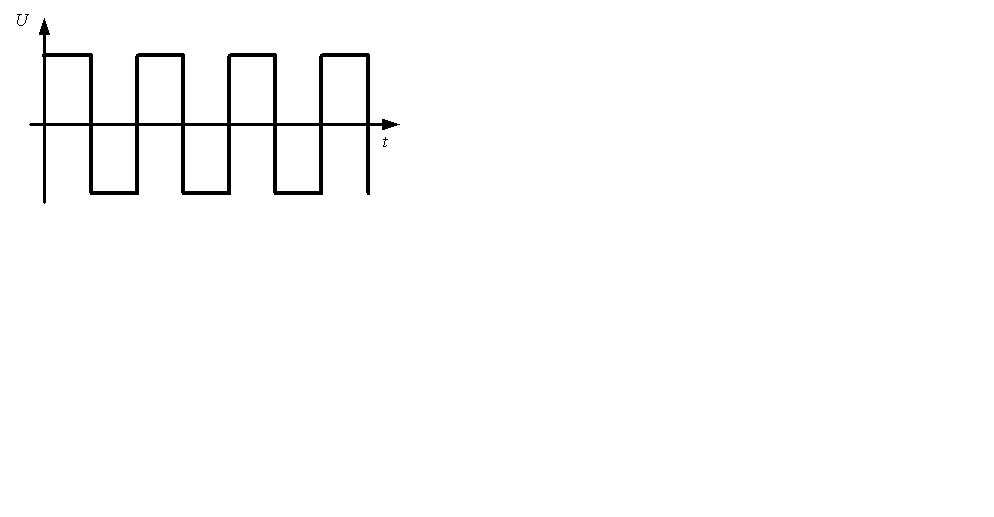
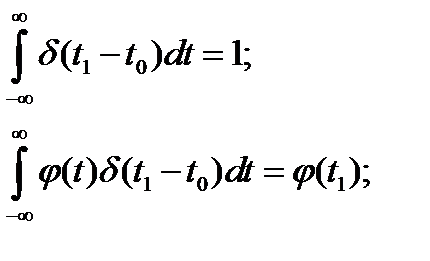

 — максимальное приращение амплитуды огибающей.
— максимальное приращение амплитуды огибающей.