что такое предикторы в машинном обучении
Введение в машинное обучение
1.1 Введение
Благодаря машинному обучению программист не обязан писать инструкции, учитывающие все возможные проблемы и содержащие все решения. Вместо этого в компьютер (или отдельную программу) закладывают алгоритм самостоятельного нахождения решений путём комплексного использования статистических данных, из которых выводятся закономерности и на основе которых делаются прогнозы.
Технология машинного обучения на основе анализа данных берёт начало в 1950 году, когда начали разрабатывать первые программы для игры в шашки. За прошедшие десятилетий общий принцип не изменился. Зато благодаря взрывному росту вычислительных мощностей компьютеров многократно усложнились закономерности и прогнозы, создаваемые ими, и расширился круг проблем и задач, решаемых с использованием машинного обучения.
Чтобы запустить процесс машинного обучение, для начала необходимо загрузить в компьютер Датасет(некоторое количество исходных данных), на которых алгоритм будет учиться обрабатывать запросы. Например, могут быть фотографии собак и котов, на которых уже есть метки, обозначающие к кому они относятся. После процесса обучения, программа уже сама сможет распознавать собак и котов на новых изображениях без содержания меток. Процесс обучения продолжается и после выданных прогнозов, чем больше данных мы проанализировали программой, тем более точно она распознает нужные изображения.
Благодаря машинному обучению компьютеры учатся распознавать на фотографиях и рисунках не только лица, но и пейзажи, предметы, текст и цифры. Что касается текста, то и здесь не обойтись без машинного обучения: функция проверки грамматики сейчас присутствует в любом текстовом редакторе и даже в телефонах. Причем учитывается не только написание слов, но и контекст, оттенки смысла и другие тонкие лингвистические аспекты. Более того, уже существует программное обеспечение, способное без участия человека писать новостные статьи (на тему экономики и, к примеру, спорта).
1.2 Типы задач машинного обучения
Все задачи, решаемые с помощью ML, относятся к одной из следующих категорий.
1)Задача регрессии – прогноз на основе выборки объектов с различными признаками. На выходе должно получиться вещественное число (2, 35, 76.454 и др.), к примеру цена квартиры, стоимость ценной бумаги по прошествии полугода, ожидаемый доход магазина на следующий месяц, качество вина при слепом тестировании.
2)Задача классификации – получение категориального ответа на основе набора признаков. Имеет конечное количество ответов (как правило, в формате «да» или «нет»): есть ли на фотографии кот, является ли изображение человеческим лицом, болен ли пациент раком.
3)Задача кластеризации – распределение данных на группы: разделение всех клиентов мобильного оператора по уровню платёжеспособности, отнесение космических объектов к той или иной категории (планета, звёзда, чёрная дыра и т. п.).
4)Задача уменьшения размерности – сведение большого числа признаков к меньшему (обычно 2–3) для удобства их последующей визуализации (например, сжатие данных).
5)Задача выявления аномалий – отделение аномалий от стандартных случаев. На первый взгляд она совпадает с задачей классификации, но есть одно существенное отличие: аномалии – явление редкое, и обучающих примеров, на которых можно натаскать машинно обучающуюся модель на выявление таких объектов, либо исчезающе мало, либо просто нет, поэтому методы классификации здесь не работают. На практике такой задачей является, например, выявление мошеннических действий с банковскими картами.
1.3 Основные виды машинного обучения
Основная масса задач, решаемых при помощи методов машинного обучения, относится к двум разным видам: обучение с учителем (supervised learning) либо без него (unsupervised learning). Однако этим учителем вовсе не обязательно является сам программист, который стоит над компьютером и контролирует каждое действие в программе. «Учитель» в терминах машинного обучения – это само вмешательство человека в процесс обработки информации. В обоих видах обучения машине предоставляются исходные данные, которые ей предстоит проанализировать и найти закономерности. Различие лишь в том, что при обучении с учителем есть ряд гипотез, которые необходимо опровергнуть или подтвердить. Эту разницу легко понять на примерах.
Машинное обучение с учителем
Предположим, в нашем распоряжении оказались сведения о десяти тысячах московских квартир: площадь, этаж, район, наличие или отсутствие парковки у дома, расстояние от метро, цена квартиры и т. п. Нам необходимо создать модель, предсказывающую рыночную стоимость квартиры по её параметрам. Это идеальный пример машинного обучения с учителем: у нас есть исходные данные (количество квартир и их свойства, которые называются признаками) и готовый ответ по каждой из квартир – её стоимость. Программе предстоит решить задачу регрессии.
Ещё пример из практики: подтвердить или опровергнуть наличие рака у пациента, зная все его медицинские показатели. Выяснить, является ли входящее письмо спамом, проанализировав его текст. Это всё задачи на классификацию.
Машинное обучение без учителя
В случае обучения без учителя, когда готовых «правильных ответов» системе не предоставлено, всё обстоит ещё интереснее. Например, у нас есть информация о весе и росте какого-то количества людей, и эти данные нужно распределить по трём группам, для каждой из которых предстоит пошить рубашки подходящих размеров. Это задача кластеризации. В этом случае предстоит разделить все данные на 3 кластера (но, как правило, такого строгого и единственно возможного деления нет).
Если взять другую ситуацию, когда каждый из объектов в выборке обладает сотней различных признаков, то основной трудностью будет графическое отображение такой выборки. Поэтому количество признаков уменьшают до двух или трёх, и становится возможным визуализировать их на плоскости или в 3D. Это – задача уменьшения размерности.
1.4 Основные алгоритмы моделей машинного обучения
1. Дерево принятия решений
Это метод поддержки принятия решений, основанный на использовании древовидного графа: модели принятия решений, которая учитывает их потенциальные последствия (с расчётом вероятности наступления того или иного события), эффективность, ресурсозатратность.
Для бизнес-процессов это дерево складывается из минимального числа вопросов, предполагающих однозначный ответ — «да» или «нет». Последовательно дав ответы на все эти вопросы, мы приходим к правильному выбору. Методологические преимущества дерева принятия решений – в том, что оно структурирует и систематизирует проблему, а итоговое решение принимается на основе логических выводов.
2. Наивная байесовская классификация
Наивные байесовские классификаторы относятся к семейству простых вероятностных классификаторов и берут начало из теоремы Байеса, которая применительно к данному случаю рассматривает функции как независимые (это называется строгим, или наивным, предположением). На практике используется в следующих областях машинного обучения:
Всем, кто хоть немного изучал статистику, знакомо понятие линейной регрессии. К вариантам её реализации относятся и наименьшие квадраты. Обычно с помощью линейной регрессии решают задачи по подгонке прямой, которая проходит через множество точек. Вот как это делается с помощью метода наименьших квадратов: провести прямую, измерить расстояние от неё до каждой из точек (точки и линию соединяют вертикальными отрезками), получившуюся сумму перенести наверх. В результате та кривая, в которой сумма расстояний будет наименьшей, и есть искомая (эта линия пройдёт через точки с нормально распределённым отклонением от истинного значения).
Линейная функция обычно используется при подборе данных для машинного обучения, а метод наименьших квадратов – для сведения к минимуму погрешностей путем создания метрики ошибок.
4. Логистическая регрессия
Логистическая регрессия – это способ определения зависимости между переменными, одна из которых категориально зависима, а другие независимы. Для этого применяется логистическая функция (аккумулятивное логистическое распределение). Практическое значение логистической регрессии заключается в том, что она является мощным статистическим методом предсказания событий, который включает в себя одну или несколько независимых переменных. Это востребовано в следующих ситуациях:
Это целый набор алгоритмов, необходимых для решения задач на классификацию и регрессионный анализ. Исходя из того что объект, находящийся в N-мерном пространстве, относится к одному из двух классов, метод опорных векторов строит гиперплоскость с мерностью (N – 1), чтобы все объекты оказались в одной из двух групп. На бумаге это можно изобразить так: есть точки двух разных видов, и их можно линейно разделить. Кроме сепарации точек, данный метод генерирует гиперплоскость таким образом, чтобы она была максимально удалена от самой близкой точки каждой группы.
SVM и его модификации помогают решать такие сложные задачи машинного обучения, как сплайсинг ДНК, определение пола человека по фотографии, вывод рекламных баннеров на сайты.
Он базируется на алгоритмах машинного обучения, генерирующих множество классификаторов и разделяющих все объекты из вновь поступающих данных на основе их усреднения или итогов голосования. Изначально метод ансамблей был частным случаем байесовского усреднения, но затем усложнился и оброс дополнительными алгоритмами:
Кластеризация заключается в распределении множества объектов по категориям так, чтобы в каждой категории – кластере – оказались наиболее схожие между собой элементы.
Кластеризировать объекты можно по разным алгоритмам. Чаще всего используют следующие:
8. Метод главных компонент (PCA)
Метод главных компонент, или PCA, представляет собой статистическую операцию по ортогональному преобразованию, которая имеет своей целью перевод наблюдений за переменными, которые могут быть как-то взаимосвязаны между собой, в набор главных компонент – значений, которые линейно не коррелированы.
Практические задачи, в которых применяется PCA, – визуализация и большинство процедур сжатия, упрощения, минимизации данных для того, чтобы облегчить процесс обучения. Однако метод главных компонент не годится для ситуаций, когда исходные данные слабо упорядочены (то есть все компоненты метода характеризуются высокой дисперсией). Так что его применимость определяется тем, насколько хорошо изучена и описана предметная область.
9. Сингулярное разложение
В линейной алгебре сингулярное разложение, или SVD, определяется как разложение прямоугольной матрицы, состоящей из комплексных или вещественных чисел. Так, матрицу M размерностью [m*n] можно разложить таким образом, что M = UΣV, где U и V будут унитарными матрицами, а Σ – диагональной.
Одним из частных случаев сингулярного разложения является метод главных компонент. Самые первые технологии компьютерного зрения разрабатывались на основе SVD и PCA и работали следующим образом: вначале лица (или другие паттерны, которые предстояло найти) представляли в виде суммы базисных компонент, затем уменьшали их размерность, после чего производили их сопоставление с изображениями из выборки. Современные алгоритмы сингулярного разложения в машинном обучении, конечно, значительно сложнее и изощрённее, чем их предшественники, но суть их в целом нем изменилась.
10. Анализ независимых компонент (ICA)
Это один из статистических методов, который выявляет скрытые факторы, оказывающие влияние на случайные величины, сигналы и пр. ICA формирует порождающую модель для баз многофакторных данных. Переменные в модели содержат некоторые скрытые переменные, причем нет никакой информации о правилах их смешивания. Эти скрытые переменные являются независимыми компонентами выборки и считаются негауссовскими сигналами.
В отличие от анализа главных компонент, который связан с данным методом, анализ независимых компонент более эффективен, особенно в тех случаях, когда классические подходы оказываются бессильны. Он обнаруживает скрытые причины явлений и благодаря этому нашёл широкое применение в самых различных областях – от астрономии и медицины до распознавания речи, автоматического тестирования и анализа динамики финансовых показателей.
1.5 Примеры применения в реальной жизни
Пример 1. Диагностика заболеваний
Пациенты в данном случае являются объектами, а признаками – все наблюдающиеся у них симптомы, анамнез, результаты анализов, уже предпринятые лечебные меры (фактически вся история болезни, формализованная и разбитая на отдельные критерии). Некоторые признаки – пол, наличие или отсутствие головной боли, кашля, сыпи и иные – рассматриваются как бинарные. Оценка тяжести состояния (крайне тяжёлое, средней тяжести и др.) является порядковым признаком, а многие другие – количественными: объём лекарственного препарата, уровень гемоглобина в крови, показатели артериального давления и пульса, возраст, вес. Собрав информацию о состоянии пациента, содержащую много таких признаков, можно загрузить её в компьютер и с помощью программы, способной к машинному обучению, решить следующие задачи:
Пример 2. Поиск мест залегания полезных ископаемых
В роли признаков здесь выступают сведения, добытые при помощи геологической разведки: наличие на территории местности каких-либо пород (и это будет признаком бинарного типа), их физические и химические свойства (которые раскладываются на ряд количественных и качественных признаков).
Для обучающей выборки берутся 2 вида прецедентов: районы, где точно присутствуют месторождения полезных ископаемых, и районы с похожими характеристиками, где эти ископаемые не были обнаружены. Но добыча редких полезных ископаемых имеет свою специфику: во многих случаях количество признаков значительно превышает число объектов, и методы традиционной статистики плохо подходят для таких ситуаций. Поэтому при машинном обучении акцент делается на обнаружение закономерностей в уже собранном массиве данных. Для этого определяются небольшие и наиболее информативные совокупности признаков, которые максимально показательны для ответа на вопрос исследования – есть в указанной местности то или иное ископаемое или нет. Можно провести аналогию с медициной: у месторождений тоже можно выявить свои синдромы. Ценность применения машинного обучения в этой области заключается в том, что полученные результаты не только носят практический характер, но и представляют серьёзный научный интерес для геологов и геофизиков.
Пример 3. Оценка надёжности и платёжеспособности кандидатов на получение кредитов
С этой задачей ежедневно сталкиваются все банки, занимающиеся выдачей кредитов. Необходимость в автоматизации этого процесса назрела давно, ещё в 1960–1970-е годы, когда в США и других странах начался бум кредитных карт.
Лица, запрашивающие у банка заём, – это объекты, а вот признаки будут отличаться в зависимости от того, физическое это лицо или юридическое. Признаковое описание частного лица, претендующего на кредит, формируется на основе данных анкеты, которую оно заполняет. Затем анкета дополняется некоторыми другими сведениями о потенциальном клиенте, которые банк получает по своим каналам. Часть из них относятся к бинарным признакам (пол, наличие телефонного номера), другие — к порядковым (образование, должность), большинство же являются количественными (величина займа, общая сумма задолженностей по другим банкам, возраст, количество членов семьи, доход, трудовой стаж) или номинальными (имя, название фирмы-работодателя, профессия, адрес).
Для машинного обучения составляется выборка, в которую входят кредитополучатели, чья кредитная история известна. Все заёмщики делятся на классы, в простейшем случае их 2 – «хорошие» заёмщики и «плохие», и положительное решение о выдаче кредита принимается только в пользу «хороших».
Более сложный алгоритм машинного обучения, называемый кредитным скорингом, предусматривает начисление каждому заёмщику условных баллов за каждый признак, и решение о предоставлении кредита будет зависеть от суммы набранных баллов. Во время машинного обучения системы кредитного скоринга вначале назначают некоторое количество баллов каждому признаку, а затем определяют условия выдачи займа (срок, процентную ставку и остальные параметры, которые отражаются в кредитном договоре). Но существует также и другой алгоритм обучения системы – на основе прецедентов.
Применение машинного обучения в трейдинге
Часть 1
В этой серии статей, я собираюсь шаг за шагом построить и оттестировать простую стратегию управления активом, основанную на машинном обучении. Первая часть будет посвящена базовым концепциям машинного обучения и их применению к финансовым рынкам.
Теперь давайте выберем алгоритм. Есть целый ряд алгоритмов, которые вы можете использовать, включая скрытые Марковские Модели, искусственные нейронные сети, наивный байесовский классификатор, метод опорных векторов, дерева решений, дисперсионный анализ и множество других. Здесь хороший список, где вы можете разобраться в каждом алгоритме и понять когда и какой из них применять. Для начала я рекомендую использовать один из наиболее часто используемых алгоритмов, например метод опорных векторов или наивный байесовский классификатор. Не тратьте много времени на выбор, наиболее важные части вашего анализа — индикаторы которые вы используете и величина, которую прогнозируете.
Часть 2
Теперь, когда мы разобрались с базовой концепцией использования алгоритмов машинного обучения в вашей стратегии, мы изучим простой пример использования наивного байесовского классификатора для предсказания направления акций Apple. Сначала мы разберемся с тем, как работает этот классификатор, затем мы рассмотрим очень простой пример использования дня недели для предсказания движения цены, а в конце мы усложним модель, добавив технический индикатор.
Что такое наивный байесовский классификатор?
Формула Байеса позволяет найти вероятность того, что событие А случится, если известно, что событие В уже произошло. Обычно обозначается как: P (A | B).
В нашем примере, мы спрашиваем: «Какова вероятность, что сегодняшняя цена повысится, если известно, что сегодня среда?». Метод учитывает как вероятность того, что сегодняшняя цена вырастет исходя из общего количества дней во время которых наблюдался рост, так и исходя из того, что сегодня среда, т. е. сколько раз цена росла в среду.
У нас появляется возможность сравнить вероятность того, что сегодняшняя цена вырастет и вероятность того, что она упадет, и использовать наибольшее значение как прогноз.
До сих пор мы обсуждали только один индикатор, но как только их становится несколько, вся математика быстро усложняется. Чтобы это предотвратить используется наивный байесовский классификатор (вот тут хорошая статья). Он обрабатывает каждый индикатор, как независимый, или не коррелированный (отсюда термин наивный). Поэтому важно использовать индикаторы связанные слабо или не связанные вовсе.
Это очень упрощенное описание наивного байесовского классификатора, если вам интересно узнать о нем подробнее, а так же о других алгоритмах машинного обучения, посмотрите тут
Пошаговый пример на R
Всего в тестовой выборке 164 дня. При этом предсказания нашей модели совпали с реальными данными 79 раз или в 48% случаев.
Этот результат нельзя назвать хорошим, но он должен дать вам представление о том, как построить свою собственную стратегию, основанную на машинном обучении. В следующей части, мы посмотрим, как можно использовать эту модель для улучшения вашей стратегии.
Примечание переводчика 5. На сегодняшний день есть еще 2 статьи из этого цикла: про дерево решений и про нейронные сети. Статьи в таком же стиле, т.е. не глубокие, а только дающие общее представление о вопросе. Если интересно — я продолжу переводить. Обо всех замечаниях, неточностях и прочих ошибках пишите в личку.
Big Data. Machine Learning. Data Science.
Блог компании Даталитика. Интересное об искусственном интеллекте, машинном обучении, больших данных и ИТ-консалтинге
Подготовка данных для алгоритмов машинного обучения
Описание стека и некоторые вводные
Первый взгляд на датасет и понимание его специфики
Трудно работать с данными, не понимая, что они из себя представляют, поэтому давайте их загрузим и выведем некоторые статистики.
Это даст нам первое представление о том, что есть наши данные. Далее посмотрим на размеры наших табличных данных. Выполнив построчно код ниже
Также было бы неплохо увидеть информацию о количестве каждого уникального значения для каждого столбца в наборе данных:
Большинство столбцов выглядят хорошо, но есть несколько нуждающихся в очистке. Примеры некорректных значений данных ниже.
Разделение на обучающую выборку и целевую переменную
Обработка пропусков в данных
| id | weather | temperature | humidity | play tennis? |
|---|---|---|---|---|
| 1 | cloudy | 60 | NaN | yes |
| 2 | rainy | 75 | 80% | NaN |
| 3 | cloudy | NaN | 50% | no |
| 4 | sunny | 65 | 40% | yes |
Если бы мы удалили все строки с отсутствующими значениями, осталась бы только одна строка, и наш предиктор всегда бы предполагал, что я должен играть в теннис, так как других вариантов, по которым он будет учиться, про не будет. Предположим, мы вместо этого решили заменить нулевое значение температуры в строке 3 средним. В этом случае температура строки 3 искусственно сообщалась бы равной 65. И это уже позволит при каких-то входных параметрах получать от алгоритма отрицательный результат.
Scikit-learn предоставляет реализацию для обработки пропусков
Поиск неявных дубликатов
Если бы требовалось создать механизм предварительной обработки, который мог бы очищать входящие данные, требовалось бы воспользоваться более умным подходом. Но так как наша задача — это работа с уже имеющемся датасетом, то мы просто используем этот подход с заменой определенных типов.
Обнаружение выбросов
Как уже упоминалось ранее, оказалось, что для Age существуют значения, которые кажутся ошибочными. Такие как отрицательный возраст или чрезвычайно большие целые числа, могут негативно повлиять на результат работы алгоритма машинного обучения, и нам нужно будет их устранить.
Для этого возьмем нашу эвристическую оценку, в каком возрасте могут работать люди: от 14 до 100 лет. И все величины, не попадающие в этот диапазон, преобразуем в формат Not-a-Number.
Эти нулевые значения затем могут быть обработаны с использованием описанного выше sklearn Imputer.
После определения диапазона для работающего человека, визуализируем распределение возраста, присутствующего в этом наборе данных.
Кодирование данных
Многие алгоритмы машинного обучения ожидают числовые входные данные, поэтому нам нужно выяснить способ представления наших категориальных данных численным образом.
Одним из решений этого было бы произвольное присвоение числового значения для каждой категории и отображение набора данных из исходных категорий в каждое соответствующее число. Например, давайте посмотрим на столбец «leave» (как легко вам взять отпуск по болезни для состояния психического здоровья?) В нашем наборе данных
Который возвращает следующие значения
Для кодирования этих данных, сопоставим каждое значение с числом.
Этот процесс известен как Label Encoding и sklearn может сделать это за нас.
Проблема с этим подходом заключается в том, что вы вводите порядок, который может отсутствовать в исходных данных. В нашем случае можно утверждать, что данные являются ранжированными («Very difficult» меньше «Somewhat difficult», который меньше «Very easy», который меньше «Somewhat easy»), но в большинстве своем категориальные данные не имеют порядка. Например, если у вас есть признак обозначающий вид животного, зачастую высказывание кошка больше собаки не имеет смысла. Опасность кодирования меток заключается в том, что ваш алгоритм может научиться отдавать предпочтение собак, кошкам из-за искусственных порядковых значений, введенных вами во время кодирования.
Общим решением для кодирования номинальных данных является one-hot-encoding.
Вместо того, чтобы заменять категориальное значение на числовое значение (кодирование меток), как показано ниже
| id | type | numerical |
|---|---|---|
| 1 | cat | 1 |
| 2 | dog | 2 |
| 3 | snake | 3 |
| 4 | cat | 1 |
| 5 | dog | 2 |
| 6 | turtle | 4 |
| 7 | dog | 2 |
Вместо этого мы создаем столбец для каждого значения и используем 1 и 0 для обозначения выражения каждого значения. Эти новые столбцы часто называются фиктивными переменными.
| id | type | is_cat | is_dog | is_snake | is_turtle |
|---|---|---|---|---|---|
| 1 | cat | 1 | 0 | 0 | 0 |
| 2 | dog | 0 | 1 | 0 | 0 |
| 3 | snake | 0 | 0 | 1 | 0 |
| 4 | cat | 1 | 0 | 0 | 0 |
| 5 | dog | 0 | 1 | 0 | 0 |
| 6 | turle | 0 | 0 | 0 | 1 |
| 7 | dog | 0 | 1 | 0 | 0 |
Вы можете выполнить one-hot-encoding непосредственно в Pandas или использовать sklearn, хотя sklearn немного более прозрачен, поскольку one-hot-encoding из него работает только для целых значений. В нашем примере (где входные данные представляют собой строки) нам нужно сначала выполнить кодировку меток, а затем one-hot-encoding.
Нормализация тренировочных данных
На этом этапе мы успешно очистили наши данные и превратили их в форму, которая подходит для алгоритмов машинного обучения. Однако на данном этапе мы должны рассмотреть вопрос о том, полезен ли какой-либо метод нормализации данных для нашего алгоритма. Это зависит от данных и алгоритма, который мы планируем реализовать.
ML алгоритмы, которые требуют нормализации данных:
Примечание: приведенные выше списки ни в коем случае не являются исчерпывающими, а просто служат примером.
Предположим, у вас есть набор данных с различными единицами: температура в Кельвине, относительная влажность и день года. Мы можем увидеть следующие диапазоны для каждой функции.
Когда вы смотрите на эти значения, вы интуитивно нормализуете значения. Например, вы знаете, что увеличение на 0,5 (=50%) для влажности намного более значимо, чем увеличение на 0,5 для температуры. И если мы не будем нормализовать эти данные, наш алгоритм может научиться использовать температуру в качестве основного предиктора просто потому, что масштаб является наибольшим (и, следовательно, изменения в значениях температуры наиболее значительны для алгоритма). Нормализация данных позволяет всем признакам вносить одинаковый вклад (или, что более точно, позволяет добавлять признаки в зависимости от их важности, а не их масштаба).
Алгоритм нормализации
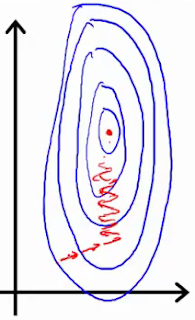
Если вы используете такой инструмент, как градиентный спуск, для оптимизации алгоритма, нормализация данных позволяет проводить последовательное обновление весов во всех измерениях.
Первое изображение представляет две функции с разными шкалами, в то время как последняя представляет собой нормализованное пространство признаков. Оптимизация градиентным спуском в первом случае может занять большее количество времени и в конечном итоге не прийти к минимуму.
Существует несколько различных методов нормализации данных, самые популярные из них:
Нормализация Min-max устанавливает наименьшее наблюдаемое значение равным 0, а наибольшее наблюдаемое значение — 1.
Для выполнения нормализации мы можем использовать функции в sklearn.
Несколько замечаний по этой реализации:
На практике вы можете выбрать только определенные столбцы. Например, вам не нужно нормализовать фиктивные переменные из one-hot-encoding.
Разделение данных для обучения и тестирования
Разделение данных на две подвыборки
Одной из последних вещей, которые нам нужно будет сделать, чтобы подготовить данные для обучения, является разделение данных на обучающую и тестовую выборку. Выделение тестовой выборки необходимо для понимания того, что мы обучили алгоритм в достаточной степени (не произошло переобучение или недообучение)