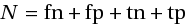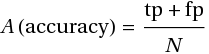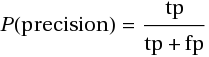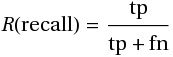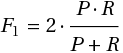f мера машинное обучение
Оценка точности классификатора
Начну с начала. Наша задача состоит в том, чтобы определить, какой классификатор лучше. Для этого нам нужна какая-то численная характеристика качества классификации.
Обычно про это рассказывают на примере бинарной классификации (типа спам/не-спам). Я же предлагаю взглянуть на проблему шире. Это, как мне кажется, позволяет лучше понять суть дела.
Давайте рассмотрим классификацию осадков. Пусть у нас есть наблюдения за 10 дней. И прогноз, который сгенерировал наш классификатор.
Количества пар [фактические осадки]-[предсказанные отсадки] мы можем представить наглядно в таблице — матрице неточностей (confusion matrix).
Самая простая мера качества классификатора — accuracy
Она равна отношения количества правильных решений и общего количества рассмотренных элементов. В терминах наших матриц: это отношение суммы диагональных ячеек к сумме всех ячеек. Оба классификатора показывают
Сразу виден недостаток такой оценки. Согласно ей, классифкаторы одинаковы. Однако, посмотрите на то, как они предсказывают снег. Видно, что первый намного лучше. Он только чуть-чуть наврал с ясной погодой, но снег он предсказал. Второй же классификатор ни разу не угадал снег. А «ясно» он предсказывает всего лишь чуть лучше.
Мы же не можем различить эти два классификатора с помощью нашей метрики accuracy.
Чтобы избавиться от этой проблемы вводят две другие метрики.
Точность (precision) и полнота (recall) классификатора
Точность (precision) — это отношение диагонального элемента и суммы всех элементов соответствующей строки. То есть, какая часть предсказаний этого класса была верна.
По смыслу, это «меткость» классификатора. На сколько часто он попадает в факт, когда работает в данном классе.
Полнота (recall) — это тоже самое, но только для столбца. То есть, какая доля фактических событий этого класса была правильно предсказана.
По смыслу, это «отзывчивость» классификатора. На сколько он «чувствует» факт.
Для наших классификаторов мы получим такие цифры:
Тут уже видно, что прогнозатор А лучше, чем В. Но нам-то нужно одно число для оценки.
И таким числом часто становится
F-мера
Нам нужна некоторая функция наших двух чисел, которая возрастала бы при росте любого из аргументов. Простейший кандидат и есть F-мера:
Для нашего классификатора А она будет равна 0.72, а для B — 0.59.
Теперь точно видно, что А выигрывает.
Кроме F-меры бывают и другие варианты функций, которые отдают предпочтения точности, или полноте. Но это уже другая история.
Оценка классификатора (точность, полнота, F-мера)
Продолжая тему реализации автоматической классификации необходимо обсудить следующий очень важный вопрос. Как оценивать качество алгоритма? Допустим, вы хотите внести изменения в алгоритм. Откуда вы знаете что эти изменения сделают алгоритм лучше? Конечно же надо проверять алгоритм на реальных данных.
Тестовая выборка
Основой проверки является тестовая выборка в которой проставлено соответствие между документами и их классами. В зависимости от ваших конкретных условий получение подобной выборки может быть затруднено, так как зачастую ее составляют люди. Но иногда ее можно получить без большого объема ручной работы, если проявить изобретательность. Каких-то конеретных рецептов, к сожалению, не существует.
Когда у вас появилась тестовая выборка достаточно натравить классификатор на документы и соотнести его решение с заведомо известным правильным решением. Но для того чтобы принимать решение хуже или лучше справляется с работой новая версия алгоритма нам необходима численная метрика его качества.
Численная оценка качества алгоритма
Accuracy
В простейшем случае такой метрикой может быть доля документов по которым классификатор принял правильное решение.
где, – количество документов по которым классификатор принял правильное решение, а – размер обучающей выборки. Очевидное решение, на котором для начала можно остановиться.
Тем не менее, у этой метрики есть одна особенность которую необходимо учитывать. Она присваивает всем документам одинаковый вес, что может быть не корректно в случае если распределение документов в обучающей выборке сильно смещено в сторону какого-то одного или нескольких классов. В этом случае у классификатора есть больше информации по этим классам и соответственно в рамках этих классов он будет принимать более адекватные решения. На практике это приводит к тому, что вы имеете accuracy, скажем, 80%, но при этом в рамках какого-то конкретного класса классификатор работает из рук вон плохо не определяя правильно даже треть документов.
Один выход из этой ситуации заключается в том чтобы обучать классификатор на специально подготовленном, сбалансированном корпусе документов. Минус этого решения в том что вы отбираете у классификатора информацию об отностельной частоте документов. Эта информация при прочих равных может оказаться очень кстати для принятия правильного решения.
Другой выход заключается в изменении подхода к формальной оценке качества.
Точность и полнота
Точность (precision) и полнота (recall) являются метриками которые используются при оценке большей части алгоритмов извлечения информации. Иногда они используются сами по себе, иногда в качестве базиса для производных метрик, таких как F-мера или R-Precision. Суть точности и полноты очень проста.
Точность системы в пределах класса – это доля документов действительно принадлежащих данному классу относительно всех документов которые система отнесла к этому классу. Полнота системы – это доля найденных классфикатором документов принадлежащих классу относительно всех документов этого класса в тестовой выборке.
Эти значения легко рассчитать на основании таблицы контингентности, которая составляется для каждого класса отдельно.
В таблице содержится информация сколько раз система приняла верное и сколько раз неверное решение по документам заданного класса. А именно:
Тогда, точность и полнота определяются следующим образом:
Рассмотрим пример. Допустим, у вас есть тестовая выборка в которой 10 сообщений, из них 4 – спам. Обработав все сообщения классификатор пометил 2 сообщения как спам, причем одно действительно является спамом, а второе было помечено в тестовой выборке как нормальное. Мы имеем одно истино-положительное решение, три ложно-отрицательных и одно ложно-положительное. Тогда для класса “спам” точность классификатора составляет (50% положительных решений правильные), а полнота (классификатор нашел 25% всех спам-сообщений).
Confusion Matrix
На практике значения точности и полноты гораздо более удобней рассчитывать с использованием матрицы неточностей (confusion matrix). В случае если количество классов относительно невелико (не более 100-150 классов), этот подход позволяет довольно наглядно представить результаты работы классификатора.
Матрица неточностей – это матрица размера N на N, где N — это количество классов. Столбцы этой матрицы резервируются за экспертными решениями, а строки за решениями классификатора. Когда мы классифицируем документ из тестовой выборки мы инкрементируем число стоящее на пересечении строки класса который вернул классификатор и столбца класса к которому действительно относится документ.
Матрица неточностей (26 классов, результирующая точность – 0.8, результирующая полнота – 0.91)
Как видно из примера, большинство документов классификатор определяет верно. Диагональные элементы матрицы явно выражены. Тем не менее в рамках некоторых классов (3, 5, 8, 22) классификатор показывает низкую точность.
Имея такую матрицу точность и полнота для каждого класса рассчитывается очень просто. Точность равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота – отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
F-мера
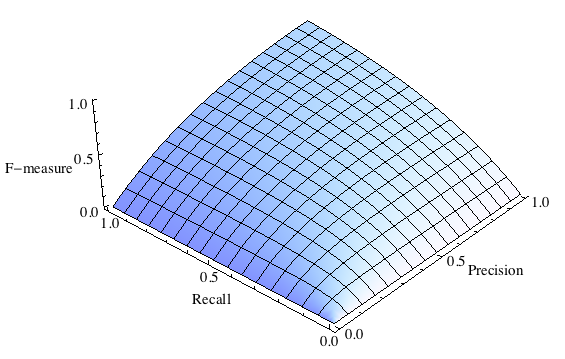
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма.
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют F1).
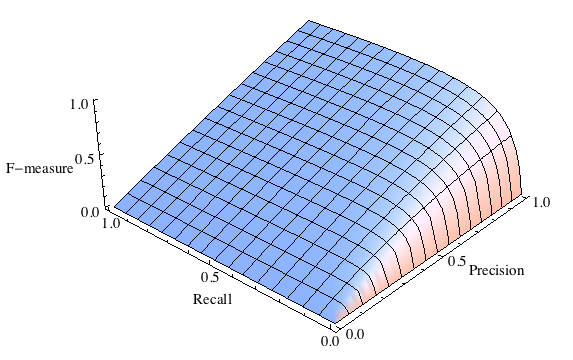
F-мера с приоритетом точности ()
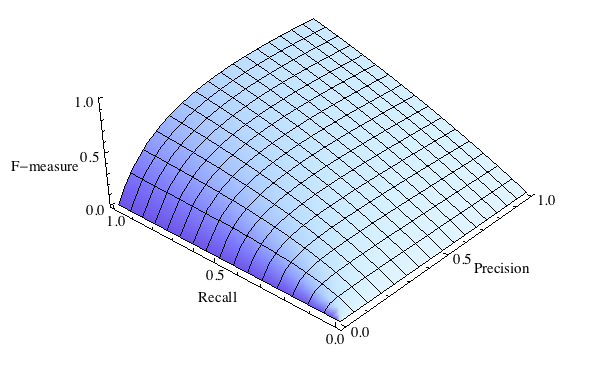
F-мера с приоритетом полноты ()
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея в своем распоряжении подобный механизм оценки вам будет гораздо проще принять решение о том являются ли изменения в алгоритме в лучшую сторону или нет.
Ссылки по теме
иногда встречаются названия: F-score или мера Ван Ризбергена. ↩
Оценка качества в задачах классификации и регрессии
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
Оценки качества классификации [ править ]
Матрица ошибок (англ. Сonfusion matrix) [ править ]
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок). Допустим, что у нас есть два класса [math]y = \< 0, 1 \>[/math] и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика ( [math]y = 1 [/math] ) можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
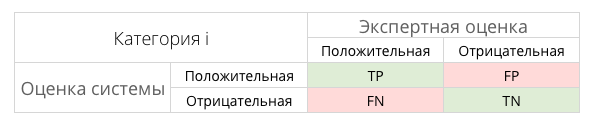
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
| [math]y = 1[/math] | [math]y = 0[/math] | |
| [math]a ( x ) = 1[/math] | Истинно-положительный (True Positive — TP) | Ложно-положительный (False Positive — FP) |
| [math]a ( x ) = 0[/math] | Ложно-отрицательный (False Negative — FN) | Истинно-отрицательный (True Negative — TN) |
Здесь [math]a ( x )[/math] — это ответ алгоритма на объекте, а [math]y [/math] — истинная метка класса на этом объекте. Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP). P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
Аккуратность (англ. Accuracy) [ править ]
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5). Тогда accuracy:
[math] accuracy = \dfrac<5+90> <5+90+10+5>= 86,4 [/math]
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
[math] accuracy = \dfrac<0+100> <0+100+0+10>= 90,9 [/math]
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Точность (англ. Precision) [ править ]
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
[math] Precision = \dfrac
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall) [ править ]
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
[math] Recall = \dfrac
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
F-мера (англ. F-score) [ править ]
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок. Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где [math]β[/math] принимает значения в диапазоне [math]0\lt β\lt 1[/math] если вы хотите отдать приоритет точности, а при [math]β\gt 1[/math] приоритет отдается полноте. При [math]β=1[/math] формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют [math]F_1[/math] ).
Немного о Precision и Recall
FRD и нефункциональные требования
Зачастую в практике системного аналитика, составляющего FRD, встречаются вещи неформализуемые. Примером могут быть требования типа:
Такие требования, будучи записанными в FRD «как есть», являются чудовищным источником проблем впоследствии. Формализация таких требований — постоянная головная боль аналитика. Обычно аналитик решает задачу в два приема: сначала выдвигается «эквивалентное» формальное требование, затем в процессе общения (с заказчиком, экспертом предметной области и т.п.) доказывается, что такое формальное требование может заменить собой исходное требование. Вообще говоря, полученное нами требование не является функциональным; оно описывает не «что» должна уметь делать система, а «как делать». При этом «как делать» должно быть сформулировано с конкретной качественной характеристикой.
Это была преамбула к тезису о том, что системный аналитик должен хорошо владеть математическим аппаратом и заодно уметь объяснять «математику» заказчику. А теперь рассмотрим пример.
О задаче классификации
Предположим, что мы пишем FRD для системы контекстной рекламы, похожей на Amazon Omakase. Одним из модулей нашей будущей системы будет контекстный анализатор:
Анализатор принимает на входе текст веб-страницы и производит его контекстный анализ. То, каким образом он это делает, нас особо не интересует; важно, что на выходе мы получаем набор товарных категорий (множество которых заранее определено). Далее на основе этих категорий мы можем показывать баннеры, товарные ссылки (как Amazon) и т.п. Анализатор для нас пока является черным ящиком, которому мы можем задать вопрос (в виде текста документа) и получить ответ.
Заказчик хочет, чтобы анализатор «хорошо определял контекст». Нам надо сформулировать, что это требование означает. Для начала поговорим о контексте как таковом, т.е. о том самом наборе категорий, который возвращается анализатором. Можно определить это как задачу классификации, когда документу (веб-странице) сопоставляется множество классов из заранее определенного числа; в нашем случае классы — это товарные категории. Задача классификации довольно часто встречается в обработке текстов (например, спам-фильтры).
Метрики оценки
Рассмотрим метрики оценки, применимые к задаче классификации. Допустим, что мы знаем правильные категории для некоторого числа документов. Сгруппируем ответы нашего гипотетического анализатора следующим образом:
Назовем тестовой выборкой множество документов (веб-страниц), для которых мы знаем правильные ответы. Если подсчитать по каждой категории число попаданий (считаем попадания по парам документ — категория), получим каноническую табличку распределения ответов:
| Ожидалось | ||
|---|---|---|
| Получили | tp (true positive) | fp (false positive) |
| fn (false negative) | tn (true negative) | |
Левая колонка таблицы — это «правильные» сочетания документов и категорий (присутствия которых мы ожидаем на выходе), правая — неправильные. Верхняя строка таблицы — положительные (positive) ответы классификатора, нижняя — отрицательные (в нашем случае — отсутствие категории в ответе). Если число всех пар документ — категория равно N, то нетрудно увидеть, что
| Таблица распределения (contingency matrix) дает несколько иной взгляд на оценку качества нашего классификатора, нежели просто подсчет правильных и неправильных ответов. Здесь обозначено целых 4 непересекающихся класса ответов, множества которых можно изобразить на картинке. Здесь зеленые области обозначают правильные ответы, красные — неправильные. Весь прямоугольник целиком соответствует нашей выборке из N пар. | 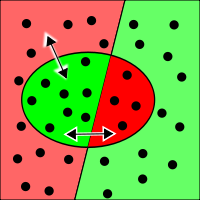 |
В общем-то, теперь можно записать требование заказчика в виде 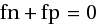
В числителе мы видим диагональ матрицы — суммарное число правильных ответов, который делится на общее число вопросов. Например, анализатор, давший 9 правильных ответов из 10 возможных, имеет accuracy 90%.
Метрика F1
Простым примером неприменимости accuracy-метрики является задача определения обувного бренда. Допустим, мы хотим подсчитать число упоминаний обувных брендов в тексте. Рассмотрим задачу классификации, целью которой будет определить, является ли указанная сущность обувным брендом (Timberland, Columbia, Ted Baker, Ralph Lauren и т.п.). Иначе говоря, мы разбиваем сущности в тексте на два класса: A — Обувной бренд, B — Все остальное.
Теперь рассмотрим вырожденный классификатор, который просто возвращает класс B (Все остальное) для любых сущностей. Для этого классификатора число истинно-положительных ответов будет равно 0. Вообще говоря, давайте подумаем на тему, а часто ли при чтении текста в интернете нам встречаются обувные бренды? Оказывается, как ни странно, что в общем случае 99.9999% слов текста не являются обувными брендами. Построим матрицу распределения ответов для выборки в 100.000:
| Ожидалось | ||
|---|---|---|
| Получили | tp = 0 | fp = 0 |
| fn = 10 | tn = 99990 | |
Вычислим его accuracy, который будет равен 99990 / 100000 = 99.99%! Итак, мы легко построили классификатор, который по сути не делает ничего, однако имеет огромный процент правильных ответов. В то же время совершенно понятно, что задачу определения обувного бренда мы не решили. Дело в том, что правильные сущности в нашем тексте сильно «разбавлены» другими словами, которые для классификации никакого значения не имеют. Учитывая этот пример, вполне понятно желание использовать другие метрики. Например, значение tn явно является «мусорным» — оно вроде как означает правильный ответ, но разрастание tn в итоге сильно «подавляет» вклад tp (который нам важен) в формулу accuracy.
Определим меру точности (P, precision) как:
Как нетрудно заметить, мера точности характеризует, сколько полученных от классификатора положительных ответов являются правильными. Чем больше точность, тем меньше число ложных попаданий.
Мера точности, однако, не дает представление о том, все ли правильные ответы вернул классификатор. Для этого существует так называемая мера полноты (R, recall):
Мера полноты характеризует способность классификатора «угадывать» как можно большее число положительных ответов из ожидаемых. Заметим, что ложно-положительные ответы никак не влияют на эту метрику.
Precision и Recall дают довольно исчерпывающую характеристику классификатора, причем «с разных углов». Обычно при построении подобного рода систем приходится все время балансировать между двумя этими метриками. Если вы пытаетесь повысить Recall, делая классификатор более «оптимистичным», это приводит к падению Precision из-за увеличения числа ложно-положительных ответов. Если же вы подкручиваете свой классификатор, делая его более «пессимистичным», например, строже фильтруя результаты, то при росте Precision это вызовет одновременное падение Recall из-за отбраковки какого-то числа правильных ответов. Поэтому удобно для характеристики классификатора использовать одну величину, так называемую метрику F1:
Фактически это просто среднее гармоническое величин P и R. Метрика F1 достигает своего максимума 1 (100%), если P = R = 100%.
(нетрудно прикинуть, что для нашего вырожденного классификатора F1 = 0). Величина F1 является одной из самых распространенных метрик для подобного рода систем. Именно F1 мы и будем использовать, чтобы сформулировать пороговое качество нашего анализатора в FRD.
В вычислении F1 для задачи классификации есть два основных подхода.
Зачем нужен второй способ? Дело в том, что размеры выборки для разных классов могут сильно различаться. Для каких-то классов у нас может быть очень мало примеров, а для каких-то — много. В итоге метрики одного «большого» класса, будучи сведенными в одну общую таблицу, будут «забивать» все остальные. В ситуации, когда мы хотим оценить качество работы системы более-менее равномерно для всех классов, второй вариант подходит лучше.
Обучающая и тестовая выборка
Выше мы рассматривали классификацию на единой выборке, для которой нам известны все ответы. Если применить это к контекстному анализатору, который мы пытаемся описать, все выглядит немного сложнее.
Прежде всего, мы должны зафиксировать товарные категории. Ситуация, когда мы гарантируем какую-то величину F1, а набор классов при этом может неограниченно расширяться, практически тупиковая. Поэтому дополнительно оговаривается, что набор категорий фиксирован.
Мы вычисляем значение F1 по заданной выборке, которая известна заранее. Эта выборка обычно называется обучающей. Однако мы не знаем, как поведет себя классификатор на тех данных, которые нам неизвестны. Для этих целей обычно используется так называемая тестовая выборка, иногда называемая golden set. Разница между обучающей и тестовой выборкой чисто умозрительная: ведь имея некоторое множество примеров, мы можем разрезать его на обучающую и тестовую выборку как нам угодно. Но для самообучающихся систем формирование правильной обучающей выборки очень критично. Неправильно подобранные примеры могут сильно повлиять на качество работы системы.
Типична ситуация, когда классификатор показывает хороший результат на обучающей выборке и совершенно провальный — на тестовой выборке. Если наш алгоритм классификации основан на машинном обучении (т.е. зависит от обучающей выборки), мы можем оценить его качество по более сложной «плавающей» схеме. Для этого все имеющиеся у нас примеры делим, скажем, на 10 частей. Изымаем первую часть и используем ее для обучения алгоритма; оставшиеся 90% примеров используем как тестовую выборку и вычисляем значение F1. Затем изымаем вторую часть и используем в качестве обучающей; получаем другое значение F1, и т.д. В итоге мы получили 10 значений F1, теперь берем их среднее арифметическое значение, которое и станет окончательным результатом. Повторюсь, что это способ (называемый также cross-fold validation) имеет смысл только для алгоритмов, основанных на машинном обучении.
Возвращаясь к написанию FRD, замечаем, что у нас ситуация куда хуже. Мы имеем потенциально неограниченный набор входных данных (все веб-страницы интернета) и нет никакого способа оценить контекст страницы, кроме как участие человека. Таким образом, наша выборка может быть сформирована только вручную, причем сильно зависеть от капризов составителя (а решение о том, отнести ли страницу к какой-то категории, принимает человек). Мы можем оценить меру F1 на известных нам примерах, но никак не можем узнать F1 для всех страниц интернета. Поэтому для потенциально неограниченных наборах данных (таких, как веб-страницы, коих неисчислимо много), иногда используют «метод тыка» (unsupervised). Для этого случайным образом выбирают определенное число примеров (страниц) и по ним оператор (человек) составляет правильный набор категорий (классов). Затем мы можем испытать классификатор на этих выбранных примерах. Далее, считая, что выбранные нами примеры являются типичными, мы можем приближенно оценить точность алгоритма (Precision). При этом Recall мы оценить не можем (неизвестно, сколько правильных ответов находятся за пределами выбранных нами примеров), следовательно, не можем вычислить и F1.
Таким образом, если мы хотим узнать, как ведет себя алгоритм на всех возможных входных данных, самое лучшее, что сможем оценить в этой ситуации — это приближенное значение Precision. Если же все согласны использовать заранее определенную фиксированную выборку, то можно вычислить средние значение F1 по этой выборке.
В итоге?
А в итоге нам придется сделать следующее:
Как видим, написать FRD на такую систему нелегко (особенно последний пункт), но возможно. Что касается порогового значения F1, в таких случаях можно отталкиваться от значений F1 для похожих задач классификации.
Пост был опубликован: Среда, Июнь 6th, 2012 в 6:14 пп