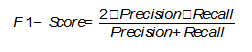f1 score машинное обучение
Основные метрики задач классификации в машинном обучении
Абрамов Роман,
Data Scientist
В каждой задаче машинного обучения ставится вопрос оценки результатов моделей.
Без введенных критериев, невозможно будет ни оценить “успешность” модели, ни сравнить между собой два различных алгоритма. Именно поэтому важно учесть правильный выбор метрик для поставленной задачи, хотя множество существующих метрик может запутать и, в конечном счете, привести к неоптимальному решению.
Несмотря на популярность машинного обучения, во многих её сферах до сих пор не сформировалась единая теоретическая концепция. Исключением не стала и рассматриваемая область. Хоть и существуют некоторые общие рекомендации к применению метрик для некоторых задач, конечное решение лежит на плечах аналитика.
Бинарная классификация
Возьмём к примеру задачу выявления подозрения на определенное заболевание. Если у пациента оно есть, то это будет положительным классом. Если нет – отрицательным. Результатом работы модели может быть определение – следует ли «заподозрить» у пациента какой-то определенный диагноз (тогда результат = true) или нет (тогда результат = false).
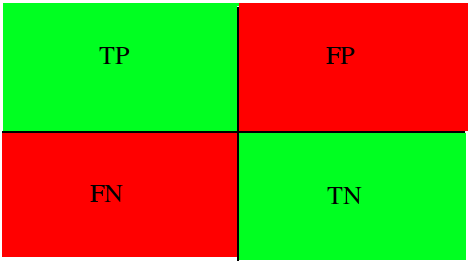
Пусть какой-то набор медицинских данных характерен для данного диагноза. Если наша модель верно определила и поставила положительный класс, тогда это истинно положительный исход, если же модель ставит отрицательную метку класса, тогда это ложно отрицательный исход. В случае отсутствия диагноза у рассматриваемого набора данных исходы модели остаются аналогичными. Тогда если модель относит запись к классу положительную, то мы говорим о ложно положительном исходе (модель «сказала» что диагноз есть, но на самом деле его нет), и наоборот, если модель определят запись как отрицательный класс, то это — истинно отрицательный исход.
Рисунок 1: Матрица сопряженности возможных результатов бинарной классификации
Accuracy
Одной из наиболее простых, а поэтому и распространенной метрикой является точность. Она показывает количество правильно проставленных меток класса (истинно положительных и истинно отрицательных) от общего количества данных и считается следующим образом [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
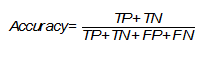
Однако, эта простота является также и причиной, почему её часто критикуют и почему она может абсолютно не подойти под решаемую задачу. Она не учитывает соотношения ложных срабатываний модели, что может быть критическим, особенно в медицинской сфере, когда стоит задача распознать все истинные случаи диагноза.
Вернемся к примеру с подозрением на заболевание. Если наша точность равна 80%, то можно сказать, что в среднем из 100 человек она правильно определит наличие или отсутствие диагноза лишь у 80 человек, тогда как ещё 20 будут либо ложно отрицательными, либо ложно положительными.
Стоит обратить внимание на то, что в некоторых задачах необходимо определить всех пациентов с диагнозом и можно даже пренебречь ложно положительными исходами, так как они могут отсеяться на следующих стадиях исследования (например, после контрольной сдачи анализов), тогда необходимо добавить к этой метрике ещё одну, которая могла бы оценить требуемый приоритет.
Precision
Несмотря на различные английские названия и разные формулы подсчета, русский перевод этой метрики также закрепился как «точность», что может вызвать недоумение и конфуз, поэтому следует уточнять, о чем именно вы говорите. Эта точность показывает количество истинно положительных исходов из всего набора положительных меток и считается по следующей формуле [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
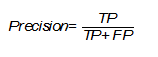
Важность этой метрики определяется тем, насколько высока для рассматриваемой задачи «цена» ложно положительного результата. Если, например, стоимость дальнейшей проверки наличия заболевания у пациента высока и мы просто не можем проверить все ложно положительные результаты, то стоит максимизировать данную метрику, ведь при Precision = 50% из 100 положительно определенных больных диагноз будут иметь лишь 50 из них.
Recall (true positive rate)
В русском языке для этого термина используется слово «полнота» или «чувствительность». Эта метрика определяет количество истинно положительных среди всех меток класса, которые были определены как «положительный» и вычисляется по следующей формуле [The relationship between Precision-Recall and ROC curves ].
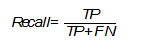
Необходимо уделить особое внимание этой оценке, когда в поставленной задаче ошибка нераспознания положительного класса высока, например, при выставлении диагноза какой-либо смертельной болезни.
F1-Score
В том случае, если Precision и Recall являются одинаково значимыми, можно использовать их среднее гармоническое для получения оценки результатов [On extending f-measure and g-mean metrics to multi-class problems]:
Помимо точечных оценок, существует целый ряд графических методов, способных оценить качество классификации.
ROC (receiver operating characteristic) – график, показывающий зависимость верно классифицируемых объектов положительного класса от ложно положительно классифицируемых объектов негативного класса. Иными словами, соотношение True Positive Rate (Recall) и False Positive Rate (Рисунок 2). При этом, False Positive Rate (FPR) рассчитывается по следующей формуле [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
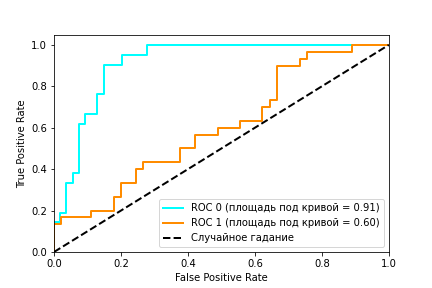
Рисунок 2: ROC кривая
Рисунок 2 содержит пример двух ROC – кривых. Идеальное значение графика находится в верхней левой точке (TPR = 1, a FPR = 0). При этом, кривая, соответствующая FPR = TPR является случайным гаданием, а если график кривой модели или точка находятся ниже этого минимума, то это говорит лишь о том, что лучше подбрасывать монетку, чем использовать эту модель. При этом говорят, что кривая X доминирует над другой кривой Y, если X в любом точке находится левее и выше Y [Using AUC and accuracy in evaluating learning algorithms ], что означает превосходство первого классификатора над вторым.
С помощью ROC — кривой, можно сравнить модели, а также их параметры для поиска наиболее оптимальной (с точки зрения tpr и fpr) комбинации. В этом случае ищется компромисс между количеством больных, метка которых была правильно определена как положительная и количеством больных, метка которых была неправильно определена как положительная.
AUC (Area Under Curve)
В качестве численной оценки ROC кривой принято брать площадь под этой кривой, которая является неплохим «итогом» для кривой. Если между кривыми X и Y существует доминирование первой над второй, то AUC (X) > AUC (Y), обратное не всегда верно. Но AUC обладает так же и статистическим смыслом: она показывает вероятность того, что случайно выбранный экземпляр негативного класса будет иметь меньше вероятность быть распознанным как позитивный класс, чем случайно выбранный позитивный класс [Using AUC and accuracy in evaluating learning algorithms].
Рисунок 3.Два классификатора имеют одинаковую точность, но разный AUC
Мульти-классификация
Все рассмотренные выше метрики относились лишь к бинарной задаче, но, зачастую, классов больше, чем два. Это обуславливает необходимость в обобщении рассмотренных метрик. Одним из возможных способов является вычисление среднего метрики по всем классам [On extending f-measure and g-mean metrics to multi-class problems]. Тогда в качестве «положительного» класса берется вычисляемый, а все остальные — в качестве «отрицательного».
В этом случае формулы для метрик будут выглядеть следующим образом:
Применение в предиктивной аналитике для здравоохранения
Изученную теорию всегда следует подкрепить практикой. В данном случае, можно рассмотреть применение тех или иных метрик для реальных задач, связанных с использованием моделей машинного обучения в здравоохранении. В большинстве случаев рекомендуется использовать метрики AUC и F-Score, потому что они включают в себя широкий список возможных исходов и, как было замечено ранее, AUC превосходит метрику Accuracy, но спор насчет этого ведётся до сих пор.
Основной задачей предиктивной аналитики для здравоохранения является предсказание различных событий. Эта тема довольно неплохо изучена для различных заболеваний и сценариев использования, поэтому существует множество возможных методов её решения. Данный тип задач оценивается всеми рассмотренными метриками для классификации, но чаще остальных можно заметить Accuracy благодаря её простоте. Например, в Disease prediction by machine learning over big data from healthcare communities авторы анализируют медицинские записи с целью предсказания возможности появления какого-либо заболевания и у них получается это на уровне 70% для Accuracy, Precision, Recall и F1. В Intelligent heart disease prediction system using data mining techniques и Heart disease prediction system using naive Bayes метрика Accuracy достигает приблизительно 90-95%, но на это сказывается размер набора данных, который был использован для исследования.
Среди всего списка заболеваний особую актуальность имеют сердечно сосудистые заболевания (ССЗ). Множество исследований, посвященных предсказанию ССЗ демонстрируют то, чего можно достичь в этой области благодаря машинному обучению. Зачастую здесь используется метрика AUC для сравнения качества моделей. Например в A data-driven approach to predicting diabetes and cardiovascular disease with machine learning авторы работали с базой, которая собиралась в течение 20 лет, содержащей более ста признаков. Целью являлось предсказание ранних стадий ССЗ, предиабета и диабета, они добились показателей равных 0.957, 0.802 и 0.839 площади под кривой. В Development and verification of prediction models for preventing cardiovascular diseases авторы исследовали возможность различных исходов (смерть, госпитализация и другие), связанных с ССЗ. Наилучший показатель AUC был равен 0.96. В Перспективы использования методов машинного обучения для предсказания сердечно-сосудистых заболеваний исследуется возможность предсказания ССЗ с помощью методов машинного обучения и некоторых медицинских данных. Для Accuracy, Precision, Recall и AUC были получены результаты 78%, 0.79, 0.67 и 0.84 соответственно.
Заключение
Рассмотренные метрики являются лишь основными и только для задачи классификации. Существует ещё множество различных областей, в которых они будут разными, потому что каждая задача имеют свою специфику и приоритеты. Невозможно дать каких-то четких гарантий и определить, какая из метрик лучше, выбирать и отдавать предпочтение стоит лишь исходя из опыта своего и других исследователей.
Оценка качества в задачах классификации и регрессии
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
Оценки качества классификации [ править ]
Матрица ошибок (англ. Сonfusion matrix) [ править ]
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок). Допустим, что у нас есть два класса [math]y = \< 0, 1 \>[/math] и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика ( [math]y = 1 [/math] ) можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
| [math]y = 1[/math] | [math]y = 0[/math] | |
| [math]a ( x ) = 1[/math] | Истинно-положительный (True Positive — TP) | Ложно-положительный (False Positive — FP) |
| [math]a ( x ) = 0[/math] | Ложно-отрицательный (False Negative — FN) | Истинно-отрицательный (True Negative — TN) |
Здесь [math]a ( x )[/math] — это ответ алгоритма на объекте, а [math]y [/math] — истинная метка класса на этом объекте. Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP). P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
Аккуратность (англ. Accuracy) [ править ]
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5). Тогда accuracy:
[math] accuracy = \dfrac<5+90> <5+90+10+5>= 86,4 [/math]
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
[math] accuracy = \dfrac<0+100> <0+100+0+10>= 90,9 [/math]
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Точность (англ. Precision) [ править ]
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
[math] Precision = \dfrac
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall) [ править ]
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
[math] Recall = \dfrac
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
F-мера (англ. F-score) [ править ]
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок. Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где [math]β[/math] принимает значения в диапазоне [math]0\lt β\lt 1[/math] если вы хотите отдать приоритет точности, а при [math]β\gt 1[/math] приоритет отдается полноте. При [math]β=1[/math] формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют [math]F_1[/math] ).
Дата публикации Jul 3, 2019
ВЧасть IизМультиклассические метрики стали прощеЯ объяснил точность и вспомнить, и как рассчитать их длямульти-классклассификатор. В этом посте я объясню еще один популярныйF1-оценка,точнее F1-счетsтак как есть как минимум 3 варианта,Я объясню, почему используются F1-баллы, и как их вычислять в мультиклассе.
Но сначалаБОЛЬШОЙ ЖИР ПРЕДУПРЕЖДЕНИЕ:F1-баллы широко используются в качестве метрики, но часто являются неправильным способом сравнения классификаторов. Вы будете часто замечать их в научных статьях, где исследователи используют более высокий балл F1 в качестве «доказательства», что их модель лучше, чем модель с более низким баллом. Однако, более высокая оценка F1 не обязательно означает лучший классификатор. Используйте с осторожностью, и возьмите баллы F1 с зерном соли! Подробнее об этом позже.
Как вЧасть IЯ начну с простой настройки двоичной классификации. Просто напоминание: вот матрица путаницы, созданная с использованием нашего двоичного классификатора для фотографий собак. Оценки точности и отзыва, которые мы рассчитывали в предыдущей части, составляют 83,3% и 71,4% соответственно.
F1-счет = 2×(точность×вспомнить) / (точность + отзыв)
В приведенном выше примере оценка F1 нашего двоичного классификатора:
F1-балл = 2 × (83,3% × 71,4%) / (83,3% + 71,4%) = 76,9%
Теперь, когда мы знаем, как вычислить F1-оценку для двоичного классификатора, давайте вернемся к нашему мультиклассовому примеру из первой части. Краткое напоминание: у нас есть 3 класса (Cat, Fish, Hen) и соответствующая матрица путаницы для нашего классификатора. :
Теперь мы хотим вычислить счет Ф1. Как мы это делаем?
С помощью приведенной выше формулы мы можем теперь вычислитьв классеF1-оценка. Например, оценка F1 для Cat:
F1-балл (Cat) = 2 × (30,8% × 66,7%) / (30,8% + 66,7%) = 42,1%
И аналогично для Рыбы и Курицы. Теперь у нас есть полные оценки класса F1:
Макро-F1 = (42,1% + 30,8% + 66,7%) / 3 = 46,5%
Аналогичным образом мы также можем вычислитьмакро-усредненная точностьиМакро усредненный отзыв:
Макро-точность = (31% + 67% + 67%) / 3 = 54,7%
Макро-отзыв = (67% + 20% + 67%) / 3 = 51,1%
(20 августа 2019 г. Я только что узнал, что существует более одной метрики макро-F1! Описанный выше макрос-F1 является наиболее часто используемым, но см. Мой постСказка о двух макро-F1)
При усреднении макро-F1 мы давали равные веса каждому классу. Нам не нужно этого делать: всредневзвешенная оценка F1, илиВзвешенный-F1мы взвешиваем балл F1 каждого класса по количеству образцов из этого класса. В нашем случае у нас всего 25 образцов: 6 кошек, 10 рыб и 9 кур. Таким образом, взвешенная оценка F1 рассчитывается следующим образом:
Взвешенная-F1 = (6×42,1% + 10×30,8% + 9×66 7%) / 25 = 46,4%
Точно так же мы можем вычислить взвешенную точность и взвешенное обращение:
Взвешенные точности = (6×30,8% + 10×66,7% + 9×66,7%) / 25 = 58,1%
Взвешенный отзыв = (6×66,7% + 10×20,0% + 9×66,7%) / 25 = 48,0%
Напомним, что это доля истинных позитивов от фактических позитивов (TP / (TP + FN)). ТП как и прежде: 4 + 2 + 6 = 12. Как мы вычисляем количество ложных негативов? Если взять наш предыдущий пример, если образец Cat был предсказан как рыба, этот образец является ложным отрицанием для Cat. В более широком смысле, каждая ошибка предсказания (X неправильно классифицируется как Y) является ложным положительным значением для Y и ложным отрицательным значением для X. Таким образом, общее количество ложных отрицательных значений снова является общим количеством ошибок предсказания (то есть розовых ячеек) и поэтому отзыв такой же, как точность: 48,0%.
Поскольку точность = отзыв в случае микро-усреднения, они также равны их гармоническому среднему значению. Другими словами, в случае микро-F1:
микро-F1знак равномикро-точностьзнак равномикро-отзыв
Кроме того, это также общий классификаторточность:доля правильно классифицированных образцов из всех образцов,Подводя итог, для случая микро-F1 всегда справедливо следующее:
микро-F1знак равномикро-точностьзнак равномикроотзыв = точность
Ранее я упоминал, что баллы F1 следует использовать с осторожностью. Зачем? Хотя они действительно удобны для быстрого сравнения на высоком уровне, их главный недостаток заключается в том, что они придают одинаковый вес точности и отзыву. Как выдающийся статистик Дэвид Хэндобъяснил«Относительная важность, придаваемая точности и отзыву, должна быть аспектом проблемы». Классификация больного как здорового человека отличается от классификации здорового человека как больного, и это должно отражаться в том, как веса и затраты используются для выбора лучшего классификатора для конкретной проблемы, которую вы пытаетесь решить. Это верно для двоичных классификаторов, и проблема усугубляется при вычислении мультиклассовых баллов F1, таких как макро-, взвешенные или микро-F1 баллы. В случае нескольких классов разные ошибки прогнозирования имеют различное значение. Предсказание X как Y, вероятно, будет иметь другую стоимость, чем предсказание Z как W, и так далее. Стандартные оценки F1 не учитывают знания предметной области.
Наконец, давайте еще раз посмотрим на наш скрипт и вывод sk-learn в Python.
Здесь снова вывод скрипта. Две нижние строки показываютмакро-усредненнойа такжевзвешенный усредненныйТочность, отзыв и F1-оценка. Точность (48,0%) также рассчитывается, что равно баллу микро-F1.
На этом завершается краткое введение из двух частей в метрики нескольких классов. Я надеюсь, что вы нашли эти посты полезными.