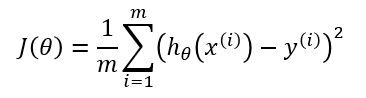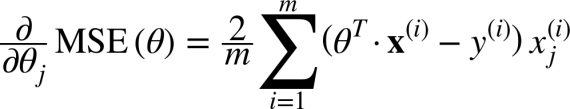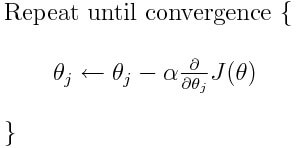градиентный спуск машинное обучение
Математика для искусственных нейронных сетей для новичков, часть 3 — градиентный спуск продолжение
В предыдущей части я начал разбор алгоритма оптимизации под названием градиентный спуск. Предыдущая статья оборвалась на писании варианта алгоритма под названием пакетный градиентный спуск.
Существует и другая версия алгоритма — стохастический градиентный спуск. Стохастический = случайный.
Повторять, пока не сойдется
<
for i in train_set
<
>
>
Также напомню как выглядит пакетный:
Повторять, пока не сойдется
<
>
Формулы похожи, но, как видно, пакетный градиентный спуск вычисляет один шаг, используя сразу весь набор данных, тогда как стохастический за шаг использует только 1 элемент. Можно два этих варианта скрестить, получив мини-пакетный (mini-batch) спуск, который за раз обрабатывает, к примеру, 100 элементов, а не все или один.
Два этих варианта ведут себя похоже, но не одинаково. Пакетный спуск действительно следует в направлении наискорейшего спуска, тогда как стохастический, используя только один элемент из обучающей выборки, не может верно вычислить градиент для всей выборки. Это различие проще пояснить графически. Для этого я модифицирую код из первой части, в котором вычислялись коэффициенты линейной регрессии. Функция стоимости для нее выглядит следующим образом: 
Как видно, это немного вытянутый параболоид. И также его «вид сверху», где крестом отмечен истинный минимум, найденный аналитически. 
Сперва рассмотрим, как ведет себя пакетный спуск:
Из-за того, что параболоид вытянутый, по его «дну» проходит «овраг», в который мы попадаем. Из-за этого последние шаги вдоль этого оврага очень маленькие, но тем не менее рано или поздно градиентный спуск доберется до минимума. Спуск происходит по линии антиградиента, каждый шаг приближаясь к минимуму.
Теперь та же самая функция, но для стохастического спуска:
В определении сказано, что выбирается только один элемент — в этом коде каждый последующий элемент выбирается случайным образом.
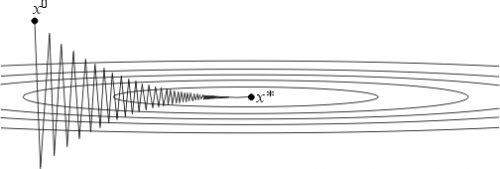
Как видно, в случае стохастического варианта, спуск идет не по линии антиградиента, а вообще непонятно как — каждый шаг отклоняясь в случайную сторону. Может показаться, что такими случайными дергаными движениями к минимуму можно прийти только случайно, однако было доказано, что стохастический градиентный спуск сходится почти наверное. Пару ссылок, например.
На 200 элементах разницы в скорости почти никакой нет, однако, увеличив количество элементов до 2000 (что тоже очень мало) и подкорректировав скорость обучения, стохастический вариант бьет пакетный, как хочет. Однако, в силу стохастической природы, иногда метод промахивается, осциллируя возле минимума без возможности остановиться. Как-то так:
Этот факт делает неприменимой чистую реализацию. Чтобы как-то призвать к порядку и снизить «случайность» можно снизить скорость обучения. На практике применяют mini-batch вариацию — от стохастической она отличается тем, что вместо одного случайно выбранного элемента выбирают больше одного.
О разнице, плюсах и минусах данных двух подходов написано достаточно много, вкратце подведу итог:
— Пакетный спуск хорош для строго выпуклых функций, потому что уверенно стремится к минимуму глобальному или локальному.
— Стохастический в свою очередь лучше работает на функциях с большим количеством локальных минимумов — каждый шаг есть шанс, что очередное значение «выбьет» из локальной ямы и конечное решение будет более оптимальным, нежели для пакетного спуска.
— Стохастический вычисляется быстрее — на каждом шаге нужны не все элементы из выборки. Вся выборка целиком может не влезть в память. Но требуется больше шагов.
— Для стохастического легко добавить новые элементы во время работы («онлайн» обучение).
— В случае mini-batch, можно также векторизовать код, что значительно ускорит его выполнение.
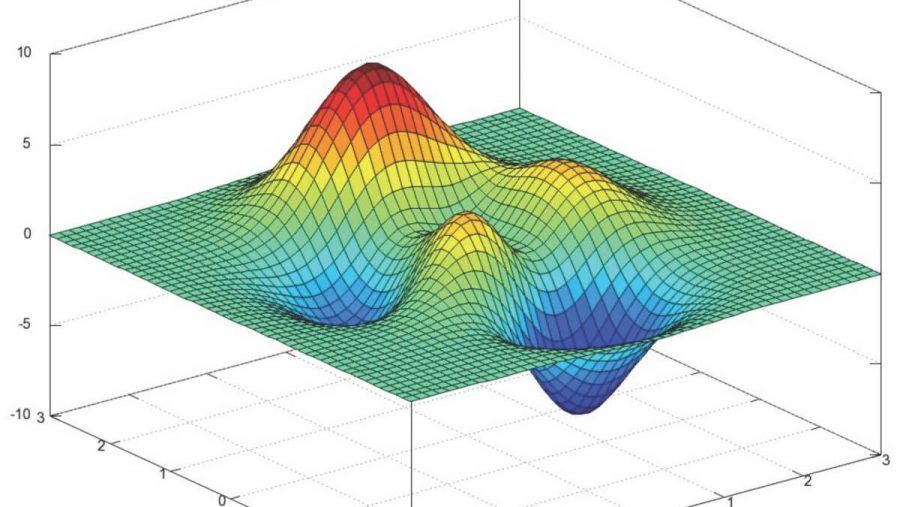
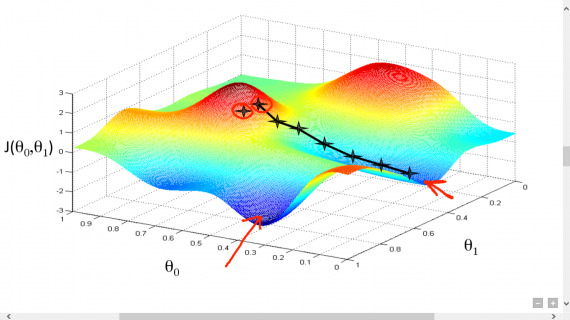
Также у градиентного спуска существует множество модификаций — momentum, наискорейшего спуска, усреднение, Adagrad, AdaDelta, RMSProp и другие. Здесь можно посмотреть короткий обзор некоторых. Частенько они используют значения градиента с предыдущих шагов или автоматически вычисляют наилучшее значение скорости для данного шага. Использование этих методов для простой гладкой функции МНК не имеет особого смысла, но в случае нейронных сетей и сетей с большим количеством слоев\нейронов, функция стоимости становится совсем грустной и градиентный спуск может застрять в локальной яме, так и не достигнув оптимального решения. Для таких проблем подходят методы на стероидах. Вот пример функции простой для минимизации (двумерная линейная регрессия с МНК): 
И пример нелинейной функции:
Градиентный спуск — метод оптимизации первого порядка (первая производная). Также существует много методов второго порядка — для них необходимо вычислять вторую производную и строить гессиан (довольно затратная операция — 
На голых циклах далеко не уедешь — код нуждается в векторизации. Основной алгоритм для векторизации — пакетный градиентный спуск, с оговоркой, что 
Для доказательства, пройдем пару шагов в обратную сторону:
В предыдущей формуле, в каждой строке индекс j зафиксирован, а i — изменяется от 1 до n. Свернув сумму:
Это выражение точно такое же, что и в определении градиентного спуска. Наконец, завершающий шаг — сворачивание векторов и матриц:
Стоимость одного такого шага — 

Обратите внимание, что поменялись местами предсказанное значение и реальное, что привело к изменению знака перед скоростью обучения.
Градиентный спуск: всё, что нужно знать
Градиентный спуск — самый используемый алгоритм обучения, он применяется почти в каждой модели машинного обучения. Градиентный спуск — это, по сути, и есть то, как обучаются модели. Без ГС машинное обучение не было бы там, где сейчас. Метод градиентного спуска с некоторой модификацией широко используется для обучения персептрона и глубоких нейронных сетей, и известен как метод обратного распространения ошибки.
В этом посте вы найдете объяснение градиентного спуска с небольшим количеством математики. Краткое содержание:
Что такое градиентный спуск
Градиентный спуск — метод нахождения минимального значения функции потерь (существует множество видов этой функции). Минимизация любой функции означает поиск самой глубокой впадины в этой функции. Имейте в виду, что функция используется, чтобы контролировать ошибку в прогнозах модели машинного обучения. Поиск минимума означает получение наименьшей возможной ошибки или повышение точности модели. Мы увеличиваем точность, перебирая набор учебных данных при настройке параметров нашей модели (весов и смещений).
Итак, градиентный спуск нужен для минимизации функции потерь.
Суть алгоритма – процесс получения наименьшего значения ошибки. Аналогично это можно рассматривать как спуск во впадину в попытке найти золото на дне ущелья (самое низкое значение ошибки).
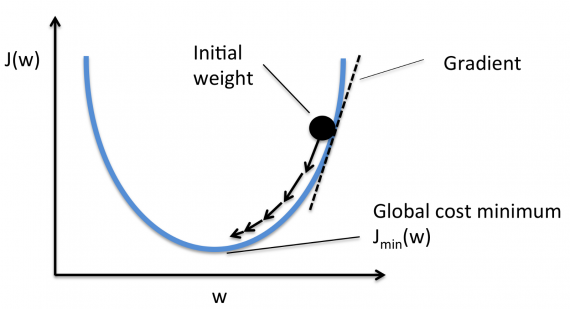
В дальнейшем, чтобы найти самую низкую ошибку (глубочайшую впадину) в функции потерь (по отношению к одному весу), нужно настроить параметры модели. Как мы их настраиваем? В этом поможет математический анализ. Благодаря анализу мы знаем, что наклон графика функции – производная от функции по переменной. Это наклон всегда указывает на ближайшую впадину!
На рисунке мы видим график функции потерь (названный «Ошибка» с символом «J») с одним весом. Теперь, если мы вычислим наклон (обозначим это dJ/dw) функции потерь относительно одного веса, то получим направление, в котором нужно двигаться, чтобы достичь локальных минимумов. Давайте пока представим, что наша модель имеет только один вес.
Важно: когда мы перебираем все учебные данные, мы продолжаем добавлять значения dJ/dw для каждого веса. Так как потери зависят от примера обучения, dJ/dw также продолжает меняться. Затем делим собранные значения на количество примеров обучения для получения среднего. Потом мы используем это среднее значение (каждого веса) для настройки каждого веса.
Также обратите внимание: Функция потерь предназначена для отслеживания ошибки с каждым примером обучениям, в то время как производная функции относительного одного веса – это то, куда нужно сместить вес, чтобы минимизировать ее для этого примера обучения. Вы можете создавать модели даже без применения функции потерь. Но вам придется использовать производную относительно каждого веса (dJ/dw).
Теперь, когда мы определили направление, в котором нужно подтолкнуть вес, нам нужно понять, как это сделать. Тут мы используем коэффициент скорости обучения, его называют гипер-параметром. Гипер-параметр – значение, требуемое вашей моделью, о котором мы действительно имеем очень смутное представление. Обычно эти значения могут быть изучены методом проб и ошибок. Здесь не так: одно подходит для всех гипер-параметров. Коэффициент скорости обучения можно рассматривать как «шаг в правильном направлении», где направление происходит от dJ/dw.
Это была функция потерь построенная на один вес. В реальной модели мы делаем всё перечисленное выше для всех весов, перебирая все примеры обучения. Даже в относительно небольшой модели машинного обучения у вас будет более чем 1 или 2 веса. Это затрудняет визуализацию, поскольку график будет обладать размерами, которые разум не может себе представить.
Подробнее о градиентах
Кроме функции потерь градиентный спуск также требует градиент, который является dJ/dw (производная функции потерь относительно одного веса, выполненная для всех весов). dJ/dw зависит от вашего выбора функции потерь. Наиболее распространена функция потерь среднеквадратичной ошибки.
Производная этой функции относительно любого веса (эта формула показывает вычисление градиента для линейной регрессии):
Это – вся математика в ГС. Глядя на это можно сказать, что по сути, ГС не содержит много математики. Единственная математика, которую он содержит в себе – умножение и деление, до которых мы доберемся. Это означает, что ваш выбор функции повлияет на вычисление градиента каждого веса.
Коэффициент скорости обучения
Всё, о чём написано выше, есть в учебнике. Вы можете открыть любую книгу о градиентном спуске, там будет написано то же самое. Формулы градиентов для каждой функции потерь можно найти в интернете, не зная как вывести их самостоятельно.
Однако проблема у большинства моделей возникает с коэффициентом скорости обучения. Давайте взглянем на обновленное выражение для каждого веса (j лежит в диапазоне от 0 до количества весов, а Theta-j это j-й вес в векторе весов, k лежит в диапазоне от 0 до количества смещений, где B-k — это k-е смещение в векторе смещений). Здесь alpha – коэффициент скорости обучения. Из этого можно сказать, что мы вычисляем dJ/dTheta-j ( градиент веса Theta-j), и затем шаг размера alpha в этом направлении. Следовательно, мы спускаемся по градиенту. Чтобы обновить смещение, замените Theta-j на B-k.
Если этот размера шага alpha слишком велик, мы преодолеем минимум: то есть промахнемся мимо минимума. Если alpha слишком мала, мы используем слишком много итераций, чтобы добраться до минимума. Итак, alpha должна быть подходящей.
Использование градиентного спуска
Что ж, вот и всё. Это всё, что нужно знать про градиентный спуск. Давайте подытожим всё в псевдокоде.
Примечание: Весы здесь представлены в векторах. В более крупных моделях они, наверное, будут матрицами.
От i = 0 до «количество примеров обучения»
1. Вычислите градиент функции потерь для i-го примера обучения по каждому весу и смещению. Теперь у вас есть вектор, который полон градиентами для каждого веса и переменной, содержащей градиент смещения.
2. Добавьте градиенты весов, вычисленные для отдельного аккумулятивного вектора, который после того, как вы выполнили итерацию по каждому учебному примеру, должен содержать сумму градиентов каждого веса за несколько итераций.
3. Подобно ситуации с весами, добавьте градиент смещения к аккумулятивной переменной.
Теперь, ПОСЛЕ перебирания всех примеров обучения, выполните следующие действия:
1. Поделите аккумулятивные переменные весов и смещения на количество примеров обучения. Это даст нам средние градиенты для всех весов и средний градиент для смещения. Будем называть их обновленными аккумуляторами (ОА).
2. Затем, используя приведенную ниже формулу, обновите все веса и смещение. Вместо dJ / dTheta-j вы будете подставлять ОА (обновленный аккумулятор) для весов и ОА для смещения. Проделайте то же самое для смещения.
Это была только одна итерация градиентного спуска.
Повторите этот процесс от начала до конца для некоторого количества итераций. Это означает, что для 1-й итерации ГС вы перебираете все примеры обучения, вычисляете градиенты, потом обновляете веса и смещения. Затем вы проделываете это для некоторого количества итераций ГС.
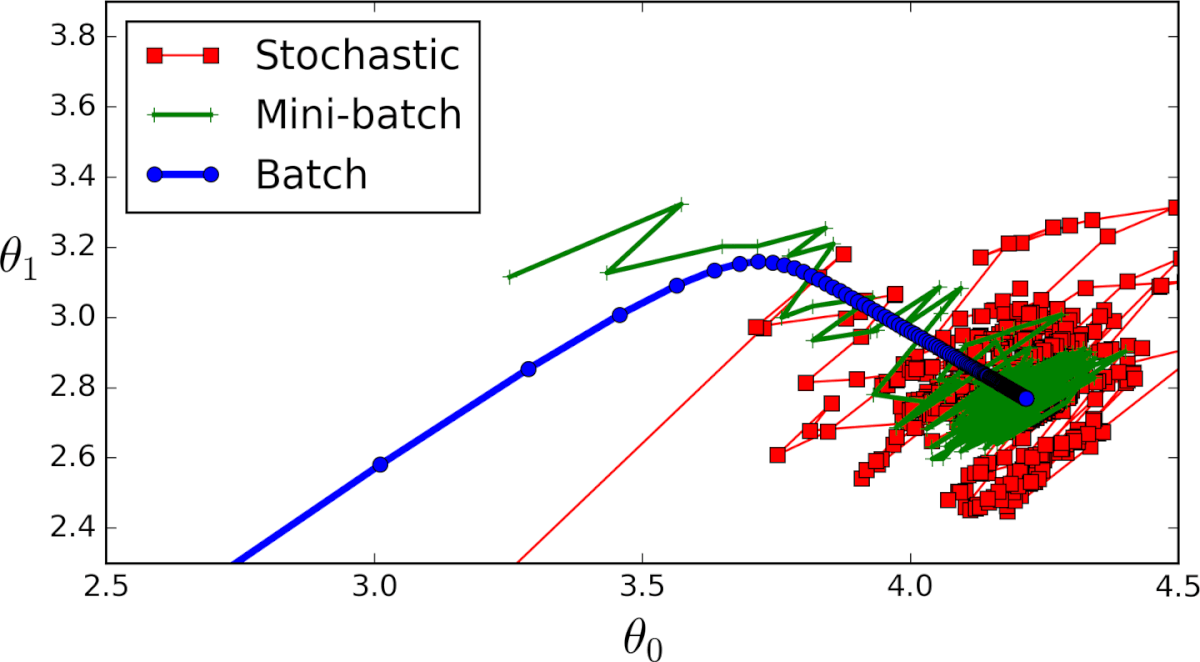
Различные типы градиентного спуска
Существует 3 варианта градиентного спуска:
1. Мini-batch: тут вместо перебирания всех примеров обучения и с каждой итерацией, выполняющей вычисления только на одном примере обучения, мы обрабатываем n учебных примеров сразу. Этот выбор хорош для очень больших наборов данных.
2. Стохастический градиентный спуск: в этом случае вместо использования и зацикливания на каждом примере обучения, мы ПРОСТО ИСПОЛЬЗУЕМ ОДИН РАЗ. Есть несколько вещей замечаний:
3. Серия ГС: это то, о чем написано в предыдущих разделах. Цикл на каждом примере обучения.
Пример кода на python
Применимо к cерии ГС, так будет выглядеть блок учебного кода на Python.
Вот и всё. Теперь вы должны хорошо понимать, что такое метод градиентного спуска.
Метод градиентного спуска
Материал из MachineLearning.
Содержание
Введение
Пусть функция такова, что можно вычислить ее градиент. Тогда можно применить метод градиентного спуска, описанный в данной статье.
В статье приведены теоремы сходимости метода градиентного спуска, а также рассмотрена его варианты:
Метод градиентного спуска
Идея метода
Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом :
Алгоритм
Выход: найденная точка оптимума
Критерий останова
Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:
Сходимость градиентного спуска с постоянным шагом
Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.
Тогда при любом выборе начального приближения.
В условиях теоремы градиентный метод обеспечивает сходимость либо к точной нижней грани (если функция не имеет минимума) либо к значению Существуют примеры, когда в точке реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.
Определение. Дифференцируемая функция называется сильно выпуклой (с константой 0″ alt= «\Lambda>0» />), если для любых и из справедливо
Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.
Тогда при любом выборе начального приближения.
Выбор оптимального шага
При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной:
Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Далее будут описаны два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.
Градиентный метод с дроблением шага
В этом варианте градиентного метода величина шага на каждой итерации выбирается из условия выполнения неравенства
где — некоторая заранее выбранная константа.
Метод наискорейшего спуска
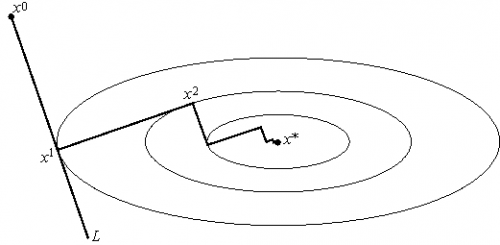
Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче :
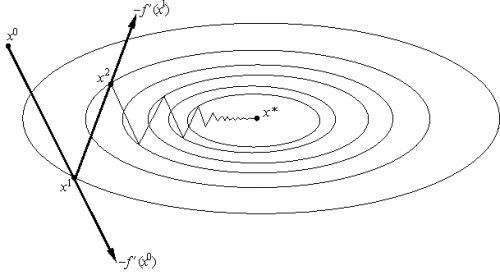
Другими словами, выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.
Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.
В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.
Числовые примеры
Метод градиентного спуска с постоянным шагом
Для исследования сходимости метода градиентного спуска с постоянным шагом была выбрана функция:
Результаты эксперимента отражены в таблице:
| Значение шага | Достигнутая точность | Количество итераций |
|---|---|---|
| 0.1 | метод расходится | |
| 0.01 | 2e-4 | 320 |
| 0.001 | 2e-3 | 2648 |
| 0.0001 | 1e-2 | 20734 |
Из полученных результатов можно сделать вывод, что при слишком большом чаге метод расходится, при слишком малом сходится медленно и точчность хуже. Надо выбирать шаг наибольшим из тех, при которых метод сходится.
Градиентный метод с дроблением шага
Для исследования сходимости метода градиентного спуска с дроблением шага (2) была выбрана функция:
Результаты эксперимента отражены в таблице:
| Значение параметра | Значение параметра | Значение параметра | Достигнутая точность | Количество итераций |
|---|---|---|---|---|
| 0.95 | 0.95 | 1 | 5e-4 | 629 |
| 0.1 | 0.95 | 1 | 1e-5 | 41 |
| 0.1 | 0.1 | 1 | 2e-4 | 320 |
| 0.1 | 0.95 | 0.01 | 2e-4 | 320 |
Метод наискорейшего спуска
Для исследования сходимости метода наискорейшего спуска была выбрана функция:
Для решения одномерных задач оптимизации использован метод золотого сечения.
Метод получил точность 6e-8 за 9 итераций.
Отсюда можно сделать вывод, что метод наискорейшего спуска сходится быстрее, чем градиентный метод с дроблением шага и метод градиентного спуска с постоянным шагом.
Недостатком методом наискорейшего спуска явлляется необходимость решать одномерную задачу оптимизации.
Рекомендации программисту
При программировании методов градиентного спуска следует аккуратно относится к выбору параметров, а именно
Заключение
Методы градиентного спуска являются достаточно мощным инструментом решения задач оптимизации. Главным недостатком методов является ограниченная область применимости.
Понимание основ градиентного спуска
Градиентный спуск, пожалуй, является наиболее признанной стратегией оптимизации, используемой в глубоком обучении и машинном обучении. Ученые, занимающиеся данными, часто используют ее, когда есть возможность совместить каждый алгоритм с обучающими моделями. Понимание алгоритма спуска по градиенту относительно простое, а его реализация еще проще. Рассмотрим внутреннюю работу градиентного спуска, его различные типы и преимущества.
Что такое градиентный спуск?
Программисты используют градиентный спуск как алгоритм оптимизации при обучении машинных моделей. Основываясь на выпуклых функциях, градиентное спусковое спускование итеративно корректирует некоторые из своих параметров, чтобы свести к минимуму конкретную функцию.
Специалисты по данным используют градиентный спуск для нахождения значений параметров функции, которые максимально снижают стоимость функций. Они начинают с определения значений начального параметра. В градиентном спуске используется вычисление для итеративной корректировки значений, чтобы минимизировать конкретную функцию затрат. Для полного понимания спуска градиента необходимо знать, что такое градиент.
Понимание градиента
Основная функция градиента заключается в измерении изменений в каждом весе в отношении изменения ошибок. Думайте о градиентах как о наклоне функции. Наклон будет более крутым в зависимости от высоты градиента – это благоприятное условие для моделей, так как они могут быстро учиться. Однако, модель перестанет учиться, если наклон станет нулевым. С математической точки зрения, градиент лучше всего описывать как ограниченную производную относительно его входных данных.
Подумайте о человеке с завязанными глазами, желающем подняться на вершину холма с минимальными усилиями. Скорее всего, он сделает длинные шаги в самом крутом направлении. Однако, шаги этого человека будут становиться меньше, чтобы предотвратить перебор. Вы можете использовать градиент для математического описания этого процесса.
Градиенты, начинающиеся от X0 и заканчивающиеся в X1, значительно длиннее, чем градиенты, начинающиеся от X3 и заканчивающиеся в X4. Почему? Потому что наклон/крутизна холма определяет длину вектора. Это обеспечивает идеальное представление рассмотренной ранее аналогии холма, поскольку он становится менее крутым по мере того, как человек поднимается выше.
Как работает градиентный спуск?
Вместо того, чтобы подниматься на холм, представьте себе спуск по уклону, как спуск на дно долины. Понимание этой аналогии проще, так как это алгоритм минимизации, который уменьшает конкретную функцию. Давайте разберемся в спуске по градиенту с помощью уравнения:
b представляет собой следующую позицию альпиниста
означает его нынешнее положение
минус относится к минимизирующей части спуска градиента
Гамма, расположенная в центре, представляет собой фактор ожидания.
(Δf(a) ) означает самое крутое направление спуска.
Сначала вы можете запутаться в этой формуле, но она более проста, чем вы думаете. Она информирует нас о следующей позиции, по которой мы должны идти: направление спуска.
Почему скорость обучения так важна?
Крайне важно установить скорость обучения на соответствующие значения, чтобы помочь градиентному спуску достичь местных минимумов. Поэтому лучше не устанавливать их слишком высокие или низкие. Это крайне важно, поскольку достижение минимума может осложниться чрезмерно длинными шагами. Поэтому, если мы установим скорость обучения на меньшие значения, то градиентный спуск в конечном итоге может достичь своих локальных минимумов. Однако это может занять некоторое время.
Как обеспечить его функционирование Оптимально
Отличным способом оптимального обеспечения функций спуска по градиенту является организация функции затрат в процессе оптимизации. Введите количество повторений по оси X, а значение функции затрат будет введено по оси Y. Это поможет Вам увидеть значение функции затрат после каждой итерации спуска градиента, а также позволит определить точность обучения. Вы также можете попробовать различные значения и построить их вместе.
Функция стоимости будет уменьшаться после каждой итерации, если спуск градиента функционирует оптимально. Скорость спуска градиента сходится, когда он не может уменьшить функцию затрат, и остается на том же уровне. Количество итераций, необходимых для сходимости градиента, сильно варьируется. Иногда для этого требуется пятьдесят итераций, а в других случаях он может достигать двух-трех миллионов. Это вызывает трудности при предварительной оценке итераций.
Некоторые алгоритмы могут автоматически информировать вас о том, имело ли место схождение при спуске по градиенту. Однако лучше всего заранее установить порог сходимости, который также довольно сложно оценить. Это существенная причина, по которой простые графики лучше всего подходят для тестирования сходимости.
Различные типы градиентного спуска
Вы найдете три хорошо узнаваемых типа спуска с уклоном. Давайте посмотрим на них поближе:
Пакетный градиентный спуск
Также известный как спуск по ванильному градиенту, пакетный спуск по градиенту вычисляет ошибки для каждого примера в обучающем наборе данных. Однако, он делает это только после того, как каждый тренировочный пример проходит тщательную оценку. Справедливо сравнить этот процесс с циклом. Некоторые люди также называют это тренировочной эпохой.
Пакетный спуск по градиенту имеет несколько преимуществ. Его вычислительная эффективность, в частности, чрезвычайно удобна, так как он развивает стабильную конвергенцию и стабильный градиент ошибки. Тем не менее, спуск по пакетному градиенту также имеет некоторые недостатки. Иногда его стабильный градиент ошибки может привести к неблагоприятному состоянию сходимости. Кроме того, ему необходимо наличие обучающего набора данных в алгоритме и памяти.
Стохастический градиент спуска
SGD предоставляет обновления для индивидуальных параметров для каждого учебного примера. Это помогает уделить внимание каждому примеру, гарантируя, что процесс будет безошибочным. В зависимости от проблемы, это может помочь SGD стать более быстрым по сравнению с серийным спуском по градиенту. Регулярные обновления дают нам детальные показатели улучшения.
Тем не менее, эти обновления являются дорогостоящими с вычислительной точки зрения, особенно при сравнении с подходом, используемым при пакетном спуске по градиенту. Более того, частота обновлений может вызывать шумные градиенты и предотвращать снижение частоты ошибок. Вместо этого частота ошибок скачет и становится проблематичной в долгосрочной перспективе.
Мини-пакетный спуск по градиенту
Ученые, занимающиеся сбором данных, используют метод спуска по градиенту в мини-группах. Почему? Потому что это идеальное сочетание концепций стохастического градиентного спуска и пакетного градиентного спуска. Он разделяет наборы данных (обучение) на партии и запускает обновление для каждой партии, создавая баланс между эффективностью BGD и надежностью SCD.
Популярные мини-пакеты варьируются от пятидесяти до двухсот пятидесяти шести, но, как и некоторые другие методы машинного обучения, в них нет четких правил, так как они варьируются от одного приложения к другому. Люди используют его как опцию для тренировки нейронных сетей. Это также популярный тип спуска по градиенту в условиях глубокого обучения.