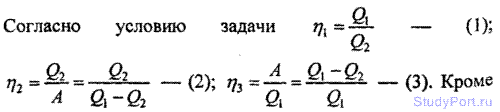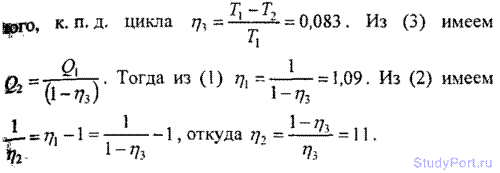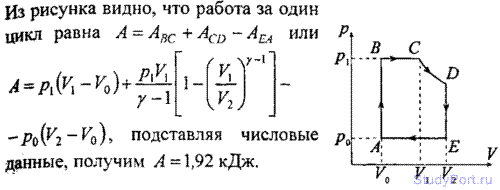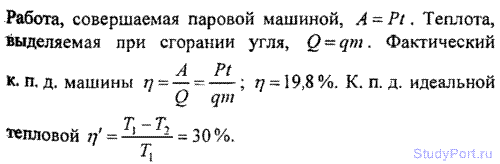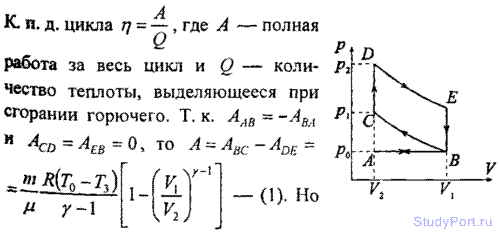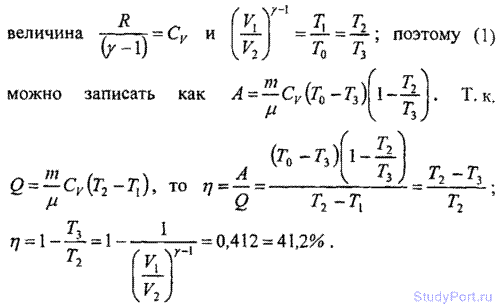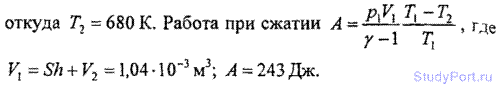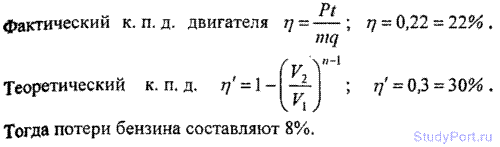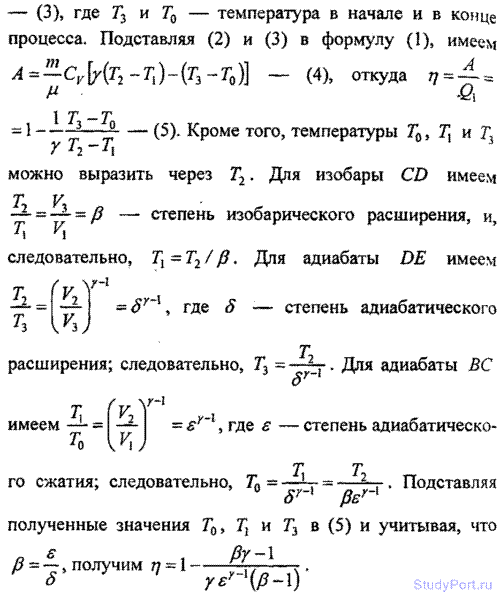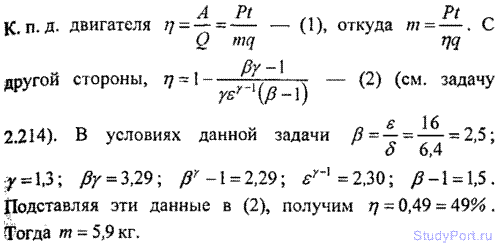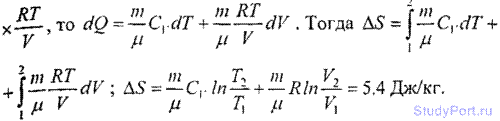Холодильная машина работающая по обратному циклу карно должна поддерживать в своей камере

33. Второе начало термодинамики: задачи по физике с ответами без решений

(Все задачи по молекулярно-кинетической теории и ответы к ним находятся в zip-архиве (290 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)

33.1. У тепловой машины, работающей по циклу Карно, температура нагревателя в n = 1,6 раз больше температуры холодильника. За один цикл машина производит работу A = 12 кДж. Какая работа затрачивается на изотермическое сжатие рабочего вещества? [ A₁ = 20 кДж ]

33.2. В каком случае КПД цикла Карно повысится больше: при увеличении температуры нагревателя на ΔT или при уменьшении температуры холодильника на ту же ΔT? [смотрите ответ в общем файле темы]

33.3. Идеальный одноатомный газ совершает замкнутый процесс (рис.). Определить КПД цикла. [ ≅ 17.4% ]

33.4. Найти КПД тепловой машины, работающей с ν молями одноатомного идеального газа по циклу, состоящему из адиабаты 1 – 2, изотермы 2 – 3 и изохоры 3 – 1 (рис.). Работа, совершенная над газом на участке 2 – 3 равна A, разность максимальной и минимальной температур в цикле равна ΔT. [смотрите ответ в общем файле темы]

33.5. КПД цикла 1 – 2 – 4 – 1 равен η₁, а КПД цикла 2 – 3 – 4 – 2 равен η₂ (рис.). Найти КПД цикла 1 – 2 – 3 – 4 – 1. [ η = η₁ + η₂ − η₁η₂ ]

33.6. Водород совершает цикл Карно. Найти КПД цикла, если при адиабатическом расширении: а) объем газа увеличивается в 2 раза; б) давление уменьшается в 2 раза. [смотрите ответ в общем файле темы]

33.7. Найти КПД цикла, состоящего из двух изобар и двух адиабат, если в пределах цикла давление изменяется в n раз. Показатель адиабаты рабочего вещества равен γ. [смотрите ответ в общем файле темы]

33.8. Холодная машина, работающая по обратному циклу Карно, должна поддерживать в камере температуру t₂ = −10 °С при температуре окружающей среды t₁ = 20 °С. Какую работу надо совершить над рабочим веществом машины, чтобы отвести из камеры машины Q = 140 кДж тепла? [ A = 16 кДж ]

33.9. Тепловую машину, работавшую по циклу Карно с КПД η = 10 %, используют при тех же тепловых резервуарах как холодильную машину. Найти ее холодильный коэффициент. [9]

33.10. Идеальная тепловая машина, работающая по обратному циклу, получает тепло от холодильника с водой при температуре t₁ = 0 °С и передает тепло кипятильнику с водой при t₂ = 100 °С. Сколько воды надо заморозить, чтобы испарить m = 1 кг воды? [ ≅ 5 кг ] 33.11. Над идеальным одноатомным газом проводят процесс 1 – 2 – 3 – 1 (рис.). Найти КПД цикла. [ 1/13 ]

33.12. С идеальным газом проводят процесс 1 – 2 – 3 – 4 – 1 (рис.). Участки 1 – 2 и 3 – 4 – изотермы, а участок 1 – 3 – адиабата. КПД цикла 1 – 2 – 3 – 1 равен η₁, а КПД цикла 1 – 3 – 4 – 1 равен η₂. Чему равен КПД цикла 1 – 2 – 3 – 4 – 1? [смотрите ответ в общем файле темы]

33.13. После переделки тепловой машины периодического действия ее мощность увеличилась на α = 10 %. Причем энергия, получаемая от нагревателя не изменилась, а отдаваемая холодильнику уменьшилась на β = 15 %. На сколько изменился к.п.д. машины? [6%]

Источник

Второе начало термодинамики. Энтропия.

· К. п. д. тепловой машины:

,

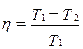
где T₁, T₂ — температуры нагревателя и холодильника.

· Приращение энтропии системы:

· Основное уравнение термодинамики для обратимых процессов:

· Связь между энтропией и статистическим весом Ω (термодинами­ческой вероятностью):

3.2. В каком случае к.п.д. цикла Карно повысится больше: при увеличении температуры нагревателя на ΔТ или при уменьшении температу­ры холодильника на такую же величину?

Ответ: при уменьшении температуры холодильника Т₂.

3.3. Водород совершает цикл Карно. Найти к.п.д. цикла, если при адиабатическом расширении:

а) объем газа увеличивается в п = 2,0 раза;

б) давление уменьшается в n = 2,0 раза.

Ответ: a) η = 1 – n 1-γ = 0,25; б) η = 1 – n 1/(γ-1) = 0,18

3.4. Холодильная машина, работающая по обратному циклу Карно, должна поддерживать в своей камере температуру —10° Спри темпера­туре окружающей среды 20° С. Какую работу надо совершить над ра­бочим веществом машины, чтобы отвести от ее камеры Q₂ = 140 кДж тепла?

3.5. Тепловую машину. работающую по циклу Карно с к.п.д. η 10% используют при тех же тепловых резервуарах как холодильную машину. Найти ее холодильный коэффициент ε.

3.6.Найти к.п.д. цикла, состоящего из двух изобар и двух адиабат, если в пределах цикла давление изменяется в п раз. Рабочее вещество идеальный газ с показателем адиабаты γ.

3.7.Идеальный газ с показателем адиабаты γ, совершает цикл, со­стоящий из двух изохор и двух изобар. Найти к.п.д. такого цикла, если температура Т газа возрастает в п раз как при изохорическом нагреве, так и при изобарическом расширении.

3.8.Идеальный газ совершает цикл, состоящий из:

а) изохоры, адиабаты и изотермы;

б) изобары, адиабаты и изотермы,

причем изотермический процесс происходит при минимальной тем­пературе цикла. Найти к.п.д. каждого цикла, если температура в его пределах изменяется в п раз.

3.9.Идеальный газ с показателем адиабаты γ совершает прямой цикл, состоящий из адиабаты. изобары и изохоры. Найти к.п.д. цикла, если при адиабатическом процессе объем идеального газа:

а) увеличивается в n раз:

б) уменьшается в n раз.

3.10.Воспользовавшись неравенством Клаузиуса, показать, что к.п.д. всех циклов, у которых одинакова максимальная температура Т_maxи одинакова минимальная температура Т_min, меньше, чем у цикла Карно при Т_max и Т_min. Указание: Учесть, что неравенство ∫δQ₁/T₁ — ∫δQ ′ ₂/T₂ ≤ 0 только усиливается при замене Т₁на Т_max и Т₂на Т_min.

3.11.Какую максимальную работу может произвести тепловая ма­шина, если в качестве нагревателя используется кусок железа массы m = 100 кг с начальной температурой Т₁ =1500 К. а в качестве хо­лодильника вода океана с температурой Т₂ = 285 К?

3.12.В качестве основных переменных, характеризующих состояние тела, можно принять его температуру и энтропию. Изобразить графиче­ски цикл Карно на диаграмме, откладывая по оси абсцисс энтропию, а по оси ординат температуру. Вычислить с помощью этого графика к.п.д. цикла.

3.13.Найти изменения энтропии моля идеального газа при изохорическом, изотермическом и изобарическом процессах.

3.14.Найти изменение энтропии при переходе 80 г кислорода от объема 10 л при температуре 80 о C к объему в 40 л при температуре 300 о C.

Ответ:

Ответ:

3.16. Доказать, что энтропия v молей идеального газа может быть представлена в виде: S = v[c_V lnT + Rln(V/v) + const], где аддитивная постоянная в скобках не зависит от числа частиц газа.

3.17.В двух сосудах одного и того же объема находятся различные идеальные газы. Масса газа в первом сосуде m₁во втором – m₂, давление газов и температуры их одинаковы. Сосуды соединили друг с другом, и начался процесс диффузии. Определить суммарное изменение ΔS энтро­пии рассматриваемой системы, если относительная молекулярная масса первого газа μ_1, а второго μ₂.

3.18.Теплоизолированный цилиндрический сосуд разделен поршнем пренебрежимо малой массы на две равные части. По одну сторону порш­ня находится идеальный газ с массой m, относительной молекулярной массой μ и молярными теплоемкостями C_p и С_v,не зависящими от темпе­ратуры, а по другую сторону поршня создан высокий вакуум. Начальные температура и давление газа T₀ и p₀. Поршень отпускают, и он, свободно двигаясь, дает возможность газу заполнить весь объем цилиндра. После этого, постепенно увеличивая давление на поршень, медленно доводят объем газа до первоначальной величины. Найти изменение внутренней энергии н энтропии газа при таком процессе.

3.21.Доказать соотношения Максвелла:

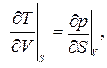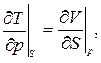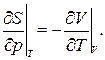3.22.В чем ошибочность следующего рассуждения? Элементарное количество тепла dQ,полученное физически однород­ным телом при квазистатическом процессе, равно

или

Отсюда

Приравнивая оба выражения, получим (∂V/∂T)_p= 0. Отсюда следует, что тепловое расширение тел невозможно.

3.23.Показать, что внутренняя энергия вещества с уравнением состо­яния в форме р = f(V)T не зависит от объема.

3.24.Внутренняя энергия и единицы объема является функцией толь­ко от T, а уравнение состояния газа имеет вид р = и(Т)/3Определить функциональную форму и(Т).

3.25.Для идеального электронного газа имеет место соотношение: PV = 2 /₃U. Найти для этого газа уравнение адиабаты: а) в перемен­ных (Р, V); б) в переменных (V, Т).

3.26.Показать, что для веществ, у которых давление является линей­ной функцией температуры Т, теплоемкость Сv не зависит от объема.

3.27.Используя соотношения Максвелла найти выражение для энтро­пии моля газа Ван-дер-Ваальса.

Ответ:

3.28.Вычислить плотность энтропии S поля теплового излучения.

3.29.Найти отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах.

Ответ:

Ответ: 300 о К.

а) вероятность того, что все атомы соберутся в одной половине сосуда;

б) примерное числовое значение N, при котором это событие можно ожидать на протяжении t = 10 10 лет (возраст Вселенной).

3.32.Найти статистический вес наиболее вероятного распределения N = 10 одинаковых молекул по двум одинаковым половинам сосуда. Определить вероятность такого распределения.

3.33.Какое количество тепла необходимо сообщить макроскопической системе, находящейся при температуре Т = 290 K, чтобы при неизменном объеме ее статистический вес увеличился на Δη = 0,1%?

3.34.Один моль идеального газа, состоящего из одноатомных моле­кул, находится в сосуде при температуре T₀= 300 K. Как и во сколько раз изменится статистический вес этой системы (газа), если ее нагреть изохорически на ΔT = 1,0 K?

Источник

Холодильная машина работающая по обратному циклу карно должна поддерживать в своей камере

Предположим для простоты, что необратимость цикла обусловлена тем, что теплообмен между рабочим телом и источником теплоты (считаем холодильник тоже «источником», только отрицательной температуры) происходит при конечных разностях температур, т.е. нагреватель, отдавая тепло, охлаждается на ∆T, а холодильник нагревается на ΔТ.

Любой процесс, не удовлетворяющий условию обратимости, мы называем необратимым процессом. Примером необратимого процесса является процесс торможения тела под действием сил трения. При этом скорость тела уменьшается, и оно останавливается. Энергия механического движения тела расходуется на увеличение энергии хаотического движения частиц тела и окружающей среды. Происходит диссипация энергии. Для продолжения движения необходим компенсирующий процесс охлаждения тела и среды. В нашем случае тепловых машин, нагреватель и холодильник – не идеальны, они не обладают бесконечной теплоёмкостью и в процессе работы получают или отдают добавочную температуру ΔТ.

На рисунке 5.6 изображен один из таких необратимых циклов.

Для обратимого цикла Карно

Холодильная машина

Холодильная машина – это машина, работающая по обратному циклу Карно (рис. 5.4). То есть если проводить цикл в обратном направлении, тепло будет забираться у холодильника и передаваться нагревателю (за счет работы внешних сил).

Обратный цикл Карно можно рассмотреть на примере рис. 5.5. При изотермическом сжатии В–А, от газа отводится количество теплоты Q₁ при Т₁. В процессе изотермического расширения D–С к газу подводится количество теплоты Q₂.

В этом цикле , и работа, совершаемая над газом, отрицательна, т.е.

Для холодильных машин, работающих по циклу Карно

Доступны следующие дополнительные демонстрации: 1. Гидравлическая машина. 2. Гидростатическое давление.

Источник

Физические основы молекулярно-кинетической теории и термодинамики

5.202. Идеальная холодильная машина работает как тепловой насос по обратному циклу Карно. При этом она берет тепло от воды с температурой t₂ = 2° С и передает его воздуху с температурой t₁ = 27° С. Найти: а) коэффициент n₁ — отношение

количества теплоты, переданного воздуху за некоторый промежуток времени, к количеству теплоты, отнятому за это же время от воды; б) коэффициент n₂ — отношение количества теплоты,

отнятого за некоторый промежуток времени от воды, к затраченной на работу машины энергии за этот же промежуток времени (коэффициент n₂ называется холодильным коэффициентом машины); в) коэффициент — n₃ отношение

затраченной на работу машины энергии за некоторый промежуток времени к количеству теплоты, переданному за это же время воздуху (коэффициент n₃ — к. п. д. цикла). Найти соотношение между коэффициентами n₁, n₂ и n₃.

5.203. Идеальная холодильная машина, работающая по обратному циклу Карно, передает тепло от холодильника с водой при температуре t₂ = 0° С кипятильнику с водой при

температуре t₁=100° С. Какую массу m₂ воды нужно заморозить в холодильнике, чтобы превратить в пар массу m₁ = 1 кг воды в кипятильнике?

5.204. Помещение отапливается холодильной машиной, работающей по обратному циклу Карно. Во сколько раз количество теплоты Q, получаемое помещением от сгорания

дров в печке, меньше количества теплоты Q’, переданного

5.205. Рабочий цикл идеальной паровой машины изображен на рисунке. В начале доступа пара из котла в цилиндр давление в нем возрастает при V₀ = const от p₀ до p₁ (ветвь АВ). При

дальнейшем поступлении пара до объема V_x поршень движется

слева направо при p₁ = const (ветвь ВС). При дальнейшем

поршень выталкивает оставшийся пар при p₀ = const; объем при этом уменьшается от V₂ до V₀ (ветвь ЕА). Найти работу А этой машины, совершаемую за каждый цикл, если V₀=0,5л.

5.206. Паровая машина мощностью Р=14,7 кВт потребляет за время t = 1 ч работы массу m = 8,1 кг угля с удельной теплотой сгорания q = 33 МДж/кг. Температура котла t₁ = 200° С, температура холодильника t₂ = 58° С. Найти фактический к. п. д. n машины и сравнить его с к. п. д. //’ идеальной тепловой

машины, работающей по циклу Карно между теми же температурами.

5.207. Паровая машина мощностью Р = 14,7 кВт имеет площадь поршня S = 0,02 м 2 ; ход поршня h = 45 см. Изобарический процесс ВС (рис.) происходит при движении поршня на одну треть его хода. Объемом V₀, по сравнению с объемами

V₁ и V₂, пренебречь. Давление пара в котле = 1,6 МПа, давление пара в холодильнике p₂ = 0.1 МПа. Сколько циклов за время t = 1 мин делает машина, если показатель адиабаты ? = 1,3?

5.208. Цикл карбюраторного и газового четырехтактного двигателя внутреннего сгорания изображен на рисунке. При

5.210. В цилиндрах карбюраторного двигателя внутреннего сгорания газ сжимается политропически так, что после сжатия температура газа становится равной t₂ = 427° С. Начальная

температура t_x = 140° С газа. Степень сжатия V₂/V₁ = 58. Найти показатель политропы n.

5.211. Диаметр цилиндра карбюраторного двигателя внутреннего сгорания D = 10 см, ход поршня h = 11 см. Какой объем V должна иметь камера сжатия, если известно, что начальное давление газа /?, = 0,1 МПа, начальная температура газа

/, = 127° С и давление в камере после сжатия p₂ = 1 МПа? Какова

будет температура t₂ газа в камере после сжатия? Найти работу

5.212. Найти к. п. д. n карбюраторного двигателя внутреннего сгорания, если показатель политропы n = 1,33 и степень сжатия: а) V₁ / V₂ = 4;б) V₁ / V₂ = 6; в) V₁ / V₂ = 8.

5.213. Карбюраторный двигатель мощностью Р = 735.5 Вт потребляет за время t = 1ч минимальную массу m = 265 г бензина. Найти потери бензина на трение, теплопроводность и пр. Степень сжатия V₁/V₂ = 6,2. Удельная теплота сгорания бензина q = 46 МДж. Показатель политропы n = 1,2.

5.214. Цикл четырехтактного двигателя Дизеля изображен на рисунке. Ветвь АВ — в цилиндры засасывается воздух (^₀=0,1МПа). Ветвь ВС — воздух адиабатически сжимается до давления p_х. В конце такта сжатия в цилиндры впрыскивается топливо, которое воспламеняется в горячем воздухе и сгорает, при этом поршень движется вправо, сначала изобарически (ветвь CD ), а затем адиабатически (ветвь DE). В конце адиабатического расширения открывается выпускной клапан, давление падает до p₀ (ветвь ЕВ ). При движении поршня влево смесь удаляется из цилиндров (ветвь ВА). Найти к.п.д. n двигателя Дизеля.

5.215. Двигатель внутреннего сгорания Дизеля имеет степень адиабатического сжатия е = 16 и степень адиабатического расширения 8 = 6,4. Какую минимальную массу m нефти потребляет двигатель мощностью Р = 36,8 кВт за время / = 1ч? Показатель адиабаты у = 1,3. Удельная теплота сгорания нефти q = 46 МДж/кг.

5.217. Найти изменение dS энтропии при превращении массы m = 1 г воды (t = 0° С) в пар (t_n = 100° С).

5.218. Найти изменение dS энтропии при плавлении массы m = 1кг льда ( t = 0° С).

5.219. Массу m = 640г расплавленного свинца при температуре плавления t_пл вылили на лед (t = 0°С). Найти изменение dS энтропии при этом процессе.

5.220. Найти изменение dS энтропии при переходе массы m = 8 г кислорода от объема V₁ = 10 л при температуре t₁ = 80° С к объему V₂ = 40 л при температуре t₂ = 300° С.

Ошибка в тексте? Выдели её мышкой и нажми

Источник