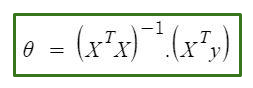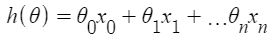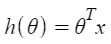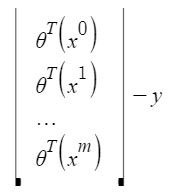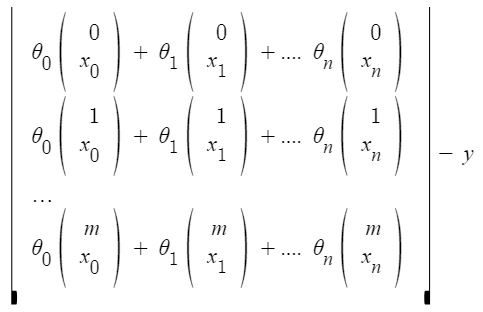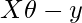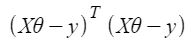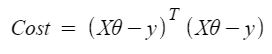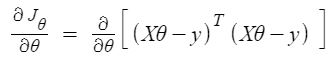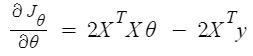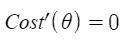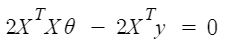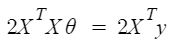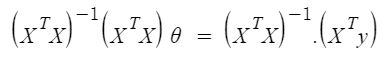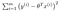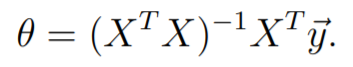normal equation машинное обучение
Normal Equation
Given a matrix equation, the normal equation is one which minimizes the sum of the square differences between the left and right sides
Basics of Machine Learning Series
Introduction
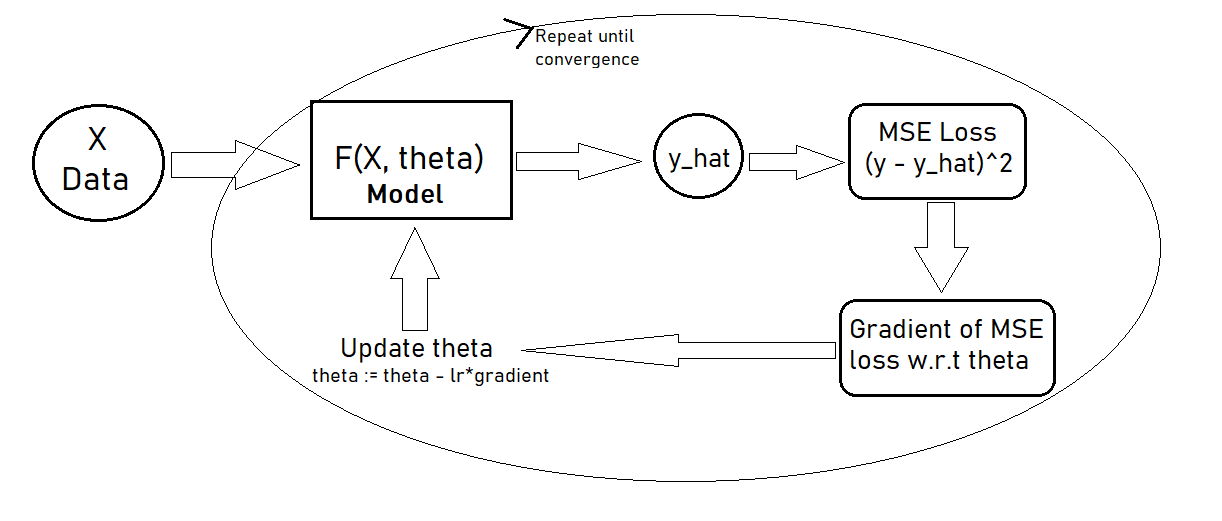
Gradient descent is an algorithm which is used to reach an optimal solution iteratively using the gradient of the loss function or the cost function. In contrast, normal equation is a method that helps solve for the parameters analytically i.e. instead of reaching the solution iteratively, solution for the parameter \(\theta\) is reached at directly by solving the normal equation.
Intuition
Consider a one-dimensional equation for the cost function given by,
According to calculus, one can find the minimum of this function by calculating the derivative and solving the equation by setting derivative equal to zero, i.e.
Similarly, extending (1) to multi-dimensional setup, the cost function is given by,
And similar to (2), the minimum of (3) can be found by taking partial derivatives w.r.t. individual \(\theta_i \forall i \in (0, 1, 2, \cdots, n) \) and solving the equations by setting them to zero, i.e.
Through derivation one can find that \(\theta\) is given by,
Feature scaling is not necessary for the normal equation method. Reason being, the feature scaling was implemented to prevent any skewness in the contour plot of the cost function which affects the gradient descent but the analytical solution using normal equation does not suffer from the same drawback.
Comparison between Gradient Descent and Normal Equation
Given m training examples, and n features
| Gradient Descent | Normal Equation |
|---|---|
| Proper choice of \(\alpha\) is important | \(\alpha\) is not needed |
| Iterative Method | Direct Solution |
| Works well with large n. Complexity of algorithm is O(\(kn^2\)) | Slow for large n. Need to compute \((X^TX)^<-1>\). Generally the cost for computing the inverse is O(\(n^3\)) |
Generally if the number of features is less than 10000, one can use normal equation to get the solution beyond which the order of growth of the algorithm will make the computation very slow.
Non-invertibility
Matrices that do not have an inverse are called singular or degenerate.
Reasons for non-invertibility:
Calculating psuedo-inverse instead of inverse can also solve the issue of non-invertibility.
Implementation
Derivation of Normal Equation
Given the hypothesis,
Let X be the design matrix wherein each row corresponds to the features in \(i^
Since \(X\theta\) and \(y\) both are vectors, \((X\theta)^Ty = y^T(X\theta)\). So (7) can be further simplified as,
Normal Equation in Linear Regression
Author(s): Saniya Parveez
Machine Learning
Gradient descent is a very popular and first-order iterative optimization algorithm for finding a local minimum over a differential function. Similarly, the Normal Equation is another way of doing minimization. It does minimization without restoring to an iterative algorithm. Normal Equation method minimizes J by explicitly taking its derivatives concerning theta j and setting them to zero.
Below is a data-set to predict house price:
Gradient Descent Vs Normal Equation
Gradient Descent
Normal Equation
Linear Regression with Normal Equation
Load the Portland data
Visualize The Area against the Price:
Visualize the Number of Rooms against the Price of the House:
Here, the relationship between the Number of Rooms, and the Price of the House, appears to be Linear.
Define Feature Matrix, and Outcome/Target Vector:
Visualize Cost Function:

Split Data
Normal Equation
Prediction using Normal Equation theta value
Prediction using Linear Regression
Here, the predictions from the Normal Equation and Linear Equation are the same.
Normal Equation Non-Invertibility
A squared matrix that does not have an inverse a matrix is singular if and only if it is determined is zero.
The inverse of Matrix:

Problem due to Non-Invertibility:
How to solve if there are too many features?
Conclusion
Gradient Descent gives one way to minimizing J. Normal Equation is another way of doing minimization. It does minimization without restoring to an iterative algorithm. But, Normal Equation is very slow if the data-set size is very large
Normal Equation in Linear Regression was originally published in Towards AI — Multidisciplinary Science Journal on Medium, where people are continuing the conversation by highlighting and responding to this story.
ML | Normal Equation in Linear Regression
Normal Equation is an analytical approach to Linear Regression with a Least Square Cost Function. We can directly find out the value of θ without using Gradient Descent. Following this approach is an effective and time-saving option when are working with a dataset with small features.
Normal Equation is a follows :
Attention reader! Don’t stop learning now. Get hold of all the important Machine Learning Concepts with the Machine Learning Foundation Course at a student-friendly price and become industry ready.
In the above equation,
θ: hypothesis parameters that define it the best.
X: Input feature value of each instance.
Y: Output value of each instance.
Maths Behind the equation –
Given the hypothesis function
where,
n: the no. of features in the data set.
x0: 1 (for vector multiplication)
Notice that this is a dot product between θ and x values. So for the convenience to solve we can write it as :
The motive in Linear Regression is to minimize the cost function :
where,
x i : the input value of i ih training example.
m: no. of training instances
n: no. of data-set features
y i : the expected result of i th instance
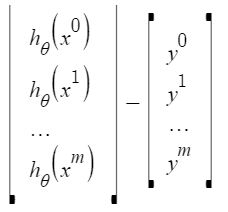
Let us representing the cost function in a vector form.
we have ignored 1/2m here as it will not make any difference in the working. It was used for mathematical convenience while calculation gradient descent. But it is no more needed here.
x i j: value of j ih feature in i ih training example.
This can further be reduced to
But each residual value is squared. We cannot simply square the above expression. As the square of a vector/matrix is not equal to the square of each of its values. So to get the squared value, multiply the vector/matrix with its transpose. So, the final equation derived is
Therefore, the cost function is
So, now getting the value of θ using derivative
So, this is the finally derived Normal Equation with θ giving the minimum cost value.
Русские Блоги
[Машинное обучение Примечания 1.1] Решение нормальных уравнений линейной регрессии
Обзор линейной регрессии
Давайте сначала рассмотрим простейший случай, т. Е. Количество входных атрибутов только одно, и линейная регрессия пытается научиться [1].
Теперь запрос E ( w → ) » role=»presentation» style=»position: relative;»> E ( w → ) Минимальное значение E ( w → ) » role=»presentation» style=»position: relative;»> E ( w → ) Верный w → » role=»presentation» style=»position: relative;»> w → производный
Пример кода
Как судить о качестве модели
Почти любой набор данных может быть смоделирован с помощью вышеуказанного метода, так как оценить качество этих моделей? [2] Сравните два подграфа на рисунке ниже.Если вы выполните линейную регрессию для двух наборов данных, вы получите точно такую же модель (подгонка по прямой линии). Очевидно, что эти данные разные, так насколько эффективны модели на этих двух? Как мы должны сравнивать эти эффекты? Существует способ вычислить степень соответствия между предсказанным значением последовательности yHat и истинным значением последовательности y, то есть вычислить коэффициент корреляции двух последовательностей.
Решите матрицу времени с помощью нормальных уравнений X T X » role=»presentation» style=»position: relative;»> X T X Необратимое решение
Что касается необратимой матрицы, мы также называем ее особой или вырожденной матрицей. Необратимая матрица обычно имеет следующее [3-4.7]:
Кроме того, метод градиентного спуска также может быть использован для решения оптимального решения, когда матрица необратима (me: реальное решение, полученное с помощью нормального уравнения, оптимальное решение, полученное с помощью градиентного спуска). Сравнение градиентного спуска и нормального уравнения показано в следующей таблице: [3-4.6]
Normal Equation in Python: The Closed-Form Solution for Linear Regression
Machine Learning from scratch: Part 3
Mar 23 · 5 min read
In this article, we will implement the Normal Equation which is the closed-form solution for the Linear Regression algorithm where we can find the optimal value of theta in just one step without using the Gradient Descent algorithm.
We will first recap with Gradient Descent Algorithm, then talk about calculating theta using a formula called Normal Equation and finally, see the Normal Equation in Action and plot predictions for our randomly generated data.
Machine Learning from scratch series —
Linear Regression from scratch in Python
Machine Learning from Scratch: Part 1
Locally Weighted Linear Regression in Python
Machine Learning from Scratch: Part 2
Gradient Descent Recap
Gradient Descent Algorithm—
First, we initialize the parameter theta randomly or with all zeros. Then,
Normal Equation
Gradien t Descent is an iterative algorithm meaning that you need to take multiple steps to get to the Global optimum (to find the optimal parameters) but it turns out that for the special case of Linear Regression, there is a way to solve for the optimal values of the parameter theta to just jump in one step to the Global optimum without needing to use an iterative algorithm and this algorithm is called the Normal Equation. It works only for Linear Regression and not any other algorithm.
Normal Equation is the Closed-form solution for the Linear Regression algorithm which means that we can obtain the optimal parameters by just using a formula that includes a few matrix multiplications and inversions.
This is the Normal Equation —
If you know about the matrix derivatives along with a few properties of matrices, you should be able to derive the Normal Equation for yourself.
You might think what if X is a non-invertible matrix, which usually happens if you have redundant features i.e your features are linearly dependent, probably because you have the same features repeated twice. One thing you can do is go and find out which features are repeated and fix them or you can use the np.pinv function in NumPy which will also give you the right answer.
The Algorithm
Check the shapes of X and y so that the equation matches up.
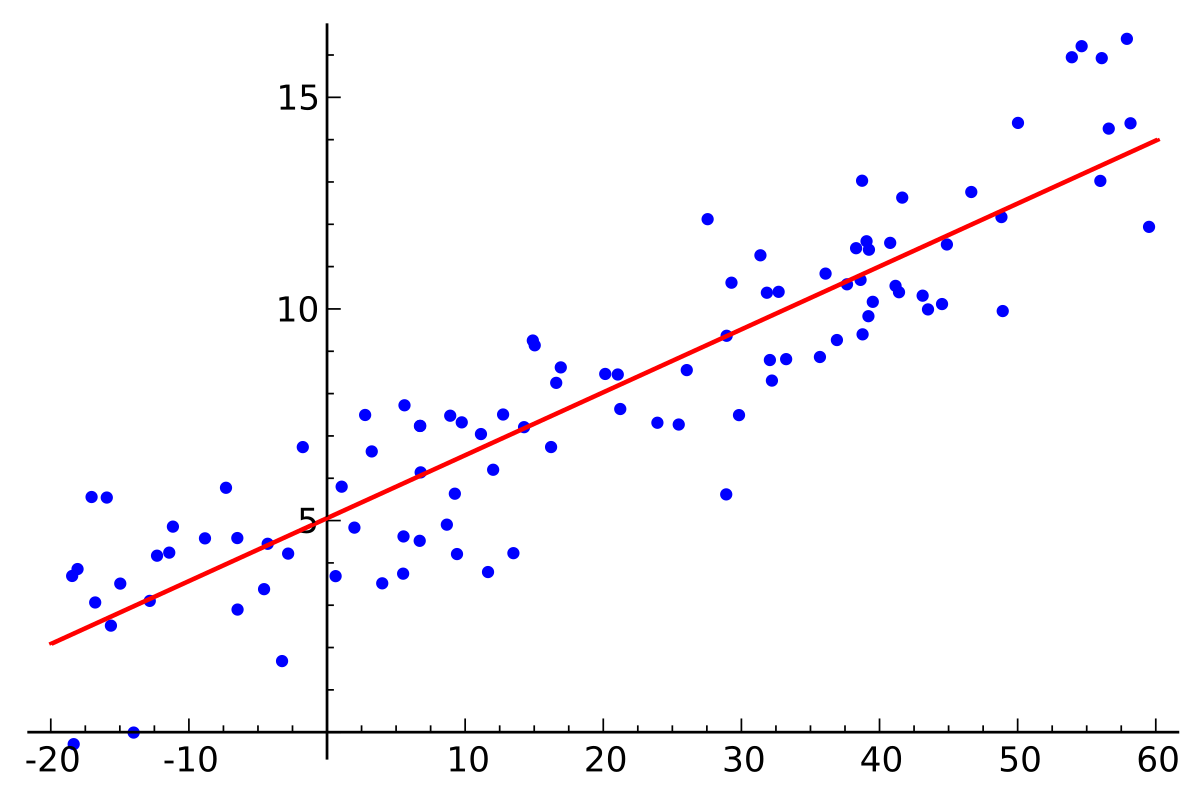
Normal Equation in Action
Let’s take the following randomly generated data as a motivating example to understand the Normal Equation.
Here, n =1 which means the matrix X has only 1 column and m =500 means X has 500 rows. X is a (500×1) matrix and y is a vector of length 500.
Find Theta Function
Let’s write the code to calculate theta using the Normal Equation.