python машинное обучение с подкреплением
Обучение с подкреплением на Python: Пример не из «качалки»
Постановка задачи
Обучение с подкреплением молодая и бурно растущая дисциплина. Это обстоятельство привело к тому, что информации об этом мало на английском и почти нет на русском языке. Особенно, если дело касается объектно-ориентированного подхода, и практических задач не из арсенала Open Gym. Стало интересно, как решать задачи RL в других средах.
Представляю вам результат простой задачи, которая как я надеюсь, убережет вас от части шишек встречающихся на этом интересном пути.
Предположим задачу, в которой нано робот с антибиотиком должен подобраться к скоплению патогенных бактерий для их уничтожения.
Загрузим Reinforsment Learning от Keras и библиотеку для анимации.
Среда
Для обучения с подкреплением требуется среда и агент.
Средой в нашем случае будет мигрирующие в тканях патогены. Их движение соответствует роевому поведению.
Роевое поведение описано моделью Вичека (1995 г.).С помощью этой системы можно имитировать скопления бактерий, поведение стаи птиц или косяка рыб, а также увидеть, как из простых правил появляются само упорядоченные движения.
Возьмем описание модели из статьи Создание собственной симуляции активной материи на Python. И перепишем ее используя объектно-ориентированный подход. Предполагается, что вы уже знакомы с ООП для Python.
Описанный класс послужит нам для описания состояния среды state. Не путайте observation и state. Наблюдаемые данные observation, это только то, что наблюдает агент. Состоянием state считается вся среда: описание всех наших бактерий.
Для правильной работы в автоматическом режиме требуется через атрибуты класса action_space и observation_space описать допустимые значения action агента и представление среды observation.
Их надо наследовать от класса rl.Space. Для action_space требуется переписать методы:
В атрибуте shape классов мы будем хранить форму значений
Для того чтобы сделать среду нам надо создать класс наследуя ее из базового класса среды rl.Env предоставляемой керас. Это абстрактный класс, в соответствии с задуманной средой необходимо описать его методы:
В классе среды мы должны описать состояние state, наблюдение observation, награду reward.
В observation подадим 5 переменных:
Количество «захваченных» бактерий внутри радиуса R
Средний угол направления бактерий внутри R
Угол направления на центр бактерий внутри R
Угол направления на центр бактерий внутри круга R-1.5R
Текущий угол направления нано робота
Действием,- будет угол движения нано робота. Все переменные нормализуем делением на Pi.
На этом этапе, давайте определим параметры среды и проиграем случайные эпизоды.

Просмотр эпизодов даст понимание с каким разнообразием ситуаций успевает столкнуться наш робот. В зависимости от этого, регулируем: количество бактерий; размер площадки; скорость и количество эпох.
Вы можете это сделать в ноутбуке Google Collab.
Агент и обучение
Среда определена. Остается создать агента.
Для решения задачи используем метод Deep Deterministic Policy Gradient (DDPG), его можно рассматривать как DQN для непрерывных пространств действий. Мы попеременно обучаем 2 сети Актера(производит действие action) и Критика(оценивает вознаграждение reward).
Для тренировки используется keras-rl класс DDPGAgent. Он берет на себя всю техническую реализацию, а нам остается написать несколько строчек кода и получить результат. ООП великая сила!
Результат
Давайте посмотрим на действия обученного нано робота. Изменим для наглядности параметры среды

Выводы
При планировании актера, если существует непрерывный допустимый диапазон органов управления, последний нейрон лучше зажать активациями sigmoid(0,1) или tanh(-1,+1) вместо linear. Затем в step() среды развернуть до требуемого диапазона.
Отдельно надо отметить, что набор подаваемых данных должен быть адекватен задаче. Не получится научить агента вождению не показывая дороги. В нашем случае пришлось показать бактерии ситуацию чуть за пределами радиуса R. Без этого наш робот просто тащился за последней бактерией в рое, боясь быть наказанным и не понимая как получить награду.
Через тернии лежит путь к звездам. Буду рад, если кому-то помог разобраться в этой интереснейшей теме.
Введение в обучение с подкреплением: от многорукого бандита до полноценного RL агента
Привет, Хабр! Обучение с подкреплением является одним из самых перспективных направлений машинного обучения. С его помощью искусственный интеллект сегодня способен решать широчайший спектр задач: от робототехники и видеоигр до моделирования поведения покупателей и здравоохранения. В этой вводной статье мы изучим главную идею reinforcement learning и с нуля построим собственного самообучающегося бота.
Введение
Основное отличие обучения с подкреплением (reinforcement learning) от классического машинного обучения заключается в том, что искусственный интеллект обучается в процессе взаимодействия с окружающей средой, а не на исторических данных. Соединив в себе способность нейронных сетей восстанавливать сложные взаимосвязи и самообучаемость агента (системы) в reinforcement learning, машины достигли огромных успехов, победив сначала в нескольких видеоиграх Atari, а потом и чемпиона мира по игре в го.
Если вы привыкли работать с задачами обучения с учителем, то в случае reinforcement learning действует немного иная логика. Вместо того, чтобы создавать алгоритм, который обучается на наборе пар «факторы — правильный ответ», в обучении с подкреплением необходимо научить агента взаимодействовать с окружающей средой, самостоятельно генерируя эти пары. Затем на них же он будет обучаться через систему наблюдений (observations), выигрышей (reward) и действий (actions).
Очевидно, что теперь в каждый момент времени у нас нет постоянного правильного ответа, поэтому задача становится немного хитрее. В этой серии статей мы будем создавать и обучать агентов обучения с подкреплением. Начнем с самого простого варианта агента, чтобы основная идея reinforcement learning была предельно понятна, а затем перейдем к более сложным задачам.
Многорукий бандит
Самый простой пример задачи обучения с подкреплением — задача о многоруком бандите (она достаточно широко освещена на Хабре, в частности, тут и тут). В нашей постановке задачи есть n игровых автоматов, в каждом из которых фиксирована вероятность выигрыша. Тогда цель агента — найти слот-машину с наибольшим ожидаемым выигрышем и всегда выбирать именно ее. Для простоты у нас будет всего четыре игровых автомата, из которых нужно будет выбирать.
По правде говоря, эту задачу можно с натяжкой отнести к reinforcement learning, поскольку задачам из этого класса характерны следующие свойства:
В области обучения с подкреплением есть и другой подход, при котором агенты обучают value functions. Вместо того, чтобы находить оптимальное действие в текущем состоянии, агент учиться предсказывать, насколько выгодно находиться в данном состоянии и совершать данное действие. Оба подхода дают хорошие результаты, однако логика policy gradient более очевидна.
Policy Gradient
Как мы уже выяснили, в нашем случае ожидаемый выигрыш каждого из игровых автоматов не зависит от текущего состояния среды. Получается, что наша нейросеть будет состоять лишь из набора весов, каждый из которых соответствует одному игровому автомату. Эти веса и будут определять, за какую ручку нужно дернуть, чтобы получить максимальный выигрыш. К примеру, если все веса инициализировать равными 1, то агент будет одинаково оптимистичен по поводу выигрыша во всех игровых автоматах.
Для обновления весов модели мы будем использовать e-жадную линию поведения. Это значит, что в большинстве случаев агент будет выбирать действие, максимизирующее ожидаемый выигрыш, однако иногда (с вероятностью равной e) действие будет случайным. Так будет обеспечен выбор всех возможных вариантов, что позволит нейросети «узнать» больше о каждом из них.
Интуитивно понятно, что функция потерь должна принимать такие значения, чтобы веса действий, которые привели к выигрышу увеличивались, а те, которые привели к проигрышу, уменьшались. В результате веса будут обновляться, а агент будет все чаще и чаще выбирать игровой автомат с наибольшей фиксированной вероятностью выигрыша, пока, наконец, он не будет выбирать его всегда.
Реализация алгоритма
Бандиты. Сначала мы создадим наших бандитов (в быту игровой автомат называют бандитом). В нашем примере их будет 4. Функция pullBandit генерирует случайное число из стандартного нормального распределения, а затем сравнивает его со значением бандита и возвращает результат игры. Чем дальше по списку находится бандит, тем больше вероятность, что агент выиграет, выбрав именно его. Таким образом, мы хотим, чтобы наш агент научился всегда выбирать последнего бандита.
Агент. Кусок кода ниже создает нашего простого агента, который состоит из набора значений для бандитов. Каждое значение соответствует выигрышу/проигрышу в зависимости от выбора того или иного бандита. Чтобы обновлять веса агента мы используем policy gradient, то есть выбираем действия, минимизирующие функцию потерь:
Обучение агента. Мы будем обучать агента, путем выбора определенных действий и получения выигрышей/проигрышей. Используя полученные значения, мы будем знать, как именно обновить веса модели, чтобы чаще выбирать бандитов с большим ожидаемым выигрышем:
Полный Jupyter Notebook можно скачать тут.
Решение полноценной задачи обучения с подкреплением
Теперь, когда мы знаем, как создать агента, способного выбирать оптимальное решение из нескольких возможных, перейдем к рассмотрению более сложной задачи, которая и будет представлять собой пример полноценного reinforcement learning: оценивая текущее состояние системы, агент должен выбирать действия, которые максимизируют выигрыш не только сейчас, но и в будущем.
Системы, в которых может быть решена обучения с подкреплением называются Марковскими процессами принятия решений (Markov Decision Processes, MDP). Для таких систем характерны выигрыши и действия, обеспечивающие переход из одного состояния в другое, причем эти выигрыши зависят от текущего состояния системы и решения, которое принимает агент в этом состоянии. Выигрыш может быть получен с задержкой во времени.
Формально Марковский процесс принятия решений может быть определен следующим образом. MDP состоит из набора всех возможных состояний S и действий А, причем в каждый момент времени он находится в состоянии s и совершает действие a из этих наборов. Таким образом, дан кортеж (s, a) и для него определены T(s,a) — вероятность перехода в новое состояние s’ и R(s,a) — выигрыш. В итоге в любой момент времени в MDP агент находится в состоянии s, принимает решение a и в ответ получает новое состояние s’ и выигрыш r.
Для примера, даже процесс открывания двери можно представить в виде Марковского процесса принятия решений. Состоянием будет наш взгляд на дверь, а также расположение нашего тела и двери в мире. Все возможные движения тела, что мы можем сделать, и являются набором A, а выигрыш — это успешное открытие двери. Определенные действия (например, шаг в сторону двери) приближают нас к достижению цели, однако сами по себе не приносят выигрыша, так как его обеспечивает только непосредственно открывание двери. В итоге, агент должен совершать такие действия, которые рано или поздно приведут к решению задачи.
Задача стабилизации перевернутого маятника
Воспользуемся OpenAI Gym — платформой для разработки и тренировки AI ботов с помощью игр и алгоритмических испытаний и возьмем классическую задачу оттуда: задача стабилизации перевернутого маятника или Cart-Pole. В нашем случае суть задачи заключается в том, чтобы как можно дольше удерживать стержень в вертикальном положении, двигая тележку по горизонтали:
В отличии от задачи о многоруком бандите, в данной системе есть:
Таким образом, каждое действие агента будет совершено с учетом не только мгновенного выигрыша, но и всех последующих. Также теперь мы будем использовать скорректированный выигрыш в качестве оценки элемента A (advantage) в функции потерь.
Реализация алгоритма
Импортируем библиотеки и загрузим среду задачи Cart-Pole:
Агент. Сначала создадим функцию, которая будет дисконтировать все последующие выигрыши на текущий момент:
Теперь создадим нашего агента:
Обучение агента. Теперь, наконец, перейдем к обучению агента:
Полный Jupyter Notebook вы можете посмотреть тут. Увидимся в следующих статьях, где мы продолжим изучать обучение с подкреплением!
Обучение с подкреплением для самых маленьких
В данной статье разобран принцип работы метода машинного обучения«Обучение с подкреплением» на примере физической системы. Алгоритм поиска оптимальной стратегии реализован в коде на Python с помощью метода «Q-Learning».
Обучение с подкреплением — это метод машинного обучения, при котором происходит обучение модели, которая не имеет сведений о системе, но имеет возможность производить какие-либо действия в ней. Действия переводят систему в новое состояние и модель получает от системы некоторое вознаграждение. Рассмотрим работу метода на примере, показанном в видео. В описании к видео находится код для Arduino, который реализуем на Python.
Задача
С помощью метода «обучение с подкреплением» необходимо научить тележку отъезжать от стены на максимальное расстояние. Награда представлена в виде значения изменения расстояния от стены до тележки при движении. Измерение расстояния D от стены производится дальномером. Движение в данном примере возможно только при определенном смещении «привода», состоящего из двух стрел S1 и S2. Стрелы представляют собой два сервопривода с направляющими, соединенными в виде «колена». Каждый сервопривод в данном примере может поворачиваться на 6 одинаковых углов. Модель имеет возможность совершить 4 действия, которые представляют собой управление двумя сервоприводами, действие 0 и 1 поворачивают первый сервопривод на определенный угол по часовой и против часовой стрелке, действие 2 и 3 поворачивают второй сервопривод на определенный угол по часовой и против часовой стрелке. На рисунке 1 показан рабочий прототип тележки.

Рис. 1. Прототип тележки для экспериментов с машинным обучением
На рисунке 2 красным цветом выделена стрела S2, синим цветом – стрела S1, черным цветом – 2 сервопривода.

Рис. 2. Двигатель системы
Схема системы показана на рисунке 3. Расстояние до стены обозначено D, желтым показан дальномер, красным и черным выделен привод системы.

Рис. 3. Схема системы
Диапазон возможных положений для S1 и S2 показан на рисунке 4:

Рис. 4.а. Диапазон положений стрелы S1
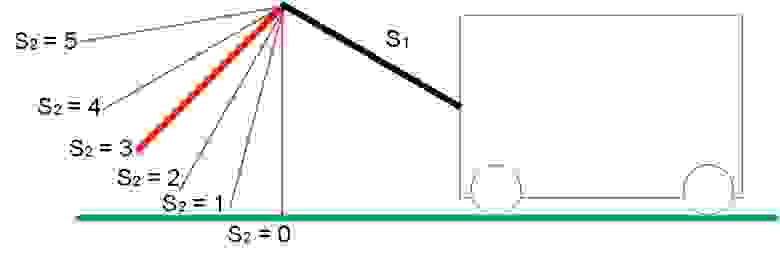
Рис. 4.б. Диапазон положений стрелы S2
Пограничные положения привода показаны на рисунке 5:
При S1 = S2 = 5 максимальная дальность от земли.
При S1 = S2 = 0 минимальная дальность до земли.

Рис. 5. Пограничные положения стрел S1 и S2
У «привода» 4 степени свободы. Действие (action) изменяет положение стрел S1 и S2 в пространстве по определённому принципу. Виды действий показаны на рисунке 6.
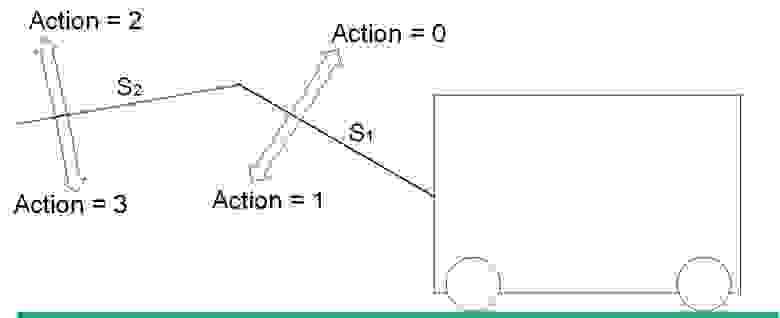
Рис. 6. Виды действий (Action) в системе
Действие 0 увеличивает значение S1. Действие 1 уменьшает значение S1.
Действие 2 увеличивает значение S2. Действие 3 уменьшает значение S2.
Движение
В нашей задаче тележка приводится в движение всего в 2х случаях:
В положении S1 =0, S2 = 1 действие 3 приводит в движение тележку от стены, система получает положительное вознаграждение, равное изменению расстояния до стены. В нашем примере вознаграждение равно 1.

Рис. 7. Движение системы с положительным вознаграждением
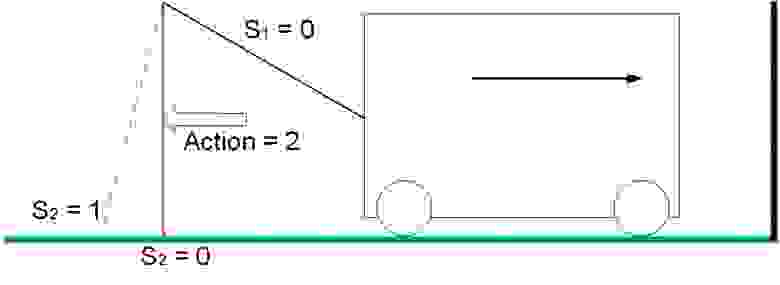
Рис. 8. Движение системы с отрицательным вознаграждением
При остальных состояниях и любых действиях «привода» система будет стоять на месте и вознаграждение будет равно 0.
Хочется отметить, что стабильным динамическим состоянием системы будет последовательность действий 0-2-1-3 из состояния S1=S2=0, в котором тележка будет двигаться в положительном направлении при минимальном количестве затраченных действий. Подняли колено – разогнули колено – опустили колено – согнули колено = тележка сдвинулась вперед, повтор. Таким образом, с помощью метода машинного обучения необходимо найти такое состояние системы, такую определенную последовательность действий, награда за которые будет получена не сразу (действия 0-2-1 – награда за которые равна 0, но которые необходимы для получения 1 за последующее действие 3).
Метод Q-Learning
Основой метода Q-Learning является матрица весов состояния системы. Матрица Q представляет собой совокупность всевозможных состояний системы и весов реакции системы на различные действия.
В данной задаче возможных комбинаций параметров системы 36 = 6^2. В каждом из 36 состояний системы возможно произвести 4 различных действия (Action = 0,1,2,3).
На рисунке 9 показано первоначальное состояние матрицы Q. Нулевая колонка содержит индекс строки, первая строка – значение S1, вторая – значение S2, последние 4 колонки равны весам при действиях равных 0, 1, 2 и 3. Каждая строка представляет собой уникальное состояние системы.
При инициализации таблицы все значения весов приравняем 10.

Рис. 9. Инициализация матрицы Q
После обучения модели (
15000 итераций) матрица Q имеет вид, показанный на рисунке 10.

Рис. 10. Матрица Q после 15000 итераций обучения
Обратите внимание, действия с весами, равными 10, невозможны в системе, поэтому значение весов не изменилось. Например, в крайнем положении при S1=S2=0 нельзя выполнить действие 1 и 3, так как это ограничение физической среды. Эти пограничные действия запрещены в нашей модели, поэтому 10тки алгоритм не использует.
Рассмотрим результат работы алгоритма:
…
Iteration: 14991, was: S1=0 S2=0, action= 0, now: S1=1 S2=0, prize: 0
Iteration: 14992, was: S1=1 S2=0, action= 2, now: S1=1 S2=1, prize: 0
Iteration: 14993, was: S1=1 S2=1, action= 1, now: S1=0 S2=1, prize: 0
Iteration: 14994, was: S1=0 S2=1, action= 3, now: S1=0 S2=0, prize: 1
Iteration: 14995, was: S1=0 S2=0, action= 0, now: S1=1 S2=0, prize: 0
Iteration: 14996, was: S1=1 S2=0, action= 2, now: S1=1 S2=1, prize: 0
Iteration: 14997, was: S1=1 S2=1, action= 1, now: S1=0 S2=1, prize: 0
Iteration: 14998, was: S1=0 S2=1, action= 3, now: S1=0 S2=0, prize: 1
Iteration: 14999, was: S1=0 S2=0, action= 0, now: S1=1 S2=0, prize: 0
Рассмотрим подробнее:
Возьмем итерацию 14991 в качестве текущего состояния.
1. Текущее состояние системы S1=S2=0, этому состоянию соответствует строка с индексом 0. Наибольшим значением является 0.617 (значения равные 10 игнорируем, описано выше), оно соответствует Action = 0. Значит, согласно матрице Q при состоянии системы S1=S2=0 мы производим действие 0. Действие 0 увеличивает значение угла поворота сервопривода S1 (S1 = 1).
2. Следующему состоянию S1=1, S2=0 соответствует строка с индексом 6. Максимальное значение веса соответствует Action = 2. Производим действие 2 – увеличение S2 (S2 = 1).
3. Следующему состоянию S1=1, S2=1 соответствует строка с индексом 7. Максимальное значение веса соответствует Action = 1. Производим действие 1 – уменьшение S1 (S1 = 0).
4. Следующему состоянию S1=0, S2=1 соответствует строка с индексом 1. Максимальное значение веса соответствует Action = 3. Производим действие 3 – уменьшение S2 (S2 = 0).
5. В итоге вернулись в состояние S1=S2=0 и заработали 1 очко вознаграждения.
На рисунке 11 показан принцип выбор оптимального действия.
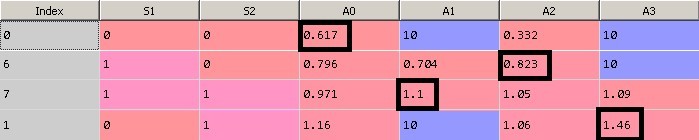
Рис. 11.а. Матрица Q

Рис. 11.б. Матрица Q
Рассмотрим подробнее процесс обучения.
Установим начальное положение колена в крайнее верхнее положение:
Инициализируем матрицу Q, заполнив начальным значением:
Вычислим параметр epsilon. Это вес «случайности» действия алгоритма в нашем расчёте. Чем больше итераций обучения прошло, тем меньше случайных значений действий будут выбраны:
Для первой итерации:
Сохраним текущее состояние:
Получим «лучшее» значение действия:
Рассмотрим функцию поподробнее.
Функция getAction() выдает значение действия, которому соответствует максимальный вес при текущем состоянии системы. Берется текущее состояние системы в матрице Q и выбирается действие, которому соответствует максимальный вес. Обратим внимание, что в этой функции реализован механизм выбора случайного действия. С увеличением числа итераций случайный выбор действия уменьшается. Это сделано, для того, чтобы алгоритм не зацикливался на первых найденных вариантах и мог пойти по другому пути, который может оказаться лучше.
В исходном начальном положении стрел возможны только два действия 1 и 3. Алгоритм выбрал действие 1.
Далее определим номер строки в матрице Q для следующего состояние системы, в которое система перейдет после выполнения действия, которое мы получили в предыдущем шаге.
В реальной физической среде после выполнения действия мы получили бы вознаграждение, если последовало движение, но так как движение тележки моделируется, необходимо ввести вспомогательные функции эмуляции реакции физической среды на действия. (setPhysicalState и getDeltaDistanceRolled() )
Выполним функции:
— моделируем реакцию среды на выбранное нами действие. Изменяем положение сервоприводов, смещаем тележку.
— Вычисляем вознаграждение – расстояние, пройденное тележкой.
После выполнения действия нам необходимо обновить коэффициент этого действия в матрице Q для соответствующего состояния системы. Логично, что, если действие привело к положительной награде, то коэффициент, в нашем алгоритме, должен уменьшиться на меньшее значение, чем при отрицательном вознаграждении.
Теперь самое интересное – для расчета веса текущего шага заглянем в будущее.
При определении оптимального действия, которое нужно совершить в текущем состоянии, мы выбираем наибольший вес в матрице Q. Так как мы знаем новое состояние системы, в которое мы перешли, то можем найти максимальное значение веса из таблицы Q для этого состояния:
В самом начале оно равно 10. И используем значение веса, еще не выполненного действия, для подсчета текущего веса.
Т.е. мы использовали значение веса следующего шага, для расчета веса шага текущего. Чем больше вес следующего шага, тем меньше мы уменьшим вес текущего (согласно формуле), и тем текущий шаг будет предпочтительнее в следующий раз.
Этот простой трюк дает хорошие результаты сходимости алгоритма.
Масштабирование алгоритма
Данный алгоритм можно расширить на большее количество степеней свободы системы (s_features), и большее количество значений, которые принимает степень свободы (s_states), но в небольших пределах. Достаточно быстро матрица Q займет всю оперативную память. Ниже пример кода построения сводной матрицы состояний и весов модели. При количестве «стрел» s_features = 5 и количестве различных положений стрелы s_states = 10 матрица Q имеет размеры (100000, 9).
Вывод
Этот простой метод показывает «чудеса» машинного обучения, когда модель ничего не зная об окружающей среде обучается и находит оптимальное состояние, при котором награда за действия максимальна, причем награда присуждается не сразу, за какое либо действие, а за последовательность действий.
