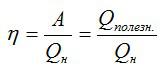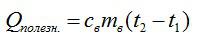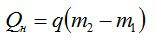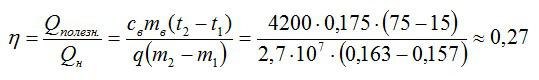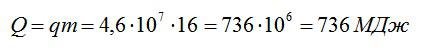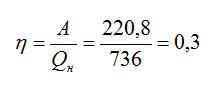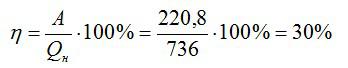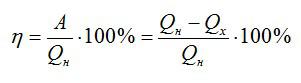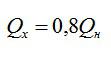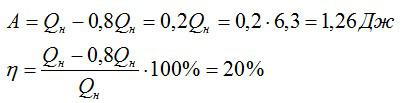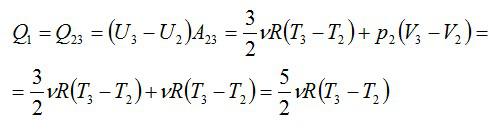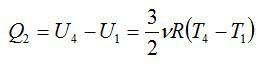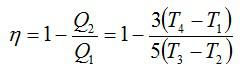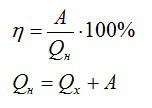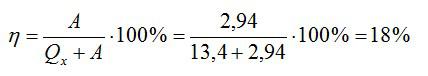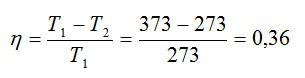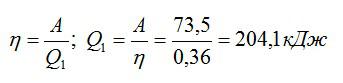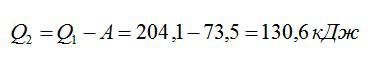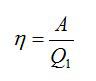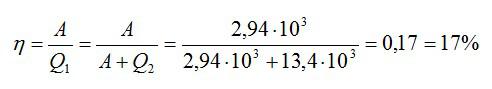Тепловая машина совершила работу в 3 кдж и отдала холодильнику 5 кдж теплоты

Задачи на КПД теплового двигателя: примеры решений

У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.

Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.

Задачи по физике на КПД теплового двигателя

Задача на вычисление КПД теплового двигателя №1

Условие

Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.

Решение

Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:

Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:

Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.

Подставляем значения и вычисляем:

Ответ: 27%

Задача на вычисление КПД теплового двигателя №2

Условие

Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.

Решение

Найдем общее количество теплоты, которое произвел двигатель:

Теперь можно рассчитать КПД:

Или, умножая на 100, получаем значение КПД в процентах:

Ответ: 30%.

Задача на вычисление КПД теплового двигателя №3

Условие

Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.

Решение

КПД идеальной тепловой машины:

Вычислим сначала работу, а затем КПД:

Ответ: 20%; 1,26 Дж.

Задача на вычисление КПД теплового двигателя №4

Условие

Решение

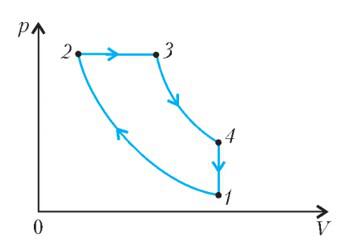
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.

Ответ: См. выше.

Задача на вычисление КПД теплового двигателя №5

Условие

Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.

Решение

Запишем формулу для КПД:

Ответ: 18%

Вопросы на тему тепловые двигатели

Вопрос 1. Что такое тепловой двигатель?

Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.

Вопрос 2. Приведите примеры тепловых двигателей.

Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:

Вопрос 3. Может ли КПД двигателя быть равен единице?

Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.

КПД реальных двигателей редко превышает 30%.

Вопрос 4. Что такое КПД?

Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.

Вопрос 5. Что такое удельная теплота сгорания топлива?

Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.

Задачи и вопросы на цикл Карно

Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.

Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).

Задача на цикл Карно №1

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.

Решение

Рассчитаем КПД цикла:

С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:

Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:

Ответ: 0,36; 204,1 кДж; 130,6 кДж.

Задача на цикл Карно №2

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.

Решение

Формула для КПД цикла Карно:

Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:

Ответ: 17%.

Задача на цикл Карно №3

Условие

Изобразите цикл Карно на диаграмме и опишите его

Решение

Цикл Карно на диаграмме PV выглядит следующим образом:

Ответ: см. выше.

Вопрос на цикл Карно №1

Сформулируйте первую теорему Карно

Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.

Вопрос на цикл Карно №2

Может ли коэффициент полезного действия в цикле Карно быть равным 100%?

Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.

Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Решение задач на КПД теплового двигателя

Содержание

В данном уроке мы разберем решение задач, используя формулы, приведенные выше.

Для решения задач, в условиях которых, говорится о сжигании топлива ($Q = qm$), вам понадобятся табличные значения удельной теплоты сгорания топлива.

Задача №1

Дано:
$m = 300 \space г$
$\Delta t = 200 \degree C$
$c = 460 \frac<Дж><кг \cdot \degree C>$

СИ:
$m = 0.3 \space кг$

Показать решение и ответ

Решение:

Для того чтобы нагреть железную деталь, необходимо сообщить ей некоторое количество теплоты:
$Q = cm(t_2 – t_1) = cm \Delta t$.

Рассчитаем эту энергию:
$Q = 460 \frac<Дж> <кг \cdot \degree C>\cdot 0.3 \space кг \cdot 200 \degree C = 27 \space 600 \space Дж = 27.6 \space кДж$.

Сообщенная энергия будет эквивалентна работе внешних сил:
$A = Q = 27.6 \space кДж$.

Задача №2

Дано:
$t = 1 \space ч$
$N = 733 \space Вт$
$q = 2.7 \cdot 10^7 \frac<Дж><кг>$

СИ:
$t = 3600 \space с$

Показать решение и ответ

Решение:

Мощность по определению:
$N = \frac$.

Выразим отсюда полезную работу, совершаемую машиной, и рассчитаем ее:
$A_п = Nt$,
$A_п = 733 \space Вт \cdot 3600 \space с = 2 \space 638 \space 800 \space Дж \approx 0.26 \cdot 10^7 \space Дж$.

По условиям задачи количество теплоты, которое выделяется при сжигании каменного угля, равно полезной работе:
$A_п = Q = qm$.

Выразим отсюда массу угля и рассчитаем ее:
$m = \frac$,
$m = \frac<0.26 \cdot 10^7 \space Дж><2.7 \cdot 10^7 \frac<Дж><кг>> \approx 0.1 \space кг \approx 100 \space г$.

Задача №3

Дано:
$Q_1 = 120 \space кДж$
$A_п = 30 \space кДж$

СИ:
$Q_1 = 120 \cdot 10^3 \space Дж$
$A_п = 30 \cdot 10^3 \space Дж$

Показать решение и ответ

Решение:

Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac$.

Задача №4

Дано:
$t = 30 \space мин$
$Q_1 = 460 \space МДж$
$Q_2 = 280 \space МДж$

СИ:
$t = 1800 \space с$
$Q_1 = 460 \cdot 10^6 \space Дж$
$Q_2 = 280 \cdot 10^6 \space Дж$

Показать решение и ответ

Решение:

Запишем формулу для расчета КПД теплового двигателя:
$\eta = =\frac = \frac$, где
$A_п$ – полезная работа,
$Q_1$ – количество теплоты, полученное от нагревателя,
$Q_2$ – количество теплоты, отданное холодильнику.

Величина работы также присутствует в определении мощности:
$N = \frac$.

Когда мощность определяется полезной работой, мы называем ее полезной мощностью.

Подставим в формулу мощности определение работы из формулы для КПД и рассчитаем ее:
$N = \frac$,
$N = \frac<460 \cdot 10^6 \space Дж – 280> <1800 \space с>= \frac<180 \cdot 10^6 \space Дж> <1800 \space с>= 0.1 \cdot 10^6 \space Вт = 100 \space кВт$.

Задача №5

Дано:
$N = 367 \space кВт$
$t = 1 \space ч$
$Q_1 = 6720 \space МДж$

СИ:
$N = 367 \cdot 10^3 \space Вт$
$t = 3600 \space с$
$Q_1 = 6720 \cdot 10^6 \space Дж$

Показать решение и ответ

Решение:

Полезная работа, совершенная тепловым двигателем, определяется разностью количества теплоты, отданному холодильнику, и количества теплоты, полученного от нагревателя:
$A_п = Q_1 – Q_2$.

Тогда, количество теплоты, которое получает холодильник будет равно:
$Q_2 = Q_1 – A_п$.

Совершенную работу мы можем определить через мощность:
$N = \frac$,
$A_п = Nt$.

Подставим в формулу для количества теплоты, получаемого холодильником:
$Q_2 = Q_1 – Nt$.

Рассчитаем эту энергию:
$Q_2 = 6720 \cdot 10^6 \space Дж – 367 \cdot 10^3 \space Вт \cdot 3600 \space с = 6720 \cdot 10^6 \space Дж – 1321.2 \cdot 10^6 \space Дж = 5398.8 \cdot 10^6 \space Дж \approx 5400 \space МДж$.

Задача №6

Дано:
$\upsilon = 20 \frac<км><ч>$
$s = 100 \space км$
$m = 1 \space кг$
$\eta = 22 \% = 0.22$
$q = 4.6 \cdot 10^7 \frac<Дж><кг>$

СИ:
$\upsilon \approx 5.6 \frac<м><с>$
$s = 100 \cdot 10^3 \space м$

Показать решение и ответ

Решение:

Мощность по определению:
$N = \frac$.

Полезную работу мы можем выразить из формулы для расчета КПД теплового двигателя:
$\eta = \frac$.

Подставим в формулу для расчета КПД:
$\eta = \frac$.

Выразим отсюда полезную работу:
$A_п = \eta \cdot qm$.

Время, которое необходимо нам для расчета мощности, мы можем найти через перемещение и скорость:
$t = \frac<\upsilon>$.

Задача №7

Дано:
$N = 36.6 \space кВт$
$t = 1 \space ч$
$m = 10 \space кг$
$q = 4.4 \cdot 10^7 \frac<Дж><кг>$

СИ:
$N = 36.6 \cdot 10^3 \space Вт$
$t = 3600 \space с$

Показать решение и ответ

Решение:

Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac \cdot 100 \%$.

Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.

Задача №8

Дано:
$N = 220 \space кВт$
$t = 8 \space ч$
$\eta = 15 \% = 0.15$
$q = 2.7 \cdot 10^7 \frac<Дж><кг>$

СИ:
$N = 220 \cdot 10^3 \space Вт$
$t = 28.8 \cdot 10^3 \space с$

Показать решение и ответ

Решение:

Запишем формулу для расчета КПД:
$\eta = \frac$.

Количество теплоты, полученное от нагревателя – это энергия, выделившаяся при сгорании каменного угля:
$Q_1 = qm$.

Подставим эти выражения в формулу для КПД:
$\eta = \frac$.

Выразим отсюда массу каменного угля:
$m = \frac$.

Задача №9

Дано:
$Q_1 = 12.57 \space МДж$
$t = 1 \space ч$
$N = 735 \space Вт$

СИ:
$Q_1 = 12.57 \cdot 10^6 \space Дж$
$t = 3600 \space с$

Показать решение и ответ

Решение:

Запишем формулу для расчета КПД теплового двигателя:
$\eta = \frac \cdot 100 \%$.

Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.

Подставим выражение для полезной работы в формула для КПД и рассчитаем его:
$\eta = \frac \cdot 100 \%$,
$\eta = \frac<735 \space Вт \cdot 3600 с> <12.57 \cdot 10^6 \space Дж>\cdot 100 \% \approx 21 \%$.

Задача №10

Дано:
$N = 367 \space кВт$
$m = 60 \space т$
$\eta = 30 \% = 0.3$
$q = 4.4 \cdot 10^7 \frac<Дж><кг>$

СИ:
$N = 367 \cdot 10^3 \space Вт$
$m = 60 \cdot 10^3 \space кг$

Показать решение и ответ

Решение:

Формула для расчета КПД теплового двигателя:
$\eta = \frac$.

Количество теплоты, полученное от нагревателя – это энергия, выделившаяся при сгорании нефти:
$Q_1 = qm$.

Подставим эти выражения в формулу для КПД:
$\eta = \frac$.

Выразим отсюда время, за которое была совершена полезная работа:
$t = \frac$.

Источник

Тепловая машина совершила работу в 3 кдж и отдала холодильнику 5 кдж теплоты

Рассмотрим две идеальные тепловые машины. Температуры нагревателя и холодильника первой машины отличаются в 4 раза. Температура холодильника первой тепловой машины равна температуре нагревателя второй тепловой машины. Температура холодильника второй тепловой машины в 5 раз меньше температуры нагревателя первой тепловой машины. Во сколько раз КПД первой машины больше КПД второй машины?

Ответ округлите до сотых долей.

По условию для первой тепловой машины

Для второй тепловой машины

Отсюда получаем:

Рассмотрим две идеальные тепловые машины. Температуры нагревателя и холодильника первой машины отличаются в 4 раза. Температура холодильника первой тепловой машины равна температуре нагревателя второй тепловой машины. Температура холодильника второй тепловой машины в 6 раз меньше температуры нагревателя первой тепловой машины. Во сколько раз КПД первой машины больше КПД второй машины? Ответ округлите до сотых долей.

По условию для первой тепловой машины

Для второй тепловой машины

Отсюда получаем:

Аналоги к заданию № 24098: 24151 Все

Идеальная тепловая машина обменивается теплотой с тёплым телом — окружающей средой, находящейся при температуре +25 °С, и холодным телом с температурой −18 °С. В некоторый момент машину запустили в обратном направлении, так что все составляющие теплового баланса — работа и количества теплоты — поменяли свои знаки. При этом за счёт работы, совершенной двигателем тепловой машины, от холодного тела теплота стала отбираться, а тёплому телу — сообщаться.

Какую работу совершил двигатель тепловой машины, если количество теплоты, отведенной от холодного тела, равно 165 кДж? Ответ округлите до целого числа кДж.

КПД идеальной тепловой машины равен отношению совершенной работы к затраченному количеству теплоты где и — температуры «нагревателя» (теплого тела) и «холодильника» (холодного тела), с которыми обменивается теплотой рабочее вещество цикла. Количество теплоты, которое при этом отдается холодильнику, равно

При работе идеальной тепловой машины в обратном направлении от холодного тела отнимается количество теплоты за счет работы совершаемой над рабочим веществом цикла, и теплому телу, которым в данном случае является окружающая среда, отдается количество теплоты причем все соотношения количеств теплоты, работы и температур остаются такими же, как при работе идеальной тепловой машины в прямом направлении.

Поэтому и

Здравствуйте! Поправьте меня, если я неправильно понял смысл задачи, но на мой взгляд тут явно ошибки в формулировках. В тексте задачи ставится вопрос: «Какую работу совершил двигатель тепловой машины. «. При работе тепловой машины в обратную сторону мы имеем то что описано в решении: «. от холодного тела отнимается количество теплоты Q- за счет работы A, совершаемой над рабочим веществом. «. Всё верно, и так как совершается работа НАД рабочим веществом, то, стало быть, работа САМОГО вещества будет отрицательной. А если мы теперь заглянем в ответ, то увидим там положительный результат. Таким образом, из данного решения следует, что двигатель, отняв теплоту от более холодного тела (тем самым ещё сильнее охладив его), и передав его более горячему (ещё сильнее нагрев его), помимо прочего ещё и совершил ПОЛОЖИТЕЛЬНУЮ работу. Это противоречит обоим постулатам Клаузиуса и Кельвина! Пожалуйста, объясните где я ошибся в рассуждениях, или это неверно составленное решение?

Для холодильника в формуле КПД холодильника работа выполняется внешними силами, а не газом.

Идеальная тепловая машина обменивается теплотой с тёплым телом — окружающей средой, находящейся при температуре +25 °С, и холодным телом с температурой –18 °С. В некоторый момент машину запустили в обратном направлении, так что все составляющие теплового баланса — работа и количества теплоты — поменяли свои знаки. При этом за счёт работы, совершённой двигателем тепловой машины, от холодного тела теплота стала отбираться, а тёплому телу — сообщаться.

Какую работу совершил двигатель тепловой машины, если количество теплоты, сообщенной тёплому телу, равно 193 кДж? Ответ округлите до целого числа кДж.

КПД идеальной тепловой машины равен отношению совершенной работы к затраченному количеству теплоты где и — температуры «нагревателя» (теплого тела) и «холодильника» (холодного тела), с которыми обменивается теплотой рабочее вещество цикла. Количество теплоты, которое при этом отнимается от теплого тела, равно

При работе идеальной тепловой машины в обратном направлении от холодного тела отнимается количество теплоты за счёт работы совершаемой над рабочим веществом цикла, и тёплому телу, которым в данном случае является окружающая среда, отдается количество теплоты причём все соотношения количеств теплоты, работы и температур остаются такими же, как при работе идеальной тепловой машины в прямом направлении.

Поэтому и

Источник