цели обучения математике в средней школе по фгос
Особенности преподавания математики в условиях введения ФГОС ООО
Математическое образование в системе общего среднего образования занимает одно из ведущих мест, что определяется безусловной практической значимостью математики, ее возможностями в развитии и формировании мышления человека, ее вкладом в создание представлений о научных методах познания действительности. Целью обучения математике является наряду с изучением собственно математики развитие универсальных (общих) способностей, умений и навыков, являющихся основой существования человека в социуме.
Просмотр содержимого документа
«Особенности преподавания математики в условиях введения ФГОС ООО»
Особенности преподавания математики в условиях введения
Цели и задачи обучения математике в соответствии с ФГОС.
Математическое образование в системе общего среднего образования занимает одно из ведущих мест, что определяется безусловной практической значимостью математики, ее возможностями в развитии и формировании мышления человека, ее вкладом в создание представлений о научных методах познания действительности. Целью обучения математике является наряду с изучением собственно математики развитие универсальных (общих) способностей, умений и навыков, являющихся основой существования человека в социуме.
В результате изучения предметной области «Математика и информатика» (в нее входит учебный предмет «Математика») обучающиеся развивают логическое и математическое мышление, получают представление о математических моделях; овладевают математическими рассуждениями; учатся применять математические знания при решении различных задач и оценивать полученные результаты; овладевают умениями решения учебных задач; развивают математическую интуицию. Содержание математического образования основной школы формируется на основе Фундаментального ядра школьного математического образования. Оно представлено в виде следующих содержательных разделов: арифметика; алгебра; функции; вероятность и статистика; геометрия. Наряду с этим включены два дополнительных блока: логика и множества; математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся.
2. Особенности организации обучения математике в соответствии с ФГОС.
Очевидно, что новые требования к результатам образовательной деятельности требуют определенных изменений в содержании и организации процесса обучения.
Проектирование УУД в календарно-тематическом планировании представляется принципиально новым элементом деятельности учителя. Каждый учебный предмет раскрывает определенные возможности для формирования УУД. УУД вполне может выступать в качестве предмета обучения; выделяться в тематическом планировании каждого раздела учебной дисциплины и уточняться поурочно в календарно-тематическом планировании. В общем случае УУД должно являться инструментом или способом достижения цели и задач каждого урока. При этом учителю необходимо владеть видами и содержанием каждого из УУД и знать связи между ними.
Действия учителя при планировании учебного занятия:
Выбор УУД в соответствии с целью урока, содержанием учебного материала, технологиями обучения, спецификой учебного предмета, возрастными особенностями учащихся.
Выделение времени для формирования и/или развития УУД в границах учебного занятия или урока.
Определение приемов, методов, способов и форм организации деятельности учащихся для формирования и/или развития УУД.
Проектирование содержания деятельности учащихся для формирования и/или развития УУД через использование системы разнообразных задач и средств их решения.
Еще одной существенной задачей для учителя становится определение ресурсов своего предмета в формировании и совершенствовании УУД: в каких учебных темах, какими средствами формировать те или иные УУД.
Конкретизируем содержание УУД, которые формируются на уроках математики. Следует отметить, что предмет «Математика» направлен, прежде всего, на развитие познавательных универсальных учебных действий. Итак, познавательные УУД:
Общеучебные: построение устных и письменных высказываний, работа с информацией, целеполагание, структурирование знаний, рефлексия, контроль, оценка, создание алгоритмов деятельности, выбор эффективных способов решений.
Логические: формирование понятий, сравнение, сериация, установление причинно-следственных связей, построение логической цепочки, выдвижение гипотез и их доказательство, анализ, синтез, осознание, что такое свойства предмета, умение приводить контрпримеры.
Знаково-символические: замещение, кодирование, декодирование, моделирование, использование знаково-символической записи математического понятия.
Постановка и решение проблемы: формулирование проблемы, создание способов решения проблемы, использование индуктивного умозаключения.
Формирование универсальных учебных действий и является задачей на каждом этапе урока.
Обязательным элементом урока в системно-деятельностном подходе является учебная проблема:
учитель может лично заострить противоречие и сообщить учебную проблему;
учащиеся совершенно самостоятельно осознают противоречие и формулируют проблему;
учитель в диалоге побуждает учеников осознать противоречие и сформулировать учебную проблему.
Т.е. как советует доктор психологических наук Галина Анатольевна Цукерман: «Не давать образцов, ставить ребенка в ситуацию, где его привычные способы действия с очевидностью непригодны, мотивировать поиск существенных особенностей новой ситуации, в которой надо действовать»
3. Структура урока математики по технологии системно-деятельностного подхода
1. Мотивация к учебной деятельности.
Создание настроя и задание мотивации на урок, причины для учёбы, связанной с семантикой ребёнка.
Способы мотивации деятельности детей: вопросы, суждения, ошибки персонажей; задания, для выполнения которых недостаёт знаний; заголовки-вопросы; наблюдения за фактами, в том числе за ошибками, для объяснения которых нужны новые сведения, и др. Учебным действием является лишь то действие, которое «цепляет» ум ученика.
На предыдущем уроке мы делили 28 конфет на 25 человек, и 3 конфеты у нас было в остатке, а сегодня нам нужно одну конфету разделить на двоих, одну шоколадку на троих. Как это сделать?
Пирог, который мама испекла на день рождения Малыша, Карлсон предложил разделить следующим образом: 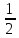
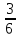
Перед уроком по знакомству с понятием «процент» прошу детей быть очень внимательными один день и посчитать, сколько раз за этот день они услышали или прочитали слово «процент».
2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии
Актуализация изученных способов действий, достаточных для построения нового знания, их обобщение и звуковая фиксация.
Проговаривание, на сколько частей будем делить конфету; на сколько частей шоколадку, какие части получим (половина, треть).
Как выяснить, корректно ли поступает Карлсон? (сравнить 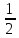
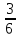
3.Выявление места и причины затруднения.
Учащиеся должны восстановить выполненные операции и зафиксировать (вербально и знаково) место, шаг, операцию, где возникло затруднение; соотнести свои действия с используемым способом действий и на этой основе выявить и зафиксировать во внешней речи причину затруднения.
1 (целую конфету или шоколадку) надо разделить на несколько частей, в жизни можно разломить или разрезать, а как в математике?
Как сравнить 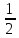
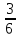
Почему берётся именно сотая часть от целого и как это фиксируется на математическом языке?
4. Построение проекта выхода из затруднения.
Делим целую конфету на две части, каждому достаётся по одной из двух частей; по одной из трёх частей от шоколадки.
Подвод учащихся к тому, что надо в обеих дробях иметь одинаковый знаменатель.
Историческая справка (может быть подготовлена учащимся) о происхождении слова «процент» и знака процента.
Реализация построенного проекта.
Нарисовать целую конфету и целую шоколадку и разделённые на части, подписать. Сделать вывод о делении целого на части, математической записи (понятие дроби, числителя, знаменателя)
Изобразить 100% в виде круга, закрасить разные его части, выраженные в процентах. Сделать вывод о соотношении частей и процентов.
Первичное закрепление с проговариваиием во внешней речи.
Скажи мне, я забываю. Покажи мне, я могу запомнить. Позволь мне сделать это, и это станет моим навсегда (Китайская пословица).
Работа в парах по чтению дробей, проговариванию числителя и знаменателя, по записи частного в виде дроби, выполнению рисунков, нахождению разных способов записи закрашенных частей фигур и не закрашенных.
Работа по сокращению дробей, приведению дробей к общему знаменателю, выполнению рисунков.
Работа по переводу процентов в части, частей в проценты, изображению на рисунках, схемах.
Самостоятельная работа с самопроверкой по эталону.
Сравнивание успехов ученика с его собственным прошлым состоянием, а не с успехами другого.
Включение в систему знаний и повторение.
Дифференцированная работа с учащимися по освоению понятия: «дробь».
Работа по применению правил сокращения дробей и приведению дробей к общему знаменателю.
Работа в группах по решению задач с процентами.
9. Рефлексия учебной деятельности на уроке.
Фиксируется новое содержание, изученное на уроке, организуется рефлексия и самооценка учениками собственной учебной деятельности. Соотносятся ее цель и результаты, намечаются дальнейшие цели деятельности. Проведение так называемой подстройки к будущему (соединить изученный на уроке материал с уже имеющимся в голове у ученика и сориентировать на восприятие будущего нового материала)
На уроке мы узнали основное свойство дроби, научились сокращать дроби и приводить их к общему знаменателю. Мы работали с дробями, у которых числитель меньше знаменателя, а на следующем уроке мы будем работать с дробями, у которых числитель больше знаменателя и узнаем, как они называются.
На уроке мы узнали что такое «процент», а на следующем уроке мы научимся решать задачи на проценты и узнаем, как они помогают нам в жизни.
Исследовательский метод – высший уровень проблемного подхода. Проблемное изложение и проблемная беседа являются подготовкой учащихся к нему. Исследовательский метод в обучении заключается в самостоятельном решении учащимися проблем, трудных задач познавательного и практического характера. При исследовательской деятельности дети отыскивают не только способы решения поставленных проблем, но и побуждаются к самостоятельной их постановке, к выдвижению целей своей деятельности. В качестве примера применения данного метода можно привести исследовательскую работу при изучении темы «Длина окружности и площадь круга» в 6 классе. В результате своей деятельности обучающиеся приходят к выводу: отношение длины окружности к ее диаметру соответствующей окружности есть число постоянное.
Одной из технологий системно-деятельностного подхода, которую мы применяем, является метод проектов, который мы рассматриваем как специальную форму организации познавательной деятельности.
Метод проектов позволяет строить учебный процесс, исходя из интересов обучающихся, дает возможность обучающемуся проявить самостоятельность в планировании, организации и контроле своей учебно-познавательной деятельности. Метод проектов ориентирован на самостоятельную деятельность обучающихся – индивидуальную, парную, групповую, реализующуюся в течение определенного отрезка времени. При выполнении проекта дети решают поставленную проблему, учатся применять знания из различных областей науки, техники. Результаты выполненных проектов являются «осязаемыми»: если это теоретическая проблема, то ее итогом является конкретное решение, если практическая – конкретный результат, готовый к использованию (на уроке, в школе и т.д.). Примерами краткосрочных проектов, реализуемых на одном уроке, могут служить «Ремонт комнаты» (при изучении темы «Площади и объемы» в 5 классе); «Бизнес-план строительства катка» (по теме «Основные задачи на дроби» в 6 классе), «Экскурсионные маршруты по культурным местам Орехова-Зуева» (при изучении темы «Масштаб»).
При применении системно-деятельностного подхода учащиеся ставятся в такие условия, когда сами добывают знания, участвуют в учебных проектах; ставят личные цели для достижения определённого результата.
О каких-либо серьёзных результатах говорить ещё рано, но думаем, что можем говорить о таких метапредметных результатах как понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем; умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
ФГОС. Цели обучения математике в старшей школе. Дифференциация обучения математике.
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
ФГОС. Цели обучения математике в старшей школе. Дифференциация обучения математике.
План лекции: Значения математического образования. Цели обучения математике в старшей школе (действующий Госстандарт). Новый ФГОС
Особенности математического знания изучение не конкретных явлений, предметов, событий реального мира, а достаточно общих и абстрактных моделей этого мира; универсальность математического знания; использование специального универсального языка; логическая строгость и аргументированность основных позиций; структурированность (алгебраические, порядковые, топологические) ; высокий уровень теоретического знания и влияние его на развитие теоретического мышления.
Действующий стандарт В основе лежит Федеральный компонент государственного стандарта общего образования («Вестник образования России», 2004г, №12-14, ст. школа, №14, с. 60-78). Здесь сформулированы три группы целей: Образовательные –овладение ЗУН о науке, её языке, символике; Воспитательные –мировоззрение, логической и эвристической составляющей мышления, алгоритмическим мышлением, самостоятельностью и активностью; Практические – умение строить математические модели, исследовать явления по моделям.
Действующий стандарт. Задачи курса математики В настоящее время задачи курса математики старшей школы: расширение и систематизация общих сведений о функции, изучение новых классов элементарных функций; расширение и систематизация математического аппарата, сформированного в основной школе (выражение, уравнение, неравенства, вычисления, включение новых видов функций); ознакомление с элементами дифференциального и интегрального исчисления как аппаратом исследования функций, решения прикладных задач; изучение свойств пространственных тел, формирование умений применять эти свойства для решения практических задач;
Действующий стандарт. Задачи курса математики расширение и углубление представлений о математике как элементе человеческой культуры, о применении её в практике, в научном познании (осознание универсальности математических понятий, теорий, методов, иллюстрация их применения в реальных областях человеческой деятельности); совершенствование интеллектуальных и речевых умений путём развития логического мышления, обогащение математического языка. Правительство РФ утвердило Концепцию развития математического образования в Российской Федерации специальным распоряжением от 24 декабря 2013 г. №2506-р
ФЕДЕРАЛЬНЫЙ ГОСУДАРСТВЕННЫЙ ОБРАЗОВАТЕЛЬНЫЙ СТАНДАРТ среднего (полного) ОБЩЕГО ОБРАЗОВАНИЯ Проект стандарта разработан Институтом стратегических исследований в образовании Российской академии образования Руководители разработки проекта: Кезина Л.П., академик РАО; Кондаков А.М., научный руководитель ИСИО РАО, член-корреспондент РАО Утверждён приказом Минобрнауки от 17 мая 2012г №413 и вступил в действие со 2июля 2012 г.
Новый ФГОС Теперь ФГОС включает 4 раздела и 3 вида требований: 1) Общие положения; 2) Требования к результатам освоения основной образовательной программы (личностные, метапредметные и предметные); 3) требования к структуре основной образовательной программы (целевой, содержательный и организационный); 4) требования к условиям реализации основной образовательной программы (характеризуют кадровые, финансовые, материально-технические и иные условия реализации основной образовательной программы).
Из раздела «Общие положения»: «Методологической основой Стандарта является системно-деятельностный подход, который обеспечивает: формирование готовности обучающихся к саморазвитию и непрерывному образованию; проектирование и конструирование развивающей образовательной среды образовательного учреждения; активную учебно-познавательную деятельность обучающихся; построение образовательного процесса с учетом индивидуальных, возрастных, психологических, физиологических особенностей и здоровья обучающихся.»
Стандарт устанавливает требования к результатам обучающихся, освоивших основную образовательную программу среднего (полного) общего образования: личностные; метапредметные; предметные
Требования к результатам обучающихся личностным, включающим готовность и способность обучающихся к саморазвитию и личностному самоопределению, сформированность их мотивации к обучению и целенаправленной познавательной деятельности, системы значимых социальных и межличностных отношений, ценностно-смысловых установок, отражающих личностные и гражданские позиции в деятельности, правосознание, способность ставить цели и строить жизненные планы, способность к осознанию российской идентичности в поликультурном социуме;
Требования к результатам обучающихся метапредметным, включающим освоенные обучающимися : межпредметные понятия и универсальные учебные действия (регулятивные, познавательные, коммуникативные), способность их использования в познавательной и социальной практике, самостоятельность в планировании и осуществлении учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками, способность к построению индивидуальной образовательной траектории, владение навыками учебно-исследовательской, проектной и социальной деятельности;
Требования к результатам обучающихся предметным, включающим освоенные обучающимися в ходе изучения учебного предмета умения, специфические для данной предметной области, виды деятельности по получению нового знания в рамках учебного предмета, его преобразованию и применению в учебных, учебно-проектных и социально-проектных ситуациях, формирование научного типа мышления, научных представлений о ключевых теориях, типах и видах отношений, владение научной терминологией, ключевыми понятиями, методами и приёмами.
Метапредметные результаты освоения основной образовательной программы среднего (полного) общего образования должны отражать: 1) умение самостоятельно определять цели и составлять планы; самостоятельно осуществлять, контролировать и корректировать урочную и внеурочную (включая внешкольную) деятельность; использовать различные ресурсы для достижения целей; выбирать успешные стратегии в трудных ситуациях; 2) умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции другого, эффективно разрешать конфликты;
3) владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания; 4) готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников; 5) умение ориентироваться в социально-политических и экономических событиях, оценивать их последствия; Метапредметные результаты
Метапредметные результаты 6) умение самостоятельно оценивать и принимать решения, определяющие стратегию поведения, с учётом гражданских и нравственных ценностей; 7) владение языковыми средствами – умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства; 8) владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения.
Направления специализации При разработке модели обучения математике в условиях профильной дифференциации были взяты следующие направления специализации: Гуманитарное направление, включающее в себя специализированные учебные заведения, школы и классы с углубленным изучением иностранных языков, истории, филологии, философии и т.д. Прикладное направление, ориентированное на использование математике в науке, технике, производстве, экономике и т.д. Естественнонаучное направление, включающее в себя физико-математические школы и классы. В настоящее время в Стандарте они преобразованы в базовый курс и углублённый уровень.
Предметные результаты. Математика и информатика. Изучение предметной области «Математика и информатика» должно обеспечить: сформированность представлений о социальных, культурных и исторических факторах становления математики и информатики; сформированность основ логического, алгоритмического и математического мышления; сформированность умений применять полученные знания при решении различных задач; сформированность представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления;
Предметные результаты сформированность представлений о роли информатики и ИКТ в современном обществе, понимание основ правовых аспектов использования компьютерных программ и работы в Интернете; сформированность представлений о влиянии информационных технологий на жизнь человека в обществе; понимание социального, экономического, политического, культурного, юридического, природного, эргономического, медицинского и физиологического контекстов информационных технологий; принятие этических аспектов информационных технологий; осознание ответственности людей, вовлечённых в создание и использование информационных систем, распространение информации.
Математика и информатика (интегрированный курс) Был в проекте ФГОСа, но сейчас отсутствует.
Математика: алгебра и начала математического анализа, геометрия (базовый курс) – требования к предметным результатам должны отражать: 1) сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира; 2) сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий; 3) владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
Математика: алгебра и начала математического анализа, геометрия 4) владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств; 5) сформированность представлений об основных понятиях, идеях и методах математического анализа; 6) владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
Математика: алгебра и начала математического анализа, геометрия 7) сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин; 8) владение навыками использования готовых компьютерных программ при решении задач.
Математика: алгебра и начала математического анализа, геометрия (углублённый уровень) требования к предметным результатам освоения углублённого уровня математики должны включать требования к результатам освоения базового курса и дополнительно отражать: 1) сформированность представлений о необходимости доказательств при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений; 2) сформированность понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;
Математика: алгебра и начала математического анализа, геометрия (углублённый уровень) 3) сформированность умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат; 4) сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей; 5) владение умениями составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с применением формул комбинаторики и основных теорем теории вероятностей; исследования случайных величин по их распределению.
Требования Стандарта к результатам освоения основной образовательной программы определяют содержательно-критериальную и нормативную основу оценки результатов освоения обучающимися основной образовательной программы, деятельности педагогических работников, образовательных учреждений. Освоение обучающимися основной образовательной программы завершается обязательной государственной (итоговой) аттестацией выпускников. Государственная (итоговая) аттестация обучающихся проводится по всем изучавшимся учебным предметам.
Государственная (итоговая) аттестация обучающихся, освоивших основную образовательную программу, проводится в форме единого государственного экзамена по окончании 11 класса в обязательном порядке по учебным предметам: «Русский язык и литература»; «Математика: алгебра и начала анализа, геометрия»; «Иностранный язык». Обучающийся может самостоятельно выбрать уровень (базовый или углубленный), в соответствии с которым будет проводиться государственная (итоговая) аттестация в форме единого государственного экзамена.
Требования к структуре основной образовательной программы Основная образовательная программа определяет цели, задачи, планируемые результаты, содержание и организацию образовательного процесса на ступени среднего (полного) общего образования и реализуется образовательным учреждением через урочную и внеурочную деятельность с соблюдением требований государственных санитарно-эпидемиологических правил и нормативов5.
Требования к структуре основной образовательной программы Внеурочная деятельность организуется по направлениям развития личности (духовно-нравственное, спортивно-оздоровительное, социальное, общеинтеллектуальное, общекультурное) в таких формах, как художественные студии, спортивные клубы и секции, юношеские организации, краеведческая работа, научно-практические конференции, школьные научные общества, олимпиады, поисковые и научные исследования, общественно полезные практики, военно-патриотические объединения и в других формах, отличных от урочной, на добровольной основе в соответствии с выбором участников образовательного процесса. Формы организации образовательного процесса, чередование урочной и внеурочной деятельности в рамках реализации основной образовательной программы определяет образовательное учреждение.
Основная образовательная программа Основная образовательная программа должна содержать три раздела: целевой, содержательный и организационный. Целевой раздел должен определять общее назначение, цели, задачи, планируемые результаты реализации основной образовательной программы, а также способы определения достижения этих целей и результатов и включать: пояснительную записку; планируемые результаты освоения обучающимися основной образовательной программы; систему оценки результатов освоения основной образовательной программы.
Основная образовательная программа Содержательный раздел должен определять общее содержание среднего (полного) общего образования и включать образовательные программы, ориентированные на достижение личностных, предметных и метапредметных результатов, в том числе: программу развития универсальных учебных действий на ступени среднего (полного) общего образования, включающую формирование компетенций обучающихся в области учебно-исследовательской и проектной деятельности; программы отдельных учебных предметов, курсов и курсов внеурочной деятельности;
Основная образовательная программа программу воспитания и социализации обучающихся на ступени среднего (полного) общего образования, включающую такие направления, как духовно-нравственное развитие, воспитание обучающихся, их социализацию и профессиональную ориентацию, формирование экологической культуры, культуры здорового и безопасного образа жизни; программу коррекционной работы, включающую организацию работы с обучающимися с ограниченными возможностями здоровья и инвалидами.
Основная образовательная программа Организационный раздел должен определять общие рамки организации образовательного процесса, а также механизмы реализации основной образовательной программы. Организационный раздел должен включать: учебный план среднего (полного) общего образования как один из основных механизмов реализации основной образовательной программы; план внеурочной деятельности; систему условий реализации основной образовательной программы в соответствии с требованиями Стандарта.
Программы отдельных учебных предметов, курсов должны содержать: 1) пояснительную записку, в которой конкретизируются общие цели среднего (полного) общего образования с учётом специфики учебного предмета; 2) общую характеристику учебного предмета, курса; 3) описание места учебного предмета, курса в учебном плане; 4) личностные, метапредметные и предметные результаты освоения конкретного учебного предмета, курса; 5) содержание учебного предмета, курса; 6) тематическое планирование с определением основных видов учебной деятельности обучающихся; 7) описание учебно-методического и материально-технического обеспечения образовательного процесса.
Требования к условиям реализации основной образовательной программы содержит требования о создании условий для реализации образования, требования к педагогическим кадрам; систему подушевого финансирования; требования санитарно-технические, к информационной среде, к учебно-методическому обеспечению и т.д.
Тема практического занятия: Профильное обучение математике. Основное содержание курса математики на каждом направлении профилизации Профильное обучения, его значения и цели. Организация профильного обучения. Профильное обучение математике. а) базовый уровень б) профильный уровень в) элективные курсы 4) Содержание программы по математике в профильной школе. а) базовый уровень б) гуманитарное направление профилизации в)социально- экономическое направление профилизации г) естественнонаучное направление профилизации д) математический профиль.
