Ускорение автомобиля равно а 4 м с2 что это означает

Ускорение при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Ускорение, разгон, инерция. Автомобиль набирает скорость

Красный свет светофора сменился желтым, затем зеленым. С напряженным ревом срываются с места машины, затем звук двигателей на мгновение стихает — это водители отпустили педаль подачи топлива и переключают передачи, снова разгон, снова момент затишья и опять разгон. Только метров через 100 после перекрестка поток машин как бы успокаивается и плавно катит до следующего светофора. Лишь один старый автомобиль «Москвич» прошел перекресток ровно и бесшумно. На рисунке видно, как он обогнал все автомобили и вырвался далеко вперед. Этот автомобиль подъехал к перекрестку как раз в тот момент, когда зажегся зеленый сигнал светофора, водителю не пришлось тормозить и останавливать машину, не пришлось после этого снова брать разгон. Как же получается, что один автомобиль (да еще маломощный «Москвич» старого выпуска) легко, без напряжения движется со скоростью около 50 км/час, в то время как другие с явным напряжением постепенно набирают скорость и достигают скорости 50 км/час далеко после перекрестка, когда «Москвич» уже приближается к следующему светофору? Очевидно, что для равномерного движения требуется значительно меньше усилий и расхода мощности, чем при разгоне или, как говорят, при ускоренном движении.

Рис. Сравнительно слабый автомобиль может обогнать более мощные, если он подходит к перекрестку в момент включения зеленого света и не затрачивает усилий на трогание с места и разгон.

Но прежде чем изучать разгон автомобиля, нужно вспомнить некоторые понятия.

Ускорение автомобиля

Если автомобиль проходит в каждую секунду одинаковое число метров, движение называется равномерным или установившимся. Если пройденный автомобилем путь в каждую секунду (скорость) изменяется, движение называется:

Приращение скорости в единицу времени называют ускорением, уменьшение скорости в единицу времени — отрицательным ускорением, или замедлением.

Ускорение измеряют приростом или убыванием скорости (в метрах в секунду) за 1 сек. Если за секунду скорость увеличивается на 3 м/сек, ускорение равно 3 м/сек в секунду или 3 м/сек/сек или 3 м/сек2.

Ускорение обозначают буквой j.

Ускорение, равное 9,81 м/сек2 (или округленно, 10 м/сек2), соответствует ускорению, которое, как известно из опыта, имеет свободно падающее тело (без учета сопротивления воздуха), и называется ускорением силы тяжести. Его обозначают буквой g.

Разгон автомобиля

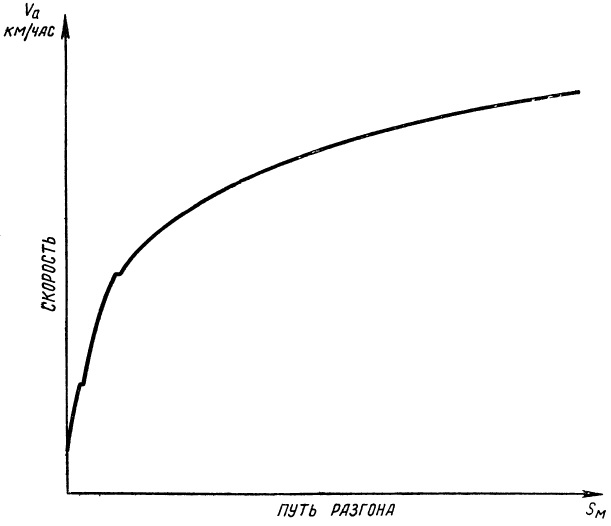
Разгон автомобиля обычно изображают графически. На горизонтальной оси графика откладывают путь, а на вертикальной — скорость и наносят точки, соответствующие каждому пройденному отрезку пути. Вместо скорости на вертикальной шкале можно откладывать время разгона, как это показано на графике разгона отечественных автомобилей.

График разгона представляет собой кривую с постепенно убывающим углом наклона. Уступы кривой соответствуют моментам переключения передач, когда ускорение на какой-то момент падает, однако их часто не показывают.

Инерция

Автомобиль не может с места развить сразу большую скорость, потому что ему приходится преодолевать не только силы сопротивления движению, но и инерцию.

Инерция — это свойство тела сохранять состояние покоя или состояние равномерного движения. Из механики известно, что неподвижное тело может быть приведено в движение (или скорость движущегося тела изменена) только под действием внешней силы. Преодолевая действие инерции, внешняя сила изменяет скорость тела, иначе говоря, придает ему ускорение. Величина ускорения пропорциональна величине силы. Чем больше масса тела, тем большей должна быть сила для придания этому телу нужного ускорения. Масса — это величина, пропорциональная количеству вещества в теле; масса т равна весу тела G, деленному на ускорение силы тяжести g (9,81 м/сек2):

Масса автомобиля сопротивляется разгону с силой Pj, эту силу называют силой инерции. Чтобы разгон мог произойти, на ведущих колесах нужно создать дополнительно силу тяги, равную силе инерции. Значит, сила, необходимая для преодоления инерции тела и для придания телу определенного ускорения j, оказывается пропорциональной массе тела и ускорению. Эта сила равна:

Для ускоренного движения автомобиля требуется дополнительная затрата мощности:

Nj = Pj*Va / 75 = Gj*Va / 270*9,81 = Gj*Va / 2650, л.с.

Для точности расчетов в уравнения (31) и (32) следует включить множитель б («дельта») — коэффициент вращающихся масс, учитывающий влияние вращающихся масс автомобиля (особенно маховика двигателя и колес) на разгон. Тогда:

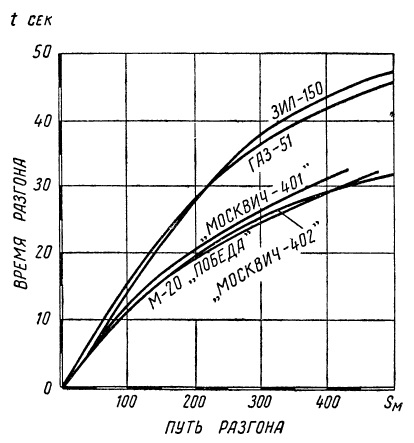
Рис. Графики времени разгона отечественных автомобилей.

Влияние вращающихся масс заключается в том, что, кроме преодоления инерции массы автомобиля, необходимо «раскрутить» маховик, колеса и другие вращающиеся части машины, затратив на это часть мощности двигателя. Величину коэффициента б можно считать приблизительно равной:

где ik — передаточное число в коробке передач.

Теперь, взяв для примера автомобиль с полным весом 2000 кг, нетрудно сравнить силы, необходимые для поддержания движения этого автомобиля по асфальту со скоростью 50 км/час (пока без учета сопротивления воздуха) и для трогания его с места с ускорением около 2,5 м/сек2, обычным для современных легковых автомобилей.

Для преодоления сопротивления инерции на высшей передаче (ik = 1) потребуется сила:

Такой силы на высшей передаче автомобиль не может развить, нужно включить первую передачу (с передаточным числом ik = 3).

Pj = 2000*2,5*1,5 / 9,81 = 760, кг

что для современных легковых автомобилей вполне возможно.

Итак, сила, необходимая для трогания с места, оказывается в 25 раз больше силы, необходимой для поддержания движения с постоянной скоростью 50 км/час.

Чтобы обеспечить быстрый разгон автомобиля, требуется устанавливать двигатель большой мощности. При движении с постоянной скоростью (кроме максимальной) двигатель работает не в полную мощность.

Из сказанного выше понятно, почему при трогании с места нужно включать низшую передачу. Попутно отметим, что на грузовых автомобилях обычно следует начинать разгон на второй передаче. Дело в том, что на первой передаче (ik примерно равно 7.) очень велико влияние вращающихся масс и тяговой силы не хватит, чтобы сообщить автомобилю большое ускорение; разгон получится очень медленным.

На сухой дороге при коэффициенте сцепления ф, равном около 0,7, трогание с места на низшей передаче не вызывает никаких затруднений, так как сила сцепления все еще превышает тяговую силу. Но на скользкой дороге может часто оказаться, что тяговая сила на низшей передаче больше силы сцепления (особенно при ненагруженном автомобиле), и колеса начинают буксовать. Из этого положения есть два выхода:

При разгоне особенно сказывается разгрузка передних колес и дополнительная нагрузка задних. Можно наблюдать, как в момент трогания с места автомобиль заметно, а иногда и очень резко «приседает» на задние колеса. Это перераспределение нагрузки происходит и при равномерном движении автомобиля. Оно объясняется противодействием вращающему моменту. Зубья ведущей шестерни главной передачи давят на зубья ведомой (коронной) и как бы прижимают заднюю ось к земле; при этом возникает реакция, отталкивающая ведущую шестерню вверх; происходит небольшое поворачивание всего заднего моста в направлении, обратном направлению вращения колес. Закрепленные на картере моста рессоры своими концами приподнимают переднюю часть рамы или кузова и опускают заднюю. Между прочим отметим, что именно вследствие разгрузки передних колес их легче повернуть во время движения автомобиля с включенной передачей, чем во время движения накатом, а тем более чем на стоянке. Это знает каждый водитель. Однако вернемся к дополнительно нагруженным задним колесам.

Дополнительная, прибавочная нагрузка на задние колеса Zd от передаваемого момента тем больше, чем больше момент Мк, подведенный к колесу и чем короче колесная база автомобиля L (в м):

Естественно, что эта нагрузка особенно велика при движении на низших передачах, так как подводимый к колесам момент увеличен. Так, на автомобиле ГАЗ-51 дополнительная нагрузка на первой передаче равна:

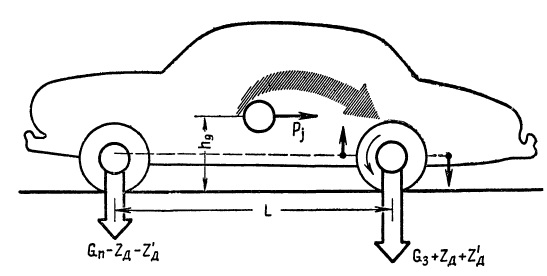
Во время трогания с места и разгона на автомобиль действует сила инерции Pj, приложенная в центре тяжести автомобиля и направленная назад, т. е. в сторону, обратную ускорению. Так как сила Pj приложена на высоте hg от плоскости дороги, она будет стремиться как бы опрокинуть автомобиль вокруг задних колес. При этом нагрузка на задние колеса увеличится, а на передние — уменьшится на величину:

Рис. При передаче усилий от двигателя нагрузка на задние колеса увеличивается, а на передние — уменьшается.

Таким образом, при трогании с места на задние колеса и шины приходится нагрузка от веса автомобиля, от передаваемого увеличенного вращающего момента и от силы инерции. Эта нагрузка действует на подшипники заднего моста и главным образом на шины задних колес. Чтобы сберечь их, нужно троганье с места осуществлять как можно более плавно. Следует напомнить, что на подъеме задние колеса еще более нагружены. На крутом подъеме при трогании с места, да еще при высоком расположении центра тяжести автомобиля, может создаться такая разгрузка передних колес и перегрузка задних, которая приведет к повреждению шин и даже к опрокидыванию автомобиля назад.

Рис. Кроме нагрузки от тягового усилия, при разгоне на задние колеса действует дополнительная сила от инерции массы автомобиля.

Автомобиль двигается с ускорением, и скорость движения его увеличивается, пока тяговая сила больше силы сопротивления движению. С увеличением скорости сопротивление движению возрастает; когда установится равенство тяговой силы и сопротивления, автомобиль приобретает равномерное движение, скорость которого зависит от величины нажима на педаль подачи топлива. Если водитель до отказа нажимает на педаль подачи топлива, эта скорость равномерного движения является одновременно и наибольшей скоростью автомобиля.

Работа по преодолению сил сопротивления качению и воздуха не создает запаса энергии — энергия расходуется на борьбу с этими силами. Работа по преодолению сил инерции при разгоне автомобиля переходит в энергию движения. Эту энергию называют кинетической энергией. Создающийся при этом запас энергии можно использовать, если после некоторого разгона отсоединить ведущие колеса от двигателя, установить рычаг переключения коробки передач в нейтральное положение, т. е. дать возможность автомобилю двигаться по инерции, накатом. Движение накатом происходит до тех пор, пока запас энергии не израсходуется на преодоление сил сопротивления движению. Уместно напомнить, что на одном и том же отрезке пути расход энергии на разгон гораздо больше расхода на преодоление сил сопротивления движению. Поэтому за счет накопленной энергии путь наката может быть в несколько раз больше пути разгона. Так, путь наката со скорости 50 км/час равен для автомобиля «Победа» около 450 м, для автомобиля ГАЗ-51 — около 720 м, в то время как путь разгона до этой скорости равен соответственно 150—200 м и 250—300 м Если водитель не стремится ехать на автомобиле с очень большой скоростью, он может значительную часть пути вести автомобиль «накатом» и экономить таким образом энергию и, тем самым, топливо.

Источник

Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Теперь мы можем выделить кинематические характеристики движения тела:

Перемещение тела определяется формулой:

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

Кинетическая энергия тела определяется формулой:

Скорость при прямолинейном равноускоренном движении равна:

v = v 0 + a t = 5 − 6 t

Поэтому кинетическая энергия тела равна:

Следовательно, правильная последовательность цифр в ответе будет: 34.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник