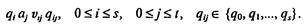В машине тьюринга предписание r для лентопротяжного механизма означает
Тест по курсу «Теория алгоритмов» Специальность «Информатика и вычислительная техника»
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Тест по курсу «Теория алгоритмов»
Специальность «Информатика и вычислительная техника»
1. Как называется графическое представление алгоритма: 1) последовательность формул; 2) блок-схема; 3) таблица; 4) словесное описание?
2. На рисунке представлена часть блок-схемы. Как называется такая вершина:
1) предикатная; 2) объединяющая; 3) функциональная; 4) сквозная?
3. На рисунке представлена часть блок-схемы. Как называется такая вершина:
4. На рисунке представлена часть блок-схемы. Как она называется:
5. На рисунке представлена часть блок-схем Как она называется:
цикл с предусловием;
6. На рисунке представлена часть блок-схемы.
Как она называется:
цикл с предусловием;
цикл с постусловием?
7. На рисунке представлена часть блок-схемы.Как она называется:
цикл с постусловием;
цикл с предусловием?
8. Как называется конструкция блок-схемы, изображенная на рисунке:
вызов вспомогательного алгоритма;
9. Как называется конструкция блок-схемы, изображенная на рисунке:
вызов вспомогательного алгоритма;
10. Как называется конструкция блок-схемы, изоб
раженная на рисунке:
вызов вспомогательного алгоритма;
11. Как называется конструкция блок-схемы, изображенная на рисунке:
вызов вспомогательного алгоритма;
12. Свойство алгоритма записываться в виде упорядоченной совокупности отделенных друг от друга предписаний (директив):
1) понятность; 2) определенность; 3) дискретность; 4) массовость.
13. Свойство алгоритма записываться в виде только тех команд, которые находятся в Системе Команд Исполнителя, называется:
1) понятность; 2) определенность; 3) дискретность; 4) результативность.
14. Свойство алгоритма записываться только директивами однозначно и одинаково интерпретируемыми разными исполнителями:
1) дискретность; 2) понятность3) определенность; 4) результативность
15. Свойство алгоритма, что при точном исполнении всех предписаний процессдолжен прекратиться за конечное число шагов с определенным ответом на поставленную задачу:
1) понятность; 2) детерминированность; 3) дискретность; 4) результативность.
16. Свойство алгоритма обеспечения решения не одной задачи, а целого класса
задач этого типа:
1) понятность; 2) определенность; 3) дискретность; 4) массовость.
17. Что называют служебными словами в алгоритмическом языке:
слова, употребляемые для записи команд, входящих в СКИ;
слова, смысл и способ употребления которых задан раз и навсегда;
вспомогательные алгоритмы, которые используются в составе других алгоритмов;
константы с постоянным значением?
18. Рекурсия в алгоритме будет прямой, когда:
рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.
19. Рекурсия в алгоритме будет косвенной, когда: алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.
п — действие, выполняемое головкой; К— номер следующей команды, подлежащей выполнению; т — порядковый номер команды;
п — порядковый номер команды; К — действие, выполняемое головкой; т — номер следующей команды, подлежащей выполнению;
п — порядковый номер команды; К— номер следующей команды, подлежащей выполнению; т — действие, выполняемое головкой;
п — порядковый номер команды; К — действие, выполняемое головкой; т — номер клетки, с которой данную команду надо произвести.
Сколько существует команд у машины Поста:
В машине Поста останов будет результативным:
при выполнении недопустимой команды;
если машина не останавливается никогда;
если результат выполнения программы такой, какой и ожидался;
23. В машине Поста некорректным алгоритм будет в следующем случае:
при выполнении недопустимой команды;
результат выполнения программы такой, какой и ожидался;
машина не останавливается никогда;
24. В машине Тьюринга рабочий алфавит:
25. В машине Тьюринга состояниями являются:
26. В машине Тьюринга предписание L для лентопротяжного механизма означает:1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
27. В машине Тьюринга предписание R для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
28. В машине Тьюринга предписание S для лентопротяжного механизма означает:1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
29. В алгоритме Маркова ассоциативным исчислением называется:
совокупность всех слов в данном алфавите;
совокупность всех допустимых систем подстановок;
совокупность всех слов в данном алфавите вместе с допустимой системой подстановок;
когда все слова в алфавите являются смежными.
30. В ассоциативном счислении два слова называются смежными:
если одно из них может быть преобразовано в другое применением подстановок;
если одно из них может быть преобразовано в другое однократным применением допустимой подстановки;
когда существует цепочка от одного слова к другому и обратно;
когда они дедуктивны.
смежные, то цепочка называется:
33. В алгоритмах Маркова дана система подстановок в алфавите Л = <а, Ь, с>:
abc — с
34. В алгоритмах Маркова дана система подстановок в алфавите А = <а, Ь, с>:
cb — abc
35. Способ композиции нормальных алгоритмов будет суперпозицией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся i
пересечении областей определения алгоритмов А и В;
существует алгоритм С, являющийся суперпозицией алгоритмов А и Д
такой, что для любого входного слова р С<р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
36. Способ композиции нормальных алгоритмов будет объединением, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
существует алгоритм С, являющийся суперпозицией алгоритмов А и Д
такой, что для любого входного слова р С(р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
37. Способ композиции нормальных алгоритмов будет разветвлением, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В,
такой, что для любого входного слова р С<р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
38. Способ композиции нормальных алгоритмов будет итерацией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
Свойство алгоритма записываться в виде упорядоченной совокупности отделенных друг от друга предписаний (директив):
понятность; 2) определенность; 3) дискретность; 4) массовость.
Свойство алгоритма записываться в виде только тех команд, которые находятся в Системе Команд Исполнителя, называется:
1) понятность; 2)определенность; 3) дискретность; 4) результативность.
Свойство алгоритма записываться только директивами однозначно и одинаково интерпретируемыми разными исполнителями:
1) детерминированность; 2) результативность; 3) дискретность; 4) понятность.
Свойство алгоритма, что при точном исполнении всех предписаний процесс должен прекратиться за конечное число шагов с определенным ответом на поставленную задачу:
1) детерминированность; 2) результативность; 3) дискретность; 4) понятность.
Свойство алгоритма обеспечения решения не одной задачи, а целого класса задач этого типа; 1) понятность; 2) детерминированность; 3) дискретность; 4) массовость.
Что называют служебными словами в алгоритмическом языке:
слова, употребляемые для записи команд, входящих в СКИ;
слова, смысл и способ употребления которых задан раз и навсегда;
вспомогательные алгоритмы, которые используются в составе других алгоритмов;
константы с постоянным значением?
Рекурсия в алгоритме будет прямой, когда:
рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.
Рекурсия в алгоритме будет косвенной, когда:
рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.
Команда машины Поста имеет структуру п Km, где:
n — порядковый номер команды; К— действие, выполняемое головкой; m — номер клетки, с которой данную команду надо произвести.
Сколько существует команд у машины Поста: 1) 2; 2) 4; 3) 6; 4) 8?
В машине Поста останов будет результативным:
при выполнении недопустимой команды;
если машина не останавливается никогда;
если результат выполнения программы такой, какой и ожидался;
В машине Поста некорректным алгоритм будет в следующем случае:
при выполнении недопустимой команды;
результат выполнения программы такой, какой и ожидался;
машина не останавливается никогда;
В машине Тьюринга рабочий алфавит:
В машине Тьюринга состояниями являются:
В машине Тьюринга предписание L для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево; 3) остановить машину;
4) занести в ячейку символ.
В машине Тьюринга предписание R для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево; 3) остановить машину;
4) занести в ячейку символ.
В машине Тьюринга предписание S для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
В алгоритме Маркова ассоциативным исчислением называется:
совокупность всех слов в данном алфавите;
совокупность всех допустимых систем подстановок;
совокупность всех слов в данном алфавите вместе с допустимой системой подстановок;
когда все слова в алфавите являются смежными.
В ассоциативном счислении два слова называются смежными:
если одно из них может быть преобразовано в другое применением подстановок;
если одно из них может быть преобразовано в другое однократным применением допустимой подстановки;
когда существует цепочка от одного слова к другому и обратно;
когда они дедуктивны.
ассоциативной; 2) эквивалентной; 3) индуктивной; 4) дедуктивной.
ассоциативными; 2) эквивалентными; 3) индуктивными; 4) дедуктивными.
В алгоритмах Маркова дана система подстановок в алфавите А = <а, b, с>:
abc — с; ba — cb; са — аb.
Преобразуйте с помощью этой системы слово bacaabc:
1) cbc; 2) ccbcbbc; 3) cbacba; 4) cbabc.
В алгоритмах Маркова дана система подстановок в алфавите А = <а, b, с>:
cb — abс; bac — ac; саb — b.
Преобразуйте с помощью этой системы слово bcabacab:
1) ccb; 2) cab; 3) cbc; 4) bcaab.
Способ композиции нормальных алгоритмов будет суперпозицией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;
алгоритм D будет суперпозицией трех алгоритмов А В С, причем область определения D является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения D(p)=A(p), если С(р) = е, D(p) = В(р), если С(р) = е, где е — пустая строка;
существует алгоритм С, являющийся суперпозицией алгоритмов А и B такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
Способ композиции нормальных алгоритмов будет объединением, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;
алгоритм D будет суперпозицией трех алгоритмов А В С, причем область определения D является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения D(p) = A(p), если С(р) = е, D(p) = В(р), если С(р) = е, где е — пустая строка;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
Способ композиции нормальных алгоритмов будет разветвлением, если:
1) выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;
алгоритм D будет суперпозицией трех алгоритмов A B C, причем область определения D является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения D(p) = А(р), если С(р) = е, D(p) — В(р), если С(р) = е, где е — пустая строка;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
Способ композиции нормальных алгоритмов будет итерацией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;
алгоритм D будет суперпозицией трех алгоритмов A B C, причем область определения D является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения
D(p) = А(р), если С(р) = е, D(p) — В(р), если С(р) = е, где е — пустая строка;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
МАШИНА ТЬЮРИНГА



Машина Тьюринга подобна машине Поста, но функционирует несколько иначе.
Порядок работы МТ (с рабочим алфавитом a0, a1. аt и состояниями q0, q1. qs) описывается таблицей машины Тьюринга. Эта таблица является матрицей с четырьмя столбцами и (s + 1) (t + 1) строками. Каждая строка имеет вид
Машина Тьюринга начинает работу из некоторой начальной конфигурации, включающей в себя начальное состояние (обычно q0) и положение считывающе-записывающей головки над определенной ячейкой ленты, содержащей один из символов рабочего алфавита A.
Отметим, что наличие разнообразных символов в рабочем алфавите МТ позволяет представлять на ленте произвольную текстовую и числовую информацию, а переходы управляющего центра МТ в различные состояния моделируют запоминание машиной Тьюринга промежуточных результатов работы. Таблица, определяющая порядок работы МТ, не является в прямом смысле слова программой (ее предписания выполняются не последовательно, одно за другим, а описывают преобразования символов некоторого текста, находящегося на ленте). Таблицу МТ часто называют схемой машины Тьюринга или попросту отождествляют с самой машиной Тьюринга, коль скоро ее устройство и принцип функционирования известны.
Рассмотрим примеры нескольких схем машины Тьюринга.
1. Алгоритм прибавления единицы к числу п в десятичной системе счисления. Дана десятичная запись числа п (т.е. представление натурального числа п в десятичной системе счисления); требуется получить десятичную запись числа п + 1.
Очевидно, что внешний алфавит МТ должен состоять из десяти цифр 0,1,2,3,4,5,6,7,8,9 и символа пробела _. Эти цифры записывают по одной в ячейке (подряд, без пропусков).
Оказывается достаточным иметь два внутренних состояния машины: q1 и q2.
Предположим, что в начальный момент головка находится над одной из цифр числа, а машина находится в состоянии q1. Тогда задача может быть решена в два этапа: движения головки к цифре единиц числа (во внутреннем состоянии q1) и замене этой цифры на единицу большую (с учетом переноса 1 в следующий разряд, если это 9, во внутреннем состоянии q2. Соответствующая схема МТ может иметь вид
| аi | qi | |
| q1 | q2 | |
| 0Пq1 | 1Cq2 | |
| 1Пq1 | 2Cq2 | |
| 2Пq1 | 3Cq2 | |
| 3Пq1 | 4Cq2 | |
| 4Пq1 | 5Cq2 | |
| 5Пq1 | 6Cq2 | |
| 6Пq1 | 7Cq2 | |
| 7Пq1 | 8Cq2 | |
| 8Пq1 | 9Cq2 | |
| 9Пq1 | 0Cq2 | |
| — | -Лq1 | 1Cq2 |
2. Алгоритм записи числа в десятичной системе счисления.
Дана конечная последовательность меток, записанных в клетки ленты подряд, без пропусков. Требуется записать в десятичной системе число этих меток пересчитать метки).
Суть алгоритма может состоять в том, что к числу 0, записанному на ленте в начале работы машины, машина добавляет 1, стирая метку за меткой, так что вместо нуля возникает число 0 + k.
Легко могут быть построены алгоритмы сложения чисел, их перемножения, нападения наибольшего общего делителя и т.д. Однако, главная цель введения машин Поста и Тьюринга не программирование для них, а изучение свойств алгоритмов и проблемы алгоритмической разрешимости задач.
В зависимости от числа используемых лент, их назначения и числа состояний устройства управления можно рассматривать различные модификации машин Тьюринга.
До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако, можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм любой машины Тьюринга. Это достигается путем кодирования конфигурации и программы любой данной машины Тьюринга в символах внешнего алфавита универсальной машины. Само кодирование должно выполняться следующим образом:
1) различные символы должны заменяться различными кодовыми группами, но один и тот же символ должен заменяться всюду, где бы он не встретился, одной и той же кодовой группой;
2) строки кодовых записей должны однозначно разбиваться на отдельные кодовые группы;
3) должна иметься возможность распознать кодовые группы, соответствующие командам Л, П, С, различать кодовые группы, соответствующие символам внешнего алфавита и внутренним состояниям.
Для сравнения структур различных машин и оценки их сложности необходимо иметь соответствующую меру сложности машин. К.Шеннон предложил рассматривать в качестве такой меры произведение числа символов внешнего алфавита и числа внутренних состояний. Большой интерес вызывает задача построения универсальной машин Тьюринга наименьшей сложности.
Таким же образом определяется операция возведения в степень: n-й степенью машины Т называется произведение T. Т c n сомножителями.
Операция итерации применима к одной машине и определяется следующим образом. Пусть машина T1 имеет несколько заключительных состояний. Выберем ее r-е заключительное состояние и отождествим его в схеме машины с ее начальным состоянием. Полученная машина T является результатом итерации машины Т1 : Т = T1.
Прежде чем остановиться на проблеме алгоритмической разрешимости задач обратимся к другим способам формализации понятия алгоритма.
Тест по курсу «теория алгоритмов»
Тест по курсу «Теория алгоритмов»
1. Как называется графическое представление алгоритма: 1) последовательность формул; 2) блок-схема; 3) таблица; 4) словесное описание?
2. На рисунке представлена часть блок-схемы. Как называется такая вершина:
1) предикатная; 2) объединяющая; 3) функциональная; 4) сквозная?
3. На рисунке представлена часть блок-схемы. Как называется такая вершина:
4. На рисунке представлена часть блок-схемы. Как она называется:
5. На рисунке представлена часть блок-схем Как она называется:
цикл с предусловием;
6. На рисунке представлена часть блок-схемы.
Как она называется:
цикл с предусловием;
цикл с постусловием?
7. На рисунке представлена часть блок-схемы.Как она называется:
цикл с постусловием;
цикл с предусловием?
8. Как называется конструкция блок-схемы, изображенная на рисунке:
вызов вспомогательного алгоритма;
9. Как называется конструкция блок-схемы, изображенная на рисунке:
вызов вспомогательного алгоритма;
10. Как называется конструкция блок-схемы, изоб
раженная на рисунке:
вызов вспомогательного алгоритма;
11. Как называется конструкция блок-схемы, изображенная на рисунке:
вызов вспомогательного алгоритма;
12. Свойство алгоритма записываться в виде упорядоченной совокупности отделенных друг от друга предписаний (директив):
1) понятность; 2) определенность; 3) дискретность; 4) массовость.
13. Свойство алгоритма записываться в виде только тех команд, которые находятся в Системе Команд Исполнителя, называется:
1) понятность; 2) определенность; 3) дискретность; 4) результативность.
14. Свойство алгоритма записываться только директивами однозначно и одинаково интерпретируемыми разными исполнителями:
1) дискретность; 2) понятность3) определенность; 4) результативность
15. Свойство алгоритма, что при точном исполнении всех предписаний процессдолжен прекратиться за конечное число шагов с определенным ответом на поставленную задачу:
1) понятность; 2) детерминированность; 3) дискретность; 4) результативность.
16. Свойство алгоритма обеспечения решения не одной задачи, а целого класса
задач этого типа:
1) понятность; 2) определенность; 3) дискретность; 4) массовость.
17. Что называют служебными словами в алгоритмическом языке:
слова, употребляемые для записи команд, входящих в СКИ;
слова, смысл и способ употребления которых задан раз и навсегда;
вспомогательные алгоритмы, которые используются в составе других алгоритмов;
константы с постоянным значением?
18. Рекурсия в алгоритме будет прямой, когда:
рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.
19. Рекурсия в алгоритме будет косвенной, когда: алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.
п — действие, выполняемое головкой; К— номер следующей команды, подлежащей выполнению; т — порядковый номер команды;
п — порядковый номер команды; К — действие, выполняемое головкой; т — номер следующей команды, подлежащей выполнению;
п — порядковый номер команды; К— номер следующей команды, подлежащей выполнению; т — действие, выполняемое головкой;
п — порядковый номер команды; К — действие, выполняемое головкой; т — номер клетки, с которой данную команду надо произвести.
Сколько существует команд у машины Поста:
В машине Поста останов будет результативным:
при выполнении недопустимой команды;
если машина не останавливается никогда;
если результат выполнения программы такой, какой и ожидался;
23. В машине Поста некорректным алгоритм будет в следующем случае:
при выполнении недопустимой команды;
результат выполнения программы такой, какой и ожидался;
машина не останавливается никогда;
24. В машине Тьюринга рабочий алфавит:
25. В машине Тьюринга состояниями являются:
26. В машине Тьюринга предписание L для лентопротяжного механизма означает:1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
27. В машине Тьюринга предписание R для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
28. В машине Тьюринга предписание S для лентопротяжного механизма означает:1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
29. В алгоритме Маркова ассоциативным исчислением называется:
совокупность всех слов в данном алфавите;
совокупность всех допустимых систем подстановок;
совокупность всех слов в данном алфавите вместе с допустимой системой подстановок;
когда все слова в алфавите являются смежными.
30. В ассоциативном счислении два слова называются смежными:
если одно из них может быть преобразовано в другое применением подстановок;
если одно из них может быть преобразовано в другое однократным применением допустимой подстановки;
когда существует цепочка от одного слова к другому и обратно;
когда они дедуктивны.
смежные, то цепочка называется:
33. В алгоритмах Маркова дана система подстановок в алфавите Л = <а, Ь, с>:
abc — с
34. В алгоритмах Маркова дана система подстановок в алфавите А = <а, Ь, с>:
cb — abc
35. Способ композиции нормальных алгоритмов будет суперпозицией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся i
пересечении областей определения алгоритмов А и В;
существует алгоритм С, являющийся суперпозицией алгоритмов А и Д
такой, что для любого входного слова р С<р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
36. Способ композиции нормальных алгоритмов будет объединением, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
существует алгоритм С, являющийся суперпозицией алгоритмов А и Д
такой, что для любого входного слова р С(р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
37. Способ композиции нормальных алгоритмов будет разветвлением, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В,
такой, что для любого входного слова р С<р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
38. Способ композиции нормальных алгоритмов будет итерацией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
Свойство алгоритма записываться в виде упорядоченной совокупности отделенных друг от друга предписаний (директив):
понятность; 2) определенность; 3) дискретность; 4) массовость.
Свойство алгоритма записываться в виде только тех команд, которые находятся в Системе Команд Исполнителя, называется:
1) понятность; 2)определенность; 3) дискретность; 4) результативность.
Свойство алгоритма записываться только директивами однозначно и одинаково интерпретируемыми разными исполнителями:
1) детерминированность; 2) результативность; 3) дискретность; 4) понятность.
Свойство алгоритма, что при точном исполнении всех предписаний процесс должен прекратиться за конечное число шагов с определенным ответом на поставленную задачу:
1) детерминированность; 2) результативность; 3) дискретность; 4) понятность.
Свойство алгоритма обеспечения решения не одной задачи, а целого класса задач этого типа; 1) понятность; 2) детерминированность; 3) дискретность; 4) массовость.
Что называют служебными словами в алгоритмическом языке:
слова, употребляемые для записи команд, входящих в СКИ;
слова, смысл и способ употребления которых задан раз и навсегда;
вспомогательные алгоритмы, которые используются в составе других алгоритмов;
константы с постоянным значением?
Рекурсия в алгоритме будет прямой, когда:
рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.
Рекурсия в алгоритме будет косвенной, когда:
рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.
Команда машины Поста имеет структуру п Km, где:
n — порядковый номер команды; К— действие, выполняемое головкой; m — номер клетки, с которой данную команду надо произвести.
Сколько существует команд у машины Поста: 1) 2; 2) 4; 3) 6; 4) 8?
В машине Поста останов будет результативным:
при выполнении недопустимой команды;
если машина не останавливается никогда;
если результат выполнения программы такой, какой и ожидался;
В машине Поста некорректным алгоритм будет в следующем случае:
при выполнении недопустимой команды;
результат выполнения программы такой, какой и ожидался;
машина не останавливается никогда;
В машине Тьюринга рабочий алфавит:
В машине Тьюринга состояниями являются:
В машине Тьюринга предписание L для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево; 3) остановить машину;
4) занести в ячейку символ.
В машине Тьюринга предписание R для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево; 3) остановить машину;
4) занести в ячейку символ.
В машине Тьюринга предписание S для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
В алгоритме Маркова ассоциативным исчислением называется:
совокупность всех слов в данном алфавите;
совокупность всех допустимых систем подстановок;
совокупность всех слов в данном алфавите вместе с допустимой системой подстановок;
когда все слова в алфавите являются смежными.
В ассоциативном счислении два слова называются смежными:
если одно из них может быть преобразовано в другое применением подстановок;
если одно из них может быть преобразовано в другое однократным применением допустимой подстановки;
когда существует цепочка от одного слова к другому и обратно;
когда они дедуктивны.
ассоциативной; 2) эквивалентной; 3) индуктивной; 4) дедуктивной.
ассоциативными; 2) эквивалентными; 3) индуктивными; 4) дедуктивными.
В алгоритмах Маркова дана система подстановок в алфавите А = <а, b, с>:
abc — с; ba — cb; са — аb.
Преобразуйте с помощью этой системы слово bacaabc:
1) cbc; 2) ccbcbbc; 3) cbacba; 4) cbabc.
В алгоритмах Маркова дана система подстановок в алфавите А = <а, b, с>:
cb — abс; bac — ac; саb — b.
Преобразуйте с помощью этой системы слово bcabacab:
1) ccb; 2) cab; 3) cbc; 4) bcaab.
Способ композиции нормальных алгоритмов будет суперпозицией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;
алгоритм D будет суперпозицией трех алгоритмов А В С, причем область определения D является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения D(p)=A(p), если С(р) = е, D(p) = В(р), если С(р) = е, где е — пустая строка;
существует алгоритм С, являющийся суперпозицией алгоритмов А и B такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
Способ композиции нормальных алгоритмов будет объединением, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;
алгоритм D будет суперпозицией трех алгоритмов А В С, причем область определения D является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения D(p) = A(p), если С(р) = е, D(p) = В(р), если С(р) = е, где е — пустая строка;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
Способ композиции нормальных алгоритмов будет разветвлением, если:
1) выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;
алгоритм D будет суперпозицией трех алгоритмов A B C, причем область определения D является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения D(p) = А(р), если С(р) = е, D(p) — В(р), если С(р) = е, где е — пустая строка;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
Способ композиции нормальных алгоритмов будет итерацией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;
алгоритм D будет суперпозицией трех алгоритмов A B C, причем область определения D является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения
D(p) = А(р), если С(р) = е, D(p) — В(р), если С(р) = е, где е — пустая строка;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
Выбери правильный ответ
Команда машины Поста имеет структуру nKm, где:
Выбери правильный ответ
Сколько существует команд у машины Поста?
Выбери правильный ответ
В машине Поста останов будет результативным:
При выполнении недопустимой команды
Если машина не останавливается никогда
Если результат выполнения программы такой, какой и ожидался
Выбери правильный ответ
В машине Поста некорректным алгоритм будет в следующем случае:
При выполнении недопустимой команды
Результат выполнения программы такой, какой и ожидался
Машина не останавливается никогда
Выбери правильный ответ
В машине Тьюринга предписание L для лентопротяжного механизма означает:
Переместить ленту вправо
Переместить ленту влево
Занести в ячейку символ
Выбери правильный ответ
В машине Тьюринга предписание R для лентопротяжного механизма означает:
Переместить ленту вправо
Переместить ленту влево
Занести в ячейку символ
Выбери правильный ответ
В машине Тьюринга предписание S для лентопротяжного механизма означает:
Переместить ленту вправо
Переместить ленту влево
Занести в ячейку символ
Выбери правильный ответ
В алгоритме Маркова ассоциативным исчислением называется:
Совокупность всех слов в данном алфавите
Совокупность всех допустимых подстановок
Совокупность всех слов в данном алфавите вместе с допустимой системой подстановок
Когда все слова в алфавите являются смежными
Выбери правильный ответ
В ассоциативном исчислении два слова называются смежными:
Если одно из них может быть преобразовано в другое применением подстановок
Когда существует цепочка от одного слова к другому и обратно
Когда они дедуктивны
Если одно из них может быть преобразовано в другое однократным применением допустимой подстановки
Выбери правильный ответ
В алгоритме Маркова дана цепочка Р Р1, Р2. Рn. Если слова Р1, Р2. Рn смежные, то цепочка называется:
Выбери правильный ответ
В алгоритме Меркова дана цепочка Р Р1, Р2. Рк. Если слова Р1, Р2. Рк смежные и цепочка существует и в обратную сторону, то слова Р1 и Рк называют:
Выбери правильный ответ
Выбери правильный ответ
Вобери правильный ответ
Способ композиции нормальных алгоритмов будет суперпозицией, если:
Существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В
Выходное слово первого алгоритма является входным для второго
Существует алгоритм С, являющийся суперпозицией алгоритмов А и Д такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В
Выбери правильный ответ
Способ композиции нормальных алгоритмов будет объединением, если:
Входное слово первого алгоритма является входным для второго
Существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В
Существует алгоритм С, являющийся суперпозицией алгоритмов А и Д такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В
Выбери правильный ответ
Способ композиции нормальных алгоритмов будет разветвлением, если:
Выходное слово первого алгоритма является входным для второго
Существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В
Существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В
Выбери правильный ответ
Способ композиции нормальных алгоритмов будет итерацией, если:
Выходное слово первого алгоритма является входным для второго
Существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В
Существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В
83. В машине Тьюринга предписание L для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
84. В машине Тьюринга предписание R для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
85. В машине Тьюринга предписание S для лентопротяжного механизма означает:
1) переместить ленту вправо; 2) переместить ленту влево;
3) остановить машину; 4) занести в ячейку символ.
86. В алгоритме Маркова ассоциативным исчислением называется:
совокупность всех слов в данном алфавите;
совокупность всех допустимых систем подстановок;
совокупность всех слов в данном алфавите вместе с допустимой системой
подстановок;
когда все слова в алфавите являются смежными.
87. В ассоциативном счислении два слова называются смежными:
если одно из них может быть преобразовано в другое применением подстановок;
если одно из них может быть преобразовано в другое однократным применением допустимой подстановки;
когда существует цепочка от одного слова к другому и обратно;
когда они дедуктивны.
смежные, то цепочка называется:
90. В алгоритмах Маркова дана система подстановок в алфавите Л = <а, Ь, с>:
abc — с
91. В алгоритмах Маркова дана система подстановок в алфавите А = <а, Ь, с>:
cb — abc
92. Способ композиции нормальных алгоритмов будет суперпозицией, если:
1)выходное слово первого алгоритма является входным для второго;
2)существует алгоритм С, преобразующий любое слово р, содержащееся пересечении областей определения алгоритмов А и В;
4)существует алгоритм С, являющийся суперпозицией алгоритмов А и Д такой, что для любого входного слова р С<р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
93 Способ композиции нормальных алгоритмов будет объединением, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
существует алгоритм С, являющийся суперпозицией алгоритмов А и Д
такой, что для любого входного слова р С(р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
94. Способ композиции нормальных алгоритмов будет разветвлением, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
существует алгоритм С, являющийся суперпозицией алгоритмов А и В,
такой, что для любого входного слова р С<р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В.
95. Способ композиции нормальных алгоритмов будет итерацией, если:
выходное слово первого алгоритма является входным для второго;
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В;
4) существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
96. Свойство алгоритма записываться в виде упорядоченной совокупности отделенных друг от друга предписаний (директив):
1) понятность; 2) определенность; 3) дискретность; 4) массовость.
97. Свойство алгоритма записываться в виде только тех команд, которые находятся в Системе Команд Исполнителя, называется:
1) понятность; 2) определенность; 3) дискретность; 4) результативность.
98. Свойство алгоритма записываться только директивами однозначно и одинаково интерпретируемыми разными исполнителями:
1) понятность; 2) определенность; 3) дискретность; 4) результативность.
99.Свойство алгоритма, что при точном исполнении всех предписаний процесс
должен прекратиться за конечное число шагов с определенным ответом на поставленную задачу:
1) понятность; 2) детерминированность; 3) дискретность; 4) результативность.
100. Свойство алгоритма обеспечения решения не одной задачи, а целого класса
задач этого типа:
1) понятность; 2) определенность; 3) дискретность; 4) массовость.