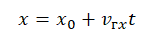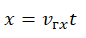В некий момент времени координата автомобиля

§ 1.7. Средняя скорость при неравномерном прямолинейном движении. Мгновенная скорость

Ни одно тело не движется все время с постоянной скоростью. Трогаясь с места, автомобиль начинает двигаться все быстрее и быстрее. Некоторое время он может двигаться равномерно, но рано или поздно замедляет движение и останавливается. При этом он проходит различные расстояния за одни и те же интервалы времени.

Что же надо понимать под скоростью, если тело движется неравномерно?

Средняя скорость

Введем понятие средней скорости неравномерного движения за интервал времени At.

Средней (по времени) скоростью неравномерного движения точки называется отношение изменения ее координаты Δх к интервалу времени Δt, в течение которого это изменение произошло:

Средняя скорость характеризует движение в течение интервала времени Δt именно в среднем и ничего не говорит о том, как же движется автомобиль в различные моменты времени этого интервала.

Другой пример. На рисунке 1.14 показан график скорости спринтера при забеге на 200 м. Проанализируем этот забег. Будем считать беговую дорожку прямолинейной. С точки зрения результата нас, конечно, интересует время забега (Δt = 20 с), и поэтому бег спортсмена можно характеризовать средней скоростью. Если координатную ось X совместить с беговой дорожкой (за начало отсчета можно принять точку на линии старта), то Δx = 200 м. Тогда v_x = = 10 м/с.

Но спортсмена и его тренера интересуют и детали забега: сколько времени длился разбег, какую скорость развил спортсмен в конце разбега (точка В на графике). Ведь этим и будет определяться время забега. Но скорость спортсмена, соответствующая точке В графика, это уже не средняя скорость, а скорость спортсмена в момент времени t = 4 с.

Мгновенная скорость

Мгновенную скорость естественно было бы определить как скорость тела в данный момент времени или в данной точке траектории. На первый взгляд определение очень простое и понятное. Но так ли это? Как надо, например, понимать следующее утверждение: «Скорость автомобиля в момент начала торможения была 90 км/ч»? Перефразировка этого утверждения «В момент начала торможения автомобиль за 1 ч прошел 90 км » бессмысленна.

Утверждение это, видимо, понимать надо так: если бы начиная с указанного момента времени автомобиль не стал бы тормозить, а продолжал бы двигаться так же, т. е. с той же быстротой, то за 1 ч он прошел бы 90 км, за 0,5 ч — 45 км, за 1 мин — 1,5 км, за 1 с — 25 м и т. д.

Результат последнего рассуждения весьма важен, ибо показывает, как в принципе можно определить мгновенную скорость автомобиля в момент t начала торможения (или любого другого тела, движущегося прямолинейно и неравномерно). Надо измерить среднюю скорость автомобиля на интервале времени от t до t + Δt и согласиться, что мгновенная скорость автомобиля в момент времени t приблизительно равна этой средней скорости. Приближение будет тем лучше и, следовательно, мгновенная скорость будет определена тем точнее, чем меньше промежуток времени Δt. Ведь надо, чтобы на этом промежутке скорость менялась незначительно, а лучше, чтобы этим изменением вообще можно было пренебречь. Последнее замечание заставляет нас брать величину Δt все меньше и меньше, не ставя ограничения этому уменьшению. В математике это называют «стремление интервала времени Δt к нулю» и обозначают «Δt —> 0».

За очень малый промежуток времени от t до t + Δt координата тела изменится также на малую величину Δх. Чтобы найти мгновенную скорость в момент времени t, надо малую величину Δх разделить на малую величину Δt и посмотреть, чему будет равно частное, если промежуток Δt неограниченно уменьшать, т. е. стремить к нулю. В математике говорят: «Найти предел отношения при стремлении Δt к нулю» и записывают: , где знак lim означает «предел».

Поясним сказанное на примере, когда движение тела описывается аналитически (формулой). Ведь по формуле можно найти положение тела в любой момент времени.

Пусть при движении тела вдоль оси X его координата изменяется согласно уравнению

Найдем теперь отношения изменений координаты к тем промежуткам времени, за которые эти изменения произошли:

Результаты вычислений приведены в таблице 2.

Таблица 2

Из таблицы видно, что по мере приближения интервала времени Δt к нулю отношение приближается к определенному значению (пределу), равному 10 м/с; это и есть скорость в момент времени t1 = 1 с.

Тогда для отношения получим:

= 2kt + kΔt.

Предел этого отношения при Δt —> 0 (мгновенная скорость) равен

Для данных нашего примера v_x = 10 м/с.

Таким образом, для любого момента времени отношение изменения координаты тела к промежутку времени, за который это изменение произошло, стремится к определенному значению при стремлении самого промежутка времени к нулю. Полученный вывод справедлив для любого неравномерного движения.

По определению имеем:

В математике выражение принято обозначать .

Тогда формулу (1.7.1) можно записать так:

Выражение называется производной координаты по времени.

Иногда производную обозначают иначе: (читается «икс-штрих»).

Когда мы говорим, что скорость в данный момент времени равна 10 м/с, то это означает следующее: если бы начиная с этого момента тело продолжало двигаться равномерно целую секунду, то оно прошло бы 10 м. При равномерном движении средняя скорость за любой момент времени равна мгновенной. В дальнейшем вы убедитесь, что именно мгновенная, а не средняя скорость играет в механике основную роль.

Как измерить мгновенную скорость

Измерить мгновенную скорость, осуществив экспериментально предельныи переход при Δt —» О, практически невозможно. Используя стробоскопические фотографии (рис. 1.15), можно измерить координаты тела в очень близкие моменты времени и вычислить средние скорости между этими моментами. Но мгновенную скорость так определить нельзя.

Для измерения (разумеется, приближенного) используют различные явления, которые зависят от мгновенной скорости. Так, в спидометре автомобиля гибкий тросик передает вращение от ведомого вала коробки передач к маленькому постоянному магниту. Вращение магнита возбуждает электрический ток в катушке, в результате чего происходит поворот стрелки спидометра.

Чтобы узнать скорость самолета, измеряют давление встречного потока воздуха. В радарах используют изменение частоты радиоволн при отражении от движущихся тел.

При неравномерном движении скорость изменяется. Некоторое представление о движении дает средняя скорость. Но главную роль играет скорость в любой точке в данный момент времени. Это — мгновенная скорость.

Рисунок с фотографии двух падающих шариков различной массы. Фотографию получили, открывая объектив и чередуя вспышки света каждые 1/30 с. Заметьте, что маленький шарик достигает пола одновременно с большим. Оба шарика начинают падать одновременно.

1 Здесь и в дальнейшем черта над обозначением величины означает среднее значение этой величины.

2 Потом мы увидим, что именно так меняется координата падающего на землю с небольшой высоты камня.

3 Строго говоря, здесь речь идет об определении проекции мгновенной скорости на ось X (см. § 1.12).

Источник

Равномерное прямолинейное движение

4. Зависимость координаты тела от времени можно представить графически.

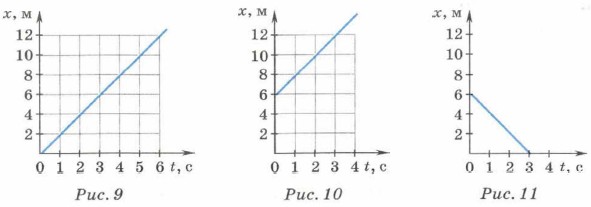
Предположим, что тело движется из начала координат в направлении оси X с постоянной скоростью. Проекция скорости тела на эту ось равна 2 м/с. Уравнение движения в этом случае имеет вид: х = 2t (м). Зависимость координаты тела от времени — линейная. Графиком такой зависимости является прямая, проходящая через начало координат (рис. 9).

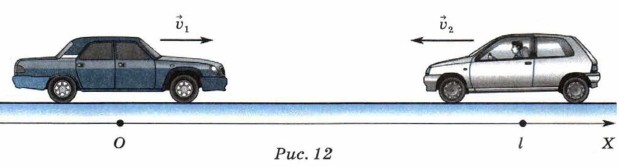
Если в начальный момент времени координата тела х₀ = 6 м, а проекция его скорости υ_x = 2 м/с, то уравнение движения имеет вид: х = 6 + 2t (м). Это тоже линейная зависимость координаты тела от времени, и её графиком является прямая, проходящая через точку, для которой при t = 0 x = 6m (рис. 10).

Таким образом, движение тела может быть описано аналитически, т. е. с помощью уравнения движения, и графически, т. е. с помощью графика зависимости координаты тела от времени.

5. Пример решения задачи

При решении задач необходимо выполнять следующую последовательность действий.

1. Кратко записать условие задачи.

2. Проанализировать ситуацию, описанную в условии задачи:

— выяснить, можно ли принять движущиеся тела за материальные точки;

— сделать рисунок, изобразив на нём векторы скорости;

— выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.

3. Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости на координатные оси.

4. Решить задачу в общем виде.

5. Подставить в формулу значения величин и выполнить вычисления.

6. Проанализировать ответ.

Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один — со скоростью 10 м/с, другой — со скоростью 20 м/с. Определите время и координату места встречи автомобилей, если в начальный момент времени расстояние между ними равно 120 м.

1-й способ. Свяжем систему отсчёта с Землёй, ось ОХ направим в сторону движения первого автомобиля, за начало отсчёта координаты выберем точку О — положение первого автомобиля в начальный момент времени (рис. 12).

В начальный момент времени координаты каждого тела равны: х₀₁ = 0; х₀₂ = l.

Запишем уравнение движения: х = х₀ + vυ_xt.

Уравнения движения для каждого тела с учётом начальных условий имеют вид:

В момент встречи тел х₁ = х₂, следовательно:

Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей:

х = 10 м/с • 4 с = 40 м.

Источник

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t₁ = 0 с, а t₂ = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает вид:

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два корня: t₁ = 0,6 с, а t₂ = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение. Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет вид:

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Теперь мы можем выделить кинематические характеристики движения тела:

Перемещение тела определяется формулой:

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

Кинетическая энергия тела определяется формулой:

Скорость при прямолинейном равноускоренном движении равна:

v = v 0 + a t = 5 − 6 t

Поэтому кинетическая энергия тела равна:

Следовательно, правильная последовательность цифр в ответе будет: 34.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник