взаимно обратные арифметические действия в практике вычислений применяются для
Открытый урок по математике «Взаимно-обратные действия: умножение и деление», 3-й класс
Класс: 3
1. Организационный момент.
-Ребята, у нас сегодня важный урок. Создадим хорошее, дружелюбное настроение. Улыбнитесь друг другу, гостям, садитесь. Как будем работать на уроке? Слажено, дружно.
-Руки? – На месте.
-Ноги? – На месте.
— Локти? – У края.
-Спина? – Прямая!
2. Проверка домашнего задания (взаимопроверка).
Откройте тетради, запишите число, классная работа. Прочитайте это число. (23=)
Сколько цифр использовано для записи. Как называются такие числа? Запишите его в виде суммы разрядных слагаемых. 1 в. – составьте и запишите двузначное число, используя только цифру 2, 2 в. – используя только цифру 3. Минутка чистописания
(Ответы записываются детьми в паре на листочках.)
Игра “Заполни окошки”.
Задание на внимание. На уроках необходимо быть очень внимательными. Потренируемся в этом. Постройте глазами прямоугольник, квадрат, проведите глазами по периметру доски, “напишите” головой слово умножение, деление.
-Ребята, сосчитайте, сколько треугольников на рисунке?
—Оцените свою работу в ходе устного счета:
Л. – легко
И. – интересно
Т. – трудно4. Объявление темы урока.
— Ребята, я предлагаю вам сегодня на уроке представить себя в роли будущих учёных и исследовать ещё одну очень важную тему. Согласны? А, когда ученые исследуют что-то, они обязательно проверяют все, что связано с предметом изучения. Значит, сначала необходимо узнать название темы. Хотите узнать?
С учеными могут происходить самые удивительные и непредвиденные ситуации при достижении целей своих исследований. Чтобы добиться целей и выйти достойно из таких ситуаций, потребуется ваше внимание, логика, знания, желание, а, значит, будут необходимы ваша дружба, слаженность в работе, организованность.
— Какие же цели поставим, исходя из темы:
1. что будем исследовать…
2. что нового узнаем…
Верно, ваши цели совпали с моими.
5. Работа над темой.
— Таким образом, мы выполним задания по данной теме и проведем математическое исследование, цель которого, узнать, какие еще взаимно-обратные действия есть в математике.
— Вспомните, с какими взаимно-обратными действиями вы познакомились на прошлом уроке? Стр. 74-75 учебника № 1 рассмотрите устно. Чем похожи эти примеры?
Как называются числа при умножении? Что является неизвестным в этих примерах?
Что нужно сделать, чтобы найти неизвестный множитель? Какое действие выполним?
Дети делают вывод: обратное действие умножению – это деление и наоборот.
6. Первичное закрепление.
— Ребята, рассмотрите № 2 и № 3 (с.74)
— Какие фигуры изображены?
— Назовите одним словом. (Прямоугольники)
— Докажите, что это прямоугольники.
— Что нужно вычислить? (Площади прямоугольников)
— Все ли известно для этого? (Да)
— С помощью какого действия найдете их площади?
— Вспомните правило нахождения площади, формулу.
— Запишите решение и ответ по рядам: 1 ряд – синего прямоугольника, 2 – оранжевого прямоугольника, 3- желтого прямоугольника.
— Ребята, проверим правильность выполнения этого задания.
— А теперь исследуем фигуры из № 3.
— Что известно у следующих геометрических фигур? Что нужно найти? Как же узнать длину второй стороны фигуры, если известна ее площадь и длина одной стороны? Сформулируйте правило. Какое действие выполним, чтобы найти длину второй стороны?
-Я считаю, что ученые могут быстро и правильно решать задачи разной сложности.
Следует ли нам брать с них пример и также справляться с решением задач?
Таким образом, я предполагаю, что мы достойно справимся с решением задачи № 5 стр. 74 учебника и проверим мое предположение.
-Прочитайте внимательно шепотом условие задачи.
Ученик еще раз читает условие задачи с выделением данных.
-О ком говорится в задаче?
-Что показывает число 8?
-Что еще известно в задаче?
-Что надо узнать? Прочитайте главный вопрос задачи.
-Можно ли сразу ответить на главный вопрос задачи? Какая особенность у задачи?
-Что мы сначала будем узнавать?
-А потом сможете найти ответ задачи?
— Ребята, рассмотрите краткую запись и дополните её.
— Повторите условие задачи по краткой записи. Замечательно.
— Решайте задачу самостоятельно.
(За доской задачу решает ученик.)
— Ребята, проверим правильность решения задачи:
-Как вы узнали, сколько щупалец у медузы?
-Как узнали, у кого их меньше и во сколько раз?
-Прочитайте ответ задачи. У остальных получилось также? Молодцы!
-Значит мое предположение о том, что вы умеете решать разные задачи, подтвердилось.
-Оцените свою работу в ходе решения задачи.
-После проделанной работы всем необходим отдых. Великие ученые тоже нуждаются в отдыхе. Вы много работали, пришла пора отдохнуть.
-Ребята, как вы думаете, ученые берегут время или могут позволить себе, например, просто “убивать время”? Как вы понимаете значение фразеологизма “убивать время”?
-А 1 минута – это много или мало? Дело в том, что каждую минуту в нашей стране производят 13 телевизоров. 11 холодильников, 1560 пар обуви, 77 часов, 3 автомашины – подсчитали ученые. Вот и мы за оставшееся время постараемся сделать как можно больше заданий.
2. 3-е ребят работают у доски по карточкам.
3. Cамостоятельная работа – дифференцированные задания (для остальных учащихся)
-Найдите №8 стр. 75. Сейчас вы будете решать примеры по уровням сложности. Примеры под буквой а) – это 1 уровень, легкий, а примеры под буквами б) и в) – это примеры 2-го уровня, более сложного. Определитесь с примерами, которые, как вы считаете, соответствуют вашим возможностям. Поднимите руки, кто выбрал 1-ый уровень, а теперь те, кто выбрал 2-ой уровень. Отлично, решайте в тетрадях.
— Ребята, проверим выполненное вами задание.
Каждая группа получает карточку с заданием. Выбирает капитана. Начинает работу.
— Ребята, проверим выполненное вами задание и определим,
какая группа справилась правильно и быстро.
Работать вам, ребята, необходимо в паре.
Последовательность описанных в задаче действий дети изображают в виде цепочки:
(Ребята делают вывод: число очков увеличилось)
8. Подведение итогов.
-С какой темой познакомились?
-Какие взаимно-обратные действия знаете?
-Где вам понадобятся знания о таких действиях?
-Оцените урок: было легко, интересно, трудно.
-Вывод: в роли ученых интересно быть, т.к., они умеют многое, а вы будете дальше учиться, чтобы узнавать много нового и интересного.
9. Домашнее задание (инструктаж).
Конспект урока математике по теме: «Взаимно обратные арифметические действия».
В документе содержится конспект по теме: «Взаимообратные арифметические действия».
Просмотр содержимого документа
«Конспект урока математике по теме: «Взаимно обратные арифметические действия».»Урок по математике во 2 классе. Тема: «Взаимно обратные арифметические действия».
Урок 2 Повторение. Закрепление.
*Получить достоверные данные об уровне представлений учащихся по данной теме, о сформированности их знаний и умений.
*Повторить и закрепить знания, умения, приобретённые на предыдущих занятиях:
1. Знаковую запись римских чисел.
2. Конкретный смысл действия умножения.
3. Признаки отличий квадрата равностороннего треугольника.
*Учиться воспринимать сложение и вычитание умножение и деление как взаимно обратные действия.
*Учиться работать в команде (в группе):
— соблюдать правила общения со сверстниками;
— соблюдать правила поведения в школе.
Виды заданий выбраны грамотно и соответствуют теме и целям занятия, которые направлены на развитие личностных, познавательных, коммуникативных УУД.
Присутствуют различные виды активности: познавательная, социальная и физическая. Применяются здоровье сберегающие технологии (физкультминутка, динамическая пауза).
Применены интерактивные формы организации занятия.
Применён принцип оценивания – похвалы подбадривания и поддержки.
Ведущую роль занимают учащиеся, как главные участники урока.
Учитель направляет и поддерживает работу учащихся.
Предметно – развивающая и информационная среда достаточно хорошо подготовлены. На уроке просматривалась связь «ученик – ученик – учитель – ученик»
Подведение итогов с самооценкой знаний.
Универсальные учебные действия
Личностные универсальные учебные действия
Регулятивные универсальные учебные действия
Познавательные универсальные учебные действия
— Звонко прозвенел звонок!
Все явились на урок?
Дружно рядом с партой встали
И готовность показали!
Все учебники, тетрадки
В уголке лежат в порядке
И в пенале ручка есть?
Разрешаю вам присесть!
У обучающегося будут сформированы:
– внутренняя позиция школьника на уровне
положительного отношения к урокам математики;
– понимание роли математических действий
– интерес к различным видам учебной деятельности, включая элементы предметно исследовательской деятельности;
– ориентация на понимание предложений
и оценок учителей и одноклассников;
– понимание нравственного содержания поступков окружающих людей.
Обучающийся получит возможность для
– интереса к познанию математических
фактов, математических зависимостей
– первоначальной ориентации на оценку результатов познавательной деятельности;
– общих представлений о рациональной организации мыслительной деятельности;
– самооценки на основе заданных критериев успешности учебной деятельности;
– первоначальной ориентации в поведении
на принятые моральные нормы;
– понимания чувств одноклассников, учите
– принимать учебную задачу и следовать
– планировать свои действия в соответствии
с учебными задачами;
— Как обычно, устный счёт нас в разминке этой ждёт!
Выполнив задание, вы узнаете, который час соответствует
понятию «полдень»:Замените арабские последние три числа в закономерности римскими.
3.Повторение ранее изученного. Закрепление и индивидуальная работа, а также работа в группах.
— Всем спасибо, молодцы! Продолжаем работу. Анализ домашнего задания по итогам проверки предыдущей работы учителем.
— Некоторые ребята допустили серьёзную ошибку в решении задачи в домашнем задании. Мы рассмотрим Подобную задачу. ( Повторение конкретного смысла умножения)
(задача из дополнительного учебника). Чтение задачи самостоятельно.
— Ребята, кто видел, как растёт горох на грядках? (Рассказ о растении.)
Самостоятельное решение задачи в тетрадях и 2 ученика на доске. С последующей проверкой.
В двух стручках по 6 горошин. Сколько горошин в этих стручках?
У доски решает ученик, допустивший ошибку в домашнем задании и ученик, решивший правильно задачу. Остальным ученикам предлагается решать задачу с помощью рисунка, схемы или палочек.
— Решили? Спасибо садитесь на место.
На доске, как и ожидалось, две разных записи решения задачи:
2х6=12 (гор.) 2) 6х2=12(гор.)
Далее идёт анализ решения задачи учениками.
(У)- Саша не прав, потому что он на первом месте записал количество стручков, а надо писать количество горошин.
— Это имеет какое- то значение?
(У) – Да имеет. В задаче спрашивается о горошинах, значит, если задачу решать действием сложения, то мы будем складывать по 6 горошин 2 раза, т. к. у нас дано 2 стручка.
Далее рассматриваются графические способы записи задачи:
Изображение, закодированное геометрическими фигурами во множествах.
6 + 6 = 6 х 2 = 12 (гор.)
Ответ: 12 горошин в 2-х стручках.
— Какие правила надо помнить, чтобы решать задачи такого типа?
Надо внимательно прочитать и проанализировать условие задачи и вопрос.
Найти данные задачи и соотнести их с вопросом.
Постараться понять смысл задачи соотнести его с понятием конкретного действия умножения, т. е. вспомнить какое число из данных стоит в произведении на 1-ом месте,
Если возникли трудности, нарисовать рисунок или схему, или поработать с палочками.
Записать решение и ответ.
– учитывать выделенные учителем ориентиры действия в учебном материале;
– в сотрудничестве с учителем находить не
сколько вариантов решения учебной задачи,
представленной на наглядно образном уровне;
– вносить необходимые коррективы в действия на основе принятых правил;
– выполнять учебные действия в устной
– принимать установленные правила в
планировании и контроле способа решения;
– осуществлять пошаговый контроль под руководством учителя в доступных видах учеб
но познавательной деятельности.
Обучающийся получит возможность научиться:
– понимать смысл инструкции учителя и заданий, предложенных в учебнике;
– выполнять действия в опоре на заданный
– воспринимать мнения и предложения сверстников о способе решения задачи;
– на основе вариантов решения практических задач под руководством учителя делать выводы о свойствах изучаемых объектов;
– выполнять учебные действия в устной,
письменной речи и во внутреннем плане;
– самостоятельно оценивать правильность
выполнения заданий и вносить необходимые
коррективы в действия с наглядно образным материалом.
– осуществлять поиск нужной информации,
используя материал учебника и справочную
– использовать рисуночные и символические
варианты математической записи;
– на основе кодирования строить несложные
модели математических понятий, задачных
– кодировать информацию в знаково символической форме;
– строить небольшие математические сообщения в устной форме (до 4–5 предложений);
– проводить сравнение, понимать выводы,
сделанные на основе сравнения;
– выделять в явлениях существенные и не
существенные, необходимые и достаточные
– проводить аналогию и на ее основе строить выводы;
– в сотрудничестве с учителем проводить
классификацию изучаемых объектов;
Подведение к теме занятия.
1.
— Что общего в данных равенствах первой строки?
(У) – Применяются одинаковые числа.
(У) – Разные знаки арифметических действий.
— Какие действия применяются?
— Что можем ещё сказать о данных математических действиях?
Действие вычитание является обратным сложению.
Что общего в данных равенствах второй строки?
(У) – Применяются одинаковые числа.
(У) – Разные знаки арифметических действий.
— Какие действия применяются?
— Что можем ещё сказать о данных математических действиях?
(У) – Действие деление – это обратное действие умножению.
— Найдите значение выражения.
— Как искали значение произведения
-Заменяли умножение сложением.
— Запишите к данному равенству обратное действие.
7 х 8 = 56 ( 56 : 7 = 8 56 : 8 =7 )
— Как находили значение частного?
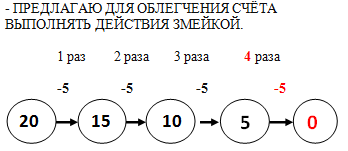
— А как вы думаете, если действие умножение одинаковых слагаемых можно заменить умножением, то можно ли найти сколько раз число 5 помещается в числе 20 действием вычитания?
(У) – Я думаю, что можно. Нужно из числа 20 вычитать несколько раз число 5.
-Давайте проверим наше предположение.
(Ученик идёт к доске)
-Посчитайте сколько раз число 5 уместилось в числе 20?
— Предлагаю для облегчения счёта выполнять действия змейкой.
У обучающегося будут сформированы:
– внутренняя позиция школьника на уровне
положительного отношения к урокам математики;
– понимание роли математических действий
– интерес к различным видам учебной деятельности, включая элементы предметно исследовательской деятельности;
– ориентация на понимание предложений
и оценок учителей и одноклассников;
– понимание нравственного содержания поступков окружающих людей.
Обучающийся получит возможность для
– интереса к познанию математических
фактов, математических зависимостей
– первоначальной ориентации на оценку результатов познавательной деятельности;
– общих представлений о рациональной организации мыслительной деятельности;
– самооценки на основе заданных критериев успешности учебной деятельности;
– первоначальной ориентации в поведении
на принятые моральные нормы;
– понимания чувств одноклассников, учителей.
Обучающийся получит возможность научиться:
– самостоятельно оценивать правильность
выполнения заданий и вносить необходимые
коррективы в действия с наглядно образным материалом.
простые индуктивные и дедуктивные рассуждения.
Обучающийся получит возможность на
– под руководством учителя осуществлять
поиск необходимой и дополнительной информации;
– работать с дополнительными текстами
– соотносить содержание схематических
изображений с математической записью;
– моделировать задачи на основе анализа
Контроль, самопроверка и взаимопроверка знаний.
Повторение изученного с применением нового знания.
Найдите значения частных в выражениях с помощью нашей змейки.
(Данный способ развивает не только умение осмысленно находить сколько раз помещается в делимом число делителя, но и развивает вычислительный навык при нахождении каждого промежуточного действия, часто с переходом через разрядную единицу.)
— Поменяйтесь тетрадями, помогите друг другу, если нашли ошибку.
— Продолжаем нашу работу.
— Прочитайте задание. Какие знания и умения вам понадобятся?
Измерьте длинный кусок проволоки (длина 12 см, приготовлено заранее). Найдите длину стороны квадрата, полученного из проволоки равной длине вашего отрезка.
(У) – Надо знать, как находить периметр квадрата.
— Верно! Молодец! Покажи на доске твоё решение.
(У)- Получилось, что 4 раза взяли по 3 см. Длина стороны квадрата равна 3см.
— Поработайте в парах со вторым куском проволоки. Сложите из него равносторонний треугольник. Найдите длину его стороны.
У обучающегося будут сформированы:
– интерес к различным видам учебной деятельности, включая элементы предметно исследовательской деятельности;
– ориентация на понимание предложений
и оценок учителей и одноклассников;
Обучающийся получит возможность для
– интереса к познанию математических
фактов, математических зависимостей
– общих представлений о рациональной организации мыслительной деятельности;
– устанавливать аналогии; формулировать
выводы на основе аналогии;
– строить рассуждения о математических
– пользоваться эвристическими приемами
для нахождения решения математических
— Что нового узнали сегодня на уроке?
1.Способ «Змейки», который помог нам понять смысл действия деления.
2.Применение этого способа в решении геометрической задачи.
— Чем ещё занимались на уроке?
3. Повторили и закрепили знание конкретного смысла действия умножения.
4. Повторили обратные математические действия.
5. Выполняли устный счёт.
6. Вспоминали римские числа.
— Что нужно уметь и знать, чтобы достичь целей?
1. Умения выполнять арифметические действия сложения, умножения, вычитания, деления.
2.Знать правило конкретного смысла умножения.
3.Знать определение квадрата и равностороннего треугольника.
Домашнее задание (номера из учебника).
Обучающийся получит возможность для
– самооценки на основе заданных критериев успешности учебной деятельности;
Конспект урока математике по теме: «Взаимно обратные арифметические действия».
В документе содержится конспект по теме: «Взаимообратные арифметические действия».
Просмотр содержимого документа
«Конспект урока математике по теме: «Взаимно обратные арифметические действия».»Урок по математике во 2 классе. Тема: «Взаимно обратные арифметические действия».
Урок 2 Повторение. Закрепление.
*Получить достоверные данные об уровне представлений учащихся по данной теме, о сформированности их знаний и умений.
*Повторить и закрепить знания, умения, приобретённые на предыдущих занятиях:
1. Знаковую запись римских чисел.
2. Конкретный смысл действия умножения.
3. Признаки отличий квадрата равностороннего треугольника.
*Учиться воспринимать сложение и вычитание умножение и деление как взаимно обратные действия.
*Учиться работать в команде (в группе):
— соблюдать правила общения со сверстниками;
— соблюдать правила поведения в школе.
Виды заданий выбраны грамотно и соответствуют теме и целям занятия, которые направлены на развитие личностных, познавательных, коммуникативных УУД.
Присутствуют различные виды активности: познавательная, социальная и физическая. Применяются здоровье сберегающие технологии (физкультминутка, динамическая пауза).
Применены интерактивные формы организации занятия.
Применён принцип оценивания – похвалы подбадривания и поддержки.
Ведущую роль занимают учащиеся, как главные участники урока.
Учитель направляет и поддерживает работу учащихся.
Предметно – развивающая и информационная среда достаточно хорошо подготовлены. На уроке просматривалась связь «ученик – ученик – учитель – ученик»
Подведение итогов с самооценкой знаний.
Универсальные учебные действия
Личностные универсальные учебные действия
Регулятивные универсальные учебные действия
Познавательные универсальные учебные действия
— Звонко прозвенел звонок!
Все явились на урок?
Дружно рядом с партой встали
И готовность показали!
Все учебники, тетрадки
В уголке лежат в порядке
И в пенале ручка есть?
Разрешаю вам присесть!
У обучающегося будут сформированы:
– внутренняя позиция школьника на уровне
положительного отношения к урокам математики;
– понимание роли математических действий
– интерес к различным видам учебной деятельности, включая элементы предметно исследовательской деятельности;
– ориентация на понимание предложений
и оценок учителей и одноклассников;
– понимание нравственного содержания поступков окружающих людей.
Обучающийся получит возможность для
– интереса к познанию математических
фактов, математических зависимостей
– первоначальной ориентации на оценку результатов познавательной деятельности;
– общих представлений о рациональной организации мыслительной деятельности;
– самооценки на основе заданных критериев успешности учебной деятельности;
– первоначальной ориентации в поведении
на принятые моральные нормы;
– понимания чувств одноклассников, учите
– принимать учебную задачу и следовать
– планировать свои действия в соответствии
с учебными задачами;
— Как обычно, устный счёт нас в разминке этой ждёт!
Выполнив задание, вы узнаете, который час соответствует
понятию «полдень»:Замените арабские последние три числа в закономерности римскими.
3.Повторение ранее изученного. Закрепление и индивидуальная работа, а также работа в группах.
— Всем спасибо, молодцы! Продолжаем работу. Анализ домашнего задания по итогам проверки предыдущей работы учителем.
— Некоторые ребята допустили серьёзную ошибку в решении задачи в домашнем задании. Мы рассмотрим Подобную задачу. ( Повторение конкретного смысла умножения)
(задача из дополнительного учебника). Чтение задачи самостоятельно.
— Ребята, кто видел, как растёт горох на грядках? (Рассказ о растении.)
Самостоятельное решение задачи в тетрадях и 2 ученика на доске. С последующей проверкой.
В двух стручках по 6 горошин. Сколько горошин в этих стручках?
У доски решает ученик, допустивший ошибку в домашнем задании и ученик, решивший правильно задачу. Остальным ученикам предлагается решать задачу с помощью рисунка, схемы или палочек.
— Решили? Спасибо садитесь на место.
На доске, как и ожидалось, две разных записи решения задачи:
2х6=12 (гор.) 2) 6х2=12(гор.)
Далее идёт анализ решения задачи учениками.
(У)- Саша не прав, потому что он на первом месте записал количество стручков, а надо писать количество горошин.
— Это имеет какое- то значение?
(У) – Да имеет. В задаче спрашивается о горошинах, значит, если задачу решать действием сложения, то мы будем складывать по 6 горошин 2 раза, т. к. у нас дано 2 стручка.
Далее рассматриваются графические способы записи задачи:
Изображение, закодированное геометрическими фигурами во множествах.
6 + 6 = 6 х 2 = 12 (гор.)
Ответ: 12 горошин в 2-х стручках.
— Какие правила надо помнить, чтобы решать задачи такого типа?
Надо внимательно прочитать и проанализировать условие задачи и вопрос.
Найти данные задачи и соотнести их с вопросом.
Постараться понять смысл задачи соотнести его с понятием конкретного действия умножения, т. е. вспомнить какое число из данных стоит в произведении на 1-ом месте,
Если возникли трудности, нарисовать рисунок или схему, или поработать с палочками.
Записать решение и ответ.
– учитывать выделенные учителем ориентиры действия в учебном материале;
– в сотрудничестве с учителем находить не
сколько вариантов решения учебной задачи,
представленной на наглядно образном уровне;
– вносить необходимые коррективы в действия на основе принятых правил;
– выполнять учебные действия в устной
– принимать установленные правила в
планировании и контроле способа решения;
– осуществлять пошаговый контроль под руководством учителя в доступных видах учеб
но познавательной деятельности.
Обучающийся получит возможность научиться:
– понимать смысл инструкции учителя и заданий, предложенных в учебнике;
– выполнять действия в опоре на заданный
– воспринимать мнения и предложения сверстников о способе решения задачи;
– на основе вариантов решения практических задач под руководством учителя делать выводы о свойствах изучаемых объектов;
– выполнять учебные действия в устной,
письменной речи и во внутреннем плане;
– самостоятельно оценивать правильность
выполнения заданий и вносить необходимые
коррективы в действия с наглядно образным материалом.
– осуществлять поиск нужной информации,
используя материал учебника и справочную
– использовать рисуночные и символические
варианты математической записи;
– на основе кодирования строить несложные
модели математических понятий, задачных
– кодировать информацию в знаково символической форме;
– строить небольшие математические сообщения в устной форме (до 4–5 предложений);
– проводить сравнение, понимать выводы,
сделанные на основе сравнения;
– выделять в явлениях существенные и не
существенные, необходимые и достаточные
– проводить аналогию и на ее основе строить выводы;
– в сотрудничестве с учителем проводить
классификацию изучаемых объектов;
Подведение к теме занятия.
1.
— Что общего в данных равенствах первой строки?
(У) – Применяются одинаковые числа.
(У) – Разные знаки арифметических действий.
— Какие действия применяются?
— Что можем ещё сказать о данных математических действиях?
Действие вычитание является обратным сложению.
Что общего в данных равенствах второй строки?
(У) – Применяются одинаковые числа.
(У) – Разные знаки арифметических действий.
— Какие действия применяются?
— Что можем ещё сказать о данных математических действиях?
(У) – Действие деление – это обратное действие умножению.
— Найдите значение выражения.
— Как искали значение произведения
-Заменяли умножение сложением.
— Запишите к данному равенству обратное действие.
7 х 8 = 56 ( 56 : 7 = 8 56 : 8 =7 )
— Как находили значение частного?
— А как вы думаете, если действие умножение одинаковых слагаемых можно заменить умножением, то можно ли найти сколько раз число 5 помещается в числе 20 действием вычитания?
(У) – Я думаю, что можно. Нужно из числа 20 вычитать несколько раз число 5.
-Давайте проверим наше предположение.
(Ученик идёт к доске)
-Посчитайте сколько раз число 5 уместилось в числе 20?
— Предлагаю для облегчения счёта выполнять действия змейкой.
У обучающегося будут сформированы:
– внутренняя позиция школьника на уровне
положительного отношения к урокам математики;
– понимание роли математических действий
– интерес к различным видам учебной деятельности, включая элементы предметно исследовательской деятельности;
– ориентация на понимание предложений
и оценок учителей и одноклассников;
– понимание нравственного содержания поступков окружающих людей.
Обучающийся получит возможность для
– интереса к познанию математических
фактов, математических зависимостей
– первоначальной ориентации на оценку результатов познавательной деятельности;
– общих представлений о рациональной организации мыслительной деятельности;
– самооценки на основе заданных критериев успешности учебной деятельности;
– первоначальной ориентации в поведении
на принятые моральные нормы;
– понимания чувств одноклассников, учителей.
Обучающийся получит возможность научиться:
– самостоятельно оценивать правильность
выполнения заданий и вносить необходимые
коррективы в действия с наглядно образным материалом.
простые индуктивные и дедуктивные рассуждения.
Обучающийся получит возможность на
– под руководством учителя осуществлять
поиск необходимой и дополнительной информации;
– работать с дополнительными текстами
– соотносить содержание схематических
изображений с математической записью;
– моделировать задачи на основе анализа
Контроль, самопроверка и взаимопроверка знаний.
Повторение изученного с применением нового знания.
Найдите значения частных в выражениях с помощью нашей змейки.
(Данный способ развивает не только умение осмысленно находить сколько раз помещается в делимом число делителя, но и развивает вычислительный навык при нахождении каждого промежуточного действия, часто с переходом через разрядную единицу.)
— Поменяйтесь тетрадями, помогите друг другу, если нашли ошибку.
— Продолжаем нашу работу.
— Прочитайте задание. Какие знания и умения вам понадобятся?
Измерьте длинный кусок проволоки (длина 12 см, приготовлено заранее). Найдите длину стороны квадрата, полученного из проволоки равной длине вашего отрезка.
(У) – Надо знать, как находить периметр квадрата.
— Верно! Молодец! Покажи на доске твоё решение.
(У)- Получилось, что 4 раза взяли по 3 см. Длина стороны квадрата равна 3см.
— Поработайте в парах со вторым куском проволоки. Сложите из него равносторонний треугольник. Найдите длину его стороны.
У обучающегося будут сформированы:
– интерес к различным видам учебной деятельности, включая элементы предметно исследовательской деятельности;
– ориентация на понимание предложений
и оценок учителей и одноклассников;
Обучающийся получит возможность для
– интереса к познанию математических
фактов, математических зависимостей
– общих представлений о рациональной организации мыслительной деятельности;
– устанавливать аналогии; формулировать
выводы на основе аналогии;
– строить рассуждения о математических
– пользоваться эвристическими приемами
для нахождения решения математических
— Что нового узнали сегодня на уроке?
1.Способ «Змейки», который помог нам понять смысл действия деления.
2.Применение этого способа в решении геометрической задачи.
— Чем ещё занимались на уроке?
3. Повторили и закрепили знание конкретного смысла действия умножения.
4. Повторили обратные математические действия.
5. Выполняли устный счёт.
6. Вспоминали римские числа.
— Что нужно уметь и знать, чтобы достичь целей?
1. Умения выполнять арифметические действия сложения, умножения, вычитания, деления.
2.Знать правило конкретного смысла умножения.
3.Знать определение квадрата и равностороннего треугольника.
Домашнее задание (номера из учебника).
Обучающийся получит возможность для
– самооценки на основе заданных критериев успешности учебной деятельности;