ансамблевый метод машинного обучения

Методы сбора ансамблей алгоритмов машинного обучения: стекинг, бэггинг, бустинг

Что такое ансамбли моделей?

Стекинг. Могут рассматриваться разнородные отдельно взятые модели. Существует мета-модель, которой на вход подаются базовые модели, а выходом является итоговый прогноз.

Бэггинг. Рассматриваются однородные модели, которые обучаются независимо и параллельно, а затем их результаты просто усредняются. Ярким представителем данного метода является случайный лес.

Бустинг. Рассматриваются однородные модели, которые обучаются последовательно, причем последующая модель должна исправлять ошибки предыдущей. Конечно, в качестве примера здесь сразу приходит на ум градиентный бустинг.

Рисунок 1

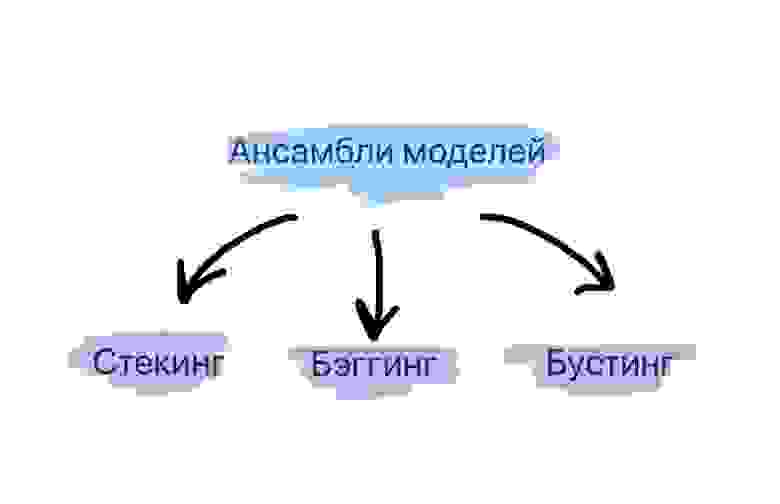
Три этих способа и будут детальнее рассмотрены далее.

Стекинг

Из трех вариантов стекинг является наименее популярным. Это можно проследить и по числу готовых реализаций данного метода в программных библиотеках. В том же sklearn.ensemble в python куда чаше используют AdaBoost, Bagging, GradientBoosting, чем тот же самый Stacking (хотя его реализация там тоже есть).

Стекинг выделяется двумя основными чертами: он может объединить в себе алгоритмы разной природы в качестве базовых. Например, взять метод опорных векторов (SVM), k-ближайших соседей (KNN) в качестве базовых и на основе их результатов обучить логистическую регрессию для классификации. Также стоит отметить непредсказуемость работы метамодели. Если в случае бэггинга и бустинга существует достаточно четкий и конкретный ансамблевый алгоритм (увидим далее), то здесь метамодель может с течением времени по-разному обучаться на входных данных.

Алгоритм обучения выглядит следующим образом (рис. 2):

Делим выборку на k фолдов (тот же смысл, что и в кросс-валидации).

Для объекта из выборки, который находится в k-ом фолде, делается предсказание слабыми алгоритмами, которые были обучены на k-1 фолдах. Этот процесс итеративен и происходит для каждого фолда.

Создается набор прогнозов слабых алгоритмов для каждого объекта выборки.

На сформированных низкоуровневыми алгоритмами прогнозах в итоге обучается метамодель.

Рисунок 2

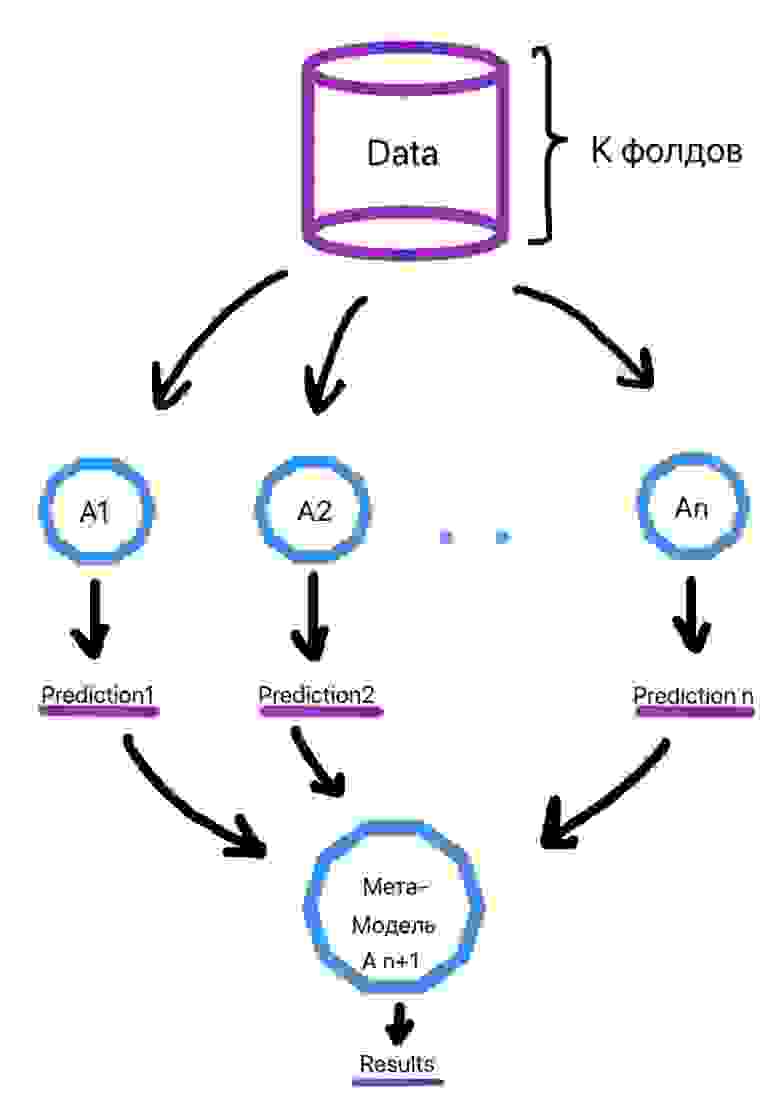
Ссылки на библиотеки для использования метода приведены ниже:

Бэггинг

Бэггинг является уже более популярным подходом и зачастую при упоминании этого термина вспоминается алгоритм построения случайного леса, как наиболее типичного его представителя.

При данном методе базовые алгоритмы являются представителями одного и того же семейства, они обучаются параллельно и почти независимо друг от друга, а финальные результаты лишь агрегируются. Нам необходимо, чтобы на вход слабым алгоритмам подавались разные данные, а не один и тот же набор, ведь тогда результат базовых моделей будет идентичен и смысла в них не будет.

0.632*n разных объектов. Таким образом, должны сформироваться m обучающих выборок для m слабых алгоритмов.

Бутстрэп выборки являются в значительной степени независимыми. Отчасти поэтому и говорят, что базовые алгоритмы обучаются на выборках независимо.

Что касается агрегации выходов базовых алгоритмов, то в случае задачи классификации зачастую просто выбирается наиболее часто встречающийся класс, а в случае задачи регрессии выходы алгоритмов усредняются (рис. 3). В формуле под ai подразумеваются выходы базовых алгоритмов.

Рисунок 3

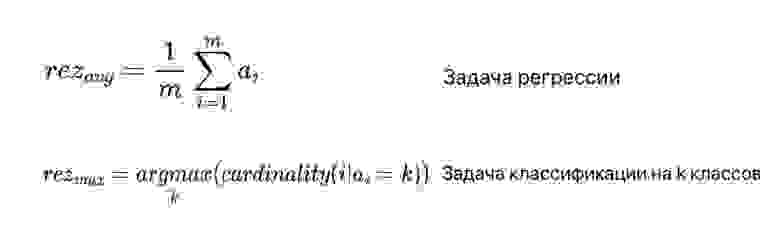
Общий процесс приведен на рисунке ниже (рис. 4):

Рисунок 4

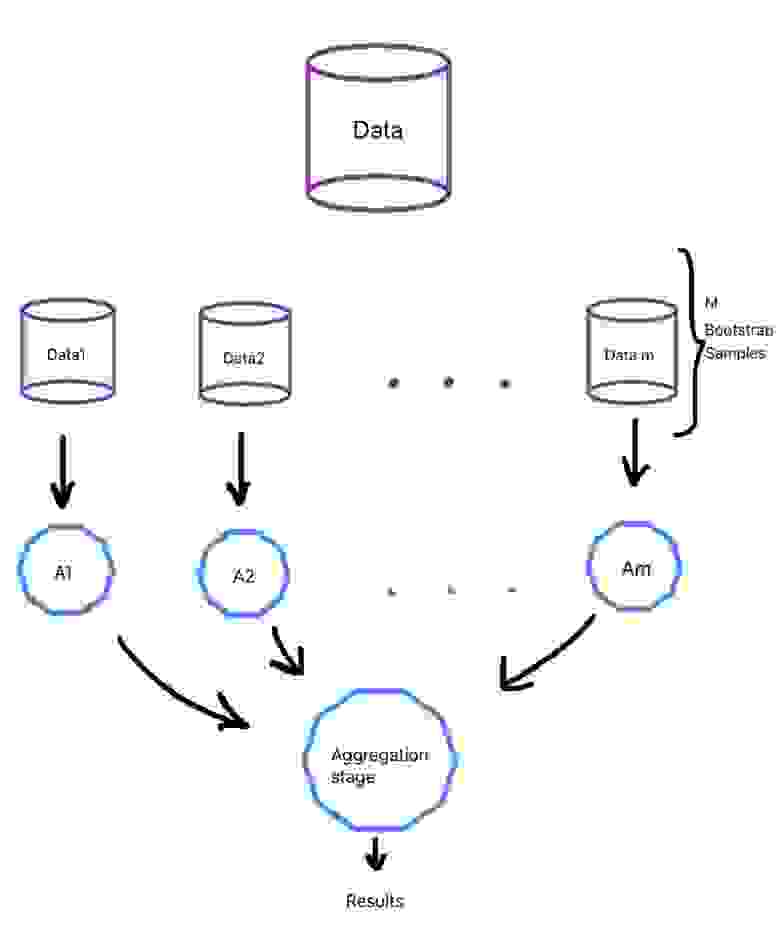
Случайный лес

Рисунок 5

Ссылки на библиотеки для использования метода приведены ниже:

Бустинг

В данном случае, модели уже не обучаются отдельно друг от друга, а каждая следующая правит ошибки предыдущей. То есть можно сказать, что если один слабый алгоритм не смог выявить какую-либо закономерность в данных, так как это было для него сложно, то следующая модель должна сделать это. Но из данного подхода вытекает недостаток: работу алгоритма трудно распараллелить из-за зависимости предыдущего и последующего шагов.

Бустинг направлен скорее на уменьшение смещения в данных, чем на снижение разброса в них. Поэтому в качестве базовых алгоритмов могут браться модели с достаточно высоким смещением, например, неглубокие случайные деревья.

Рисунок 6

Типичными представителями бустинга являются две модели: градиентный бустинг и AdaBoost. Обе по-разному решают одну и ту же оптимизационную задачу по поиску итоговой модели, представляющей собой взвешенную сумму слабых алгоритмов (рис. 6).

Градиентный бустинг использует типичный алгоритм градиентного спуска для решения задачи. Когда приходит время добавить новый слабый алгоритм в ансамбль делается следующее:

Находится оптимальный вектор сдвига, улучшающий предыдущий ансамбль алгоритмов.

Этот вектор сдвига является антиградиентом от функции ошибок работы предыдущего ансамбля моделей

Благодаря вектору сдвигов мы знаем, какие значения должны принимать объекты обучающей выборки

А поскольку нам надо найти очередной алгоритм в композиции, то находим тот, при использовании которого минимизируется отклонение ответов от истинных

Ссылки на библиотеки для использования метода приведены ниже:

Заключение

Таким образом, мы увидели, что для того, чтобы улучшить качество функционирования отдельно взятых моделей машинного обучения, существует ряд техник их объединения в ансамбли. Эти техники уже заложены в программные продукты и ими можно пользоваться, улучшая свое решение. Однако, с моей точки зрения, при решении задачи не стоит сразу же браться за них. Лучше сначала попробовать одну простую, отдельную модель, понять, как она функционирует на конкретных данных, а уже дальше использовать ансамбли.

Источник

Машинное обучение: ансамбль смешивания на Python

Смешивание — это ансамблевый алгоритм машинного обучения. Это разговорное название для стекового обобщения (stacked generalization) [далее будем использовать термин «пакетирование» вместо принятого в научных работах термина «стекинг»] или ансамбля пакетирования, где вместо того чтобы обучать метамодель на прогнозах вне групп, сделанных базовой моделью, модель обучается на прогнозах, сделанных на независимом наборе данных.

Обзор туториала

Этот туториал разделён на четыре части. Вот они:

Смешанный ансамбль

Смешивание — это метод ансамблевого машинного обучения, который использует модель машинного обучения, чтобы узнать, как наилучшим образом объединить прогнозы из нескольких моделей — участников ансамбля.

Таким образом, смешивание — это то же самое, что и стековое обобщение, известное как стекинг. Часто смешивание и пакетирование взаимозаменяемы используются в одной и той же статье или в описании модели.

Многие практики машинного обучения добились успеха, используя пакетирование и связанные с ним методы для повышения точности прогнозирования в сравнении с любой из отдельных моделей. В некоторых контекстах пакетирование также называется смешиванием. Здесь мы также будем взаимозаменять термины.
Feature-Weighted Linear Stacking, 2009.

Архитектура пакетированной модели содержит две или более базовых моделей, часто называемых моделями нулевого уровня, а метамодель, которая объединяет прогнозы базовых моделей, — моделью первого уровня. Метамодель обучается на основе прогнозов, сделанных базовыми моделями на данных вне выборки.

Наше решение с RMSE=0,8643^2 представляет собой линейное смешение из более чем 100 результатов. [… ] На протяжении всего описания методов мы выделяем конкретные предикторы, которые участвовали в окончательном смешанном решении.
The BellKor 2008 Solution to the Netflix Prize, 2008.

Таким образом, смешивание — это разговорный термин для ансамблевого обучения с модельной архитектурой типа пакетирования. Он редко, если вообще когда-нибудь, используется в учебниках или научных работах, кроме тех, которые связаны с машинным обучением на соревнованиях. Чаще всего термин «смешивание» используется для описания специфического применения пакетирования, когда метамодель обучается на прогнозах, сделанных базовыми моделями с независимым набором данных валидации. В этом контексте пакетирование зарезервировано для метамодели, обучаемой на прогнозах во время процедуры кросс-валидации.

Смешивание — это слово, введённое победителями Netflix. Оно очень близко к обобщению, но немного проще и риск утечки информации меньше. [… ] С помощью смешивания, вместо того чтобы создавать прогнозы во время кросс-валидации для тренировочного набора, вы создаёте небольшой независимый набор, скажем, 10% от тренировочного. Затем модель пакетирования тренируется только на этом небольшом наборе.
Kaggle Ensemble Guide, MLWave, 2015.

Мы используем последнее определение смешивания. Давайте посмотрим, как оно реализуется.

Разработка смешанного ансамбля

Библиотека scikit-learn не поддерживает смешивание из коробки на момент написания статьи. Но мы можем реализовать его самостоятельно, используя модели scikit-learn. Во-первых, нужно создать ряд базовых моделей. Это могут быть любые модели, которые нам нравятся в задаче регрессии или классификации. Мы можем определить функцию get_models(), которая возвращает список моделей, где каждая модель определяется как кортеж с названием и настроенным классификатором или объектом регрессии. Например, для задачи классификации мы могли бы использовать логистическую регрессию, kNN, дерево решений, SVM и наивную байесовскую модель.

Далее нам нужно обучить смешивающую модель. Напомним, что базовые модели обучаются на тренировочном наборе данных. Метамодель обучается на прогнозах, сделанных каждой базовой моделью на независимом наборе данных.

Во-первых, мы можем в цикле перечислить модели в списке и обучить каждую из них по очереди на обучающем наборе данных. Кроме того, в этом цикле мы можем использовать обученную модель, чтобы сделать прогноз на независимом наборе данных (валидации) и сохранить прогнозы на будущее.

Теперь у нас есть «meta_X*», представляющий входные данные, которые могут использоваться для обучения метамодели. Каждый столбец или объект представляет выходные данные одной базовой модели. Каждая строка представляет собой один сэмпл из независимого набора данных. Мы можем применить функцию hstack() чтобы гарантировать, что этот набор данных представляет собой двумерный массив numpy, как и ожидалось моделью машинного обучения.

Теперь мы можем тренировать нашу метамодель. Это может быть любая модель машинного обучения, которая нам нравится, например логистическая регрессия для задачи классификации.

Можно объединить всё это вместе в функцию с именем fit_ensemble(), которая обучает смешивающую модель с использованием обучающего и независимого набора данных валидации.

Следующий шаг — использование смешивающего ансамбля для прогнозирования новых данных. Это двухэтапный процесс. Первый шаг — использование каждой базовой модели для прогнозирования. Затем прогнозы собираются вместе и используются в качестве входных данных для модели смешивания, чтобы сделать окончательный прогноз.

Мы можем использовать тот же цикл, что и при обучении модели. То есть собрать прогнозы каждой базовой модели в обучающий набор данных, сложить прогнозы вместе и вызвать predict() в смешивающей модели с этим набором данных метауровня. Функция predict_ensemble() ниже реализует эти действия. Учитывая обучение списка базовых моделей, обучение смешивателя ансамбля и набор данных (например, тестовый набор данных или новые данные), для набора данных она вернёт набор прогнозов.

Теперь у нас есть все элементы, необходимые для реализации смешанного ансамбля для задач классификации или регрессионного прогностического моделирования.

Смешанный ансамбль для задачи классификации

В этом разделе мы рассмотрим использование смешивания для задачи классификации. Во-первых, мы можем использовать функцию make_classification(), чтобы создать синтетическую задачу бинарной классификации с 10 000 примерами и 20 входными признаками. Весь пример приведён ниже.

Запуск примера создаёт набор данных и резюмирует входные и выходные данные.

Далее нам нужно разделить набор данных сначала на обучающие и тестовые наборы, а затем обучающий набор на подмножество, используемое для обучения базовых моделей, и подмножество, используемое для обучения метамодели. В этом случае мы будем использовать разделение 50-50 для тренировочного и тестового наборов, а затем — разделение 67-33 для тренировочного набора и набора валидации.

Затем можно использовать функцию get_models() из предыдущего раздела для создания используемых в ансамбле классификационных моделей. После функция fit_ensemble() может быть вызвана для обучения смешанного ансамбля на этих наборах данных, а функция predict_ensemble() может использоваться для прогнозов на независимом наборе данных.

Наконец, мы можем оценить производительность модели смешивания, сообщив о точности классификации в тестовом наборе данных.

Полный пример оценки смешанного ансамбля в задаче синтетической бинарной классификации приведён ниже.

Запуск примера сначала сообщает резюме всех наборов данных, а затем точность ансамбля в тестовом наборе данных.

Примечание: ваши результаты могут различаться с учётом стохастического характера алгоритма или процедуры оценки, или различий в числовой точности. Подумайте о том, чтобы запустить пример несколько раз и сравнить средний результат.

Здесь мы видим, что смешанный ансамбль достиг точности классификации около 97,900%.

В предыдущем примере прогноз чётких меток классов был объединён с помощью модели смешивания. Это тип жёсткого голосования. Альтернатива — метод, когда каждая модель прогнозирует вероятности классов и использует метамодель для смешивания вероятностей. Это своего рода мягкое голосование, которое иногда может привести к повышению производительности. Во-первых, мы должны сконфигурировать модели, возвращающие вероятности, такие как модель SVM.

Затем нужно изменить базовые модели, чтобы вместо чётких меток классов прогнозировать вероятности. Это может быть достигнуто вызовом функции predict_proba () внутри функции fit_ensemble() при обучении базовых моделей.

Это означает, что мета-набор данных, используемый для обучения мета-модели, будет иметь n столбцов на классификатор, где n — количество классов в задаче прогнозирования, в нашем случае классов два. Нам также необходимо изменить прогнозы, сделанные базовыми моделями, при использовании смешивающей модели для прогнозирования новых данных.

Весь пример использования смешивания на спрогнозированных вероятностях классов для задачи синтетической бинарной классификации приведён ниже.

Запуск примера сначала сообщает резюме всех наборов данных, а затем точность ансамбля в тестовом наборе.

Примечание: ваши результаты могут различаться, учитывая стохастический характер алгоритма или процедуры оценки, или различия в числовой точности. Попробуйте выполнить пример несколько раз и сравнить средний результат.

Здесь видим, что смешение вероятностей классов привело к повышению точности классификации примерно до 98,240 %.

Смешанный ансамбль эффективен только в том случае, если он способен превзойти любую из отдельных моделей в нём. Мы можем подтвердить это, оценив каждую из базовых моделей в отдельности. Каждая базовая модель может быть обучена на всём обучающем наборе данных (в отличие от ансамбля смешивания) и оценена на тестовом наборе данных (так же, как в ансамбле смешивания). Пример ниже демонстрирует это, оценивая каждую базовую модель в отдельности.

Запуск примера сначала сообщает резюме всех трёх наборов данных, а затем точность каждой базовой модели в тестовом наборе.

Примечание: ваши результаты могут отличаться учитывая стохастический характер алгоритма, или процедуру оценки, или различия в числовой точности. Попробуйте выполнить пример несколько раз и сравнить средний результат.

В этом случае мы видим, что все модели работают хуже смешанного ансамбля. Интересно вот что: мы видим, что SVM очень близок к достижению точности 98,200 % по сравнению с точностью 98,240 %, достигнутой с помощью смешанного ансамбля.

Мы можем выбрать смешанный ансамбль в качестве нашей окончательной модели. Это включает обучение ансамбля на всём тренировочном наборе данных и составление прогнозов на новых примерах. В частности, весь обучающий набор разбивается на обучающие и валидационные наборы для обучения базовой и метамодели соответственно, а затем ансамбль может использоваться в прогнозировании. Полный пример составления прогноза по новым данным с использованием смешанного ансамбля для классификации выглядит так:

Запуск примера обучает модель смешанного ансамбля в наборе данных и затем используется для прогнозирования новой строки данных, как это было бы при использовании модели в приложении.

Давайте рассмотрим, как мы могли бы оценить смешанный ансамбль для регрессии.

Смешанный ансамбль для задачи регрессии

В этом разделе мы рассмотрим использование пакетирования для регрессионной задачи. Во-первых, мы можем использовать функцию make_regression(), чтобы создать синтетическую регрессионную задачу с 10 000 сэмплов и 20 входными признаками. Весь пример приведен ниже.

Запуск примера создаёт набор данных и резюмирует входные и выходные компоненты.

Далее можно определить список регрессионных моделей для применения в качестве базовых. В этом случае используем линейную регрессию, kNN, дерево решений и модели SVM.

Функция fit_ensemble(), используемая для обучения ансамбля, не изменяется, за исключением того, что модель, используемая для смешивания, должна быть изменена на регрессионную. Здесь используем модель линейной регрессии.

Учитывая, что это задача регрессии, мы будем оценивать производительность модели с помощью метрики ошибок, в данном случае средней абсолютной ошибки, или (сокращённо) MAE.

Весь пример смешанного ансамбля для задачи прогнозного моделирования синтетической регрессии приведён ниже:

Пример сначала выводит резюме трёх наборов данных, а затем MAE на тестовом наборе.

Примечание: ваши результаты могут различаться, учитывая стохастический характер алгоритма или процедуры оценки, или различия в числовой точности. Попробуйте выполнить пример несколько раз и сравнить средний результат.

Здесь видим, что ансамбль достиг MAE около 0,237 на тестовом наборе данных.

Как и в случае с классификацией, смешанный ансамбль полезен только в том случае, если он работает лучше, чем любая из базовых моделей ансамбля.

Мы можем проверить это, оценив каждую базовую модель изолированно, сначала обучив ее на обучающем наборе целиком (в отличие от ансамбля) и сделав прогнозы на тестовом наборе данных (как в ансамбле). В приведённом ниже примере каждая из базовых моделей оценивается изолированно на основе набора данных синтетического регрессионного прогностического моделирования.

Запуск примера сначала резюмирует тренировочный и тестовый наборы, а затем MAE каждой базовой модели в тестовом наборе данных.

Примечание: ваши результаты могут различаться, учитывая стохастический характер алгоритма или процедуры оценки, или различия в числовой точности. Попробуйте выполнить пример несколько раз и сравнить средний результат.

Здесь видно, что на самом деле линейная регрессионная модель показала себя немного лучше, чем смешанный ансамбль, достигнув MAE 0,236 по сравнению с 0,237. Это может быть связано с тем, как был построен синтетический набор данных.

Тем не менее в этом случае мы предпочли бы использовать линейную регрессионную модель именно для этой задачи. Ситуация подчёркивает важность проверки производительности вносящих вклад моделей, прежде чем принимать ансамблевую модель как окончательную.

Опять же, можно применять смешанный ансамбль в качестве окончательной модели регрессии. Подход включает разбиение всего набора данных на обучающий и тестовый наборы, чтобы на них обучить базовую и метамодели соответственно, затем ансамбль можно использовать для прогнозирования новой строки данных. Весь пример составления прогноза по новым данным с помощью смешанного ансамбля для задачи регрессии приведён ниже.

Запуск примера обучает модели ансамбля на наборе данных и затем используется для прогнозирования новой строки данных, как это было бы при использовании модели в приложении.

И не забывайте про промокод HABR, добавляющий 10% к скидке на баннере.

Источник

Анализ малых данных

КвазиНаучный блог Александра Дьяконова

Ансамбли в машинном обучении

В этом блоге было уже много постов про разные частные случаи ансамблей. Теперь просто их общая систематизация (точнее, вступительная часть в повествовании про ансамблирование), в результате которой получится самый подробный обзор про ансамблирование в рунете;)

Ансамблем (Ensemble, Multiple Classifier System) называется алгоритм, который состоит из нескольких алгоритмов машинного обучения, а процесс построения ансамбля называется ансамблированием (ensemble learning). Простейший пример ансамбля в регрессии – усреднение нескольких алгоритмов:

Алгоритмы из которых состоит ансамбль (в (1) – b_t) называются базовыми алгоритмами (base learners). Если рассматривать значения базовых алгоритмов на объекте как независимые случайные величины с одинаковым матожиданием и одинаковой конечной дисперсией, то понятно, что случайная величина (1) имеет такое же матожидание, но меньшую дисперсию:

Замечание. Требование равенства матожиданий ответов базовых алгоритмов вполне естественное: если мы берём алгоритмы из несмещённой модели, то их матожидания не только совпадают, но и равны значению истинной метки. А вот у требования равенства дисперсий уже нет приемлемого оправдания, но для обоснования эффективности ансамбля можно потребовать меньше… вопрос: что именно?

В задачах классификации простейший пример ансамбля – комитет большинства:

где mode – мода (значение, которое встречается чаще других среди аргументов функции). Если рассмотреть задачу классификации с двумя классами и три алгоритма, каждый из которых ошибается с вероятностью p, то в предположении, что их ответы – независимые случайные величины, получаем, что комитет большинства этих трёх алгоритмов ошибается с вероятностью pp(3-2p). Как видно на рис. 1, это выражение может быть существенно меньше p (при p=0.1 почти в два раза), т.е. использование такого ансамбля уменьшает ошибку базовых алгоритмов.

Рис 1. График вероятности ошибки комитета большинства.

Замечание. Если рассмотреть большее число алгоритмов, то по неравенству Хёфдинга ошибка комитета большинства

т.е. она экспоненциально убывает с ростом числа базовых алгоритмов.

Замечание. Наше теоретическое обоснование не совсем годится для реальной практической ситуации, поскольку регрессоры/классификаторы не являются независимыми:

Поэтому большинство приёмов в прикладном ансамблировании направлено на то, чтобы ансамбль был «достаточно разнообразным», тогда ошибки отдельных алгоритмов на отдельных объектах будут компенсироваться корректной работой других алгоритмов. По сути, при построении ансамбля:

Как будет показано дальше, разнообразие повышают за счёт (в скобках указаны примеры, где применяется соответствующий приём):

Приведём примеры естественного (уже реализовано в модели) и искусственного (ручного) варьирования в рамках одной модели. При обучении нейросетей многое может зависеть от начальной инициализации параметров, поэтому даже при использовании одной и той же архитектуры нейросети после двух разных процедур обучения мы можем получить разные алгоритмы. Ручное варьирование достигается принудительным фиксированием некоторых параметров алгоритма, например, можно делать бустинг над решающими деревьями глубины 1, 2, 3 и т.д., а потом ансамблировать полученные алгоритмы (они будут различными, хотя формально мы использовали одну модель).

Ещё один довод в пользу разнообразия алгоритмов в ансамбле можно привести с помощью такого эксперимента. Будем бинарным вектором кодировать правильные ответы алгоритма на контрольной выборке в задаче с двумя классами: 1 – правильный ответ, 0 – ошибка. Если мы построим несколько одинаковых алгоритмов (по крайней мере, в смысле совпадения указанных характеристических векторов правильных ответов), то голосование по этим алгоритмам будет иметь точно такой же вектор:

Теперь построим похожие алгоритмы:

Теперь построим совершенно разные алгоритмы:

Как видно, ансамбль «совсем разнообразных» алгоритмов показал лучшее качество. Вопрос: нет ли подвоха в этом примере?

В общем случае ансамбль записывается как

где b – некоторый алгоритм (т.е. функция), который принято называть мета-алгоритмом (meta-estimator). Как видим, выражения (1) и (2) являются частным случаем этой записи.

Обоснования использования ансамблей в машинном обучении обычно бывают статистическими (statistical) – приведены выше, когда мы оценивали ошибку ансамбля исходя из вероятностной природы ответов алгоритмов, вычислительными (computational) – поскольку обучение это решение задачи оптимизации, то ансамбль распараллеливает процесс: мы параллельно обучаем несколько базовых алгоритмов, а метаалгоритм «комбинирует» полученные ответы, функциональными (representational) – часто ансамблем можно представить существенно более сложную функцию, чем любым базовым алгоритмом. Последнее можно проиллюстрировать следующим рис. 2: показана задача бинарной классификации, в которой нельзя настроить на 100%-е качество линейный алгоритм, но можно настроить простейший ансамбль линейных алгоритмов. Кстати, какой? Таким образом, ансамбли позволяют решать сложные задачи простыми моделями, усложнение решения для возможности хорошей настройки на данные происходит на уровне мета-алгоритма.

Рис. 2. Линейные классификаторы в задаче с нелинейной природой данных.

Существуют следующие основные модели ансамблирования:

модель или общая идея

описание и примеры

Построение независимых алгоритмов и их усреднение / голосование по ним, в том числе с помощью бэгинга и предварительной деформации ответов. Здесь же и обобщения бэгинга – случайные леса.

Специальные кодировки целевых значений и сведение решения задачи к решению нескольких задач. Один из самых популярных приёмов – ECOC (error-correcting output coding). Другой – настройка на разные деформации целевого признака.

построение метапризнаков – ответов базовых алгоритмов на объектах выборки, обучение на них мета- алгоритма

Построение суммы нескольких алгоритмов. Каждое следующее слагаемое строится с учётом ошибок предыдущих: AdaBoost, градиентный бустинг.

Эвристические способы комбинирования ответов базовых алгоритмов (с помощью визуализаций, обучения в специальных подпространствах и т.п.)