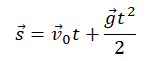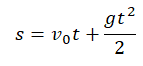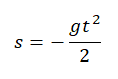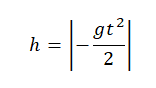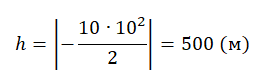Автомобиль движется равномерно и прямолинейно 560 м на протяжении 28 с затем начинает спуск

Тест №1 ЕГЭ по физике

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость автомобиля относительно земли ( v ₁), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v ₂). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

Алгоритм решения

Решение

Записываем данные относительно Земли:

Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость второго автомобиля относительно оси ОХ ( v ₂), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v ₁).

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид :

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Алгоритм решения

Решение

Записываем исходные данные:

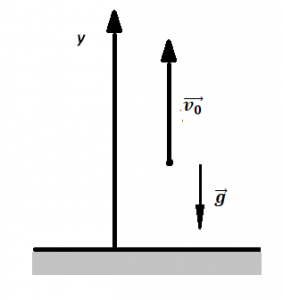
Записываем формулу для определения скорости тела в векторном виде:

Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:

Подставим известные данные и вычислим скорость:

Алгоритм решения

Решение

Записываем исходные данные:

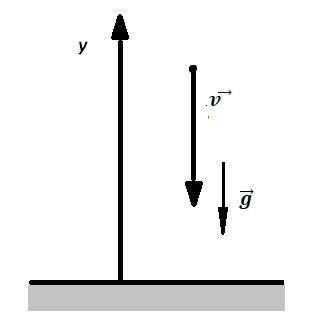
Перемещение (высота) свободно падающего тела, определяется по формуле:

В скалярном виде эта формула примет вид:

Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:

Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:

Вычисляем высоту, подставив известные данные:

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

Алгоритм решения

Решение

Записываем исходные данные:

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Источник

Контрольная работа по физике Прямолинейное движение 10 класс

Контрольная работа по физике Прямолинейное движение 10 класс с ответами. Контрольная работа включает 4 варианта, в каждом варианте по 9 заданий.

1 вариант

1. Сколько времени пассажир, сидящий у окна поез­да, идущего со скоростью 54 км/ч, будет видеть про­ходящий мимо него встречный поезд, скорость кото­рого 36 км/ч? Длина поезда 250 м.

2. Автомобиль движется со скорость 72 км/ч. Опреде­лите ускорение автомобиля, если через 20 с он остано­вится.

4. Теплоход проходит расстояние между двумя горо­дами вверх по течению реки за 80 ч, а вниз по течению за 60 ч. Определите время, за которое расстояние между городами проплывет плот.

5. При взлете самолет за 40 с приобретает скорость 300 км/ч. Какова длина взлетной полосы?

7. Эскалатор метро поднимает неподвижно стоящего на нем пассажира за 1 мин. По неподвижному эскала­тору пассажир поднимается за 3 мин. Сколько време­ни будет подниматься идущий пассажир по движуще­муся эскалатору?

8. Мяч, скатываясь с наклонной плоскости из состо­яния покоя, за первую секунду прошел путь 15 см. Определите путь, пройденный мячом за 2 с.

9. Тело движется равномерно со скоростью 3 м/с в те­чение 20 с, затем в течение 15 с движется с ускорени­ем 0,2 м/с 2 и останавливается. Найдите путь, прой­денный телом за все время движения.

2 вариант

1. Одновременно из пунктов А и В, расстояние между которыми равно 250 км, навстречу друг другу выеха­ли два автомобиля. Определите, через какое время встретятся автомобили, если их скорости соответ­ственно равны 60 км/ч и 40 км/ч.

3. Рассчитайте ускорение поезда, движущегося со ско­ростью 18 км/ч, если он, начав торможение, останав­ливается в течение 10 с.

4. Катер переправляется через реку. Скорость течения равна 3 м/с, скорость катера в стоячей воде — 6 м/с. Определите угол между векторами скорости катера от­носительно воды и скорости течения, если катер пере­плывает реку по кратчайшему пути.

5. Автомобиль, движущийся со скоростью 36 км/ч, начинает тормозить и останавливается через 2 с. Ка­ков тормозной путь автомобиля?

6. Чему равно ускорение пули, которая, пробив стену толщиной 35 см, уменьшила свою скорость с 800 до 400 м/с?

7. Первую треть пути велосипедист ехал со скоростью 15 км/ч. Средняя скорость велосипедиста на всем пу­ти равна 20 км/ч. С какой скоростью он ехал остав­шуюся часть пути?

8. Двигаясь из состояния покоя, автомобиль за первые 5 с проходит 25 м. Рассчитайте путь, пройденный ав­томобилем за десятую секунду после начала движе­ния.

9. При остановке автобус за последнюю секунду про­ехал половину тормозного пути. Каково полное время торможения автобуса?

3 вариант

1. Пассажир поезда, идущего со скоростью 15 м/с, ви­дит в окне встречный поезд длиной 150 м в течение 6 с. Какова скорость встречного поезда?

2. Автомобиль при разгоне за 10 с приобретает ско­рость 54 км/ч. Каково при этом ускорение автомо­биля?

4. За 1, 5 ч моторная лодка проходит против течения расстояние 18 км. За какое время она пройдет обрат­ный путь, если скорость течения равна 3 км/ч?

5. С каким ускорением двигался поезд до остановки, если в начале торможения он имел скорость 36 км/ч, а его тормозной путь равен 100 м?

6. Пройдя от станции расстояние 1,5 км, поезд развил скорость 54 км/ч. Каково время разгона поезда?

7. Катер, плывущий вниз по реке, догоняет спасатель­ный круг. Через 30 мин после этого катер поворачива­ет назад и снова встречает круг на расстоянии 5 км от места первой встречи. Найдите скорость течения ре­ки.

9. Найдите время, необходимое мотоциклисту для полной остановки, если за 3 с он проехал половину тормозного пути.

4 вариант

1. Из двух городов, расстояние между которыми рав­но 120 км, одновременно навстречу друг другу выеха­ли два автобуса, скорости которых постоянны и равны соответственно 20 км/ч и 60 км/ч. Через какое время встретятся автобусы?

4. Моторная лодка проходит расстояние между двумя пунктами по течению реки за 3 ч, а плот — за 12 ч. Сколько времени моторная лодка затратит на обрат­ный путь?

5. Определите время, за которое троллейбус, двигаясь из состояния покоя, на пути 500 м приобрел скорость 54 км/ч.

6. Двигаясь от остановки, тело достигло скорости 50 м/с, пройдя путь 50 м. Чему равно ускорение, с ко­торым двигалось тело?

7. Скорость поезда на подъеме равна 30 км/ч, а на спуске — 90 км/ч. Определите среднюю скорость на всем участке пути, если спуск в 2 раза длиннее подъ­ема.

8. За последнюю (пятую) секунду равнозамедленного движения тело проходит 5 ми останавливается. Чему равен путь, пройденный телом за третью секунду?

9. Расстояние 1,8 км между двумя станциями метро поезд проходит со средней скоростью 54 км/ч. На уча­стке разгона он движется равноускоренно в течение 40 с, затем едет равномерно, после чего равнозамед­ленно в течение 20 с до полной остановки. Определите наибольшую скорость поезда.

ОТВЕТЫ — Контрольная работа по физике Прямолинейное движение 10 класс
1 вариант
1. 10 с
2. 1 м/с 2
3. 10 с
4. 20 сут
5. 1667 м
6. 20 м/с
7. 45 с
8. 0,6 м
9. 82,5 м
2 вариант
1. 2,5 ч
2. 12 м/с
3. 0,5 м/с 2
4. 120°
5. 10 м
6. 7 · 10 5 м/с 2
7. 24 км/ч
8. 19 м
9. 1,41 с
3 вариант
1. 10 /с
2. 1,5 м/с 2
3. 158 с
4. 1ч
5. 0,5 м/с 2
6. 200 с
7. 5 км/ч
8. 198 м
9. 10 с
4 вариант
1. 1,5 ч
2. 50 с
3. 32,4 м
4. 6 ч
5. 67 с
6. 25 м/с 2
7. 54 км/ч
8. 25 м
9. 20 м/с

Источник

Автомобиль движется равномерно и прямолинейно 560 м на протяжении 28 с затем начинает спуск

Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение автомобиля по мосту.

1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.

2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.

3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.

5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.

Переведем скорость

Рассмотрим рисунок, поясняющий движение автомобиля по выпуклому мосту.

1. Неверно. Равнодействующая сил реакции опоры N и силы тяжести mg по второму закону Ньютона сонаправлена с вектором ускорения. А т. к. автомобиль движется по окружности, то ускорение направлено к центру окружности, т. е. вниз. Следовательно, и равнодействующая направлена вниз. Скорость автомобиля при движении по окружности направлена по касательной (в данном случае — горизонтально).

2. Неверно. Сила, с которой мост действует на автомобиль — сила реакции опоры — направлена вертикально вверх.

3. Верно. Сила, с которой автомобиль действует на мост, равна весу тела. По третьему закону Ньютона P = N. Найдём силу реакции опоры по второму закону Ньютона Центростремительное ускорение равно Значит, Р = 15 кН.

4. Верно. (см. пункт 3).

5. Неверно. Вектор ускорения направлен вертикально вниз, вектор скорости — горизонтально (см. пункт 1).

Источник

Автомобиль движется равномерно и прямолинейно 560 м на протяжении 28 с затем начинает спуск

Школьник летом на даче жил недалеко от военного аэродрома, на который постоянно садились военно-транспортные самолеты, которые летели всегда по одной и той же траектории («глиссаде»), проекция которой на землю являлась прямой линией, отстоящей на расстояние от дачи школьника. Он вооружился секундомером и точным угломерным инструментом, провел многократные измерения некоторых времен и углов и усреднил их для однотипных марок самолетов. Оказалось, что когда самолет находился на минимальном расстоянии от школьника, угол между горизонталью и направлением на самолет составлял а а звук его двигателей был слышен в месте нахождения школьника спустя время За это время самолет успевал удалиться от точки максимального сближения со школьником на угловое расстояние Исходя из этих данных, школьник определил скорость самолета. Чему она оказалась равна?

Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.

Обоснование. Движение самолета является поступательным, поэтому самолет можно считать материальной точкой и рассматривать перемещение в вертикальной плоскости. Учитывая, что промежуток времени очень мал, можно считать за данный интервал времени движение самолета прямолинейным и равномерным и применять законы данного вида движения.

Перейдем к решению. Поскольку угол наклона глиссады мал, то в момент максимального сближения самолета и школьника расстояние между ними примерно равно

где l — раcстояние до глиссады.

Звук от двигателей, излученный в этот момент, доходит до школьника, согласно условию, спустя время и школьник слышит максимум громкости.

За время t самолёт успевает удалиться от точки максимального сближения со школьником в направлении перпендикулярном L на расстояние, равное Таким образом, и скорость самолета

Источник