Чему равна по модулю скорость велосипедиста относительно автомобиля

По дорогам, пересекающимся под прямым углом, едут велосипедист и автомобилист?

По дорогам, пересекающимся под прямым углом, едут велосипедист и автомобилист.

Скорости велосипедиста и автомобилиста относительно придорожных столбов соответственно равны 8 м / с и 15 м / с.

Чему равен модуль скорости автомобилиста относительно велосипедиста?

V = корень(v₁² + v₂²) = корень((8 м / с)² + (15 м / с)²) = корень(64 + 225) = корень(289) = 17 м / с.

По дорогам, пересекающимся под прямым углом, едут велосипедист и автомобилист?

По дорогам, пересекающимся под прямым углом, едут велосипедист и автомобилист.

Скорости велосипедиста и автомобилиста относительно придорожных столбов соответственно равны 8 м / с и 15 м / с.

Чему равен модуль скорости автомобилиста относительно велосипедиста?

Автомобилист и велосипедист движутся навстречу друг другу?

Автомобилист и велосипедист движутся навстречу друг другу.

Найти зависимость x от t и построить график.

Какова скорость второго автомобиля относительно первого?

Два велосипедиста едут со скоростями 10, 8 км / ч и 14, 4 км / ч по взаимно перпендикулярной дороге?

Два велосипедиста едут со скоростями 10, 8 км / ч и 14, 4 км / ч по взаимно перпендикулярной дороге.

Чему равна их относительная скорость?

Скорость первого велосипедиста относительно второго 5 км / ч, а относительно Земли 20 км / ч?

Скорость первого велосипедиста относительно второго 5 км / ч, а относительно Земли 20 км / ч.

Определите скорость второго велосипедиста относительно Земли.

Скорость первого велосипедиста относительно второго 5 км / ч, а относительно Земли 20 км / ч?

Скорость первого велосипедиста относительно второго 5 км / ч, а относительно Земли 20 км / ч.

Определите скорость второго велосипедиста относительно Земли.

С какой скоростью движется автомобиль относительно велосипедиста, если : а) автомобиль движется навстречу автомобилисту Объясните, пожалуйста, как это «относительно»?

Я немного не понимаю.

Скорость велосипедиста равна 10 м / с а скорость встречного ветра 4 м / с?

Скорость велосипедиста равна 10 м / с а скорость встречного ветра 4 м / с.

Какова скорость ветра относительно велосипедиста?

Какой была скорость ветра относительно него если бы ветер попутным?

Автомобилист и велосипедист одновременно начинают движение по прямой из состояния покоя?

Автомобилист и велосипедист одновременно начинают движение по прямой из состояния покоя.

Через 4 секунды скорость автомобилиста оказалась вдвое больше велосипедиста.

Скорость одного велосипедиста относительно другого 10км / ч, а относительно земли 25км / ч?

Скорость одного велосипедиста относительно другого 10км / ч, а относительно земли 25км / ч.

Определите скорость второго велосипедиста относительно земли.

Источник

Чему равна по модулю скорость велосипедиста относительно автомобиля

Пешеход идет по прямолинейному участку дороги со скоростью 4 км/ч. Навстречу ему движется автобус со скоростью 40 км/ч. С какой скоростью (в км/ч) должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?

Обозначим искомую скорость велосипедиста через Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью а к автобусу — со скоростью

Приравняв эти две скорости, находим требуемую скорость велосипедиста:

Не совсем понял решение. Объясните пожалуйста, как решаются подобные задачи?

Самое полезное, что можно придумать в таких задачах — нарисовать картинку, на ней обозначить вектора скоростей всех тел относительно одной системы отсчета (в данном случае, относительно Земли). А потом из рисунка уже выписывать, чему равны модули скоростей одних тел, относительно других. Например, пешеход и велосипедист двигаются навстречу, а значит, скорость их сближения — это сумма их скоростей относительно Земли: . А вот автобус нагоняет велосипедиста, поэтом его скорость относительно велосипедиста равна . Смотрите внимательно на картинку и все поймете.

Хочу предложить другой способ решения:

1. Находим модуль скорости сближения пешехода и автобуса |v-10v|=9v.

2. Делим полученную скорость на 2, т. к. модуль скорости велосипедиста должен быть одинаков относительно пешехода и автобуса ОДНОВРЕМЕННО, т. е. 4,5v.

Судя по картинке, скорость велосипедиста относительно пешехода равна 14 км/ч, а относительно автобуса — 22 км/ч. В условии сказано, чтобы скорости велосипедиста относительно двух тел (пешехода и автобуса) должны быть равны. Так вот, они (скорости) будут равны, если скорость велосипедиста относительно поверхности будет равна 22 км/ч. Пожалуйста, не говорите, что я неправильно решил задачу))

Скорость ве­ло­си­пе­ди­ста от­но­си­тель­но пе­ше­хо­да 18 + 4 = 22 км/ч такая же как относительно автобуса. Если тела движутся в разные стороны, то относительная скорость равна сумме скоростей, а не разности. Допустим, если два пешехода идут навстречу друг другу, то они сближаются со скоростью 4 + 4 = 8 км/ч, а не покоятся относительно друг друга (4 – 4 = 0).

Источник

Чему равна по модулю скорость велосипедиста относительно автомобиля

Пешеход идет по прямолинейному участку дороги со скоростью 4 км/ч. Навстречу ему движется автобус со скоростью 40 км/ч. С какой скоростью (в км/ч) должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?

Обозначим искомую скорость велосипедиста через Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью а к автобусу — со скоростью

Приравняв эти две скорости, находим требуемую скорость велосипедиста:

Не совсем понял решение. Объясните пожалуйста, как решаются подобные задачи?

Самое полезное, что можно придумать в таких задачах — нарисовать картинку, на ней обозначить вектора скоростей всех тел относительно одной системы отсчета (в данном случае, относительно Земли). А потом из рисунка уже выписывать, чему равны модули скоростей одних тел, относительно других. Например, пешеход и велосипедист двигаются навстречу, а значит, скорость их сближения — это сумма их скоростей относительно Земли: . А вот автобус нагоняет велосипедиста, поэтом его скорость относительно велосипедиста равна . Смотрите внимательно на картинку и все поймете.

Хочу предложить другой способ решения:

1. Находим модуль скорости сближения пешехода и автобуса |v-10v|=9v.

2. Делим полученную скорость на 2, т. к. модуль скорости велосипедиста должен быть одинаков относительно пешехода и автобуса ОДНОВРЕМЕННО, т. е. 4,5v.

Судя по картинке, скорость велосипедиста относительно пешехода равна 14 км/ч, а относительно автобуса — 22 км/ч. В условии сказано, чтобы скорости велосипедиста относительно двух тел (пешехода и автобуса) должны быть равны. Так вот, они (скорости) будут равны, если скорость велосипедиста относительно поверхности будет равна 22 км/ч. Пожалуйста, не говорите, что я неправильно решил задачу))

Скорость ве­ло­си­пе­ди­ста от­но­си­тель­но пе­ше­хо­да 18 + 4 = 22 км/ч такая же как относительно автобуса. Если тела движутся в разные стороны, то относительная скорость равна сумме скоростей, а не разности. Допустим, если два пешехода идут навстречу друг другу, то они сближаются со скоростью 4 + 4 = 8 км/ч, а не покоятся относительно друг друга (4 – 4 = 0).

Источник

Относительное движение

Скорость точки относительно неподвижной системы отсчета равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы.

\(v\) — абсолютная скорость

\(\vec\) — переносная скорость

\(v’\) — относительная скорость

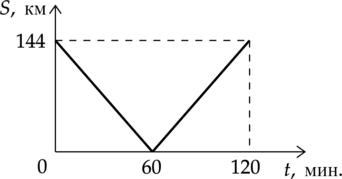
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?

За 60 минут расстояние между автомобилями изменилось с 144 км до 0 км, то есть автомобили встретились. Вычислим скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем: \[v=\dfrac<144000\text< м>><3600\text< с>>=40\text< м/с>\]

Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)

Так как пассажир идет в том же направлении, что и автобус, то вектора их скоростей складываются, поэтому абсолютная скорость равна \[\upsilon_<\text<абс>>=\upsilon_<\text<пер>>+\upsilon_<\text<отн>>=10\text< м/с>+1\text< м/с>=11\text< м/с>\]

По прямой дороге с постоянной скоростью 100 км/ч едет мотоциклист и в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)

Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 8 км/ч. Река течёт со скоростью 6 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.

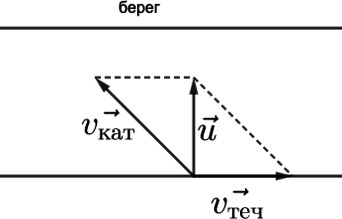
Чтобы катер двигался перпендикулярно относительно берега, относительно воды ему надо двигаться под углом. По закону сложения скоростей: \[\vec>>=\vec>>+\vec>>\] \[\vec=\vec>>+\vec>>\]
По теореме Пифагора найдем скорость катера относительно воды: \[v_<\text<кат>>=\sqrt>^2>=\sqrt<8^2+6^2>=10 \text< км/ч>\]

Пассажир зашел в автобус через заднюю дверь. Автобус поехал с постоянной скоростью \(\upsilon_1=25\) м/с, а пассажир пошел к передней части автобуса. Скорость пассажира относительно автобуса равна \(\upsilon_<2>=3\) м/с. С какой скоростью едет автобус относительно пассажира?

Скорость первого тела относительного второго равна скорости второго тела относительно первого и направлена в противоположную сторону. \[\vec_<\text<абс>>=\vec_<\text<отн>>+\vec_<\text<пер>>\] \[\vec_<\text<1>>=\vec_<\text<12>>+\vec_<\text<2>>\] \[\vec_<\text<2>>=\vec_<\text<21>>+\vec_<\text<1>>\] \[\vec_<\text<12>>=-\vec_<\text<21>>\] Таким образом, автобус относительно пассажира едет со скоростью 3 м/с в обратную сторону.

Источник

10класс. Равномерное движение. Относительность движения(профиль)

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

10 кл. Профиль.Равномерное движение, относительность движения

На рисунке представлен график зависимости пути S велосипедиста от времени t.

Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью

Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась

На других интервалах скорость была иная.

Правильный ответ указан под номером 4.

На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.

Пункт A находится в точке а пункт Б — в точке Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)

Для того чтобы по графику зависимости координаты от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Максимальной скорости соответствует максимальный угол наклона. Из приведенного графика видно, что с максимальной скоростью автобус движется из пункта A в пункт Б, скорость его при этом равна

На рисунке приведен график зависимости проекции скорости тела от времени.

Чему равно ускорение тела в интервале времени от 30 до 40 с? (Ответ дайте в метрах в секунду в квадрате.)

Из графика видно, что в интервале времени от 30 до 40 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.

Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)

Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки: Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение:

Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)

Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: То есть, буквально, надо весь пройденный телом путь разделить на всё время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.

Разберёмся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.

Вычислим теперь среднюю путевую скорость. Обозначим расстояние между двумя пунктами через тогда весь путь, пройденный велосипедистом, равен На первую половину пути велосипедист затратил время На обратную дорогу — время Всё время пути составило Окончательно, находим, что средняя путевая скорость велосипедиста равна

Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)

Из графика видно, что начальная координата тела равна Модуль перемещения тела относительно исходной точки в любой момент определяется выражением: Построим график этой функции и определим ее максимум. Из построенного графика ясно, что модуль перемещения относительно исходной точки максимален при и равен 20 м.

Движение двух велосипедистов задано уравнениями и Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)

Встреча двух велосипедистов означает, что у них в некоторый момент времени совпадут координаты. Определим, когда именно произойдет встреча, для этого решим уравнение Теперь не составляет труда определить координату места встречи:

На рисунке приведен график движения x(t) электрокара. Определите по этому графику путь, проделанный электрокаром за интервал времени от t₁ = 1 c до t₂ = 4 c. (Ответ дайте в метрах.)

Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. Из графика видно, что в интервале времени от 1 до 3 с электрокар двигался в положительном направлении оси При этом его координата изменилась на Последнюю, четвертую, секунду электрокар двигался в обратном направлении, изменение его координаты на этом участке равно Таким образом, путь, пройденный машинкой за интервал времени от 1 до 4 с равен

Пешеход идет по прямолинейному участку дороги со скоростью 4 км/ч. Навстречу ему движется автобус со скоростью 40 км/ч. С какой скоростью (в км/ч) должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?

Обозначим искомую скорость велосипедиста через Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью а к автобусу — со скоростью

Приравняв эти две скорости, находим требуемую скорость велосипедиста:

Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)

Обозначим искомую скорость течения реки через а скорость парохода в стоячей воде — через Тогда можно составить следующие уравнения. Скорость парохода вниз по течению равна Скорость парохода вверх по течению: Решая систему из двух этих уравнений, для скорости течения воды имеем

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. На какую величину Δv скорость второго тела v₂ больше скорости первого тела v₁? (Ответ дайте в метрах в секунду.)

Из графика видно, что для обоих тел пройденный путь линейно зависит от времени, а значит, оба тела двигались с постоянными по величине скоростями. Модуль скорости первого тела равен Скорость же второго тела: Следовательно, скорость второго тела больше скорости первого тела на величину

Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)

Используя график, определим проекции скоростей обоих тел. Для тела 1 имеем

Таким образом модуль скорости одного тела относительно другого равен

Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)

Согласно закону сложения скоростей, скорость тела относительно «неподвижной системы отсчёта» связана со скоростью этого тела относительно «подвижной системы отсчёта» и скоростью движения «подвижной с. о.» относительно «неподвижной» при помощи следующего соотношения: В данном случае, так как пассажир двигается вдоль автобуса по направлению его движения, для скорости пассажира относительно дороги имеем:

Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)

Перейдём в систему отсчёта, связанную с автомобилем. Модуль скорости движения мотоцикла в данной системе отсчёта будет равен 50 + 70 = 120 км/ч.

Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)

Перейдём в систему отсчёта, связанную с автомобилем. Модуль скорости движения мотоцикла в данной системе отсчёта будет равна |50 − 70| = 20 км/ч.

На рисунке представлен график зависимости пути S велосипедиста от времени t. Найдите скорость велосипедиста в интервале времени от 50 до 70 с.

За время от 50 до 70 с велосипедист проехал 250 − 100 = 150 м, значит, его скорость равна 150 м : 20 с = 7,5 м/с.

На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наибольший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.

Из графика видно, что координата на каждом отдельном интервале времени изменяется линейно, следовательно, движение на каждом участке происходит с постоянной скоростью. Проекцию скорости велосипедиста на ось x на каждом интервале времени можно определить разделив разность координат в начале и в конце интервала на длительность интервала времени.

Интервал от 0 до 10 с:

Интервал от 10 до 30 с:

Интервал от 30 до 50 с:

Интервал от 50 до 70 с:

Наибольший модуль скорости составляет 10 м/с.

На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наименьший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.

Из графика видно, что координата на каждом отдельном интервале времени изменяется линейно, следовательно, движение на каждом участке происходит с постоянной скоростью. Проекцию скорости велосипедиста на ось x на каждом интервале времени можно определить разделив разность координат в начале и в конце интервала на длительность интервала времени.

Интервал от 0 до 10 с:

Интервал от 10 до 30 с:

Интервал от 30 до 50 с:

Интервал от 50 до 70 с:

Наименьший модуль скорости составляет 2,5 м/с.

На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наибольший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.

Из графика видно, что координата на каждом отдельном интервале времени изменяется линейно, следовательно, движение на каждом участке происходит с постоянной скоростью. Проекцию скорости велосипедиста на ось x на каждом интервале времени можно определить разделив разность координат в начале и в конце интервала на длительность интервала времени.

Интервал от 0 до 10 с:

Интервал от 10 до 30 с:

Интервал от 30 до 50 с:

Интервал от 50 до 70 с:

Наибольший модуль скорости составляет 10 м/с.

На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наименьший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.

Из графика видно, что координата на каждом отдельном интервале времени изменяется линейно, следовательно, движение на каждом участке происходит с постоянной скоростью. Проекцию скорости велосипедиста на ось x на каждом интервале времени можно определить разделив разность координат в начале и в конце интервала на длительность интервала времени.

Интервал от 0 до 10 с:

Интервал от 10 до 30 с:

Интервал от 30 до 50 с:

Интервал от 50 до 70 с:

Наименьший модуль скорости составляет 2,5 м/с.

Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.

Вектор скорости катера относительно воды разложим на две компоненты: где вектор направлен параллельно берегу, а вектор — перпендикулярно берегу. Для того чтобы катер в системе отсчёта, связанной с берегом, двигалась перпендикулярно к нему, необходимо, чтобы компонента скорости катера относительно воды вдоль реки в точности компенсировала скорость течения Тогда модуль скорости катера относительно воды будет равен (по теореме Пифагора)

Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 4,8 км/ч. Река течёт со скоростью 3,6 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.

Вектор скорости катера относительно воды разложим на две компоненты: где вектор направлен параллельно берегу, а вектор — перпендикулярно берегу. Для того, чтобы катер в системе отсчета, связанной с берегом, двигалась перпендикулярно к нему, необходимо, чтобы компонента скорости катера относительно воды вдоль реки в точности компенсировала скорость течения u. Тогда модуль скорости катера относительно воды будет равен (по теореме Пифагора)

Источник