что показывает auc roc
Глубокое погружение в ROC-AUC
Я думаю, что большинство людей слышали о ROC-кривой или о AUC (площади под кривой) раньше. Особенно те, кто интересуется наукой о данных. Однако, что такое ROC-кривая и почему площадь под этой кривой является хорошей метрикой для оценки модели классификации?
Теория ROC-кривой
Полное название ROC — Receiver Operating Characteristic (рабочая характеристика приёмника). Впервые она была создана для использования радиолокационного обнаружения сигналов во время Второй мировой войны. США использовали ROC для повышения точности обнаружения японских самолетов с помощью радара. Поэтому ее называют рабочей характеристикой приемника.
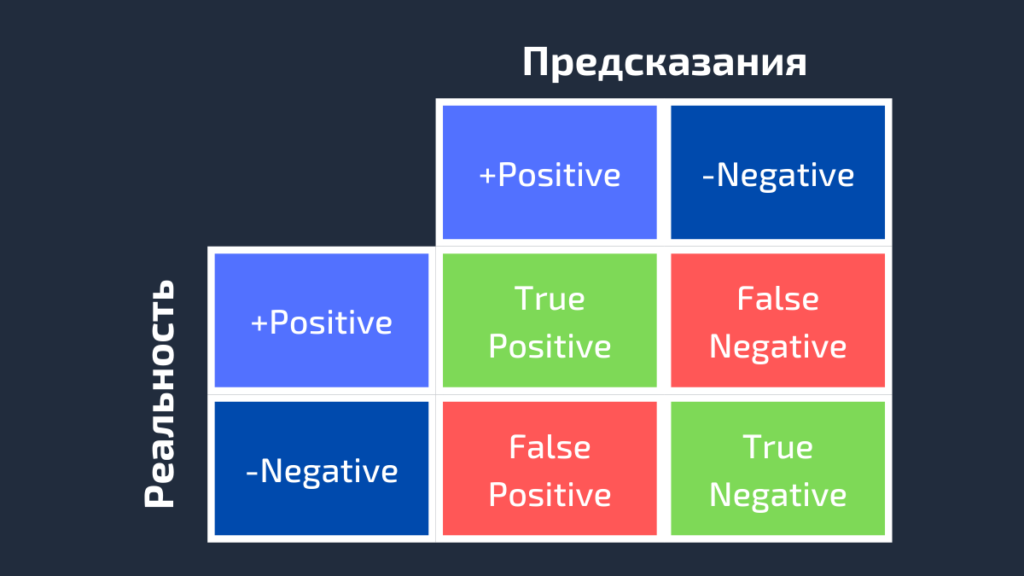
AUC или area under curve — это просто площадь под кривой ROC. Прежде чем мы перейдем к тому, что такое ROC-кривая, нужно вспомнить, что такое матрица ошибок.
Как видно из рисунка выше, матрица ошибок — это комбинация вашего прогноза (1 или 0) и фактического значения (1 или 0). В зависимости от результата предсказания и того, корректна ли была проведена классификация, матрица разделена на 4 части. Например, true positive (истинно положительный) результат — это количество случаев, в которых вы правильно классифицируете семпл как положительный. А false positive (ложноположительный) — это число случаев, в которых вы ошибочно классифицируете семпл как положительный.
Матрица ошибок содержит только абсолютные числа. Однако, используя их, мы можем получить множество других метрик, основанных на процентных соотношениях. True Positive Rate (TPR) и False Positive Rate (FPR) — две из них.
True Positive Rate (TPR) показывает, какой процент среди всех positive верно предсказан моделью.
TPR = TP / (TP + FN).
False Positive Rate (FPR): какой процент среди всех negative неверно предсказан моделью.
FPR = FP / (FP + TN).
Хорошо, давайте теперь перейдем к кривой ROC!
Что такое ROC-кривая?
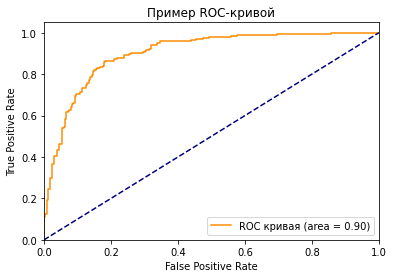
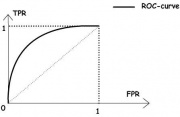
Как вы можете видеть на графике, кривая ROC — это просто отношение TPR к FPR. Теперь вам все понятно, в заключение…
Поверили?
Если серьезно, вы можете прочитать намного больше информации из диаграммы. Первый вопрос, который я хочу здесь обсудить: у нас же есть только один набор TPR, FPR, посчитанный на основе сделанных моделью предсказаний. Так откуда взялось такое количество точек для построения целого графика?
Все следует из того, как работает модель классификации. Когда вы строите классификационную модель, такую как дерево решений, и хотите определить, будут ли акции расти в цене или падать на основе входных данных. Модель сначала рассчитает вероятность увеличения или уменьшения, используя предоставленные вами исторические данные. После этого, основываясь на пороговом значении, она решит, будет ли результат увеличиваться или уменьшаться.
Да, ключевое слово здесь — порог. Разные пороговые значения создают разные TPR и FPR. Они представляют те самые точки, что образуют кривую ROC. Вы можете выбрать «Увеличение» в качестве предсказания модели, если полученная на основе исторических данных вероятность роста акций больше 50%. Также можете изменить пороговое значение и отобразить «Увеличение», только если соответствующая вероятность больше 90%. Если вы установите 90% порог вместо 50%, вы будете более уверены в том, что выбранные для «Увеличения» акции действительно вырастут. Но так вы можете упустить некоторые потенциально выгодные варианты.
Что значит синяя пунктирная линия на графике?
Как мы знаем, чем больше площадь под кривой (AUC), тем лучше классификация. Идеальная или наилучшая кривая — это вертикальная линия от (0,0) до (0,1), которая тянется до (1,1). Это означает: модель всегда может различить положительные и отрицательные случаи. Однако, если вы выбираете класс случайным образом для каждого семпла, TPR и FPR должны увеличиваться с одинаковой скоростью. Синяя пунктирная линия показывает кривую TPR и FPR при случайном определении positive или negative для каждого случая. Для этой диагональной линии площадь под кривой (AUC) составляет 0.5.
Что произойдет с TPR, FPR и ROC-кривой, если изменить пороговое значение?
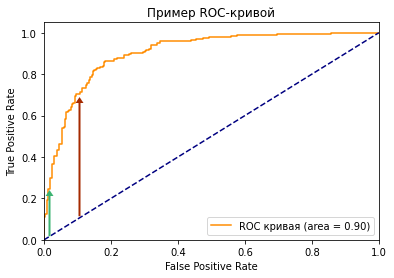
Посмотрите на две точки на ROC-кривой. Зеленая точка имеет очень высокий порог, это означает, что только если вы уверены на 99%, можете классифицировать случай как positive. Красная точка имеет относительно более низкий порог. Это означает, что вы можете классифицировать случай как positive, если вы уверены на 90%.
Как изменяются TPR и FPR при движении от зеленой точки к красной?
И TPR, и FPR увеличиваются. Когда вы уменьшаете порог, модель будет определять больше положительных случаев. Таким образом, TP увеличивается, как и TP/(TP + FN). С другой стороны, вы неизбежно ошибочно классифицируете некоторые отрицательные случаи как положительные из-за снижения порога, и поэтому FP и FP/(FP + TN) также увеличиваются.
Мы видим, что TPR и FPR положительно коррелируют. Вам нужно балансировать между максимальным охватом positive случаев и минимизацией неправильной классификации negative случаев.
Как выбрать оптимальную точку на кривой ROC?
Трудно определить оптимальную точку, потому что нужно выбрать наиболее подходящее пороговое значение, учитывая сферу применения модели. Однако общее правило — максимизировать разницу (TPR-FPR), которая на графике представлена вертикальным расстоянием между оранжевой и синей пунктирной линией.
Почему площадь под кривой ROC – хорошая метрика для оценки модели классификации?
Хорошая метрика модели машинного обучения должна отображать истинную и постоянную способность модели к прогнозированию. Это означает, что, если я изменю тестовый набор данных, он не должен давать другой результат.
ROC-кривая учитывает не только результаты классификации, но и вероятность предсказания всех классов. Например, если результат корректно классифицирован на основе 51% вероятности, то он, скорее всего, будет классифицирован неверно, если вы воспользуетесь другим тестовым датасетом. Кроме того, ROC-кривая также учитывает эффективность модели при различных пороговых значениях. Она является комплексной метрикой для оценки того, насколько хорошо разделяются случаи в разных группах.
Какое значение AUC является приемлемым для модели классификации?
Как я показал ранее, для задачи двоичной классификации при определении классов случайным образом, вы можете получить 0.5 AUC. Следовательно, если вы решаете задачу бинарной классификации, разумное значение AUC должно быть > 0.5. У хорошей модели классификации показатель AUC > 0.9, но это значение сильно зависит от сферы ее применения.
Как рассчитать AUC и построить ROC-кривую в Python?
Если вы просто хотите рассчитать AUC, вы можете воспользоваться пакетом metrics библиотеки sklearn (ссылка).
Если вы хотите построить ROC-кривую для результатов вашей модели, вам стоит перейти сюда.
Вот код для построения графика ROC, который я использовал в этой статье.
Логистическая регрессия и ROC-анализ — математический аппарат
Математический аппарат и назначение бинарной логистической регрессии — популярного инструмента для решения задач регрессии и классификации. ROC-анализ тесно связан с бинарной логистической регрессией и применяется для оценки качества моделей: позволяет выбрать аналитику модель с наилучшей прогностической силой, проанализировать чувствительность и специфичность моделей, подобрать порог отсечения.
Введение
Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований.
Логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC-анализ почти всегда можно увидеть в наборе Data Mining алгоритмов.
Логистическая регрессия
Логистическая регрессия — это разновидность множественной регрессии, общее назначение которой состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в случае, когда зависимая переменная является бинарной (т.е. может принимать только два значения). С помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).
Все регрессионные модели могут быть записаны в виде формулы:
y = F (x_1,\, x_2, \,\dots, \, x_n)
В множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:
Можно ли ее использовать для задачи оценки вероятности исхода события? Да, можно, вычислив стандартные коэффициенты регрессии. Например, если рассматривается исход по займу, задается переменная y со значениями 1 и 0, где 1 означает, что соответствующий заемщик расплатился по кредиту, а 0, что имел место дефолт.
Для решения проблемы задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной, мы предсказываем непрерывную переменную со значениями на отрезке [0,1] при любых значениях независимых переменных. Это достигается применением следующего регрессионного уравнения (логит-преобразование):
где P — вероятность того, что произойдет интересующее событие e — основание натуральных логарифмов 2,71…; y — стандартное уравнение регрессии.
Рис. 1 — Логистическая кривая
P’ = \log_e \Bigl(\frac
<1-P>\Bigr)
Это преобразование обычно называют логистическим или логит-преобразованием. Теоретически P’ может принимать любое значение. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), то эти преобразованные значения можно использовать в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии.
Существует несколько способов нахождения коэффициентов логистической регрессии. На практике часто используют метод максимального правдоподобия. Он применяется в статистике для получения оценок параметров генеральной совокупности по данным выборки. Основу метода составляет функция правдоподобия (likehood function), выражающая плотность вероятности (вероятность) совместного появления результатов выборки
L\,(Y_1,\,Y_2,\,\dots,\,Y_k;\,\theta) = p\,(Y_1;\, \theta)\cdot\dots\cdotp\,p\,(Y_k;\,\theta)
L\,*\,(Y;\,\theta) = \ln\,(L\,(Y;\,\theta)\,) \rightarrow \max
Логарифмическая функция правдоподобия равна:
Можно показать, что градиент g и гессиан H функции правдоподобия равны:
g = \sum_i (Y_i\,-\,P_i)\,X_i
H=-\sum_i P_i\,(1\,-\,P_i)\,X_i^T\,X_i\,\leq 0
Гессиан всюду отрицательно определенный, поэтому логарифмическая функция правдоподобия всюду вогнута. Для поиска максимума можно использовать метод Ньютона, который здесь будет всегда сходиться (выполнено условие сходимости метода):
Логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой есть коэффициенты логистической регрессии, а вес поляризации — константа регрессионного уравнения (рис. 2).
Рис. 2 — Представление логистической регрессии в виде нейронной сети
Однослойная нейронная сеть может успешно решить лишь задачу линейной сепарации. Поэтому возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. Однако для оценки качества модели логистической регрессии существует эффективный инструмент ROC-анализа, что является несомненным ее преимуществом.
Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.
ROC-анализ
ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.
В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.
В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.
Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.
| Модель | Фактически положительно | Фактически отрицательно |
|---|---|---|
| Положительно | TP | FP |
| Отрицательно | FN | TN |
Что является положительным событием, а что — отрицательным, зависит от конкретной задачи. Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным — «Здоровый пациент». И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.
При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates), выраженными в процентах:
Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.
Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев:
Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:
Заметим, что FPR=100-Sp
Попытаемся разобраться в этих определениях.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины — задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
ROC-кривая получается следующим образом:
Канонический алгоритм построения ROC-кривой
В результате вырисовывается некоторая кривая (рис. 3).
Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.
При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.
Рис. 4 — Сравнение ROC-кривых
Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0,5 («бесполезный» классификатор) до 1,0 («идеальная» модель).
Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5). Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций:
AUC = \int f(x)\,dx = \sum_i \Bigl[ \frac
Рис. 5 — Площадь под ROC-кривой
| Интервал AUC | Качество модели |
|---|---|
| 0,9-1,0 | Отличное |
| 0,8-0,9 | Очень хорошее |
| 0,7-0,8 | Хорошее |
| 0,6-0,7 | Среднее |
| 0,5-0,6 | Неудовлетворительное |
Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:
Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность или специфичность модели (рис. 6).
Рис. 6 — «Точка баланса» между чувствительностью и специфичностью
Существуют и другие подходы, когда ошибкам I и II рода назначается вес, который интерпретируется как цена ошибок. Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.
Как понять ROC-кривые с помощью Python
Если вы погуглите ROC curve machine learning, то Википедия выдаст вам такой ответ: Кривая рабочих характеристик приёмника, или ROC-кривая, представляет собой график функции, который иллюстрирует диагностические возможности системы двоичного классификатора при изменении её порога распознавания.
Ещё одно частое описание ROC-кривой: ROC-кривая отражает чувствительность модели к разным порогам классификации. Новичков эти определения могут сбить с толку. Попробуем разобраться и развить представление о ROC-кривых.
Что за чертовщина эта ROC-кривая?
Вариант, как понять ROC-кривую: она описывает взаимосвязь между чувствительностью модели (TPR, или true positives rate — доля истинно положительных примеров) и её специфичностью (описываемой в отношении долей ложноположительных результатов: 1-FPR).
Давайте разовьём эту концепцию. TPR, или чувствительность модели, является соотношением корректных классификаций положительного класса, разделённых на все положительные классы, доступные из набора данных:
FPR — доля ложноположительных примеров, false positives rate. Это соотношение между ложными срабатываниями (количество прогнозов, ошибочно отнесённых в положительные), и всеми доступными отрицательными классами. Математически:
Обобщая: вы сравниваете, как чувствительность модели меняется по отношению к ложно положительным долям на разных порогах отсечения. Модель опирается на порог отсечения, чтобы принимать решения по входным данным и относить их к положительным.
Разделение проблемы с порогами отсечения
Поначалу интуиция толкала к пониманию роли порогов отсечения. Мне помогла мысленная картина:

С такой классической визуализацией до меня дошло первое представление, а именно: идеальная модель — та, в которой доля истинно положительных результатов максимально высока, в то же время доля ложно положительных результатов удерживается как можно ниже.
Порог соответствует переменной T (например, значение между 0 и 1), служит границей принятия решения для классификатора и влияет на компромисс между TPR и FPR. Давайте напишем код, чтобы визуализировать все компоненты.
Визуализация ROC-кривой
Сгенерировать данные с помощью drawdata для Jupyter
Импортировать сгенерированные данные в фреймворк pandas
Подобрать модель логистической регрессии к данным
Получить прогнозы модели логистической регрессии в виде значений вероятности
Установить другие пороги отсечения
Сделать окончательные выводы
Импортируем зависимости
Сгенерируем данные с помощью пакета drawdata для блокнотов Jupyter
Что получается на выходе:
Импортируем данные в фреймворк pandas
Подберём модель логистической регрессии к данным
Получим прогнозы модели логистической регрессии в виде значений вероятности
Установим другие пороговые значения
Визуализируем ROC-кривую
Сделаем окончательные выводы
Изменяя порог, мы получили возрастающие значения как истинно положительных, так и ложно положительных долей. В хорошей модели порог отсечения ставит истинно положительные доли как можно ближе к 1, при этом сохраняя ложно положительные доли на самом нижнем из возможных уровней.
Как нам выбрать лучший порог?
Простой способ: выбрать тот порог, у которого максимальная сумма из истинно положительных и ложно отрицательных долей (1-FPR).
Другой критерий: простой выбор точки, ближайшей к левому верхнему углу ROC-кривой. Однако такой критерий подразумевает, что истинно положительный и истинно отрицательный показатели имеют одинаковый вес. В некоторых случаях, такая выборка не подходит, поскольку отрицательное влияние ложно положительных долей весомее, чем влияние истинно положительных.
Итоговые выводы о ROC-кривой
Я считаю, что в долгосрочной перспективе машинного обучения полезно потратить время на освоение оценочных показателей. В этой статье вы узнали:
Базовое представление о том, как работают ROC-кривые
Как пороги отсечения влияют на соотношение чувствительности и особенности модели
Как использовать ROC-кривые для выбора оптимальных порогов отсечения
Кривая ошибок
Материал из MachineLearning.
Содержание
Кривая ошибок или ROC-кривая – графичекая характеристика качества бинарного классификатора, зависимость доли верных положительных классификаций от доли ложных положительных классификаций при варьировании порога решающего правила. Преимуществом ROC-кривой является её инвариантность относительно отношения цены ошибки I и II рода.
Задача классификации
Для байесовского классификатора при достаточно общих предположениях доказано, что оптимальное значение порога зависит только от соотношения цены ошибок:
Заметим, что частным случаем линейного байесовского классификатора является логистическая регрессия.
TPR и FPR
ROC-кривая
ROC-кривая монотонно не убывает. Чем выше лежит кривая, тем лучше качество классификации.
На рисунке 1 приведена ROC-кривая, соответствующая худшему случаю — алгоритму «случайного гадания». На рисунке 2 изображён общий случай. Лучший случай — это кривая, проходящая через точки
ROC-кривая может быть вычислена по любой выборке. Однако ROC-кривая, вычисленная по обучающей выборке, является оптимистично смещённой влево-вверх вследствие переобучения. Величину этого смещения предсказать довольно трудно, поэтому на практике ROC-кривую всегда оценивают по независомой тестовой выборке.
Площадь под ROC-кривой AUC
Площадь под ROC-кривой AUC (Area Under Curve) является агрегированной характеристикой качества классификации, не зависящей от соотношения цен ошибок. Чем больше значение AUC, тем «лучше» модель классификации. Данный показатель часто используется для сравнительного анализа нескольких моделей классификации.
Алгоритм построения ROC-кривой
Следующий алгоритм строит ROC-кривую за обращений к дискриминантной функции.
Чувствительность и специфичность
Наряду с FPR и TPR используют также показатели чувствительности и специфичности, которые также изменяются в интервале :
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицинской диагностики, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
История
Термин операционная характеристика приёмника (Receiver Operating Characteristic, ROC) пришёл из теории обработки сигналов. Эту характеристику впервые ввели во время II мировой войны, после поражения американского военного флота в Пёрл Харборе в 1941 году, когда была осознана проблема повышения точности распознавания самолётов противника по радиолокационному сигналу. Позже нашлись и другие применения: медицинская диагностика, приёмочный контроль качества, кредитный скоринг, предсказание лояльности клиентов, и т.д.