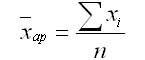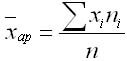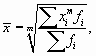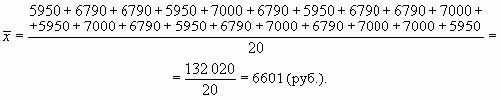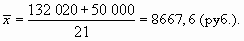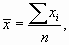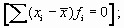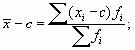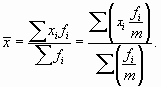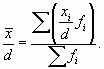что показывает средняя арифметическая величина
Средняя арифметическая, её виды
Понятие средней арифметической
Средняя арифметическая — такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий объем импорта за год — это сумма импорта, деленная на 12 месяцев.
Средняя арифметическая может быть вычислена по формуле:
где n — численность совокупности (или число месяцев).
Например, суммарный объем импорта в 2013 году составил 314967 млн. долл. Для нахождения этой величины мы просуммировали данные по месяцам
| Месяц | Импорт |
| Январь | 19806,1 |
| Февраль | 24632,8 |
| Март | 26608,7 |
| Апрель | 28195,9 |
| Май | 24326,4 |
| Июнь | 26097,8 |
| Июль | 28023,7 |
| Август | 25987,2 |
| Сентябрь | 26263,1 |
| Октябрь | 28098,4 |
| Ноябрь | 27193,3 |
| Декабрь | 29733,7 |
| Сумма | 314967,0 |
Средняя арифметическая находится так: 314967 : 12 = 26247,3 млн. долл. (12 — число месяцев)
Смотрите видео по нахождению средней арифметической величины
Виды средней арифметической величины
Средняя арифметическая величина используется в форме простой средней и взвешенной средней. Средняя арифметическая простая равна простой сумме отдельно взятых значений осредняемого признака, разделенная на общее число этих значений. В различных контрольных по статистике она используется тогда, когда имеются несгруппированные индивидуальные значения признака, и может быть вычислена по формуле:
где n — общая численность совокупности значений х.
Средняя арифметическая взвешенная — это средняя из вариантов, которые повторяются разное число раз или имеют различный вес. Она может быть рассчитана по формуле:
Основные свойства средней арифметической
Часто приходится вычислять среднюю по групповым средним или по средним отдельных частей совокупности. Например, средняя рождаемость в стране представляет собой среднее из средних рождаемости по отдельным регионам страны. Средние из средних определяются так же, как и средние из первоначальных значений признака.
Средние величины в статистике
Начиная рассуждать о средних величинах, чаще всего вспоминают, как заканчивали школу и поступали в учебное заведение. Тогда по аттестату рассчитывался средний балл: все оценки (и хорошие, и не очень) складывали, полученную сумму делили на их количество. Так вычисляется самый простой вид средней, которая называется средняя арифметическая простая. На практике в статистике применяются различные виды средних величин: арифметическая, гармоническая, геометрическая, квадратическая, структурные средние. Тот или иной их вид используется в зависимости от характера данных и целей исследования.
Средняя величина является наиболее распространенным статистическим показателем, с помощью которого дается обобщающая характеристика совокупности однотипных явлений по одному из варьирующих признаков. Она показывает уровень признака в расчете на единицу совокупности. С помощью средних величин проводится сравнение различных совокупностей по варьирующим признакам, изучаются закономерности развития явлений и процессов общественной жизни.
В статистике применяются два класса средних: степенные (аналитические) и структурные. Последние используются для характеристики структуры вариационного ряда и будут рассмотрены далее в гл. 8.
К группе степенных средних относят среднюю арифметическую, гармоническую, геометрическую, квадратическую. Индивидуальные формулы для их вычисления можно привести к виду, общему для всех степенных средних, а именно
Главным условием, при котором можно использовать степенные средние в статистическом анализе, является однородность совокупности, которая не должна содержать исходных данных, резко различающихся по своему количественному значению (в литературе они носят название аномальных наблюдений).
Продемонстрируем важность этого условия на следующем примере.
Пример 6.1. Вычислим среднюю заработную плату сотрудников малого предприятия.
| № п/п | Заработная плата, руб. | № п/п | Заработная плата, руб. |
|---|---|---|---|
| 1 | 5 950 | 11 | 7 000 |
| 2 | 6 790 | 12 | 5 950 |
| 3 | 6 790 | 13 | 6 790 |
| 4 | 5 950 | 14 | 5 950 |
| 5 | 7 000 | 5 | 6 790 |
| 6 | 6 790 | 16 | 7 000 |
| 7 | 5 950 | 17 | 6 790 |
| 8 | 7 000 | 18 | 7 000 |
| 9 | 6 790 | 19 | 7 000 |
| 10 | 6 790 | 20 | 5 950 |
Для расчета среднего размера заработной платы необходимо просуммировать заработную плату, начисленную всем работникам предприятия (т.е. найти фонд заработной платы), и разделить на число работающих:
А теперь добавим в нашу совокупность всего лишь одного человека (директора этого предприятия), но с окладом в 50 000 руб. В таком случае вычисляемая средняя будет совсем другая:
Как видим, она превышает 7000 руб., т.д. она больше всех значений признака за исключением одного-единственного наблюдения.
Для того чтобы таких случаев не происходило на практике, и средняя не теряла бы своего смысла (в примере 6.1 она уже не выполняет роль обобщающей характеристики совокупности, которой должна быть), при расчете средней следует аномальные, резко выделяющиеся наблюдения либо исключить из анализа и тем самым сделать совокупность однородной, либо разбить совокупность на однородные группы и вычислить средние значения по каждой группе и анализировать не общую среднюю, а групповые средние значения.
6.1. Средняя арифметическая и ее свойства
Средняя арифметическая вычисляется либо как простая, либо как взвешенная величина.
При расчете средней заработной платы по данным таблицы примера 6.1 мы сложили все значения признака и поделили на их количество. Ход наших вычислений запишем в виде формулы средней арифметической простой
Пример 6.2. Теперь сгруппируем наши данные из таблицы примера 6.1, т.д. построим дискретный вариационный ряд распределения работающих по уровню заработной платы. Результаты группировки представлены в таблице.
| Заработная плата, руб. | Численность работников |
|---|---|
| 5 950 | 6 |
| 6 790 | 8 |
| 7 000 | 6 |
| Итого | 20 |
Запишем выражение для вычисления среднего уровня заработной платы в более компактной форме:
В примере 6.2 была применена формула средней арифметической взвешенной
Расчет средней арифметической взвешенной удобно проводить в таблице, как это показано ниже (табл. 6.3):
| Исходные данные | Расчетный показатель | |
| заработная плата, руб. | численность работающих, чел. | фонд заработной платы, руб. |
| xi | fi | xifi |
| 5 950 | 6 | 35 760 |
| 6 790 | 8 | 54 320 |
| 7 000 | 6 | 42 000 |
| Итого | 20 | 132 080 |
Следует отметить, что средняя арифметическая простая используется в тех случаях, когда данные не сгруппированы или сгруппированы, но все частоты равны между собой.
Пример 6.3. По результатам выборочного обследования одной из групп населения рассчитаем размер среднедушевого денежного дохода.
| Среднедушевой денежный доход, руб. в месяц | Численность населения к итогу, % fi | Середины интервалов xi | xifi |
|---|---|---|---|
| До 1 000 | 4,1 | 500 | 2 050 |
| 1 000-2 000 | 8,6 | 1 500 | 12 900 |
| 2 000-4 000 | 12,9 | 3 000 | 38 700 |
| 4 000-6 000 | 13,0 | 5 000 | 65 000 |
| 6 000-8 000 | 10,5 | 7 000 | 73 500 |
| 8 000-10 000 | 27,8 | 9 000 | 250 200 |
| 10 000-20 000 | 12,7 | 15 000 | 190 500 |
| 20 000 и выше | 10,4 | 25 000 | 260 000 |
| Итого | 100,0 | — | 892 850 |
Тогда среднедушевой размер месячного дохода составит
Средняя арифметическая величина обладает рядом математических свойств. Приведем основные из них:
где 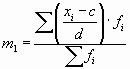
Пример 6.4. Рассчитаем среднюю прибыль по группе банков способом моментов.