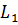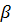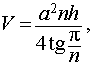что представляет осевое сечение цилиндра

Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей

Геометрическая фигура

Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.

Вам будет интересно: Предположение — это и высказанная вслух мысль, и основа прогресса

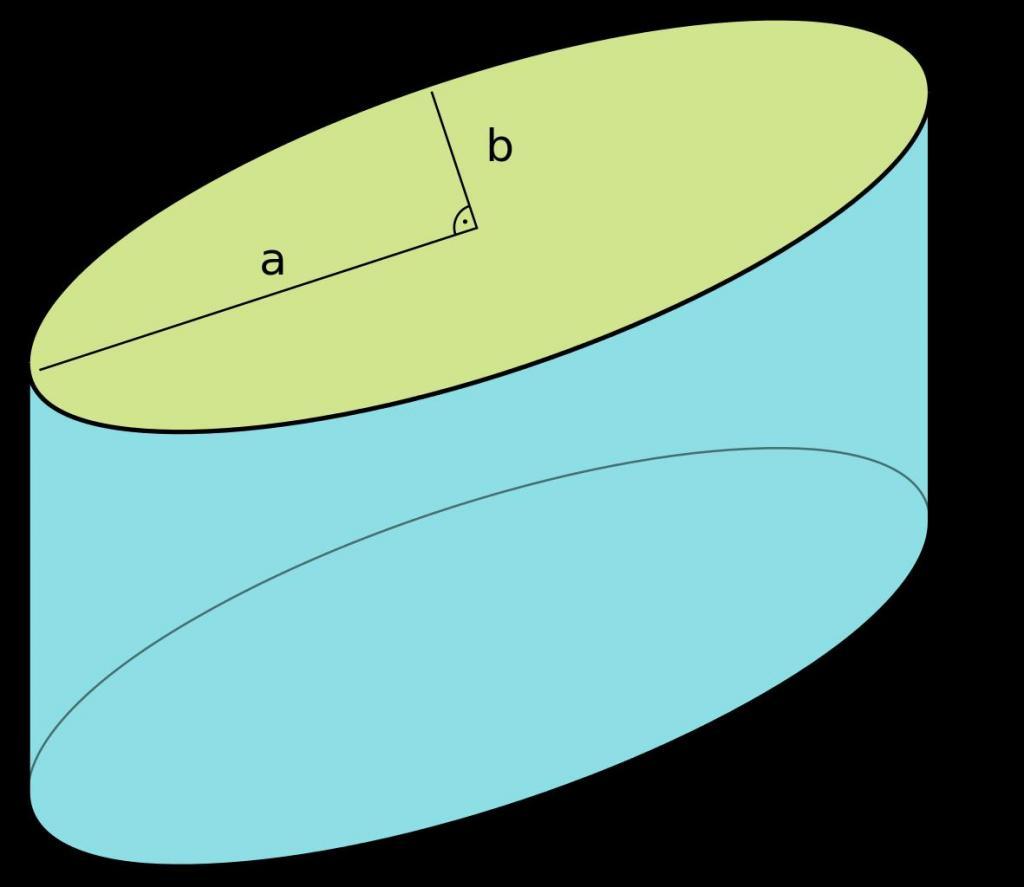
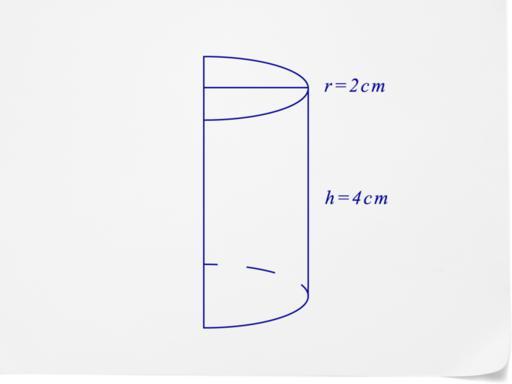
На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.

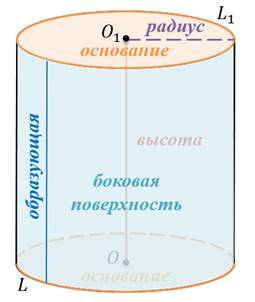
Здесь отрезок длиной h является его образующей и высотой.

Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.

Прямой и наклонный цилиндры

Перед тем как переходить к рассмотрению осевого сечения цилиндров, расскажем, какие типы этих фигур бывают.

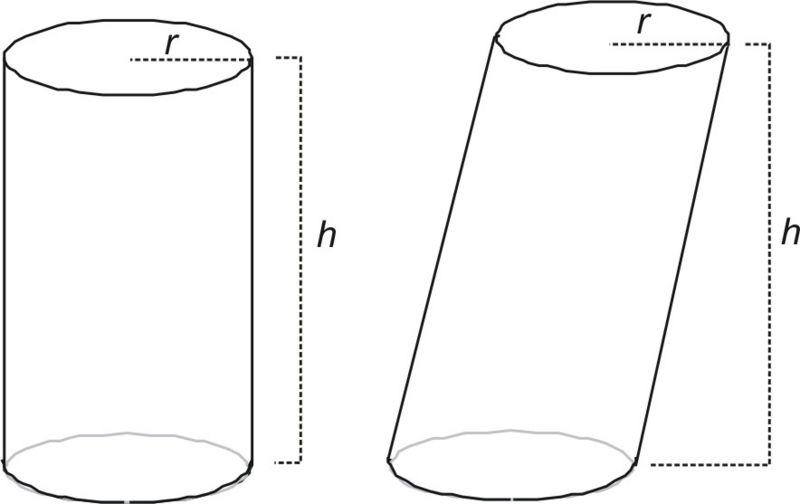
Если образующая линия перпендикулярна основаниям фигуры, тогда говорят о прямом цилиндре. В противном случае цилиндр будет наклонным. Если соединить центральные точки двух оснований, то полученная прямая называется осью фигуры. Приведенный рисунок демонстрирует разницу между прямым и наклонным цилиндрами.

Видно, что для прямой фигуры длина образующего отрезка совпадает со значением высоты h. Для наклонного цилиндра высота, то есть расстояние между основаниями, всегда меньше длины образующей линии.

Далее охарактеризуем осевые сечения обоих типов цилиндров. При этом будем рассматривать фигуры, основаниями которых является круг.

Осевое сечение прямого цилиндра

Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.

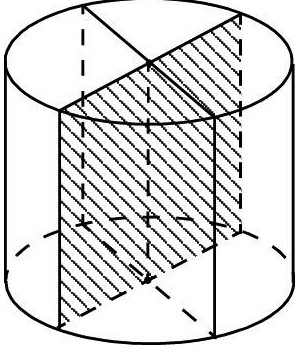
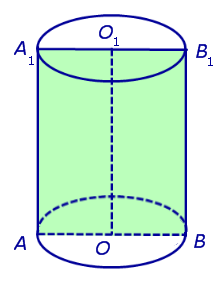
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.

Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.

Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:

Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.

Осевое сечение наклонного цилиндра

Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:

Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:

l2 = √(d2 + b2 + 2*b*d*cos(α))

Задача с прямым цилиндром

Для вычисления искомой площади необходимо найти либо радиус, либо диаметр основания цилиндра. Для этого воспользуемся формулой для общей площади Sf фигуры:

Поскольку сечение осевое представляет собой квадрат, то это означает, что радиус r основания в два раза меньше высоты h. Учитывая это, можно переписать равенство выше в виде:

Sf = 2*pi*r*(r + 2*r) = 6*pi*r2

Теперь можно выразить радиус r, имеем:

Поскольку сторона квадратного сечения равна диаметру основания фигуры, то для вычисления его площади S будет справедлива следующая формула:

S = (2*r)2 = 4*r2 = 2*Sf / (3*pi)

Мы видим, что искомая площадь однозначно определяется площадью поверхности цилиндра. Подставляя данные в равенство, приходим к ответу: S = 21,23 см2.

Источник

Сечение цилиндра: определение, виды, его образующая

Кратко о цилиндре

Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.

Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.

Осевое сечение

Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как найти площадь сечения

Формула 1

\(S = d*h,\)

где \(d\) — диаметр, а \(h\) — высота всей фигуры.

Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).

Формула 2

\(S = a*h, \)

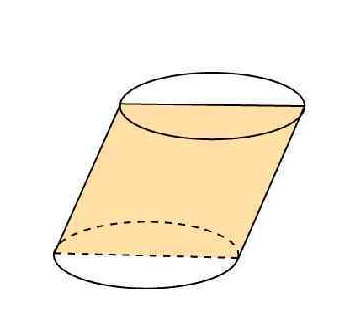
Осевое сечение наклонного цилиндра

Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.

Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:

Примеры задач

Рассмотрим пару задач на осевое сечение с решениями.

Задача 1

Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?

Решение

Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:

Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:

\(Sц = 2pi * r * (r + 2r) = 6 * pi * r²\)

Исходя из этого, будем выражать радиус:

Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:

\(S = (2*r)2 = 4*r2 = 2*Sц/ (3*pi)\)

Задача 2

Решение

Так как площадь сечения — прямоугольник, то \(Sc = AB * BC = h * 2r.\) Тогда \(h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).\)

Источник

Цилиндры

Основные определения и свойства цилиндра

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Сечения цилиндра

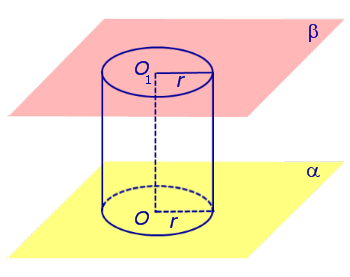
Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
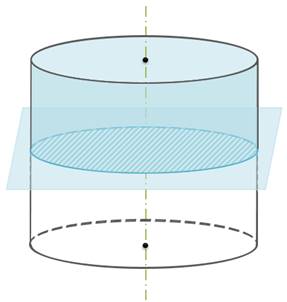
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

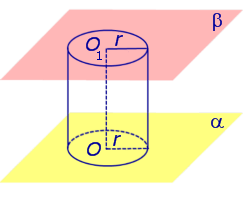
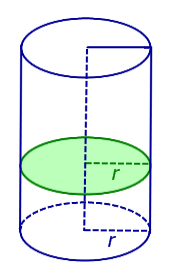
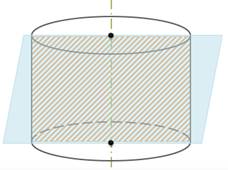
Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра

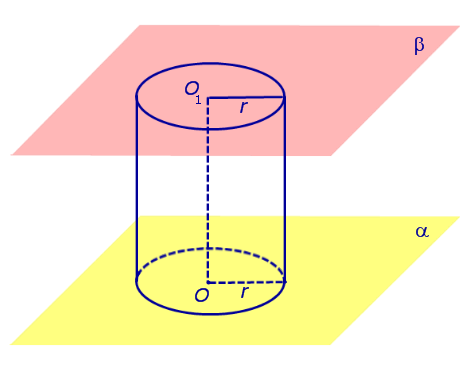
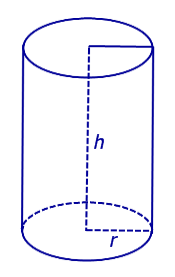
Для цилиндра с радиусом r и высотой h (рис. 5)

введем следующие обозначения

Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

Источник

Понятие цилиндра

Урок 12. Геометрия 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Понятие цилиндра»

На этом уроке мы вспомним понятие цилиндра. Дадим его определение. Рассмотрим, какими элементами обладает цилиндр.

Вокруг нас существует множество объектов, которые являются физическими моделями цилиндра, или проще говоря, имеют форму цилиндра.

Например, кружки и стаканы имеют форму цилиндра. Карандаши, шляпы, пуфики, барабан также имеют форму цилиндра.

Некоторые архитектурные сооружения.

Колонны храмов и соборов, выполненные в форме цилиндра, подчеркивают их гармонию и красоту.

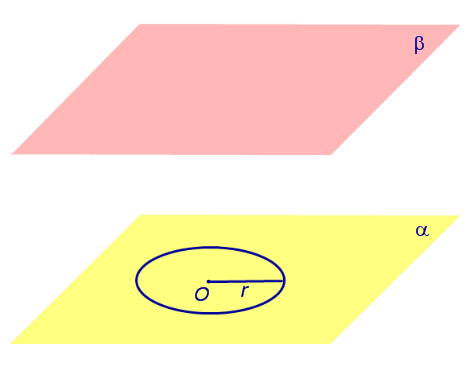
Итак, перейдём к самому цилиндру. Рассмотрим произвольную плоскость и окружность с центром О радиуса , лежащую в этой плоскости. Через каждую точку окружности проведем прямую, перпендикулярную к плоскости .

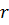
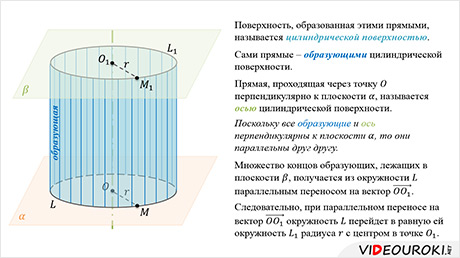
Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые – образующими цилиндрической поверхности.

Прямая, проходящая через точку О перпендикулярно к плоскости , называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости , то они параллельны друг другу.

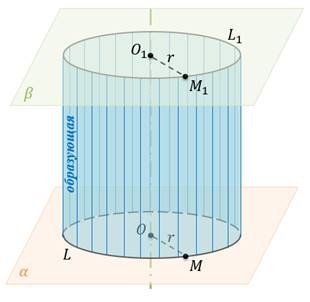
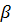
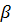
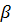
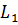
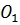
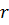
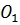
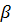
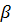
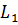
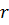
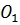
Рассмотрим теперь плоскость , параллельную плоскости . Отрезки образующих, заключённые между плоскостями и , параллельны и равны друг другу. По построению концы этих отрезков, расположенные в плоскости , заполняют окружность . Концы же, расположенные в плоскости , заполняют окружность с центром радиуса , где – точка пересечения плоскости с осью цилиндрической поверхности. Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости , получается из окружности параллельным переносом на вектор . Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор . окружность перейдёт в равную ей окружность радиуса с центром в точке .

Тело, ограниченное цилиндрической поверхностью и двумя равными кругами с границами и , называется цилиндром.

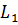
Можно ещё услышать и такое определение: прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями и , которые перпендикулярны образующим цилиндрической поверхности.

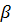
Назовём элементы цилиндра.

Круги называются основаниями цилиндра.

А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.

Ось цилиндрической поверхности называется осью цилиндра.

Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между основаниями цилиндра.

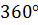
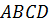
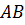
Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон на . Итак, если взять некоторый прямоугольник и вращать его вокруг одной из сторон, например, вокруг стороны , то в результате получим тело, которое и называется цилиндром.

В этом случае основания цилиндра образуются вращением сторон 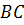и , а боковая поверхность цилиндра образуется вращении стороны .

Теперь рассмотрим сечения цилиндра различными плоскостями.

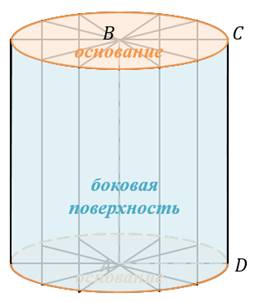
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.

Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось.

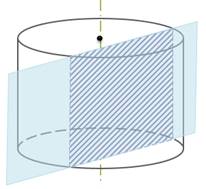
Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие цилиндра, а две другие – хорды оснований цилиндра.

Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.

В самом деле, такая секущая плоскость отсекает от данного цилиндра тело, которое также является цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.

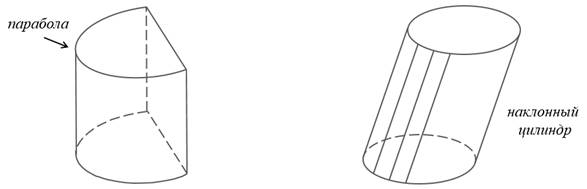
Замечание. На практике очень часто встречаются предметы, которые имеют форму сложных цилиндров.

На экране, на первом рисунке вы видите цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком. На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований, такой цилиндр называют еще наклонным цилиндром. Однако в дальнейшем мы будем рассматривать только прямые круговые цилиндры.

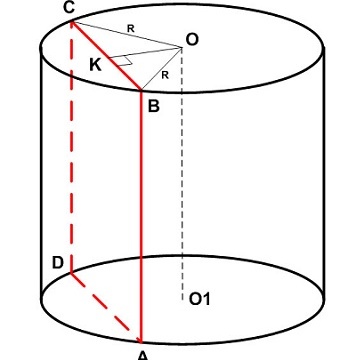
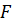
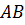
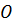
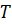
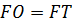
Задача: точка – середина образующей цилиндра, центрами оснований которого являются точки и . Верно ли, что ?

Решение: рассмотрим и .

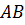
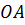
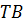
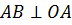
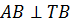
Образующая перпендикулярна плоскостям, в которых лежат основания цилиндра. Следовательно, она перпендикулярна любой прямой лежащей в этих плоскостях. Прямые и являются радиусами цилиндра и лежат в плоскостях оснований. Значит, прямая и . Отсюда получаем, что и – прямоугольные.

Так как основаниями цилиндра являются равные круги, то 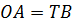, как радиусы.

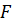
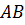
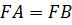
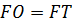
Так как по условию задачи точка – середина образующей цилиндра, то отрезки . Значит, равны по двум катетам. Отсюда вытекает, что .

Ответ: .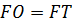

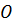
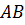
Задача: точка – центр основания цилиндра. Отрезок – диаметр другого его основания. Вычислите площадь , если радиус цилиндра равен см, а его высота – см.

Решение: напомним, что площадь треугольника находится по формуле . Заметим, что высота цилиндра является и высотой нашего и равна . А основание треугольника есть диаметр цилиндра и равно оно двум радиусам, т.е. (см).

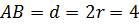
Подставим в формулу площади треугольника высоту и длину основания треугольника. Посчитаем. Получим, что площадь треугольника равна 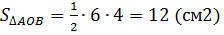. Не забудем записать ответ.

Задача: радиус цилиндра 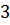см, а его высота – см. Вычислите площадь осевого сечения.

Решение: напомним, что осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Высота цилиндра – это есть длина образующей 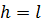. Следовательно, ширина осевого сечения равна . Длина сечения равна диаметру основания цилиндра. И значит, равна (см).

Теперь вычислим площадь осевого сечения. Она равна ().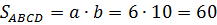

На этом уроке мы вспомнили понятие цилиндра. Узнали, что тело, ограниченное цилиндрической поверхностью и двумя кругами с границами и , называется цилиндром. Или прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями и , которые перпендикулярны образующим цилиндрической поверхности. Назвали элементы цилиндра. А также рассмотрели сечения цилиндра различными плоскостями.

Источник