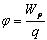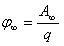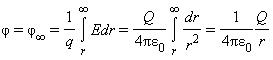что представляют собой эквипотенциальные поверхности поля для точечного заряда
Как сказал.
В мире нет ничего особенного. Никакого волшебства. Только физика.
Чак Паланик
Вопросы к экзамену
Для всех групп технического профиля

Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Урок 25-2. (дополнительный материал) Эквипотенциальные поверхности
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Во многих задачах электростатики при вычислении потенциалов за начальную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям.
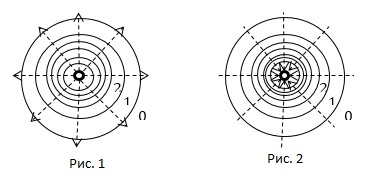
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рисунке представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
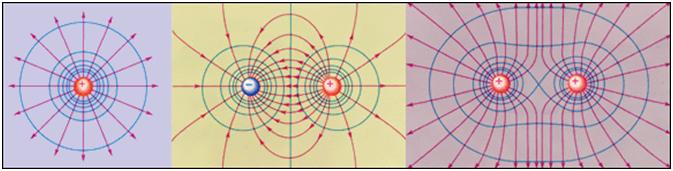
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Свойства эквипотенциальных поверхностей:
Эквипотенциальные поверхности — справочник студента
Возьмем производную точку М и обозначим работу по перемещению пробного заряда qпр от М к А через φ(А), а от М к В через φ(В). После чего будет осуществлено перемещение данного заряда от А к В по пути А- М – В.
Так как работу перехода М – А мы обозначили как φ(А), то обратный переход А – М также будет φ(А), из чего следует формула:
Положение точки М по сути безразлично, так как в данном случае играет роль только разность значений функций φ. Однако, задав координаты точки М мы однозначно определим величины функций φ(А) и φ(В), хотя на величину разности φ(А) — φ(В) положение точки М никак не влияет. Как только координаты точки М выбраны, число φ определяется в любой точке пространства.
Отсюда следует важный вывод – величина φ является функцией координат x, y, z и скаляром электростатического поля. Данная скалярная функция φ называется потенциалом электростатического поля. Точка отсчета М для удобства расчетов помещается в бесконечность. Потенциал бесконечно удаленной точки принимают равным нулю φ = 0.
Физическая величина, которая равна отношению потенциальной энергии, приобретаемой положительным зарядом qпр, при его переносе из бесконечности в данную точку пространства к этому заряду, то есть:
Потенциал – это энергетическая характеристика поля. Численно он равен работе, которую нужно совершить при перенесении единичного заряда из бесконечности, где потенциальная энергия считается равной нулю, в данную точку поля.
Совокупность точек с одинаковым потенциалом образуют эквипотенциальную поверхность или поверхность равного потенциала (φ = const). С помощью данных точек эквипотенциальную поверхность можно изобразить графически.
На рисунке ниже изображено электрическое поле равномерно заряженного диска, где пунктирные линии – эквипотенциальные поверхности, а сплошные – линии напряженности.
Данный рисунок иллюстрирует общее свойство эквипотенциальных поверхностей и силовых линий – эквипотенциальная поверхность и силовая линия, проведенная через любую точку, в данной точке взаимно перпендикулярны.
Поскольку все точки эквипотенциальной поверхности имеют одинаковый потенциал (φ1 – φ2 = 0), то работа не совершается при перемещении заряда вдоль нее.
Из этого следует, что действующий на заряд вектор силы, а значит и вектор напряженности все время перпендикулярен к перемещению.
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности — Класс!ная физика
«Физика — 10 класс»
Какие две характеристики электростатического поля вы уже знаете? Как они определяются? Для чего электрическое поле изображают силовыми линиями?
Каждой точке электрического поля соответствуют определённые значения потенциала и напряжённости. Найдём связь напряжённости электрического поля с разностью потенциалов.
Пусть заряд q перемещается в направлении вектора напряжённости однородного электрического поля Е из точки 1 в точку 2, находящуюся на расстоянии Δd от точки 1 (рис. 14.33). Электрическое поле совершает работу
Эту работу согласно формуле (14.19) можно выразить через разность потенциалов между точками 1 и 2:
Приравнивая выражения для работы, найдём модуль вектора напряжённости поля:
В этой формуле U — разность потенциалов между точками 1 и 2, лежащими на одной силовой линии поля (см. рис. 14.33).
Формула (14.21) показывает: чем меньше меняется потенциал на расстоянии Δd, тем меньше напряжённость электростатического поля. Если потенциал не меняется совсем, то напряжённость поля равна нулю.
Формула (14.21) справедлива для произвольного электростатического поля, если только расстояние Δd настолько мало, что изменением напряжённости поля на этом расстоянии можно пренебречь.
Сравним поле силы тяжести и однородное электростатическое поле.
Единица напряжённости электрического поля. Единицу напряжённости электрического поля в СИ устанавливают, используя формулу (14.21).
Эквипотенциальные поверхности.
При перемещении заряда под углом 90° к силовым линиям электрическое поле не совершает работу, так как электростатическая сила перпендикулярна перемещению.
Значит, если провести поверхность, перпендикулярную в каждой её точке силовым линиям, то при перемещении заряда вдоль этой поверхности работа не совершается.
А это означает, что все точки поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал.
Поверхности равного потенциала называют эквипотенциальными.
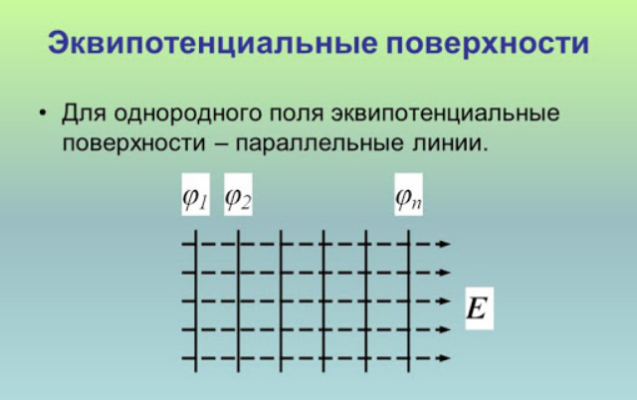
Эквипотенциальные поверхности однородного поля представляют собой плоскости (рис. 14.34, а), а поля точечного заряда — концентрические сферы (рис. 14.34, б).
Эквипотенциальные поверхности качественно характеризуют распределение поля в пространстве подобно тому, как линии уровня отражают рельеф поверхности на географических картах. Вектор напряжённости перпендикулярен эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.
Эквипотенциальные поверхности строятся обычно так, что разность потенциалов между двумя соседними поверхностями постоянна. Поэтому согласно формуле (14.21) расстояния между соседними эквипотенциальными поверхностями увеличиваются по мере удаления от точечного заряда, так как напряжённость поля уменьшается.
Эквипотенциальные поверхности однородного поля расположены на равных расстояниях друг от друга.
Эквипотенциальной является поверхность любого проводника в электростатическом поле. Ведь силовые линии перпендикулярны поверхности проводника. Причём не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряжённость поля внутри проводника равна нулю, значит, равна нулю и разность потенциалов между любыми точками проводника.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика — Электрический заряд и элементарные частицы. Закон сохранения заряд — Закон Кулона. Единица электрического заряда — Примеры решения задач по теме «Закон Кулона» — Близкодействие и действие на расстоянии — Электрическое поле — Напряжённость электрического поля. Силовые линии — Поле точечного заряда и заряженного шара.
Принцип суперпозиции полей — Примеры решения задач по теме «Напряжённость электрического поля.
Принцип суперпозиции полей» — Проводники в электростатическом поле — Диэлектрики в электростатическом поле — Потенциальная энергия заряженного тела в однородном электростатическом поле — Потенциал электростатического поля и разность потенциалов — Связь между напряжённостью электростатического поля и разностью потенциалов.
Эквипотенциальные поверхности — Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» — Электроёмкость. Единицы электроёмкости. Конденсатор — Энергия заряженного конденсатора. Применение конденсаторов — Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Эквипотенциальная поверхность (№1)
ВНИМАНИЕ! У этого текста есть несколько вариантов. Ссылки находятся после текста
Вокруг точечного заряженного тела существует бесконечно большое множество точек, в которых потенциалы будут одинаковы. Все они будут лежать на сферической поверхности радиуса r с центром в источнике поля. Такую поверхность называют эквипотенциальной.
Эквипотенциальная поверхность — это геометрическое место точек равных потенциалов.
Если силовые линии создают силовой «образ» поля, то эквипотенциальные поверхности позволяют средствами графики изобразить энергетическую структуру электрического поля.
Для поля точечного заряженного тела эквипотенциальные поверхности являются концентрическими сферами (рис. 4.56). Линии напряженности электрического поля, направленные вдоль радиусов этих сфер, перпендикулярны эквипотенциальным поверхностям. И это — общее правило при графическом изображении эквипотенциальных поверхностей.
Линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям.
 |
| Рис. 4.56. Эквипотенциальные поверхности заряженного поля |
 |
| Рис. 4.57. Эквипотенциальные поверхности однородного электростатического поля |
Эквипотенциальные поверхности однородного поля параллельных пластин параллельны этим пластинам (рис. 4.57). Да и сами заряженные пластины являются эквипотенциальными поверхностями.
Для более сложных полей эквипотенциальные поверхности имеют более сложную форму (рис. 4.58 и 4.59).
Линии напряженности поля показывают и направление уменьшения потенциала. Он уменьшается в направлении линий напряженности поля.
Отдельным примером эквипотенциальной поверхности является поверхность заряженного проводника. Доказательством этого является тот факт, что линии напряженности электростатического поля перпендикулярны эквипотенциальным поверхностям. Материал с сайта http://worldofschool.ru
 |
| Рис. 4.58. Эквипотенциальные поверхности неоднородного электростатического поля |
 |
| Рис. 4.59. Эквипотенциальные поверхности электростатического поля сложной структуры |
Эквипотенциальные поверхности — это не просто геометрические построения.
Они отображают тот факт, что при перемещении заряженного тела по эквипотенциальной поверхности работа равна нулю, поскольку потенциальная энергия тела при этом не изменяется.
Универсальным примером эквипотенциальной поверхности является поверхность проводника. Таким образом, заряженный проводник имеет определенный потенциал, одинаковый во всех точках его поверхности.
На этой странице материал по темам: Вопросы по этому материалу:
Эквипотенциальные линии
Задача обучения
Основные пункты
Термины
Эквипотенциальные линии отображают одномерные участки, где электрический потенциал остается неизменным.
То есть, для такого заряда (где бы он ни находился на эквипотенциальной линии) не нужно осуществлять работу, чтобы сдвинуться с одной точки на другую в пределах конкретной линии.
Линии эквипотенциальной поверхности бывают прямыми, изогнутыми или неправильными. Все это основывается на распределении зарядов. Они располагаются радиально вокруг заряженного тела, поэтому остаются перпендикулярными к линиям электрического поля.
Одиночный точечный заряд
Для одиночного точечного заряда формула потенциала:
Здесь наблюдается радиальная зависимость, то есть, независимо от дистанции к точечному заряду потенциал остается неизменным. Поэтому эквипотенциальные линии принимают круглую форму с точечным зарядом в центре.
Изолированный точечный заряд с линиями электрического поля (синий) и эквипотенциальными (зеленый)
Множественные заряды
Если контактирует несколько дискретных зарядов, то мы видим, как перекрываются их поля. Это перекрытие заставляет потенциал объединяться, а эквипотенциальные линии перекашиваться.
Если присутствует несколько зарядов, то эквипотенциальные линии формируются нерегулярно. В точке между зарядами контрольный способен ощущать эффекты от обоих зарядов
Непрерывный заряд
Если заряды расположены на двух проводящих пластинах в условиях статического баланса, где заряды не прерываются и находятся на прямой, то и эквипотенциальные линии выпрямляются. Дело в том, что непрерывность зарядов вызывает непрерывные действия в любой точке.
Если заряды вытягиваются в линию и лишены прерывания, то эквипотенциальные линии идут прямо перед ними. В качестве исключения можно вспомнить только изгиб возле краев проводящих пластин
Непрерывность нарушается ближе к концам пластин, из-за чего на этих участках создается кривизна – краевой эффект.
Читайте нас на Яндекс.Дзен
Линии поля; эквипотенциальные поверхности
Теперь мы собираемся дать геометрическое описание электростатического поля. Два закона электростатики: один — о пропорциональности потока и внутреннего заряда и другой — о том, что электрическое поле есть градиент потенциала, могут также быть изображены геометрически. Мы проиллюстрируем это двумя примерами.
Первый пример: возьмем поле точечного заряда. Проведем линии в направлении поля, которые повсюду касательны к векторам поля (фиг. 4.12). Их называют линиями поля. Линии поля всюду показывают направление электрического вектора. Но, кроме этого, мы хотим изобразить и абсолютную величину вектора.
Можно ввести такое правило: пусть напряженность электрического поля представляется «плотностью» линий. Под этим мы подразумеваем число линий на единицу площади, перпендикулярной линиям. С помощью этих двух правил мы можем начертить картину электрического поля.
Для точечного заряда плотность линий должна убывать как 1/r2.
Но площадь сферической поверхности, перпендикулярной к линиям на всех радиусах r, возрастает как r2, так что если мы сохраним всюду, на всех расстояниях от центра, одно и то же число линий, то их плотность останется пропорциональной величине поля.
Мы можем гарантировать неизменность числа линий на всех расстояниях, если обеспечим непрерывность линий, т. е. если уж линия вышла из заряда, то она никогда не кончится. На языке линий поля закон Гаусса утверждает, что линии могут начинаться только в плюс-зарядах и кончаться только в минус-зарядах. А число линий, покидающих заряд q, должно быть равно q/ε0.
 |
Сходную геометрическую картину можно отыскать и для потенциала φ. Проще всего изображать его, рисуя поверхности, на которых φ постоянно. Их называют эквипотенциальными, т. е. поверхностями одинакового потенциала.
Какова геометрическая связь эквипотенциальных поверхностей и линий поля? Электрическое поле является градиентом потенциала. Градиент направлен по самому быстрому изменению потенциала, поэтому он перпендикулярен к эквипотенциальной поверхности.
Если бы Е не было перпендикулярно к поверхности, у него существовала бы составляющая вдоль поверхности и потенциал изменялся бы вдоль поверхности и тогда нельзя было бы считать ее эквипотенциальной. Эквипотенциальные поверхности должны поэтому непременно всюду проходить поперек линий электрического поля.
У отдельно взятого точечного заряда эквипотенциальные поверхности — это сферы с зарядом в центре. На фиг. 4.12 показано пересечение этих сфер с плоскостью, проведенной через заряд.
В качестве второго примера рассмотрим поле близ двух одинаковых зарядов, одного положительного, а другого отрицательного. Это поле получить легко. Это суперпозиция (наложение) полей каждого из зарядов. Значит, мы можем взять две картинки, похожие на фиг. 4.12, и наложить их…
нет, это невозможно! Тогда получились бы пересекающиеся линии поля, а этого быть не может, потому что Е не может иметь в одной точке двух направлений. Неудобство картины линий поля теперь становится очевидным. С помощью геометрических рассуждений невозможно в простой форме проанализировать, куда пойдут новые линии. Из двух независимых картин нельзя получить их сочетание.
Принцип наложения, столь простой и глубокий принцип теории электрических полей, в картине полевых линий не имеет простого соответствия.
Картина полевых линий все же имеет свою область применимости, так. что мы можем все же захотеть начертить эту картину для пары равных (и противоположных) зарядов. Если мы вычислим поля из уравнения (4.13), а потенциалы из (4.23), то сумеем начертить и линии поля и эквипотенциали. Фиг. 4.13 демонстрирует этот результат. Но сперва пришлось решить задачу аналитически!
Эквипотенциальные поверхности

Всего получено оценок: 211.
Всего получено оценок: 211.
Одним из способов описания электрического поля являются эквипотенциальные поверхности. Рассмотрим подробнее смысл и метод построения таких поверхностей.
Потенциал электрического поля
Поскольку со стороны электрического поля на заряд действует сила, при перемещении заряда полем совершается некоторая работа (положительная, если заряд перемещается по направлению вектора силы, и отрицательная в противоположном случае). Следовательно, электрическое поле обладает некоторой потенциальной энергией.
Сила, действующая на заряд, пропорциональна этому заряду. А значит, потенциальная энергия поля также будет пропорциональна ему. Коэффициент пропорциональности, равный отношению потенциальной энергии поля к величине заряда, является энергетической характеристикой данного поля, и называется потенциалом:
Отметим, что потенциал пропорционален напряженности электрического поля, и численно равен работе, которая совершается, при удалении единичного заряда из этого поля (перемещения на бесконечное расстояние).
Эквипотенциальная поверхность
Если рассмотреть поле, создаваемое точечным зарядом, то его напряженность падает по мере удаления от заряда в любом направлении. Следовательно, по мере удаления происходит и уменьшение потенциала поля. При этом в пространстве вокруг заряда можно указать ряд точек, обладающих одинаковым потенциалом.
Напомним, что точки, равноудаленные от некоторой заданной, образуют сферу. А значит, точки вокруг точечного заряда, обладающие одним и тем же потенциалом, также будут образовывать сферу с центром, лежащим в точечном заряде. Важное свойство этой сферы – при перемещении заряда по ней работа поля равна нулю, поскольку потенциальная энергия во всех точках этой поверхности одинакова. Нулевая работа перемещения также следует из того факта, что вектор напряженности перпендикулярен этой сфере (а значит, и направлению перемещения).
Поверхность, образованная точками с одним потенциалом, называется эквипотенциальной. Силовые линии и эквипотенциальные поверхности всегда взаимно перпендикулярны, а значит, работа поля по перемещению заряда по эквипотенциальной поверхности равна нулю. Плотность расположения эквипотенциальных поверхностей характеризует скорость изменения потенциала в данной области. Чем гуще расположены эквипотенциальные поверхности, тем быстрее меняется потенциал при движении перпендикулярно им.
Для однородного поля, например, созданного двумя заряженными пластинами, эквипотенциальные поверхности представляют собой плоскости, параллельные пластинам. И в этом случае также перемещение заряда по любой поверхности равного потенциала происходит перпендикулярно вектору напряженности, а значит работа поля по перемещению равна нулю.
Для поля, образованного несколькими зарядами, эквипотенциальные поверхности имеют более сложную конфигурацию, однако, и в этом случае линии напряженности перпендикулярны этим поверхностям. Например, эквипотенциальные поверхности диполя выглядят следующим образом:
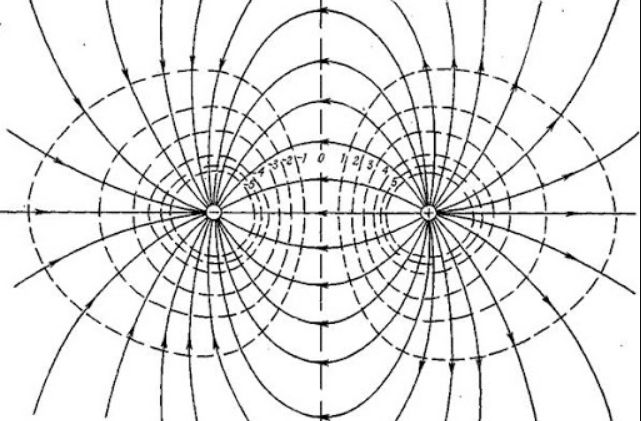
Отметим еще одно интересное свойство эквипотенциальных поверхностей – они могут располагаться плотнее и реже, но никогда не пересекаются.
Что мы узнали?
Потенциал электрического поля пропорционален его напряженности, и численно равен работе, которая совершается, при удалении единичного заряда из этого поля. Точки, в которых потенциал одинаков, образуют поверхность, называемую эквипотенциальной. При перемещении заряда вдоль этой поверхности работа поля равна нулю.
Эквипотенциальные поверхности
Вы будете перенаправлены на Автор24
Графическое изображение полей, можно составить не только с линиями напряженности, но и с помощью разности потенциалов. Если объединить в электрическом поле точки с равными потенциалами, то мы получим поверхности равного потенциала или как еще их называют эквипотенциальные поверхности. В пересечении с плоскостью чертежа эквипотенциальные поверхности дают эквипотенциальные линии. Изображая эквипотенциальные линии, которые соответствуют различным значениям потенциала, мы получаем наглядную картину, которая отражает, как изменяется потенциал конкретного поля. Перемещение вдоль эквипотенциальной поверхности заряда работы не требует, так как все точки поля по такой поверхности имеют равный потенциал и сила, которая действует на заряд, всегда перпендикулярна перемещению.
Следовательно, линии напряженности всегда перпендикулярны поверхностям с равными потенциалами.
Наиболее наглядная картина поля будет представлена, если изображать эквипотенциальные линии с равными изменениями потенциала, например в 10 В, 20В, 30 В и т.д. В таком случае скорость изменения потенциала будет обратно пропорциональна расстоянию между соседними эквипотенциальными линиями. То есть густота эквипотенциальных линий пропорциональна напряженности поля (чем выше напряженность поля, тем теснее изображаются линии). Зная эквипотенциальные линии, можно построить линии напряженности рассматриваемого поля и наоборот.
Следовательно, изображения полей с помощью эквипотенциальных линий и линий напряженности равнозначны.
Нумерация эквипотенциальных линий на чертеже
Довольно часто эквипотенциальные линии на чертеже нумеруют. Для того, чтобы указать разность потенциалов на чертеже, произвольную линию обозначают цифрой 0, возле всех остальных линий расставляют цифры 1,2,3 и т.д. Эти цифры указывают разность потенциалов в вольтах избранной эквипотенциальной линии и линии, которую выбрали нулевой. При этом отмечаем, что выбор нулевой линии не важен, так как физический смысл имеет только разность потенциалов для двух поверхностей, и она не зависит от выбора нуля.
Поле точечного заряда с положительным зарядом
Что очевидно из формулы, которая определяет потенциал поля точечного заряда при нормировке потенциала на бесконечность ($\varphi \left(\infty \right)=0$):
Система параллельных плоскостей, которые находятся на равных расстояниях друг от друга, является эквипотенциальными поверхностями однородного электрического поля.
Готовые работы на аналогичную тему
Задание: Потенциал поля, создаваемый системой зарядов, имеет вид:
Запишем уравнение (1.1) в каноническом виде:
Задание: Потенциал поля, имеет вид:
Перепишем уравнение (1.1) в виде:
Перепишем уравнение (1.1) в виде:
Мы получили каноническое уравнение двуполостного гиперболоида, его полуоси:
Перепишем уравнение (2.5) в виде:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 03 12 2021