генетические алгоритмы для обучения нейронных сетей
Применение генетических алгоритмов для обучения нейронных сетей
Авторы: Г.А. Поллак
Источник: Поллак Г.А. Применение генетических алгоритмов для обучения нейронных сетей / Поллак Г.А. // Издательский центр ЮУрГУ, 2011 год, С. 174–178
Генетические алгоритмы применяются для решения оптимизационных задач с помощью метода эволюции, т.е. путем отбора из множества решений наиболее подходящего. Они отличаются от традиционных методов оптимизации следующими свойствами [1]:
Генетические алгоритмы для обучения нейросети применяются как альтернатива методу обратного распространения ошибки. Целью обучения является минимизация функции стоимости E(n)= 1/2*ek 2 (n), где ek(n) = dk(n) – yk(n) – ошибка, dk(n) – желаемый выход нейросети, yk(n) – реальный выход нейросети, n – номер итерации.
Обучение методом обратного распространения ошибки сводится к подбору значений весов прямонаправленной нейронной сети, основываясь на принципах наискорейшего спуска. Один из основных недостатков этого классического алгоритма состоит в возможном попадании в локальные минимумы функции стоимости.
Применение генетического алгоритма позволяет избежать этой опасности. Рассмотрим в качестве примера нейронную сеть, которая реализует операцию XOR(рис. 1).
Рисунок 1 – Нейронная сеть, реализующая операцию XOR
Для сети требуется подобрать оптимальные веса w11, w11, w12, w21, w22, w31, w33, w10, w20, w30, минимизирующиe значение целевой функции, определяемой среднеквадратичной погрешностью
Параметрами задачи являются веса, которые определяют точку пространства поиска и, следовательно, представляет собой возможное решение.
Блок-схема, реализующая классический генетический алгоритм, показана на рис. 2.
Рисунок 2 – Блок-схема классического генетического алгоритма
Таблица 1. Результаты расчетов
Как видно из табл. 1 длина двоичной кодирующей последовательности составляет 8 бит.
При кодировании действительных чисел в качестве значения гена берется целое число, определяющее номер интервала (используется код Грея). В качестве значения фенотипа примем число, являющееся серединой этого интервала.
Исходная популяция хромосом задается случайным образом (табл. 2).
Таблица 2. Исходная популяция хромосом
| Код Грея | Номер интервала | Левая граница | Правая граница | Среднее значение | ||
| w1 | 11001100G | CCh | 204 | 0,5922 | 0,6000 | 0,5961 |
| w12 | 01100010G | 62h | 98 | 0,2392 | 0,2314 | 0,2353 |
| w21 | 00110011G | 33h | 51 | 0,6078 | 0,6000 | 0,6039 |
| w22 | 01110111G | 77h | 119 | 0,0745 | 0,0667 | 0,0706 |
| w31 | 00100010G | 22h | 34 | 0,7412 | 0,7333 | 0,7373 |
| w32 | 01010101G | 55h | 85 | 0,3412 | 0,3333 | 0,3373 |
| w10 | 01100010G | 62h | 99 | 0,2314 | 0,2235 | 0,2275 |
| w20 | 10100010G | A2h | 162 | 0,2627 | 0,2706 | 0,2667 |
| w30 | 00101010G | 2Ah | 42 | 0,6784 | 0,6706 | 0,6745 |
Отклик сети на входные сигналы y1 = 0,4592, y2= 0,2631, y3 = 0,3463, y4= 0,3551, среднеквадратичная ошибка Е = 0,2704. При вычислении выходных значений нейросети использовалась логистическая функция акти- вации с параметром скорости обучения η= 1.
Наибольшую роль в успешном функционировании алгоритма играет этап отбора родительских хромосом для создания новой популяции. Наиболее часто используется метод отбора, называемый рулеткой. Однако вследствие некоторых недостатков [1] этот метод плохо приспособлен для решения задачи минимизации. Поэтому предлагается использовать турнирный метод. Суть метода заключается в следующем. Все особи популяции разбиваются на подгруппы по 2–3 особи в каждой. Выбор родителей осуществляется случайно с вероятностью, меньшей 1.
В классическом генетическом алгоритме применяются два основных генетических оператора: оператор скрещивания и оператор мутации. Веро- ятность скрещивания достаточно велика (обычно 0,5 ≤ рс ≤ 1), вероятность мутации устанавливается весьма малой (чаще всего 0 ≤ рm ≤ 0,1). Это означает, что скрещивание в классическом алгоритме производится практически всегда, тогда как мутация – достаточно редко.
Оператор скрещивания действует следующим образом.
Рисунок 3 – Схема скрещивания
Оператор мутации с вероятностью рm изменяет значение гена в хромосоме на противоположное. Вероятность мутации может вычисляться случайным выбором числа из интервала [0, 1] для каждого гена и отбором для выполнения этой операции тех генов, для которых разыгранное число оказывается меньше или равным значению рm.
Хромосомы, полученные в результате применения генетических операторов к хромосомам временной родительской популяции, включаются в состав новой популяции. Она становится текущей популяцией для данной итерации генетического алгоритма. На каждой очередной итерации рассчитывается значение функции приспособленности для всех хромосом этой популяции, после чего проверяется условие остановки алгоритма. В качестве такого условия применяется либо ограничение на максимальное число эпох функционирования алгоритма, либо определяется сходимость алгоритма путем сравнения значений функции приспособленности популяции на нескольких эпохах. При стабилизации этого параметра алгоритм останавливается.
Следует подчеркнуть, что алгоритм обратного распространения ошибки, как правило, выполняется быстрее генетического, который просматривает все множество возможных решений. Однако градиентный метод не всегда приводит к ожидаемому результату, который зависит от выбора начальной точки. Кроме того, принципиальным недостатком метода обратного распространения ошибки является «застревание» в локальных оптимумах. Можно предложить гибридный метод обучения нейронных сетей, когда генетический алгоритм применяется для выбора начальной точки (исходного множества весов на каждой итерации), а затем применяется метод обратного распространения ошибки. Гибридный метод может позволить найти глобальное решение за приемлемое время.
Генетические алгоритмы для обучения нейронных сетей
Рассмотрим математическую модель поставленной задачи. Дан вектор X с размерностью 256, который представляет собой закодированное изображение известного распознаваемого символа. Также есть вектор Y с размерностью 10, который отражает требуемый результат распознавания, указывающий принадлежность символа к эталонному образцу. Необходимо найти весовую матрицу W, элементами которой являются вещественные числа в отрезке [0; 1], чтобы выполнялось равенство:
Необходимо осуществить настройку весовой матрицы W с помощью генетического алгоритма. В рамках решаемой задачи рассматриваемая матрица имеет следующую размерность: количество строк равняется 10, что представляет собой все символы, описывающие арабские цифры; количество столбцов определяется размером знакоместа, отводимого под каждый символ, 256 столбцов.
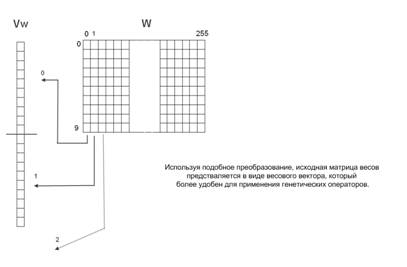
С точки зрения очевидности и простоты понимания следует каждый столбец матрицы весов рассматривать в качестве хромосомы, что приведет к наличию 256 хромосом, которые в совокупности будут отражать каждую особь. Однако при практической реализации гораздо удобнее использовать более простую структуру, хотя и менее наглядную. Это связано с тем, что довольно тяжело реализовать операции кроссинговера и мутации при наличии нескольких хромосом. Каждая особь в разрабатываемом генетическом алгоритме можно представить в виде только одной хромосомы, что значительно упростит программную реализацию на ЭВМ. Этого можно достичь следующим способом. Хромосома будет начинаться с первого столбца матрицы весов, и каждый следующий столбец будет просто добавляться в конец уже существующей «единой» хромосомы. Данный метод проиллюстрирован на рисунке 1.
Рис. 1. Преобразование весовой матрицы W в вектор весов Vw.
Классический генетический алгоритм состоит из ряда наиболее важных этапов. Фактически данные этапы можно расположить в хронологическом порядке.
Все описанные этапы являются абсолютно справедливыми в рамках решаемой задачи 2. Практическая реализация первого шага любого генетического алгоритма в большинстве случаев представляет собой не что иное, как инициализацию случайным образом. Каждому гену любой хромосомы присваивается случайное значение из интервала допустимых значений. Соответственно, при настройке весовой матрицы W каждый ген получит генетическую информацию в виде случайного значения в отрезке [0; 1]. Программная реализация подобного метода инициализации является самой простой и имеет свои достоинства и недостатки. Достоинства заключаются в следующем.
Оценка приспособленности особей в популяции заключается в вычислении значения функции пригодности для каждого члена популяции. И чем выше это значение, тем больше особь отвечает требованиям решаемой задачи. В рамках решаемой задачи весовая матрица есть часть нейронной сети, которая осуществляет распознавание образов. И соответственно генетический алгоритм выполняется на стадии обучения нейронной сети. Иными словами, необходимо привести весовую матрицу к такому виду, при котором ошибка распознавания эталонного образа будет минимальной. Таким образом, функция пригодности оценивает ошибку распознавания каждого эталонного образа, и чем меньше ошибка, тем выше значение функции пригодности. Задача состоит в минимизации ошибки распознавания. Для этого необходимо сравнить полученный вектор Y′ с эталонным образцом Y.
Этап селекции предусматривает выбор тех особей, генетический материал которых будет участвовать в формировании следующей популяции решений, т.е. в создании очередного поколения. Описываемый выбор производится согласно принципу естественного отбора, благодаря которому максимальные шансы имеют особи с наибольшими значениями функции пригодности. Различают достаточно большое множество методов селекции. Одним из самых известных и часто применяемых является метод «рулетки». Такое название интуитивно помогает понять его принципы. Каждая особь получает определенный сектор на «колесе», размер которого напрямую зависит от значения функции пригодности.
Отсюда вытекает, что чем выше значение функции пригодности, тем больше будет размер сектора на «колесе рулетки». Очевидно, что чем больше сектор, тем выше вероятность «победы» соответствующей особи. И, как следствие, вероятность выбора определенной особи оказывается пропорциональной значению ее функции приспособленности. Использование метода «рулетки» часто приводит к преждевременной сходимости алгоритма, которая заключается в том, что в популяции начинают доминировать лучшие особи, но не оптимальные. Спустя несколько поколений популяция практически полностью будет состоять из копий наиболее лучших особей. Однако весьма маловероятно, что достигнутое решение будет оптимальным, так как исходная популяция генерируется случайным образом и представляет собой лишь малую часть пространства поиска. Чтобы предотвратить преждевременную сходимость генетического алгоритма, используется масштабирование функции приспособленности. Масштабирование функции пригодности позволяет исключить ситуацию, когда средние и лучшие особи начинают формировать одинаковое число схожих потомков в следующих поколениях, что является крайне нежелательным явлением. Следует отметить, что масштабирование также предупреждает случаи, когда, несмотря на значительную неоднородность популяции, среднее значение функции приспособленности мало отличается от максимального. Итак, масштабирование функции приспособленности есть не что иное, как преобразование ее вида. Выделяют три основных преобразования: линейное, степенное и сигма-отсечение. В разработанном алгоритме используется преобразование сигма-отсечение.
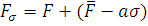
Также можно в определенной степени модифицировать данный метод селекции или строить селекцию на основе синтеза сразу нескольких методов.
Следующим этапом генетического алгоритма является рекомбинация или кроссинговер. Каждый участок хромосомы особи заключает в себе определенную информационную нагрузку. Целью рекомбинации является получение такой комбинации промежутков хромосом, при которой особь будет представлять собой наилучшее из решений, возможное при текущем генетическом материале. В итоге основной задачей операции кроссинговера является получение в конечном итоге наиболее функциональных признаков, которые присутствовали в наборах исходных решений. Подобный механизм решения оптимизационных задач, в отличие от существующих методов, не осуществляет замену одного решения на другое, а получает новые возможные решения посредством обмена информацией между ними.
Скрещивание является наиболее важным оператором генетического алгоритма, так как именно с помощью оператора кроссинговера осуществляется обмен информацией между решениями. Потомки содержат в себе комбинацию специфических особенностей обоих родителей. Эффективность работы любого генетического алгоритма находится в прямой пропорциональной зависимости от эффективности операции кроссинговера. Кроме того, производительность генетического алгоритма зависит от успешности работы кроссинговера в первую очередь. В рамках решаемой задачи реализован упорядоченный оператор кроссинговера. Упорядоченный кроссинговер осуществляет поэтапное рутинное преобразование генетического материала, приближаясь к оптимальному решению.
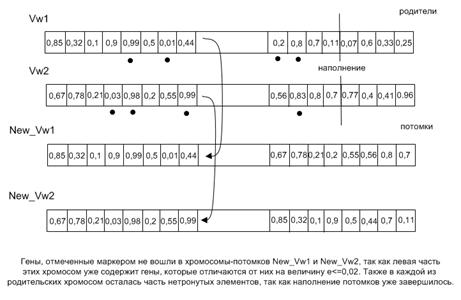
На рис. 2 изображен процесс получения новых особей с использованием упорядоченного кроссинговера. Имеются две родительские хромосомы: Vw1 и Vw2. Генетическим материалом являются вещественные числа от 0 до 1. Упорядоченный кроссинговер работает следующим образом. Изначально случайным образом определяется «разрезающая точка». На следующем этапе первый потомок New_Vw1 наследует левую часть родительской хромосомы Vw1. Заполнение оставшихся генов новой хромосомы осуществляется за счет информации, хранящейся у второго родителя Vw2. Алгоритм просматривает хромосому Vw2 с самого начала и осуществляет извлечение генов, которые отличаются от генов, уже находящихся в потомке, более чем на величину e = 0,02. Малая величина e задается в алгоритме для определения «родства» генов. С каждым последующим шагом, а в особенности на завершающих этапах алгоритма, имеет смысл уменьшать значение этой величины для достижения более точных результатов. Аналогичная процедура выполняется при получении второго потомка New_Vw2. Второй потомок New_Vw2 наследует левую часть родительской хромосомы Vw2. Заполнение оставшихся генов получаемой хромосомы осуществляется за счет информации, находящейся у второго родителя Vw1.
Рис. 2. Принцип работы упорядоченного кроссинговера.
Алгоритм производит анализ хромосомы Vw1 с первого гена и осуществляет упорядоченное извлечение генов, которые отличаются от генов, уже находящихся в потомке, более чем на величину e = 0,02. В результате работы каждого оператора скрещивания в популяции появляются две новые особи. Чтобы контролировать количество операций кроссовера используется коэффициент скрещивания Kk, определяющий долю производимых на каждой итерации потомков. Количество потомков определяется следующей формулой:
Высокое значение коэффициента скрещивания Kk позволяет увеличить количество областей пространства поиска и уменьшает опасность попадания в локальный оптимум, однако слишком большое значение указанного параметра приведет к увеличению времени работы алгоритма, а также к чрезмерному исследованию малоперспективных областей поискового пространства.
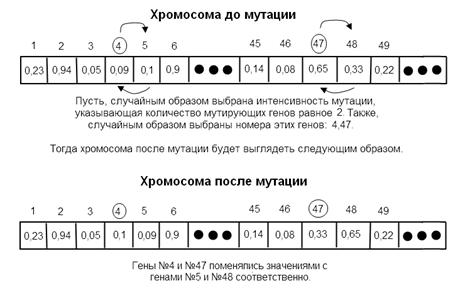
Следующим этапом генетического алгоритма является мутация. Мутация есть изменение, которое приводит к проявлению качественно новых свойств генетического материала. Мутации происходят случайным образом и вызывают скачкообразные изменения в структуре генотипа.
Рис. 3. Случайная мутация на основе приращения.
Использование в одном алгоритме сразу нескольких видов оператора мутации позволяет осуществить эффективный поиск оптимального решения. Что позволяет в течение короткого промежутка времени получить неплохие результаты, а также выделить наиболее пригодные для изучения «окрестности решений».
Оператор мутации применяется к потомкам особей, получаемых после операции скрещивания. Особи с мутациями остаются в популяции до начала этапа «формирование новой популяции». Количество мутирующих особей определяется формулой:
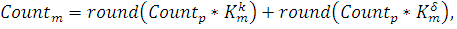
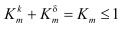
Рис. 4. Классический многоточечный оператор мутации.
Следующим этапом разработанного генетического алгоритма является формирование новой популяции. Насколько сильно выросла численность популяции, определяется общим коэффициентом мутации Km и коэффициентом скрещивания Kk. В общем виде текущая численность популяции вычисляется по следующей формуле:
Определение критерия остановки генетического алгоритма напрямую зависит от специфики решаемой задачи и имеющихся сведений об объекте поиска. В большинстве оптимизационных задач, для которых известно оптимальное значение функции пригодности, остановку алгоритма можно организовать при достижении наилучшей особью этой величины, возможно с некоторой погрешностью. Решаемая задача на самом деле не располагает сведениями об оптимальном значении функции пригодности. Иными словами, алгоритм стремится максимизировать функцию пригодности с учетом того, что ошибка распознавания стремится к нулю. Поэтому в созданном алгоритме реализован механизм остановки поиска, основанный на отсутствии изменения функции пригодности наилучшей особи в течение определенного числа итераций, которое задается в качестве параметра генетического алгоритма. Кроме этого, алгоритм предусматривает остановку своей работы по истечении определенного числа итераций, которое также задается в качестве параметра. В том случае, если условие остановки выполнено, то алгоритм выдает в качестве оптимального решения то, которое представлено наилучшей особью, определенной на этапе формирования новой популяции. Если же условие не выполнено, то алгоритм передает управление этапу селекции.
Таким образом, в результате работы генетического алгоритма получен набор весовых коэффициентов, обеспечивающих корректную работу нейронной сети. Также стоит отметить тот факт, что использование специального оператора мутации позволило сократить время обучения сети. Для обучения было выбрано обучающее множество из 180 элементов. Время обучения на этом множестве с помощью описанного генетического алгоритма с использованием мутации на основе приращения, нечеткой сети Ванга-Менделя составило 2 мин. 50 сек., обучение с использованием алгоритма с применением классического многоточечного оператора мутации длилось 3 мин. 10 сек., а применение гибридного оператора мутации позволило сократить время обучения до 1 мин. 20 сек. Таким образом, полученный генетический алгоритм позволяет сократить время поиска наилучшего решения в рамках поставленной задачи.
Нейронные сети, генетические алгоритмы и прочее… Мифы и реальность. Версия II
Прежде всего, я хотел бы поблагодарить всех, кто дал свои критические комментарии по первой версии статьи. Мне показалось, что написать версию два, а не просто оставить все как есть, было бы правильной идеей.
Конечно же, искусственный интеллект уже существует! Если посмотреть заголовки статей в популярных СМИ, названия и слоганы различных научных конференций на эту тему – безусловно это так. Нельзя не поверить, особенно когда очень этого хочется наконец-то оказаться в XXI веке — «настоящем», как это описывалось во всех научно-фантастических романах. Но так ли это? А если нет, то что существует на самом деле. В попытке разобраться в мифах и реалиях была написана эта статья.
Первоначально хотелось начать как-то так: «впервые упоминание термина «Искусственный интеллект» появилось у Д. Мккарти в 1956 году на конференции в Дартмундском университете, основоположниками ИИ следует считать У.Мак-Каллока, У.Питса, Ф.Розенблата» и т.д. Однако, это уже слишком поздно и не совсем отвечает целям статьи, да и википедия опередила с таким началом.
Анализируя последние «победы» ИИ, а также критические статьи неизбежно приходишь к выводу, что все крутится вокруг нескольких общих особенностей. Одна часть статей критикует невозможность прохождения тестов, а другая полна патетики о «невероятных победах». При этом игнорируется тот факт, что победы были достигнуты в узкоспециализированных задачах, где основным преимуществом машины была скорость переборов по базе фактов и «умении» видеть закономерности там, где человек просто-напросто быстро устает это делать. Блестящие примеры кластерного анализа в том или ином виде и формирование базы шаблонов-фактов. Всё это следствия, причины же в большинстве случаев или не анализируются совсем, или рассматриваются поверхностно.
Бесспорно, что на сегодняшний день ИИ можно признать отдельной наукой или, как минимум, отдельной отраслью знаний. Любая наука должна обладать собственной аксиоматикой, определениями, теоремами и гипотезами. И вот здесь и начинается самое интересное. А именно – с определения того, какую же деятельность можно назвать «интеллектуальной» и что можно охарактеризовать как «искусственный интеллект»? Далее необходимо обозначить перечень причин и условий, на основании которых можно или нельзя констатировать факт существования искусственного интеллекта в его полной форме, например, по Серлу. Неопределенность же в этих вопросах и порождает весь тот огромный спектр мифов, которым оброс ИИ. Кроме того, существует целый ряд неплохих статей по истории возникновения ИИ, например, вот или вот. Но все же, немного погрузится в историю стоит еще раз было бы целесообразным.
Начнем с определения того, что же такое ИИ, попробуем проследить дрейф самого понятия. Некоторые даты являются приблизительными.
1956 год. Д. Маккарти предлагал, что «под интеллектом в пределах этой науки понимается только вычислительная составляющая способности достигать целей в мире», а вместо понятия программное обеспечение – вычислительные методы.
1976 год. Гипотеза Ньюэлла-Саймона о том, что способность выполнять символьные вычисления вполне достаточна для того, чтобы стать способным выполнять осмысленные действия. Следовательно, все животные и человек по сути выполняют символьные вычисления. В известной мере это продолжении механицизма Декарта и его Картезианской теории. Все современные исследования строятся именно на этой гипотезе, не смотря на всю ее критику.
1971-79 год. Эдвард Фейгенбаум создает концепцию экспертных систем, ставшую прототипом всех экспертных систем. По сути, произошел переломный момент, после которого современная тенденция использования статистики как основы обучения окончательно закрепилась в качестве основной. Исследования в области эвристики были окончательно вытеснены на обочину.
1980 год. Первая развилка. Джон Серл предложил такие понятия как сильный (полный) и слабый ИИ. «…такая программа будет не просто моделью разума; она в буквальном смысле слова сама и будет разумом, в том же смысле, в котором человеческий разум — это разум».
1981 год. Барр и Файгенбаум определили, что искусственный интеллект— это область информатики, которая занимается разработкой интеллектуальных компьютерных систем, т.е. систем, обладающих возможностями, которые мы традиционно связываем с человеческим разумом, — понимание языка, обучение, способность рассуждать, решать проблемы и т.д.
1989-1995 год. Возникновение термина «интеллектуальный агент». Примером может послужить работа Рассела и Норвига[1].
2004 год. Осипову Г.С.[2] принадлежит одно из наиболее точных, с точки зрения автора, определений термина и задач ИИ. Он определил ИИ как набор методов, моделей и программных средств, позволяющих искусственным устройствам реализовать целенаправленное поведение и разумные рассуждения.
Суммируя все вышесказанное, хочется вспомнить замечание Бертрана Рассела: все что кажется определенным и точным при более пристальном взгляде становится неопределенным. Современное понимание термина ИИ по факту все больше уходит к интерпретации ИИ как программных средств или Интеллектуальных агентов (ИА). Основным предназначением является решение определённого класса задач в тесном переплетении с Big Data как источника фактов для анализа. В качестве примера можно привести задачу перевода. При всей своей кажущейся всеобъемлемости, она ограничена задачами сопоставления, но совершенно не решает задачу ответов на вопросы: «какая гора самая высокая?» или «что делать если…»!
Таким образом, явно наблюдается дрейф задачи в область узкоспециализированных систем-агентов и о фактическом уходе от задачи построения ИИ-полной модели в сторону специализированных интеллектуальных агентов. Это неплохая новость, так как отодвигает вероятность катастрофы, описанной Ником Бостромом, а само понятие «интеллектуальный» становится простой декорацией.
Что же касается основных этапов, в свое время попавшаяся на глаза хронология неплохо описывает основные этапы становления ИИ, к сожалению автор неизвестен:
Этап 1 (50–е годы) (Нейрон и нейронные сети)
Он связан с появлением первых машин последовательного действия, с очень небольшими, по сегодняшним меркам, ресурсными возможностями по памяти, быстродействию и классам решаемых задач. Это были задачи сугубо вычислительного характера, для которых были известны схемы решений и которые можно описать на некотором формальном языке. К этому же классу относятся и задачи на адаптацию.
Этап 2 (60-е годы) (Эвристический поиск)
В «интеллект» машины добавились механизмы поиска, сортировки, простейшие операции по обобщению информации, не зависящие от смысла обрабатываемых данных (в этом месте трудно согласится с автором в полной мере). Это стало новой точкой отсчета в развитии и понимании задач автоматизации деятельности человека.
Этап 3 (70-е годы) (Представление знаний)
учеными была осознана важность знаний (по объему и содержанию) для синтеза интересных алгоритмов решения задач. При этом имелись в виду знания, с которыми математика не умела работать, т.е. опытные знания, не носящие строгого формального характера и описываемые обычно в декларативной форме. Это знания специалистов в различных областях деятельности, врачей, химиков, исследователей и т.п. Такие знания получили название экспертных знаний, и соответственно системы, работающие на основе экспертных знаний, стали называться системами-консультантами или экспертными системами.
Этап 5 (90-е годы) (Автоматизированные обрабатывающие центры)
Усложнение систем связи и решаемых задач потребовало качественно нового уровня «интеллектуальности» обеспечивающих программных систем, таких систем, как защита от несанкционированного доступа, информационная безопасность ресурсов, защита от нападений, смысловой анализ и поиск информации в сетях и т.п. И новой парадигмой создания перспективных систем защиты всех видов стали интеллектуальные системы. Именно они позволяют создавать гибкие среды, в рамках которых обеспечивается решение всех необходимых задач.
Этап 6 (2000-е годы) (Робототехника)
Область применения роботов достаточно широка и простирается от автономных газонокосилок и пылесосов до современных образцов военной и космической техники. Модели оборудованы навигационной системой и всевозможными периферийными датчиками.
Этап 7 (год 2008) (Сингулярность)
Создание искусственного интеллекта и самовоспроизводящихся машин, интеграция человека с вычислительными машинами, либо значительное скачкообразное увеличение возможностей человеческого мозга за счёт биотехнологий.
По некоторым прогнозам, технологическая сингулярность может наступить уже около 2030 года. Сторонники теории технологической сингулярности считают, что, если возникнет принципиально отличный от человеческого разум (постчеловек), дальнейшую судьбу цивилизации невозможно предсказать, опираясь на человеческое (социальное) поведение.
Вернемся к проблемам и мифам, которые возникли во многом благодаря большому количеству писателей, а также в попытке разных команд разработчиков получить инвестирование их исследований. В целях разоблачения мифов, написано и опубликовано не меньше статей. Примером могут послужить такие статьи как эта или эта, а вот одна из лучших по образности изложения статей и т.д… Писать очередную статью, на первый взгляд – довольно спорное занятие, если не обратить внимание на некоторые общие черты. Общей чертой всех этих работ является констатация того факта, что все они строятся вокруг критики возможностей нейронных сетей, а также того факта, что мы не знаем, как работает мозг, и что строить ИИ не обязательно вокруг идеи невральных моделей. Все это верно, но практически никто из авторов не пытается сформулировать что-же необходимо для решения задачи ИИ. В рамках настоящей статьи хотелось бы, пусть и условно, но попытаться обозначить задачи, без решения которых невозможно двигаться дальше.
Прежде чем продолжить хотелось бы сделать несколько замечаний.
Во-первых, исключить разговоры о тайных исследовательских центрах, в которых какие-то силы скрывают истинное положение дел. Создание действительно разумного агента требует разрешения целого ряда философских проблем и разработки на основании этих решений нового математического аппарата, что попросту невозможно скрыть в полном объеме.
Во-вторых, все дальнейшие рассуждения ни в коем случае не являются неким утверждением о «божественности» или «непознаваемости» человеческой природы. Задача данной статьи показать белые пятна и показать факт излишней оптимистичности заявлений о факте существования ИИ в его полном виде на сегодняшний день.
Что же представляют собой существующие технологии? Общий пул технологий, объединенных под общим термином «системы искусственного интеллекта» не так уж и велик. К нему с разной степенью достоверности можно отнести:
Согласно Википедии, да простится ссылка на нее, нейронные сети «представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов)». Красиво. Существуют различные варианты реализации такие как байесовские сети, рекуррентные сети и т.д… Основная модель работы: база образов-передаточная функция-оптимизатор.
Наибольшее распространение сегодня получили ограниченные машины Больцмана в многослойном варианте. Многослойность, т.е. глубина необходима для преодоления проблемы «XOR». Кроме того, как показано Хинтоном, рост количества слоев скрытых нейронов позволяет увеличить точность за счет наличия «промежуточных» образов с минимальным отличием в каждом слое. При этом, чем ближе промежуточный слой к выходу, тем выше конкретизация образа.
Основная цель создания нейронных сетей и вытекающая из этого задача обучения — это избавление от необходимости промежуточных вычислений-выводов при анализе профиля-матрицы входящих сигналов. Данная цель достигается за счет создания базы эталонных профилей, каждому из которых на выходе должен соответствовать единственный нейрон – ячейка результирующей матрицы. Каждому такому нейрону приписывается определенная трактовка-результат.
Основная проблема как с точки зрения решаемой задачи, так и собственно обучения – это зашумленность поступающих на анализ профилей-матриц возбужденных нейронов входящего слоя. Поэтому одним из основных условий является наличие качественной обучающей выборки. Если обучающая выборка низкого качества, то сильная зашумленность приведет к большому количеству ошибок. Впрочем, и большой размер обучающей выборки может привести к тому же результату.
В какой-то степени, работу нейронной сети можно сопоставить с работой безусловных рефлексов живых существ[3] со всеми вытекающими недостатками.
Такой подход отлично работает для задач где отсутствует сильная зашумлённость, четкая априорная база эталонных образов. Основной задачей является выбор наиболее подходящего образа из уже существующей базы знаний. Задачи прогнозирования, в данном случае, будут решаться только путем экстраполяции существующей истории без возможности создания новых сущностей т.е. индукцией с недостаточной дедукцией.
Кто-то может поспорить что это не так. Но прежде чем отметать вышесказанную мысль необходимо определится в том, что имеется ввиду под термином «новая сущность»? Это еще один экземпляр в рамках существующего пространства классов-векторов выбранной предметной области или создание новых областей-пространств? Теме сравнения чего-либо с чем-либо, что можно сравнивать и что нельзя, проблеме смешения предметных областей будет посвящена одна из следующих статей.
Основной принцип обучения у человека — это индукция и абдукция. Индукция затруднена хотя бы из-за изначальной постановки задачи – избавится от промежуточных вычислений. Возможное возражение о том, что процессы, связанные с индукцией, могут происходить на этапе обучения — являются слабыми, так как обучение строится на нескольких основополагающих принципах:
Согласно все той же Википедии: «Генетический алгоритм (англ. genetic algorithm) — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, аналогичных естественному отбору в природе».
Существует масса работ таких авторов как Панченко Т.В[4]., Гладкова Л. А., Курейчика В. В[4] и т.д… Основы «генетического подхода» хорошо раскрыты здесь, множество интересных работ, посвященных применению генетических алгоритмов. Например, работа Плешакова И.Ю., Чуприной С.И.[5], статья Иванова В.К. и Манкина П.И.[6], статьи на хабре и ряд других.
Одним из наиболее важных преимуществ генетических алгоритмов является отсутствие необходимости информации о поведении функции и незначительное влияние возможных разрывов на процессы оптимизации. Как и в случае нейронных сетей, происходит уход от необходимости анализа причинно-следственных связей, путем построения «итогового» образа — целевой функции. В этом смысле, с точки зрения решения анализа текста, поиска генетические задачи решают такие же задачи или очень похожие, что и методы латентно-семантического анализа. При этом, надо отдать должное, в вопросах семантического поиска и индексации текстов генетические алгоритмы имеют гораздо большие перспективы, по сравнению методами латентно-семантического анализа.
С точки зрения распознавания образов, с очень сильной натяжкой целевую функцию можно сравнить со слоем входных нейронов и с ожиданием максимума как аналога максимизации сигнала нейрона выходного слоя. Хотя правильнее было бы говорить, что генетические алгоритмы используются для повышения эффективности обучения нейронных сетей, но все же не могут рассматриваться как конкуренция нейронными сетям. Задачи разные.
Общий же недостаток — отсутствие индукционных алгоритмов — присутствует в полной мере.
ДСМ-метод автоматического порождения гипотез, предложенный В.К.Финном [Финн, 1983], представляет собой синтез познавательных процедур индукции, аналогии и абдукции [Финн, 1999]. Он может быть сформулирован в виде системы правил и даже представлен в виде программы на языке логического программирования [Виноградов, 1999], [Виноградов, 2001], [Efimova et al, 2006].[7]
Условие насыщения будет выполнено, если применение процедуры индукции не приводит к порождению новых гипотез. Проверка на каузальную полноту как раз и представляет собой применение некоторого варианта абдукции. Набор данных и вариант стратегии ДСМ-метода удовлетворяют условию каузальной полноты, если все данные о наличии или отсутствии свойств у объектов объясняются с помощью гипотез о возможных причинах наличия или отсутствия свойств, порожденных с помощью процедуры индукции.
Если условие каузальной полноты не выполнено, то это является основанием для пополнения базы фактов и/или изменения стратегии ДСМ-метода и/или способа представления данных. Все эти операции выполняются при участии человека. С точки зрения В.К. Финна[8] наиболее перспективным в данном вопросе является дальнейшее развитие именно ДСМ-методов.
К этому перечню можно было бы добавить пару-тройку технологий, но это не повлияло бы на картину в целом.
Таким образом, сегодня под термином «ИИ» скорее подразумевается подвид технологических (алгоритмических) подходов к решению задач комбинаторики. Основными задачами которого являются достоверное отделение «статически значимых» по своей сути закономерностей и построение на основе статистики образов-объектов, без анализа причинно-следственных связей. Основные направления — это распознавание образов. Под образами можно понимать изображения, звуки, совокупность симптомов болезней и т.д.
Результатом обучения нейронной сети и т.д. должна быть некая выявленная закономерность, представленная в виде некой матрицы-кластера (вектора). Безусловно, эта матрица или множество может постоянно корректироваться за счет новых примеров, но это не влияет на суть происходящего. В любом случае, выявленное и очищенная от шума множество может быть представлена в виде «отчуждаемой логики», которая представляет собой некий «оптимальный» способ решения задачи. Примером такой области может служить задача автоматической рубрикации текстов, но не сточки зрения разнесения текстов по уже известным рубрикам, а собственно само создание рубрик. Их аннотирование, а также автоматическое построение различного рода онтологий.
По мнению большинства специалистов, все эти методы являются не более чем реинкарнациями задач статистики и кластеризации. Следовательно, все современные усилия в области глубокого машинного обучения и т.д. не более чем усилия энтомологов по изучению бабочек. Поиск и описание отличий цвета и формы крыла не дают ни малейшего понимания природы полета. При этом следует признать, что они весьма полезны с точки зрения распознавании образов как визуальных, так и других подобных объектов, будь то истории болезней или анализ шахматных партий…
Все это приводит к выводу, что дальнейшие рассуждения в направлении исследований физической или «невральной» модели построения ИИ являются тупиковыми. Все дальнейшие рассуждения необходимо строить на базе логических абстракций таких как определение того, что же такое интеллект, какие признаки, какая «механика» процессов дедукции, индукции, абдукции. Какова логика и математика основных законов логики. Какие логики и математики необходимо, скажем так, «изобрести» для создания ИИ. Что же необходимо для решения ИИ-полной задачи? Для начала, необходимо определится с термином «интеллектуальный», «интеллект» и какими признаками он должен обладать.
Что же считать интеллектом и тем более искусственным? И здесь начинают возникать первые трудности. Например, считать ли интеллектуальными системы, созданные для решения конкретных задач, обладающие возможности к логическим выводам и самообучению в рамках поля задач. Если же считать ИИ системой, способной к самосознанию и целеформированию, то можно ли считать правильным термин «искусственный»? Ведь в этом случае мы будем иметь дело со вполне самостоятельной личностью, пусть и имеющую другую физическую природу. Все же «искусственный» это не просто рукотворный, а скорее ограниченный искусственными границами. Иначе, в некотором роде все люди являются рукотворными, так как создаются другими людьми.
К сожалению, все философские определения в силу своей недостаточной «механистичности» не дают достаточную базу для решения задач построения ИИ.
С точки зрения понимая задач ИИ, более близкими оказываются определения из биологии и психологи. В большинстве своем они сводятся к тому, что Интеллект — это вид адаптационного поведения, направленного на достижение цели. Достижение целей и адаптация у всех исследователей ставится во главу угла. Анализ механизмов целеуказания является сам по себе темой отдельной стати, поэтому пока ограничимся фактом ее наличия.
Сточки зрения задач алгоритмизации и построения логик большой интерес представляют работы Джоя Пола Гипфорда, предложившего еще в 1950-х годах кубическую модель структуры интеллекта. Что примечательно, всемирную известность ему принесли исследования, в которых он, на основе использования тестов и факторного анализа, предпринял попытку математического построения модели творческой личности.

Структура интеллекта по Дж. П. Гипфорду.
Отдельно следует выделить А. Тюринга с его работой «Может ли машина мыслить» и машиной-ребенком.
Встречающиеся в разных работах свойства интеллекта могут быть уже более конкретным и понятным с точки зрения алгоритмов и моделей построения ИИ. Так встреченный список существенных качеств человеческого интеллекта, может быть довольно интересен. К ним относятся:
Начинать рассуждения о проблемах математической логики при создании ИИ следовало бы с формализованного представления таких понятий как «ценность», «смысл», «полезность», «этичность» и т.д… Фактически до сих пор отсутствуют решения вопросов формализации смысла, индукции и другие сложные логико-философские вопросы. Например, что такое знание, как оно устроено и как связано с фактами. Как исчислять выводы на основании знаний? Что такое знак и что такое минимальная единица смысла? Как оперировать предикатами более чем первого порядка? К сожалению, современные понимания этих понятий неизбежно сводятся к каким-либо функциям, кластеризации, максимизации или минимизации каких-либо целевых параметров. При этом желательно дифференцируемость пространства. В действительности же процессы мышления не дифференцированы, а скорее представляют собой нечто похожее на фракталы с инно- и самореференциями. В этом смысле довольно любопытны, например, работы Умберто Матураны с его автопоэзисом[10], Тарасенко В.В.[11] или работы В.Ф. Турчина, которым в 1966 году был разработан язык рекурсивных функций Рефал. Рефал был предназначен для описания языков и разных видов их обработки.
Как точно подмечено Пантнэмом[12]: «понятия… это не образы и не ментальные репрезентации… а скорее способности и навыки, создающие возможности для оперирования знаками для единства нашего поведения и знаковых систем». А выражаясь языком математики, замечательно выраженное Мандельбротом, мышление имеет аналогию фракталу. Форма фрактала не зависит не от образца или воспроизводимого в итерациях паттерна. Эта форма зависит от характера бесконечных итераций способа преобразований[13].
Оставив в стороне высокие материи, попробуем разобраться хотя бы с такими «базовыми» понятиями как «индукция», «абдукция», «дедукция». Определений всех этих терминов огромное количество, поэтому приведем некоторые и попробуем их прокомментировать. К сожалению, в рамках статьи невозможно подробно рассмотреть эти вопросы, иначе это была бы уже книга. Поэтому, придется ограничится поверхностным обзором некоторых проблем. Анализ таких понятий как «знание», «факт», «знак», тем более сточки зрения алгоритмов, требует отдельной статьи.
Дедукция– умозаключение от знания большей степени общности к новому знанию меньшей степени общности[14]. С точки зрения алгоритмизации, пожалуй, самое понятное и в полной мере реализованное понятие. Все современные рения в области ИИ, такие как нейронные сети, как раз и реализуют данную логику.
Индукция — умозаключение от знания меньшей степени общности к новому знанию большей степени общности. В математической логике это умозаключение, дающее вероятностное суждение[15]. Базовыми проблемами индукции, сформулированными Юмом еще в 1888 году и в некоторой степени решенные Поппером К. [16] еще/только/уже в 1933 году, были, например, такие: как обосновать веру в то, что будущее будет (в большой мере) таким, же, как и прошлое? Как можно оценить веру в справедливость ожиданий в будущем? Оправдан ли в наших рассуждениях переход от случаев, повторно встречающихся в нашем опыте, к другим случаям, с которыми мы раньше не встречались? Как математически учесть привычку, как неотъемлемую часть процесса индукции? Казалось бы, для этого существуют такие вещи как Байесовские вероятности т.д… Но если вдуматься, то они совершенно не дают ответа на эти вопросы. Невозможно повторяемость сделать главным фактором в индуктивном выводе и как участь иррациональность поведения? Это только часть проблем. Следовательно, математическая модель, основанная на «классической» статистике, здесь не работает в полной мере…
Закон абсолютности качества, сформулированный Гегелем и популистски перефразированный Энгельсом как закон перехода количества в качество. Во многом этот закон является уточнением предыдущей темы. Смысл закона в том, что количество наблюдений никак не связано с возникновением новых свойств. В данном случае Энгельс пошёл на фактическую фальсификацию ради своих идей. Так же, как и проблема индукции на сегодняшний день не имеет математического решения.
Абдукция – познавательная процедура принятия гипотез. Впервые явно выделена Ч.С. Пирсом, который рассматривал абдукцию (абдуктивный вывод) наряду с индукцией и дедукцией. Ч.С. Пирс считал, что, отбирая среди необозримого множества гипотез наиболее существенные, исследователи реализуют «абдукционный инстинкт», без которого невозможно было бы развитие науки[17]. Проблема заключается в том, что на сегодняшний день отсутствует математический аппарат, позволяющий рассчитать порог, да и сами правила принятия гипотез. Как понять, что определенная группа гипотез, объясняющих группы фактов являются «правдоподными»? Пирс считал способность человеческого мозга к таким операциям «абдуктивным инстинктом» человека. Какова математическая модель абдукторного мышления?
Одной из основных причин неудач формализации процессов мышления была сформулирована еще Кантом[18] как проблема «законченности» искусственных систем, в противоположность естественным, которые являются аморфными по своей структуре и логической «незаконченности». Таким образом, все эти понятия довольно сложные и до сих пор четко не сформулированные не только с позиций математической, но и философии как таковой. Без реализации этих проблем невозможно создание Интеллектуальных агентов, способных к решению общих задач. Но на сегодняшний день автору не известны такого рода логики. Несколько более оптимистичным выглядит утверждение Ника Бострома[19] о том, что «…прогресс на этом пути требует скорее технологических решений, чем технологических прорывов…».
Тем не менее, существует несколько замечательных исследований, таких как работы Финна В.К. в своей работе «Об интеллектуальном анализе данных»,[20] а также в работе [8]. Полный разбор идей Финна потребовал бы не одной статьи, поэтому ограничимся краткой выжимкой.
Одной из самых важных, на взгляд автора гипотез, является предложенная им логическая абстракция, которую можно было бы назвать структурной моделью любой автоматизированной интеллектуальной системой:
АИИС=(РИС+ПИС+ИНИН)+ПАП,
где:
АИИС – автоматизированная интеллектуальная информационная система,
РИС =(генератор гепотиз+доказатель теорем+вычислитель), Финн В.К. назвал его «Рассуждатель»,
ПИС – поисково-информационная система,
ИНИП – интеллектуальный интерфейс (диалог, графика, обучение пользователя работе с системой)
ПАП – подсистема автоматического пополнения БД из «информационной среды».
АИИС в свою очередь имеет два блока: базу данных-фактов (БД) и базу знаний (БЗ). База данных состоит из объектов с заданной структурой: конечные множества, кортежи, слова, графы и т.д… База знаний состоит: из аксиом, задающих структуру данных (например, из аксиом булевой алгебры, алгебры кортежей…), аксиом связи исходных (для БД) предикатов, которые неявно задают класс решаемых задач (например, задачи распознавания причинных зависимостей).
Для полноценной реализации полного ИИ по Серлу недостает понимания где должен размещаться такие подсистемы как сознание и вытекающие из этого функции по определению целей существования системы или то, что мы называем «любопытством», где заложить «глубину ума». Без этого невозможна самостоятельная постановка задачи системой. Надо отдать должное Финну, в своих работах он обращает на это внимание, но в рамках данной абстракции не посчитал нужным выделить эти вопросы в отдельный функциональный блок.
Анализируя компоненты, встает вопрос о необходимости решения огромного спектра математических и аналитических задач. С генерацией гипотез или дедукции все не так плохо, по крайней мере есть вполне рабочие гипотезы. Но вот что касается философско-математических вопросов индукции, абдукции пока полная неясность. Как работать с предикатами высших порядков? Какова общая структура аксиом? Как решать вопросы оперирования предикатов более чем двух трех порядков? Создавать язык программирования или оперировать чем-то похожим на графы и многомерные массивы? Нет понятной математики для работы с ассоциативными полями. Как анализировать конкуренцию выводов в рамках многомерности пространства как ассоциативных связей, так многомерности пространства возможных выводов? Ведь в каждом из «возможных миров» будет правильным свой вывод… Какова логика и математика проблем вывода количества и качества? Это только незначительная часть вопросов, решение которых еще впереди.
Как и любая научная гипотеза, схема, предложенная Финном не является чем то окончательным. Но на сегодняшний день это, пожалуй, одна из наиболее рабочих гипотез. Анализ каждого из элементов схемы сам по себе достоен отдельной статьи.
Исследования в области реализации каждого из компонентов, создания высокоэффективной шины обмена данными между этими компонентами могут быть довольно перспективными и увлекательными задачами. В условиях бурного роста SaaS, облачных вычислений создание такого рода систем, построенных путем интеграции компонентов от разных команд, могли бы дать значительный прорыв в данном вопросе. Созданные на таком принципе Интеллектуальные агенты, могли бы действительно научится решать гораздо больший класс задач.
Последнее замечание, которое хотелось бы сделать касается самого термина «Искусственный интеллект». Было бы справедливым понимать термин ИИ как общее и, скорее, философское понятие. В рамках же практических задач более уместным было бы использование термина «Интеллектуальный агент». Этот термин мог бы дать более четкое понимание ограниченности решения с точки зрения объемов информации, используемых логик, спектров решаемых задач и целеполагания создаваемых систем. Употребление слова «ограниченность» следует понимать не как ущербность, а как понимание границ возможностей и избежать возможной подмены понятий.
Решение же самих по себе задач ML, создание тензорных процессоров является в лучшем случае не более чем копанием в рамках одного из компонентов модели Финна.
В настоящее время не решена ни одна из проблем логического вывода (дедукция-индукция-абдукция) кроме частичного решения вопросов связанных с дедуктивными выводами. С точки зрения полного ИИ не решена вообще не одна задача. Основная проблема заключается в том, что подавляющее большинство исследований не затрагивают реализацию самой абстракции, хотя бы в понимании Финна, а следовательно носят тупиковый с точки зрения ИИ-полной реализации характер.
В итоге все основные, из известных на данный момент автору этой статьи, направления мысли представляют собой в терминах Финна В.К. не более чем игры вокруг базы фактов и практически никак не оперируют базами знаний, представляющих собой абстракции как результаты абдукции.
Так же как по меткому выражению Майкла Джордано о том, что «чрезмерное использование больших данных, вероятно, приведет к катастрофам в сфере анализа, сопоставимым с массовым обрушением мостов», все то же самое скорее всего произойдет и с сегодняшними усилиями в области ИИ.
Все вышесказанное не является утверждением бесперспективности нейронных сетей или аналогичных технологий. Объем задач и их ценность огромны. Это и помощь в распознавании образов и помощь специалистам в разных областях при анализе данных и незначительных на первый взгляд деталей. Хорошим примером такого применения является помощь ИИ в установке диагнозов.
Рождение современной математики, конечно же, процесс долгий, затянувшийся на века. Наблюдая современные тенденции, напрашивается неутешительный вывод: все движется по кругу. Философы древней Греции не знали математики и математических формул, оперировали понятиями на уровне образов и «бытовых» понятий. Этого становилось недостаточно для организации более сложных и, самое главное, абстрактных рассуждений, что и привело к рождению математики в ее современном понимании. Современные рассуждения и логика того, что называют «искусственным интеллектом» сегодня проходят тот же путь. И состояние сегодняшнего дня «уводит» обратно к истокам, так как в большей степени базируется на тех же принципах поиска «общих» закономерностей скорее в стиле Пифагора и Евклида.
Одной из основных задач математики является поиск логик, позволяющих значительно снизить затраты на расчеты путем вывода компактных и оптимальных закономерностей. Все это послужило толчком для создания сегодняшней математики с ее современными нотациями. Начало же просматривается не ранее XVI века целым рядом ученых таких как Декарт, Лейбниц и т.д. С точки зрения ИИ – мы пока не достигли даже XVII века.
Рождение математики, способной к индукции и абдукции еще впереди, а взрывной рост интереса к ИИ в основном связан ростом вычислительных возможностей, а не возникновениям новых алгоритмов. Но в результате этого роста все же была достигнута точка, после которой решение большого как по сферам применения, так и исходных данных, но относительно небольшого по аналитической сложности объема задач стала экономически целесообразной. Но это все же экстенсивный путь развития.
Без решения логико-философских вопросов, без создания новых областей математики, в частности, дальнейшее движение не представляется возможным.