в чем заключается метод случайных подпространств в композициях моделей машинного обучения

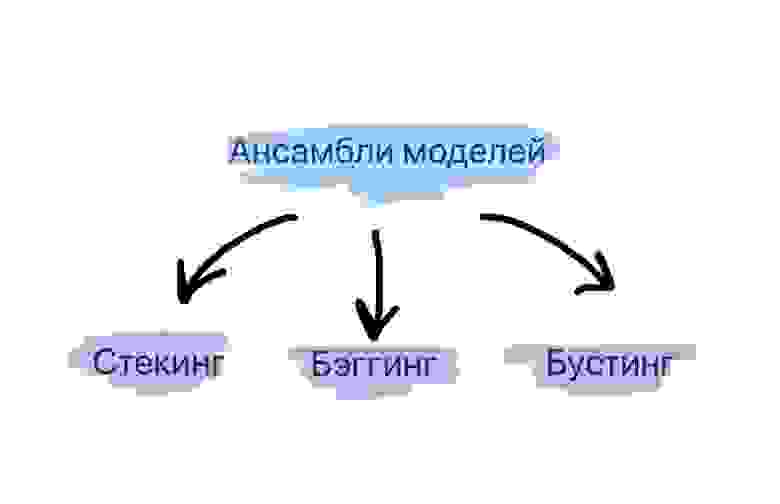
Методы сбора ансамблей алгоритмов машинного обучения: стекинг, бэггинг, бустинг

Что такое ансамбли моделей?

Стекинг. Могут рассматриваться разнородные отдельно взятые модели. Существует мета-модель, которой на вход подаются базовые модели, а выходом является итоговый прогноз.

Бэггинг. Рассматриваются однородные модели, которые обучаются независимо и параллельно, а затем их результаты просто усредняются. Ярким представителем данного метода является случайный лес.

Бустинг. Рассматриваются однородные модели, которые обучаются последовательно, причем последующая модель должна исправлять ошибки предыдущей. Конечно, в качестве примера здесь сразу приходит на ум градиентный бустинг.

Рисунок 1

Три этих способа и будут детальнее рассмотрены далее.

Стекинг

Из трех вариантов стекинг является наименее популярным. Это можно проследить и по числу готовых реализаций данного метода в программных библиотеках. В том же sklearn.ensemble в python куда чаше используют AdaBoost, Bagging, GradientBoosting, чем тот же самый Stacking (хотя его реализация там тоже есть).

Стекинг выделяется двумя основными чертами: он может объединить в себе алгоритмы разной природы в качестве базовых. Например, взять метод опорных векторов (SVM), k-ближайших соседей (KNN) в качестве базовых и на основе их результатов обучить логистическую регрессию для классификации. Также стоит отметить непредсказуемость работы метамодели. Если в случае бэггинга и бустинга существует достаточно четкий и конкретный ансамблевый алгоритм (увидим далее), то здесь метамодель может с течением времени по-разному обучаться на входных данных.

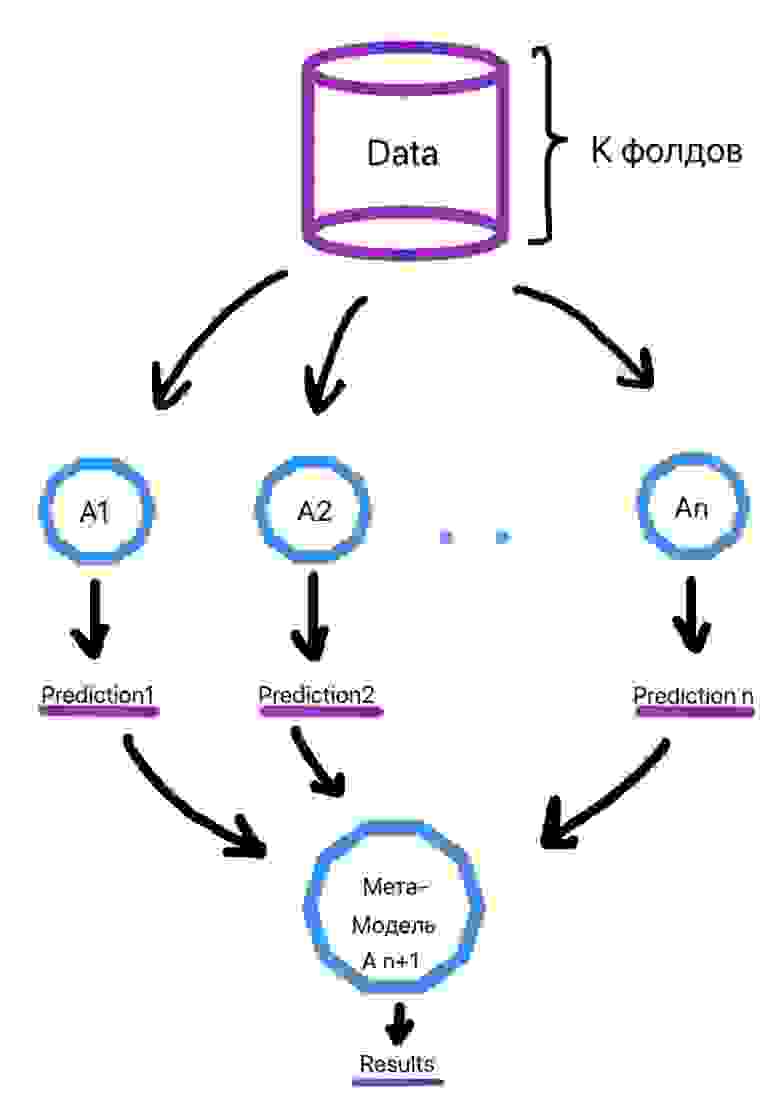
Алгоритм обучения выглядит следующим образом (рис. 2):

Делим выборку на k фолдов (тот же смысл, что и в кросс-валидации).

Для объекта из выборки, который находится в k-ом фолде, делается предсказание слабыми алгоритмами, которые были обучены на k-1 фолдах. Этот процесс итеративен и происходит для каждого фолда.

Создается набор прогнозов слабых алгоритмов для каждого объекта выборки.

На сформированных низкоуровневыми алгоритмами прогнозах в итоге обучается метамодель.

Рисунок 2

Ссылки на библиотеки для использования метода приведены ниже:

Бэггинг

Бэггинг является уже более популярным подходом и зачастую при упоминании этого термина вспоминается алгоритм построения случайного леса, как наиболее типичного его представителя.

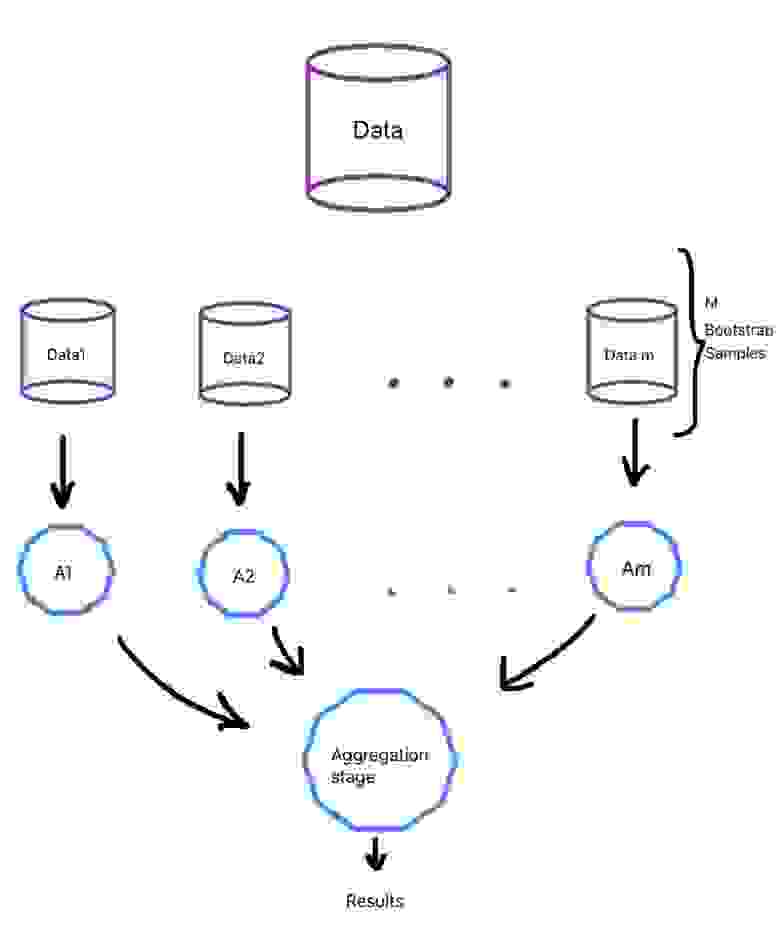
При данном методе базовые алгоритмы являются представителями одного и того же семейства, они обучаются параллельно и почти независимо друг от друга, а финальные результаты лишь агрегируются. Нам необходимо, чтобы на вход слабым алгоритмам подавались разные данные, а не один и тот же набор, ведь тогда результат базовых моделей будет идентичен и смысла в них не будет.

0.632*n разных объектов. Таким образом, должны сформироваться m обучающих выборок для m слабых алгоритмов.

Бутстрэп выборки являются в значительной степени независимыми. Отчасти поэтому и говорят, что базовые алгоритмы обучаются на выборках независимо.

Что касается агрегации выходов базовых алгоритмов, то в случае задачи классификации зачастую просто выбирается наиболее часто встречающийся класс, а в случае задачи регрессии выходы алгоритмов усредняются (рис. 3). В формуле под ai подразумеваются выходы базовых алгоритмов.

Рисунок 3

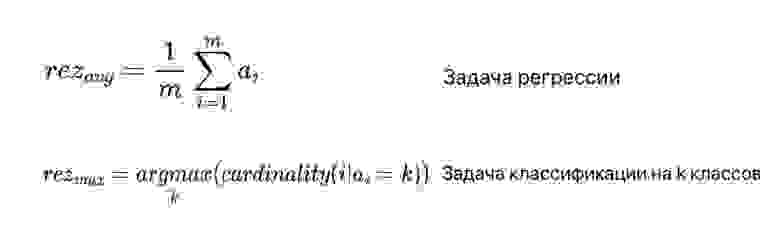
Общий процесс приведен на рисунке ниже (рис. 4):

Рисунок 4

Случайный лес

Рисунок 5

Ссылки на библиотеки для использования метода приведены ниже:

Бустинг

В данном случае, модели уже не обучаются отдельно друг от друга, а каждая следующая правит ошибки предыдущей. То есть можно сказать, что если один слабый алгоритм не смог выявить какую-либо закономерность в данных, так как это было для него сложно, то следующая модель должна сделать это. Но из данного подхода вытекает недостаток: работу алгоритма трудно распараллелить из-за зависимости предыдущего и последующего шагов.

Бустинг направлен скорее на уменьшение смещения в данных, чем на снижение разброса в них. Поэтому в качестве базовых алгоритмов могут браться модели с достаточно высоким смещением, например, неглубокие случайные деревья.

Рисунок 6

Типичными представителями бустинга являются две модели: градиентный бустинг и AdaBoost. Обе по-разному решают одну и ту же оптимизационную задачу по поиску итоговой модели, представляющей собой взвешенную сумму слабых алгоритмов (рис. 6).

Градиентный бустинг использует типичный алгоритм градиентного спуска для решения задачи. Когда приходит время добавить новый слабый алгоритм в ансамбль делается следующее:

Находится оптимальный вектор сдвига, улучшающий предыдущий ансамбль алгоритмов.

Этот вектор сдвига является антиградиентом от функции ошибок работы предыдущего ансамбля моделей

Благодаря вектору сдвигов мы знаем, какие значения должны принимать объекты обучающей выборки

А поскольку нам надо найти очередной алгоритм в композиции, то находим тот, при использовании которого минимизируется отклонение ответов от истинных

Ссылки на библиотеки для использования метода приведены ниже:

Заключение

Таким образом, мы увидели, что для того, чтобы улучшить качество функционирования отдельно взятых моделей машинного обучения, существует ряд техник их объединения в ансамбли. Эти техники уже заложены в программные продукты и ими можно пользоваться, улучшая свое решение. Однако, с моей точки зрения, при решении задачи не стоит сразу же браться за них. Лучше сначала попробовать одну простую, отдельную модель, понять, как она функционирует на конкретных данных, а уже дальше использовать ансамбли.

Источник

Машинное обучение

Материал из MachineLearning.

Содержание

Машинное обучение (Machine Learning) — обширный подраздел искусственного интеллекта, изучающий методы построения алгоритмов, способных обучаться. Различают два типа обучения. Обучение по прецедентам, или индуктивное обучение, основано на выявлении общих закономерностей по частным эмпирическим данным. Дедуктивное обучение предполагает формализацию знаний экспертов и их перенос в компьютер в виде базы знаний. Дедуктивное обучение принято относить к области экспертных систем, поэтому термины машинное обучение и обучение по прецедентам можно считать синонимами.

Машинное обучение находится на стыке математической статистики, методов оптимизации и классических математических дисциплин, но имеет также и собственную специфику, связанную с проблемами вычислительной эффективности и переобучения. Многие методы индуктивного обучения разрабатывались как альтернатива классическим статистическим подходам. Многие методы тесно связаны с извлечением информации и интеллектуальным анализом данных (Data Mining).

Наиболее теоретические разделы машинного обучения объединены в отдельное направление, теорию вычислительного обучения (Computational Learning Theory, COLT).

Машинное обучение — не только математическая, но и практическая, инженерная дисциплина. Чистая теория, как правило, не приводит сразу к методам и алгоритмам, применимым на практике. Чтобы заставить их хорошо работать, приходится изобретать дополнительные эвристики, компенсирующие несоответствие сделанных в теории предположений условиям реальных задач. Практически ни одно исследование в машинном обучении не обходится без эксперимента на модельных или реальных данных, подтверждающего практическую работоспособность метода.

Общая постановка задачи обучения по прецедентам

Дано конечное множество прецедентов (объектов, ситуаций), по каждому из которых собраны (измерены) некоторые данные. Данные о прецеденте называют также его описанием. Совокупность всех имеющихся описаний прецедентов называется обучающей выборкой. Требуется по этим частным данным выявить общие зависимости, закономерности, взаимосвязи, присущие не только этой конкретной выборке, но вообще всем прецедентам, в том числе тем, которые ещё не наблюдались. Говорят также о восстановлении зависимостей по эмпирическим данным — этот термин был введён в работах Вапника и Червоненкиса.

Наиболее распространённым способом описания прецедентов является признаковое описание. Фиксируется совокупность n показателей, измеряемых у всех прецедентов. Если все n показателей числовые, то признаковые описания представляют собой числовые векторы размерности n. Возможны и более сложные случаи, когда прецеденты описываются временными рядами или сигналами, изображениями, видеорядами, текстами, попарными отношениями сходства или интенсивности взаимодействия, и т. д.

Для решения задачи обучения по прецедентам в первую очередь фиксируется модель восстанавливаемой зависимости. Затем вводится функционал качества, значение которого показывает, насколько хорошо модель описывает наблюдаемые данные. Алгоритм обучения (learning algorithm) ищет такой набор параметров модели, при котором функционал качества на заданной обучающей выборке принимает оптимальное значение. Процесс настройки (fitting) модели по выборке данных в большинстве случаев сводится к применению численных методов оптимизации.

Замечание о терминологии. В зарубежных публикациях термин algorithm употребляется только в указанном выше смысле, то есть это вычислительная процедура, которая по обучающей выборке производит настройку модели. Выходом алгоритма обучения является функция, аппроксимирующая неизвестную (восстанавливаемую) зависимость. В задачах классификации аппроксимирующую функцию принято называть классификатором (classifier), концептом (concept) или гипотезой (hypothesys); в задачах восстановления регрессии — функцией регрессии; иногда просто функцией. В русскоязычной литературе аппроксимирующую функцию также называют алгоритмом, подчёркивая, что и она должна допускать эффективную компьютерную реализацию.

Типология задач обучения по прецедентам

Основные стандартные типы задач

Специфические прикладные задачи

Некоторые задачи, возникающие в прикладных областях, имеют черты сразу нескольких стандартных типов задач обучения, поэтому их трудно однозначно отнести к какому-то одному типу.

Приложения

Целью машинного обучения является частичная или полная автоматизация решения сложных профессиональных задач в самых разных областях человеческой деятельности. Машинное обучение имеет широкий спектр приложений:

Сфера применений машинного обучения постоянно расширяется. Повсеместная информатизация приводит к накоплению огромных объёмов данных в науке, производстве, бизнесе, транспорте, здравоохранении. Возникающие при этом задачи прогнозирования, управления и принятия решений часто сводятся к обучению по прецедентам. Раньше, когда таких данных не было, эти задачи либо вообще не ставились, либо решались совершенно другими методами.

Подходы и методы

Подход к задачам обучения — это концепция, парадигма, точка зрения на процесс обучения, приводящая к набору базовых предположений, гипотез, эвристик, на основе которых строится модель, функционал качества и методы его оптимизации.

Разделение методов «по подходам» довольно условно. Разные подходы могут приводить к одной и той же модели, но разным методам её обучения. В некоторых случаях эти методы отличаются очень сильно, в других — совсем немного и «плавно трансформируются» друг в друга путём незначительных модификаций.

Статистическая классификация

В статистике решение задач классификации принято называть дискриминантным анализом.

Байесовская теория классификации основана на применении оптимального байесовского классификатора и оценивании плотностей распределения классов по обучающей выборке. Различные методы оценивания плотности порождают большое разнообразие байесовских классификаторов. Среди них можно выделить три группы методов:

Параметрическое оценивание плотности

Непараметрическое оценивание плотности

Оценивание плотности как смеси параметрических плотностей

Несколько особняком стоит наивный байесовский классификатор, который может быть как параметрическим, так и непараметрическим. Он основан на нереалистичном предположении о статистической независимости признаков. Благодаря этому метод чрезвычайно прост.

Другие теоретико-вероятностные и статистические подходы:

Классификация на основе сходства

Метрические алгоритмы классификации применяются в тех задачах, где удаётся естественным образом задавать объекты не их признаковыми описаниями, а матрицей попарных расстояний между объектами. Классификация объектов по их сходству основана на гипотезе компактности, которая гласит, что в «хорошей задаче» схожие объекты чаще лежат в одном классе, чем в разных.

Метрические алгоритмы относятся к методам рассуждения на основе прецедентов (Case Based Reasoning, CBR>. Здесь действительно можно говорить о «рассуждениях», так как на вопрос «почему объект u был отнесён к классу y?» алгоритм может дать понятный эксперту ответ: «потому, что имеются прецеденты — схожие с

ним объекты, принадлежащие классу y», и

предъявить список этих прецедентов.

Наиболее известные метрические алгоритмы классификации:

Классификация на основе разделимости

Большая группа методов классификации основана на явном построении разделяющей поверхности в пространстве объектов. Из них чаще всех применяются Линейные классификаторы:

Нейронные сети

Нейронные сети основаны на принципе коннективизма — в них соединяется большое количество относительно простых элементов, а обучение сводится к построению оптимальной структуры связей и настройке параметров связей.

Индукция правил (поиск закономерностей)

Категория:Логические алгоритмы классификации представляют собой композиции простых, легко интерпретируемых правил.

Кластеризация

Регрессия

Алгоритмические композиции

Сокращение размерности

Выбор модели

Байесовский вывод

На середину 2016 года лидирующие позиции в мире статистической обработки информации занимает R, который, в частности, содержит обширный набор пакетов для машинного обучения.

Нейронные сети: нейронная сеть с одним скрытым слоем реализована в пакете nnet (поставляется в составе R). Пакет RSNNS предлагает интерфейс к Stuttgart Neural Network Simulator (SNNS). Интерфейс к библиотеке FCNN позволяет расширяемые пользователем искусственные нейронные сети в пакете FCNN4R.

Рекурсивное разделение: модели с древовидной структурой для регрессии, классификации и анализа дожития, следующие идеям в документации CART, реализованы в пакетах rpart и tree (поставляется с R). Пакет rpart рекомендуется для вычислений подобных CART-деревьям. Обширный набор инструментов алгоритмов разделения доступен в пакете Weka, RWeka обеспечивает интерфейс этой реализации, включая J4.8-вариант C4.5 и M5. Кубиxческий пакет подгоняет модели, основанными на правилах (подобными деревьям) с линейными регрессионными моделями в терминальных листах, основанных на коррекции наблюдений и бустинге. Пакет C50 может подогнать деревья классификации C5.0, модели, основанные на правилах и их версиях бустинга.

Два рекурсивных алгоритма разделения с несмещенным выбором переменной и статистическим критерием остановки реализованы в пакете party. Функция ctree () основывается на непараметрических условных процедурах вывода для тестирования независимости между откликом и каждой входной переменной, тогда как mob() может использоваться, чтобы разделить параметрические модели. Расширяемые инструменты для визуализации двоичных деревьев и распределений узла отклика также доступны в пакете party.

Модели древовидной структуры с изменяемыми коэффициентами реализованы в пакете vcrpart.

Для задач с двоичными входными переменными пакет LogicReg реализует логистическую регрессию. Графические инструменты для визуализации деревьев доступны в пакете maptree.

Деревья для моделирования длящихся данных посредством случайных эффектов предлагаются пакетом REEMtree. Разделение смешанных моделей выполнено RPMM. Вычислительная инфраструктура для представления деревьев и объединенных методов для предсказания и визуализации реализована в partykit. Эта инфраструктура используется пакетом evtree, чтобы реализовать эволюционное приобретение знаний о глобально оптимальных деревьях. Наклонные деревья доступны в пакете oblique.tree.

Бустинг (усиление): различные формы градиентного бустингаа реализованы в пакете gbm (бустинг, основанный на дереве функциональный градиентный спуск). Оптимизируется функция потерь Hinge с помощью бустинга, реализованного в пакете bst. Можно использовать пакет GAMBoost для подгонки обобщенных аддитивных моделей алгоритмом бустинга. Расширяемая платформа бустинга для обобщенных линейных, аддитивных и непараметрических моделей доступна в пакете mboost. Основанный на правдоподобии бустинг для моделей Cox реализовано в CoxBoost и для смешанных моделей в GMMBoost. Можно подогнать модели GAMLSS, используя бустинг gamboostLSS.

Методы опорных векторов и ядерные методы: функция svm () из e1071 предлагает интерфейс библиотеке LIBSVM, и пакет kernlab реализует гибкую платформу для ядерного обучения (включая SVMs, RVMs и другие алгоритмы ядерного обучения). Интерфейс к реализации SVMlight (только для one-all классификации) дан в пакете klaR. Соответствующая размерность в пространствах признаков ядра может быть оценена, используя rdetools, который также предлагает процедуры для выбора модели и предсказание.

Байесовские Методы: Bayesian Additive Regression Trees (BART), где заключительная модель определена с точки зрения суммы по многим слабым ученикам (мало чем отличающийся от методов ансамбля), реализованы в пакете BayesTree. Байесовская нестационарная, полупараметрическая нелинейная регрессия и проектирование с помощью древовидного Гауссовского процесса, включая Байесовский CART и древовидной линейные модели, доступны в пакете tgp.

Оптимизация с использованием генетических алгоритмов: Пакеты rgp и rgenoud предлагают подпрограммы оптимизации на основе генетических алгоритмов. Пакет Rmalschains реализует имитационные алгоритмы с цепочками локального поиска, которые являются специальным типом эволюционных алгоритмов, комбинируя генетический алгоритм устойчивого состояния с локальным поиском для реально оцененной параметрической оптимизации.

Правила ассоциации: Пакет arules обеспечивает обе структуры данных для эффективной обработки прореженных двоичных данных, а также интерфейсов к реализациям Apriori, и Eclat для интеллектуальной обработки частотных наборов элементов, максимальных частотных наборов элементов, замкнутых частотных наборов элементов и правила ассоциации.

Системы, основанные на нечетких правилах: пакет frbs реализует стандартные методы для изучения систем, основанных на нечетких правилах для регрессии и классификации. Пакет RoughSets содержит всесторонние реализации грубой теории множеств (RST) и нечеткой грубой теории множеств (FRST) в одном пакете.

Выбор и проверка модели: пакет e1071 содержит функцию настройки tune() для настройки параметров, а функция errorest () (ipred) может использоваться для оценки коэффициента ошибок. Параметр стоимости C для методов опорных векторов может быть выбран, использовав функциональность пакета svmpath. Функции для анализа ROC и другие методы визуализации для сравнения классификаторов доступны в пакете ROCR. Пакеты hdi и stabs реализуют выбор устойчивости для диапазона моделей, hdi также предлагает другие процедуры вывода в высоко-размерных моделях.

Другие процедуры: очевидные классификаторы определяют количество неопределенности по поводу класса тестовых образцов, используя функцию mass Dempster-Shafer в пакете evclass. Пакет OneR (Одно Правило) предлагает алгоритм классификации с улучшениями для сложной обработки отсутствующих значений и числовых данных вместе с обширными диагностическими функциями

Пакеты-обертки: пакет caret содержит функции для подгонки моделей с последующим предсказанием, включая настройку параметров и и мер значимости переменных. Пакет может использовать с различными инструментами по организации параллельных вычислений (например, MPI, NWS и т.д.). В подобном духе пакет mlr предлагает высокоуровневый интерфейс различным пакетам статистически и машинного обучения. Пакет SuperLearner реализует аналогичный набор инструментов. Пакет h2o реализует платформу машинного обучения общего назначения, у которой есть масштабируемые реализации многих популярных алгоритмов, такие как случайный лес, GBM, GLM (с эластичной сетевой регуляризацией), и глубокое обучение (feedforward многоуровневые сети), среди других.

CORElearn реализует довольно широкий класс машинного обучения.

Конференции

Основные международные конференции — ICML, NIPS, ICPR, COLT.

Международные конференции в странах СНГ — ИОИ.

Основные всероссийские конференции — ММРО, РОАИ.

Источник

Классификация методом линейной дистилляции случайной сети

Доброго времени суток! Меня зовут Глухов Игорь, работаю ad-hoc аналитиком в компании X5 Group и являюсь студентом Университета ИТМО. В данной статье будет предоставлен простой метод решения задачи классификации, основанный на линейных нейронных сетях и дистилляции знаний, конкурирующий по качеству с рядом базовых интерпретируемых моделей, а также с нелинейными сетями.

Введение

Одним из наиболее актуальных вопросов в области машинного обучения является интерпретируемость предоставляемых моделей. Для таких сложных моделей, какими являются ансамбли нескольких методов и глубокие нейронные сети, достаточно проблематично извлечь обоснование принятия решения в случае того или иного предсказания. Все более широкое применение машинного обучения в различных системах реального мира способствует увеличению потребности в четком понимании моделей. Разрабатываются различные методы, направленные на повышение интерпретируемости моделей, однако предлагаемые ими объяснения не до конца честны относительно того, как принимает решение исходная модель.

Вдобавок к этому, компромисс между качеством модели и ее интерпретируемостью, имеет место быть далеко не всегда. В случае, когда данные хорошо структурированы и признаки выразительны, то значительной разницы между качеством ансамблей и качеством линейных моделей нет, соответственно, есть основания отдать предпочтение интерпретируемым моделям

В данной работе представляется Метод Линейной Дистилляции – метод, основанный на линейных нейронных сетях, решающий задачу классификации. Он использует линейную функцию для каждого класса датасета, которые обучены моделировать выход некоторой учительской линейной функции для каждого класса отдельно. После того, как модель обучена, мы можем осуществить классификацию путем определения «новизны» (Novelty Detection), опять же, для каждого класса. Данная модель выучивает монотонные зависимости между признаками и целевой меткой, что делает интерпретацию простой. Подобный метод ранее успешно использовался лишь в применении к задаче обучения с подкреплением.

Алгоритм классификации методом дистилляции случайной линейной нейронной сети

Дистилляция Один-ко-Многим

Метод дистилляции случайной нейронной сети использовался в задаче обучения с подкреплением для разведки в средах с разреженными наградами. В этом случае, дистилляция позволяет агенту определить какие состояния были посещены, а какие нет, и таким образом использовать любопытство для эксплуатации. Пусть – множество наблюдаемых состояний. Предиктором мы будем называть сеть, обученную предсказывать поведение таргетаво время взаимодействия со средой, используя среднеквадратическую ошибкудля обновления весов предиктора. Если разность между предсказанием случайной сети и предсказанием предиктора в некотором состоянии средывелика, то это означает высокий показатель любопытства и выдается большая награда. Это можно рассмотреть как модель обнаружения новизны, обучение которой проходит путем дистилляции случайной нейронной сети. Важным утверждением является то, что предикторможет симулировать поведение таргетаесли их выразительная способность идентична. В данной работе это свойство выполнено путем удаления нелинейностей нейронных сетей и снижения их выразительности до линейной функции.

Рассмотрим задачу классификации с обучающим множеством , где метки объектов это множество, где – количество классов. Таким образом, мы имеем размеченный набор данных, где. Предположим, что классификация выполняется некоторым метрическим классификатором, работающим с представлением объекта в пространстве размерности . Также рассмотрим таргет-функцию, ставящую в соответствие объекты нашего набора данных в пространство той же размерности. Она может быть представлена линейной нейронной сетью или матрицей.

Идея заключается в создании линейных предикторовдля каждого класса , которая будет симулировать поведение таргет-функции для заданного класса. Каждый предиктор обучен каждому объектусоответствующего класса ставить в соответствие представление таргет-функции.

Поскольку все функции из множества функций предикторов и таргет-функция являются линейными, их можно представить в матричном виде. К примеру, может рассматриваться как произведение матриц, где – натуральное число. Во время обучения, метки используются для активации одного из предикторов Процесс обучения использует среднеквадратическую функцию потерь (2.1):

Во время оценивания модели, делается предсказания путем использования расстояния между каждым из выходов предикторови выходом таргет-функции. Финальное предсказание выбирается как .

Важно учесть, что несмотря на тот факт, что все предикторы линейны, их композиция не может быть выражена линейной функцией. Тем не менее, на каждом шаге обучения, учитель и таргет линейны.

Таким образом, мы заменили задачу классификации задачей аппроксимации линейной функции несколькими линейными функциями, связанными с каждым из классов. Данный метод называется Дистилляция Один-ко-Многим.

Дистилляция Многие-к-Одному

В прошлой главе был представлен подход к обучению линейных предикторов на выходах линейной таргет-функции. В этой главе, будет представлено два подхода к выбору этой функции.

Во-первых, будут сформулированы необходиме свойства таргет-функции. Поскольку предикторы симулируют выход таргета на соответствующих классах, когда мы сравниваем их выходы, мы можем точнее отличить один предиктор от другого, если класс сильно не похож на другие. К примеру, если выход таргета для класса 1 сильно отличается от его же выхода для других классов, то обученный предиктор, соответствующий классу 1, будет ближе к тагрету, чем остальные. Это будет возможно, если выходы таргета для каждого класса будут далеки друг от друга.

Один из способов выбрать так, чтобы различным классам в соответствие ставились разные области в пространстве размерности выходного слоя – сделать это напрямую. К примеру, это можно сделать, обновляя параметры таргет-функции используя дистилляцию некоторого учителя.

В нашем случае, есть необычное свойство дистилляции: учитель не обязан обобщать данные. Будет достаточно того, чтобы учительская функция ставила разным классам в соответствие разные области выходного пространства. В отличие от стандартной парадигмы дистилляции, в данном методе учителем будет множество рандомизированных линейных функций . Тогда мы сразу по умолчанию получаем различные выходные представления для каждого класса. Во время обучения, для каждого объекта мы выбираем линейную нейронную сеть из согласно метке объекта , после чего используем выбранное преобразование как таргет для . Обучение производится путем минимизации следующей функции потерь (2.3):

Данный метод называется Дистилляция Многие-к-Одному. Точность предсказаний модели, обученная таким образом, неоптимальна. Одной из причин для этого является тот факт, что распределение, которое возвращают учителя, нелинейно. Поэтому у линейной таргет-функции возникают проблемы с выучиванием данного распределения.

Двунаправленная Дистилляция

В предыдущих главах были предложены модели Дистилляция Один-ко-Многим и Дистилляция Многие-к-Одному. В данной главе эти две идеи комбинируются в метод, называемый Двунаправленная Дистилляция.

После инициализации, наши предикторы идентичны , поэтому на первом шаге мы предобучаем функцию на выходы в манере Дистилляции Многие-к-Одному, после чего дистиллируем знания назад в предикторы в манере Дистилляции Один-ко-Многим.

Процедура обучения представлена на рисунке 1. Во время Двунаправленной Дистилляции, мы переключаемся между моделями Дистилляция Один-ко-Многим и моделью Дистилляция Многие-к-Одному в различных пропорциях, обучая их определенное количество итераций, позволяя всем параметрам быть обновленными несколько раз каждую эпоху. Красным отмечены таргет-функция, представленная линейной нейронной сетью и активированный предиктор, соответствующий поступившему на вход объекту класса 2.

Эксперименты

В данной главе, описываются результаты экспериментов, в которых сравнивались модели Дистилляция Один-ко-Многим и Двунаправленная Дистилляция с такими широкоиспользуемыми моделями, как полносвязный персептрон, логистическая регрессия, решающее дерево.

Все эксперименты проведены в парадигме Few-Shot Learning. Каждой модели подавалось размеченных объектов (называется “shot”) для каждого класса из . В отличие от стандартных Few-Shot моделей, наш метод не предполагает перевода знаний между эпизодами (полученными подмножествами размеченных объектов), что делает его похожим на small-sample learning. Во избежание смещения оценки, связанного с маленьким числом объектов в эпизоде, каждая модель обучалась на 100 независимых прогонах по n эпох, после чего возвращалось среднее значение доли верно классифицированных объектов.

Эксперименты проводились на датасетах MNIST, Fashion-MNIST, OMNIGLOT, SVHN. Дополнительно к перечисленным датасетам изобрежаний, были проведены исследования на двух табличных наборах данных: Customer Churn и Covertype.

MNIST

В результат заносились наилучшие значения метрики, полученные для одной из конфигураций гиперпараметров модели. Результаты сравнения приведены в таблице 1. В каждой ячейке представлено значение доли верно классифицированных объектов. Видно, что с увеличением размера датасета, результат становится все лучше, но уже на датасетах размером в около тысячу объектов обучение значительно замедляется.

Источник