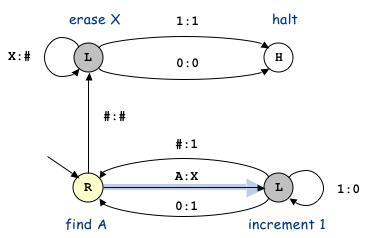
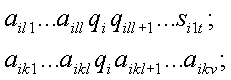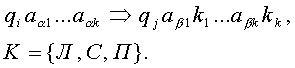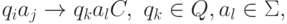В машине тьюринга рабочий алфавит
2.3. Алгоритмическая машина Тьюринга
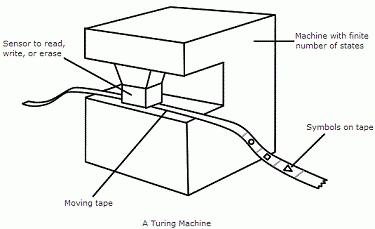
Машина Тьюринга состоит из трех частей: ленты, считывающе-записывающей головки и логического устройства (рис. 2.6).
Рис. 2.6. Схема машины Тьюринга
Головка всегда расположена над одной из ячеек ленты. Работа происходит тактами (шагами). Система исполняемых головкой команд предельно проста: на каждом такте она производит замену знака в обозреваемой ячейке ai знаком aj. При этом возможны сочетания:
Обработка информации и выдача команд на запись знака, а также сдвига ленты в машине Тьюринга производится логическим устройством (ЛУ). Оно может находиться в одном из состояний, которые образуют конечное множество и обозначаются Q = <q1…qm, z>, причем, состояние z соответствует завершению работы, a q1 является начальным (исходным). Q совместно со знаками R, L, S образуют внутренний алфавит машины. ЛУ имеет два входных канала (ai, qi) и три выходных (аi+1, qi+1, Di+1) (см. рис. 2.7):
Рис. 2.7. Изображение логического устройства
Рис. 2.8. Схема функционирования машины Тьюринга
Конкретная машина Тьюринга задается перечислением элементов множеств А и Q, а также, логической функцией, которую реализует ЛУ, т.е. набором правил преобразования. Ясно, что различных множеств A, Q и логических функций может быть бесконечно много, т.е. и машин Тьюринга также бесконечно много.
Совокупность состояний всех ячеек ленты, состояния ЛУ и положение головки называется конфигурацией машины.
Перед началом работы на пустую ленту записывается исходное слово α конечной длины в алфавите А; головка устанавливается над первым символом слова α, ЛУ переводится в состояние q1 (т.е. начальная конфигурация имеет вид q1α). Поскольку в каждой конфигурации реализуется только одно правило преобразования, начальная конфигурация однозначно определяет всю последующую работу машины, т.е. всю последовательность конфигураций вплоть до прекращения работы.
В зависимости от начальной конфигурации возможны два варианта развития событий:
Рис. 2.9. Логическая функция
Пусть начальной является конфигурация 1q1111*. Тогда работа машины в соответствии с описанной логической функции будет происходить следующим образом:
Такт 1 Обозревается 1, в ЛУ состояние q. Выходная команда q1R, что эквивалентно перемещению головки по отношению ленты на 1 шаг вправо. Следовательно, образуется промежуточная конфигурация 11 q111.
* Как указывалось выше, незначащие пустые секции слева и справа от заполненных в конфигурацию не включаются; поскольку в данной задаче несколько заполненных секций следуют подряд, только они и указываются в конфигурации.
Имеется запись многоразрядного целого числа п в десятичной системе счисления; построить машину Тьюринга, которая обеспечивала бы вычисление значение n + 1.
Рис. 2.10. Функциональная схема
Пусть начальной конфигурацией будет 21 q9.
Такт 2 q1→z2S, т.е. 1 будет заменена на 2 и произойдет остановка с конечной конфигурацией 2z20, т.е. получен результат сложения 219 + 1.
Пусть начальной будет конфигурация 99q9.
Такт 1 q9→q0L, т.е. сформируется промежуточная конфигурация 9q90.
Такт 2 q9→ q0L — возникнет конфигурация q900.
Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине Тьюринга.
Эта гипотеза получила название тезиса Тьюринга. Как и тезис Черча, ее нельзя доказать, так как она связывает нестрогое определение понятия алгоритма со строгим определением машины Тьюринга.
В принципе, эта гипотеза может быть опровергнута, если удастся привести пример алгоритма, который не может быть реализован с помощью тьюринговой функциональной схемы. Однако все известные до сих пор алгоритмы могут быть заданы посредством тьюринговых функциональных схем.
Машина Тьюринга
В 1936 г. Аланом Тьюрингом для уточнения понятия алгоритма был предложен абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга.
Кроме того, предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи.
Что собой представляет машина Тьюринга?
Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (головки), которая управляется программой.
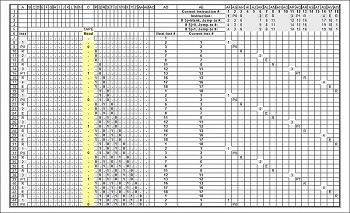
Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.
Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:
Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:
Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния).
Пример работы машины Тьюринга
Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):
Здесь происходит сдвиг головки влево до тех пор, пока она не окажется над пустым символом. После этого машина переходит в состояние q2 (команды которого совпадают с командами q1 предыдущей программы).
В машине тьюринга рабочий алфавит
Отметим, что наличие разнообразных символов в рабочем алфавите МТ позволяет представлять на ленте произвольную текстовую и числовую информацию, а переходы управляющего центра МТ в различные состояния моделируют запоминание машиной Тьюринга промежуточных результатов работы. Таблица, определяющая порядок работы МТ, не является в прямом смысле слова программой (ее предписания выполняются не последовательно, одно за другим, а описывают преобразования символов некоторого текста, находящегося на ленте). Таблицу МТ часто называют схемой машины Тьюринга или попросту отождествляют с самой машиной Тьюринга, коль скоро ее устройство и принцип функционирования известны.
Рассмотрим примеры нескольких схем машины Тьюринга.
1. Алгоритм прибавления единицы к числу в десятичной системе счисления.
Дана десятичная запись числа n (т.е. представление натурального числа n в десятичной системе счисления). Требуется получить десятичную запись числа n +1.
Очевидно, что внешний алфавит МТ должен состоять из десяти цифр 1 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и символа пробела _. Эти цифры записывают по одной в ячейке (подряд, без пропусков).
| a i | q i | |
|---|---|---|
| q 1 | q 2 | |
| 0 | 0 П q 1 | 1 C q 2 |
| 1 | 1 П q 1 | 2 C q 2 |
| 2 | 2 П q 1 | 3 C q 2 |
| 3 | 3 П q 1 | 4 C q 2 |
| 4 | 4 П q 1 | 5 C q 2 |
| 5 | 5 П q 1 | 6 C q 2 |
| 6 | 6 П q 1 | 7 C q 2 |
| 7 | 7 П q 1 | 8 C q 2 |
| 8 | 8 П q 1 | 9 C q 2 |
| 9 | 9 П q 1 | 0 C q 2 |
| _ | _ Л q 1 | 1 C q 2 |
2. Алгоритм записи числа в десятичной системе счисления.
Дана конечная последовательность меток, записанных в клетки ленты подряд, без пропусков. Требуется записать в десятичной системе число этих меток (пересчитать метки).
Легко могут быть построены алгоритмы сложения чисел, их перемножения, нахождения наибольшего общего делителя и т.д. Однако главная цепь введения машин Поста и Тьюринга не программирование для них, а изучение свойств алгоритмов и проблемы алгоритмической разрешимости задач.
В зависимости от числа используемых лент, их назначения и числа состояний устройства управления можно рассматривать различные модификации машин Тьюринга.
первый индекс соответствует моменту времени, второй – номеру ленты, третий – номеру клетки, считая слева направо. Говорят, что машина выполняет команду
Для сравнения структур различных машин и оценки их сложности необходимо иметь соответствующую меру сложности машин. К.Шеннон предложил рассматривать в качестве такой меры произведение числа символов внешнего алфавита и числа внутренних состояний. Большой интерес вызывает задача построения универсальной машины Тьюринга наименьшей сложности.
Алгоритмы: машины Тьюринга
Основные определения
Рассматриваемая в этом разделе модель алгоритмов была предложена английским математиком Тьюрингом в 1937 г. еще до создания современных компьютеров 1 Аналогичная модель вычислений была примерно в то же время определена Е. Постом. Поэтому иногда такие машины называют машинами Тьюринга-Поста Он исходил из общей идеи моделирования работы вычислителя, оперирующего в соответствии с некоторым строгим предписанием. В машине Тьюринга расчленение процесса вычисления на элементарные шаги доведено в известном смысле до предела. Элементарным действием является замена одного символа в ячейке на другой и перемещение к соседней ячейке. При таком подходе процесс вычисления значительно удлиняется, но зато логическая структура процесса сильно упрощается и приобретает удобный для теоретического исследования вид.
включающая следующие компоненты:
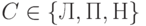
Будем говорить, что некоторый символ стирается, если он заменяется на пустой. Два слова из 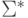


Аналогичное определение можно дать и для других спосбов кодирования чисел (двоичного, десятичного и др.). Ниже мы покажем, что класс вычислимых функций не зависит от выбора одного из таких кодирований.
Машина Тьюринга: описание и примеры машин Тьюринга
Что это и кто создал
Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье «О вычислимых числах с приложением к проблеме разрешимости», которая появилась в Трудах Лондонского математического общества.
Из чего состоит устройство
Каждая такая машина состоит из двух составляющих:
Как работает механизм
Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.
Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.
Свойства механизма
Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:
Функции машины Тьюринга
В решении алгоритмов часто требуется реализация функции. В зависимости от возможности написания цепочки для вычисления, функцию называют алгоритмически разрешимой или неразрешимой. В качестве множества натуральных или рациональных чисел, слов в конечном алфавите N для машины рассматривается последовательность множества В – слова в рамках двоичного кодового алфавита В=<0.1>. Также в результат вычисления учитывается «неопределенное» значение, которое возникает при «зависании» алгоритма. Для реализации функции важно наличие формального языка в конечном алфавите и решаемость задачи распознавания корректных описаний.
Программа для устройства
Составляющие для вычислений
Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.
Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.
Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.
Алгоритм для автомата
Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:
Машина Тьюринга: примеры
Пример 1. Дана задача построить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.
Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:
| a0 | 0 | 1 | 2 | 3 | . | 7 | 8 | 9 | |
| q1 | 1 H q0 | 1 H q0 | 2 H q0 | 3 H q0 | 4 H q0 | . | 8 H q0 | 9 H q0 | 0 λ q1 |
Здесь q1 — состояние изменения цифры, q0 — остановка. Если в q1 автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q0, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q1. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q0 – остановка.
| a0 | ( | ) | |
| q1 | a0 H q0 | ( П q2 | ) П q1 |
| q2 | a0 H q0 | ( П q2 | ) λ q3 |
| q3 | a0 H q0 | a0 П q3 | a0 П q1 |
Состояние q1: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q2; если определен “a0”, то остановка.
Состояние q2: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q3.
Состояние q3: осуществить удаление сначала символа “(”, а затем “)” и перейти в q1.