В процессе управления беспилотным автомобилем bicycle model описывает
От процедурной генерации к детерминизму: подходы к моделированию синтетических данных для беспилотных авто
Симуляции очень важны для ускорения развития методов проектирования во многих отраслях промышленности. В области автомобильных систем беспилотной езды симуляции традиционно используются для тестирования алгоритмов планирования и управления движением. Повторные симуляции используются для разработки систем распознавания, в которых данные с датчиков дорожного движения записываются и воспроизводятся с помощью разнообразных программных стеков для проверки эксплуатационных качеств. Впрочем, эти симуляции были преимущественно ограничены сценариями, встречающимися в реальных автомобилях.
Существует и еще один тип симуляции, становящийся все более важным – генерация высококачественных искусственных данных, точно передающих информацию о реальных дорожных ситуациях. Проблема использования исключительно дорожных данных заключается в том, что для приближения к границам возможностей модулей распознавания в различных операционных областях необходимо собрать и разметить огромные массивы данных. Кроме того, алгоритмы распознавания перестают соответствовать имеющимся данным и выходят из строя при работе вне отработанной среды и при других условиях. В свою очередь, синтетические данные могут создаваться быстро и дешево, а их описания создаются автоматически с использованием базовых знаний о моделируемой среде.
Проблемы генерации синтетических данных для модулей восприятия
Несмотря на то, что задача синтетического моделирования данных для датчиков кажется простой и очевидной, на самом деле она очень сложна. Помимо создания реалистичных синтетических сред разных регионов (например, Сан-Франциско или Токио), для моделирования каждого типа датчика требуется детальное знание основных физических свойств и особенностей различных датчиков, используемых в отрасли. Также, несмотря на то, что для других приложений моделирование может выполняться значительно медленнее, чем в реальном времени, большинству алгоритмов беспилотной езды требуется именно производительность, приближенная к работе в режиме реального времени. Таким образом, в разных сценариях использования необходимы разные уровни производительности и точности моделирования.
Несмотря на то, что для моделирования каждого из датчиков прикладываются значительные усилия, специалисты ожидают, что в ближайшее время между реальными и синтетическими данными возникнет ощутимый разрыв. Алгоритмы восприятия могут обучаться на реальных данных с датчиков и тестироваться на синтетических данных (переход от реальных данных к синтетическим) и наоборот (переход от синтетических данных к реальным), причем алгоритмы разных видов будут работать по-разному. Данная проблема относится не только к данным для симуляций. Алгоритмы восприятия с определенным набором датчиков, обученные на дорогах Калифорнии, скорее всего будут работать хуже с другим набором датчиков. Также этот алгоритм может плохо работать при тестировании на дорогах в других регионах.
Рис. 1: тестирование систем восприятия на синтетических данных
Создание трехмерных синтетических сред
Многие подходы к созданию окружающих сред были разработаны в результате десятилетий работы индустрии развлечений. Впрочем, между отраслями беспилотного транспорта и развлечений существуют значительные отличия. Несмотря на то, что в обеих сферах присутствуют высокие требования к фотореализму, к средам для беспилотного транспорта есть дополнительные требования: они должны создаваться дешево и быстро (в то время как в индустрии развлечений на это могут уходить месяцы), должны быть чрезвычайно реалистичными (как для человеческого глаза, так и для датчиков) и вариативными, а также должны поддерживать множество тестовых случаев.
Обычно трехмерные среды создаются вручную – 3D-художник создает ресурсы и размещает их в создаваемом мире. Такой подход дает фотореалистичные результаты и отлично подходит для демонстраций. Впрочем, из-за своего ручного характера, он не масштабируется для создания виртуальных областей со всего земного шара и не позволяет создать столько виртуальных сред, сколько требуется для тестирования беспилотного транспорта. Таким образом, мы сталкиваемся с ограничениями виртуальных сред.
Альтернативный подход заключается в использовании методов сканирования реального мира – он гарантирует соответствие искусственной среды с ее образцом. Недостаток этого метода заключается в том, что данные реального мира зачастую имеют множество погрешностей и неточностей. Поскольку освещение запечено, а по поверхности невозможно определить ее материал, камеры и лидары выдают лишь приближенные данные. Кроме того, в среде могут встречаться разрывы, неправильные описания и движущиеся объекты, которые необходимо удалить. Также этот метод выдвигает значительные требования к ресурсам для хранения данных и вычислений, а также он может моделировать только те области, которые встречаются в реальной жизни.
Относительно новых подход – создание виртуальных миров на основе процедурной генерации. Таким образом можно быстро создавать большие области и города на основе разнообразных входных данных, в результате чего мир будет создаваться с помощью математических методов (рис. 2). Также этот подход позволяет указывать множество различных вариантов среды, чтобы предотвратить переобучение. Такие параметры, как время дня или погода могут быть изменены при условии точности аннотаций. В целом, новые карты могут создаваться за малые доли того времени, которое требуется для ручного создания виртуальных сред. Сложность этого подхода заключается в обеспечении качественного создания объектов реального мира без ручных правок.
Рис. 2: процедурно сгенерированные здания в высоком разрешении
Точное моделирование датчиков
При генерации синтетических данных в качестве входных данных для датчиков используются среды, о которых мы говорили выше. Эти датчики должны быть способны симулировать оценку глубины лидаром, характеристики цифрового формирования луча радаром и источники шумов в камерах. При этом, эти датчики должны быть достаточно производительными, чтобы осуществлять программно-аппаратное тестирование или работать с приложениями машинного обучения, требующими большие объемы данных.
Несмотря на то, что предположение о том, что датчик может работать с сотнями и тысячами разновидностей условий и топологий, в конечном итоге все они должны подчиняться одним и тем же фундаментальным принципам передачи энергии и теории информации. Тщательно продуманная структура симуляции датчиков может обеспечить гибкость структуры, используемой в различных условиях. Эта основополагающая философия основывается на стремлении перенести инструменты для разработки электрооптических систем и систем обработки сигналов из мира проектирования датчиков в мир симуляции и технологий восприятия.
Даже если система хорошо продумана с теоретической точки зрения, она ценна лишь настолько, насколько она может улавливать свойства своего аналога из реального мира. Степень корреляции между реальностью и моделью сильно зависит от сценариев использования. В простых сценариях может быть достаточно простой сводной таблицы с данными, в то время как в других случаях может потребоваться количественная статистическая оценка различных свойств и характеристик – для этого как правило используют сочетание лабораторных и полевых экспериментов для определения конкретных свойств датчика. Таким образом, моделирование работы датчиков (и точность этого моделирования) можно рассматривать как науку, в которой берется эталон, который затем последовательно ухудшается.
Рис. 3: симуляция вращающегося лидара с 128 лазерами
Эффективность и повторяемость синтетических данных
Существует два аспекта, которые ограничивают удобство использования синтетических данных – эффективность и повторяемость. Ввиду множества причин, самая большая проблема при моделировании датчиков для систем беспилотной езды – это точность, которая может быть достигнута в рамках требований к обработке в реальном времени. Точность и производительность также тесно связаны с масштабируемостью поколений синтетических датчиков. Для создания масштабируемого решения все более важным становится параллельное использование ресурсов.
Такая координация ресурсов естественным образом подводит нас к вопросу о повторяемости. Для того, чтобы распараллеливание приносило пользу, необходимо обеспечить баланс между параллельным и непараллельным моделированием. Детерминизм — это ключевой компонент, который позволяет инженерам тестировать изменения в своих алгоритмах изолированно, в то же время используя разнообразные возможности моделирования.
Симуляция датчиков: адаптация к частным случаям
После того как будут созданы методы разработки сред и датчиков, возникнет следующий вопрос – достаточно ли получаемых синтетических данных для всех сценариев использования? Сценарии использования могут варьироваться в зависимости от степени готовности программного обеспечения: от проверки размещения датчиков с использованием синтетических данных до тестирования финальных версий производственных систем перед их развертыванием.
У всех сценариев использования имеются разные требования к уровням точности модели. Эти уровни точности управляют процессами проверки и валидации. Проверка описывает процесс определения соответствия получившейся модели и исходной спецификации (удалось ли нам создать то, что мы изначально планировали?). Также проверка связана с определением детерминизма (воспроизводятся ли результаты модели каждый раз в одних и тех же условиях?) При валидации же все наоборот: для определения соответствия модели потребностям целевого приложения учитываются требования конечного пользователя. В некоторых случаях допустимо даже использование грубого приближения к физической модели, лежащей в основе датчика. Впрочем, в сценариях использования для производственных испытаний требуются синтетические модели датчиков, которые прошли испытания как лабораторных условиях, так и в реальных – это необходимо для обеспечения точного соответствия допустимым уровням неопределенности.
Задача оценки моделей датчиков также более сложна, чем простая проверка уровня выходного сигнала. Несмотря на то, что это справедливо для многих технологий восприятия в системах беспилотной езды, конечный пользователь также заинтересован в том, чтобы модели восприятия работали эффективно как на синтетических данных, так и на реальных. Эти модели могут быть основаны на компьютерном зрении или построены с использованием различных методик машинного и глубокого обучения. В этих сценариях использования источники неопределенности неизвестны (в случае, если к модели датчика нет полного доверия).
Подход Applied Intuition
Компания Applied Intuition с нуля разработала инструмент для моделирования систем восприятия, который позволяет решать проблемы, описанные выше. Этот инструмент включает в себя средства для создания крупномасштабных сред, разработки датчиков с множеством уровней точности, а также позволяет проводить тестирование на основе сценариев использования. Процедурная генерация сред производится с помощью уникального конвейера, гибкого в отношении географических областей, приложений систем беспилотной езды и источников данных.
НПП ИТЭЛМА всегда рада молодым специалистам, выпускникам автомобильных, технических вузов, а также физико-математических факультетов любых других высших учебных заведений.
У вас будет возможность разрабатывать софт разного уровня, тестировать, запускать в производство и видеть в действии готовые автомобильные изделия, к созданию которых вы приложили руку.
В компании организован специальный испытательный центр, дающий возможность проводить исследования в области управления ДВС, в том числе и в составе автомобиля. Испытательная лаборатория включает моторные боксы, барабанные стенды, температурную и климатическую установки, вибрационный стенд, камеру соляного тумана, рентгеновскую установку и другое специализированное оборудование.
Если вам интересно попробовать свои силы в решении тех задач, которые у нас есть, пишите в личку.
Мы большая компания-разработчик automotive компонентов. В компании трудится около 2500 сотрудников, в том числе 650 инженеров.
Мы, пожалуй, самый сильный в России центр компетенций по разработке автомобильной электроники. Сейчас активно растем и открыли много вакансий (порядка 30, в том числе в регионах), таких как инженер-программист, инженер-конструктор, ведущий инженер-разработчик (DSP-программист) и др.
У нас много интересных задач от автопроизводителей и концернов, двигающих индустрию. Если хотите расти, как специалист, и учиться у лучших, будем рады видеть вас в нашей команде. Также мы готовы делиться экспертизой, самым важным что происходит в automotive. Задавайте нам любые вопросы, ответим, пообсуждаем.
Алгоритмы построения пути для беспилотного автомобиля. Лекция Яндекса
Яндекс уже некоторое время ведет разработку беспилотного автомобиля. Перед вами одна из первых технических лекций на эту тему. В направлении беспилотных автомобилей работают сотрудники Яндекса в разных городах, включая и Минск. Автор лекции Роман Удовиченко как раз из Минска — он руководит группой обработки дорожной ситуации. На сентябрьском Я.Субботнике Роман рассказал об одной из больших задач, стоящих перед его группой.
Мы просто берем текущее положение машины, смотрим на путь, по которому мы хотели бы ехать, и плавно сворачиваем на этот путь, выруливаем на него. Получается достаточно просто. Но перемещение в городе связано с тем, что нужно соблюдать правила дорожного движения.
— Меня зовут Рома Удовиченко, я работаю в Яндексе в Минске руководителем группы обработки дорожной ситуации в направлении беспилотных автомобилей. Сегодня расскажу про очень небольшую, но важную часть нашей работы — алгоритмах построения пути для беспилотного автомобиля.
Сначала хочется понять, что нужно сделать, чтобы научить машину ездить самостоятельно — при условии, что мы обвешали ее датчиками, навесили на нее камер, радаров и чего угодно. Мы можем делать всё, осталось написать код предположений.
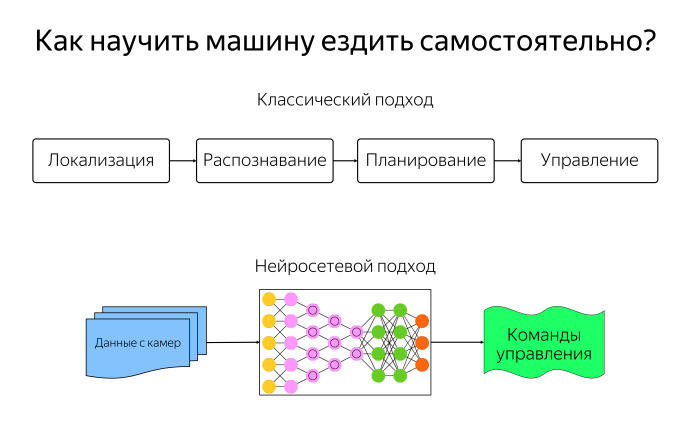
Мы можем использовать классический подход из робототехники. Разобьем нашу задачу самостоятельного передвижения на четыре модуля. Модуль локализации отвечает за то, чтобы машина понимала, где она находится. Модуль распознавания — за то, что находится вокруг машины. Модуль планирования обладает информацией о том, что находится вокруг, и зная, куда хочется приехать, строит маршрут. Модуль управления говорит, как же ехать по маршруту, чтобы приехать, выполнить эту траекторию.
А можем применить модную нынче технологию нейросетей и сказать, что в явном виде мы программировать ничего не будем. Давайте просто картинку с камер подавать в нейросеть, предварительно ее обучив на каких-нибудь человеческих перемещениях. Обучим, в каких ситуациях куда нужно крутить руль, тормозить, газовать, возьмем много-много данных, сделаем большую нейросеть, и по задумке она должна хорошо себя вести после этого.
В этом направлении ведутся большие работы, но на практике кажется, что нужно все-таки слишком много данных, нужна слишком большая нейросеть, чтобы за человеком все успешно повторять в различных ситуациях. Поэтому сегодня мы поговорим о классическом подходе, в частности — о планировании пути, построении траектории, по которой мы будем ехать.
Почему планирование пути — сложная задача, которую нельзя сделать за неделю и дальше пойти делать что-то интересное? Автомобиль вообще обладает рядом довольно существенных ограничений. Это не шар в пространстве, который может катиться в любую сторону и условно мгновенно останавливаться и замедляться. У автомобиля есть текущее направление, угол поворота колес, и он не может просто оказаться на два метра левее от текущего местоположения, это очень сложно. Он может ехать примерно вперед, поворачивая на какой-то угол, но тем не менее, перемещение очень сильно ограничено. И траектория, которую мы строим, подвержена ограничениям, которые следуют из кинематики. Например, мы не можем мгновенно разогнаться и даже мгновенно увеличить свое ускорение.
Сегодня мы рассмотрим такие разновидности алгоритмов построения пути, по которым машина может ехать хорошо. В частности, более-менее классические алгоритмы на графах, оптимизационные методы, использующие непрерывные математические оптимизации, стохастические алгоритмы, которые рассматривают случайное поведение, и специализированные методы, которые решают очень частную задачу, но решают ее очень хорошо — лучше, чем в общем случае.
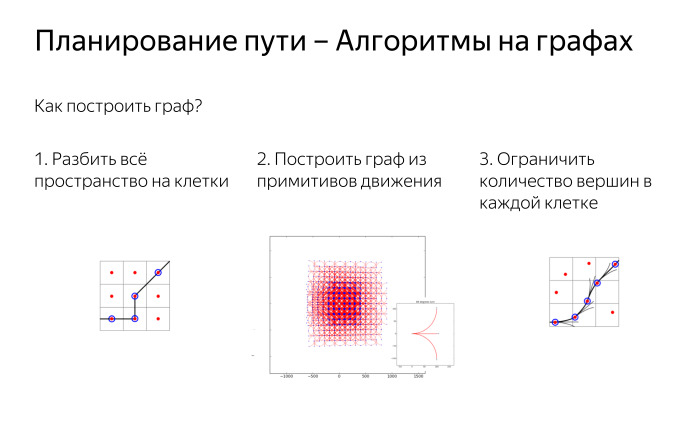
Первое, с чего начнем, это алгоритмы на графах. Первый вопрос, на который нам необходимо ответить, чтобы понять, какие алгоритмы можно применить, это как вообще построить граф? Вот стоит машина, мы можем понять, где она стоит, но в реальности графа никакого нет, вершин ребер на дороге не нарисовано. Нам этот граф нужно как-то придумать самим. Первое, что можем сделать: разобьем все пространство на клетки, рассмотрим маленькие клеточки и скажем, что есть вся наша поверхность земли, разбитая на клетки 25 на 25 или 50 на 50 см. Потом соединим соседние клетки ребрами и будем искать на них путь. Это будет довольно далеко от того пути, который машина может проехать, но какое-то приближение это даст. И у нас будут такие вершины в двумерном пространстве.
Мы можем усложнять наше пространство, добавляя туда текущий угол поворота машины. У нас уже будут клетки не просто x и y, но и текущая ориентация машины в направлениях север, юг, запад и восток, тоже как-то дискретизированных. Кроме направления мы можем много всего учитывать: текущую скорость машины, текущее ускорение, текущее тангенциальное ускорение, нормальное. Все это важно учитывать. Но чем больше мы усложняем наше пространство, тем более сложным становится наш граф.
Помимо разбиения пространства на клеточки, мы можем сказать, что способны двигаться небольшими шагами в виде примитивов. Например — проехать 50 см вперед или проехать 50 см вперед и повернуть налево или проехать 50 см вперед и повернуть направо. И такими примитивами мы можем замостить все наше пространство. В явном виде клеточек у нас нет, но если эти мелкие шаги достаточно хорошо согласованы друг с другом, то у нас получается регулярная сетка, которая хорошо и аккуратненько покрывает пространство.
Предположим, мы рассмотрим не столь хорошо стыкующиеся друг с другом примитивы — например, скажем, что поворот налево происходит под углом 89 градусов, а поворот направо под углом 90 градусов. Тогда у нас уже такое же количество вершин, как на предыдущей картинке, будет занимать существенно меньшую площадь пространства, поскольку они плохо друг с другом стыкуются и плотность точек будет очень высокая, а покрыть пространство далеко мы не сможем.
Можем объединить эти два подхода и сказать, что мы рассматриваем примитивы движения под любыми углами, проехать вперед, проехать вперед и повернуть на 10 градусов, 15 градусов, что угодно. При этом все равно разобьем пространство на клеточки и скажем, что в одной клетке не может быть больше 1, 2, …, k вершин.
Когда мы рассматриваем очередную вершину в графе в процессе использования какого-то алгоритма, мы говорим, что тут в клетке новая вершина, обрабатываем ее соответствующим образом. Если потом оказывается, что мы в указанную клетку хотим попасть уже в другой вершине, то мы ее рассматривать не будем. Это нас лишает возможности построить какой-то более оптимальный маршрут, чем если бы мы использовали все-все вершины. Зато это позволяет существенно повысить скорость работы и эффективность.
У нас есть граф, мы хотим на нем применить какой-то алгоритм. Есть алгоритм А*.
Есть алгоритм Дейкстры, который чуть более известен, чем алгоритм А*, и который обходит все вершины в графе по возрастанию расстояния от стартовой вершины. Достает их из какой-то очереди с приоритетом в порядке увеличения расстояния. На верхнем рисунке мы видим, что если стартовая розовая вершина находится в начале, то мы постепенно рассмотрим все вершины на радиусе, возрастающем от стартовой, и в итоге придем в вершину, которая является нашей целью.
Чтобы производить поиск более эффективно, мы будем рассматривать вершины не только по увеличению расстояния от старта, а еще и прибавим к этому расстоянию некоторую эвристическую оценку того, сколько нам осталось ехать до конца. Логика очень понятна: мы не просто говорим, что мы сейчас стоим в какой-то вершине и поэтому рассматриваем следующую по очереди вершину на каком-то удалении от старта. Мы еще к этому параметру добавляем какую-то функцию, позволяющую нам оценить более перспективные вершины, от которых, скорее всего, до финиша ехать недалеко. Мы не знаем, сколько на самом деле ехать от каждой вершины до финиша, потому что если бы мы знали, нам и путь не надо было бы искать. Но мы можем это как-то оценить и получить картинку на нижнем рисунке. Мы будем оценивать вершины, которые как-то идут в сторону нашей цели, и рассмотрим существенно меньшее количество вершин, чем в алгоритме Дейкстры. Про это можно много рассказывать, но в целом идея в том, что для корректной работы алгоритма необходимо, чтобы наша эвристика, функция оценки расстояния до конечной вершины, никогда не превышала настоящего расстояния, которое нам осталось проехать. Только в этом случае гарантируется правильная работа алгоритма.
В качестве эвристических функций можно использовать разные подходы. В этом и заключается сложность применения алгоритма А*. Чем более качественные эвристики вы сможете подобрать, тем лучше он будет идти в сторону цели, тем меньше вершин он рассмотрит и тем быстрее он будет работать.
Самое простое, что мы можем сделать, это рассмотреть расстояние до цели напрямик. Очевидно, мы не можем приехать к конечной точке быстрее, чем если мы просто как танк поедем к ней напрямик.
Более сложная и более эффективная эвристика — расстояние с учетом наших кинематических ограничений, но без учета препятствий. Предположим, в мире ничего нет, только мы и цель, но машина не может мгновенно перемещаться влево или вправо, ездит по своим законам, по имеющейся физической модели машины. Поскольку никаких препятствий нет, мы можем заранее просчитать расстояние до цели из различных мест, в которых мы можем находиться, и использовать это в качестве эвристической функции.
Можем поступить наоборот: сказать, что препятствие есть, но, допустим, машина умеет двигаться вперед, назад, влево, вправо, как угодно, быстро разгоняться и быстро тормозить. Построим наше расстояние с учетом препятствий, которые мы видим. Снова получится оценка, находящаяся ниже, чем реальное расстояние, которое нам осталось проехать.
И наконец, из всех эвристик мы можем рассмотреть максимум. Поскольку каждая из них не превышает нашего действительного расстояния, максимум из них тоже не будет превышать действительного расстояния и алгоритм будет работать неплохо.
Что мы получаем? Алгоритм А* позволяет найти заведомо оптимальный путь, который ведет нас к цели, огибая препятствия. Но если у нас пространство малой размерности, мы учитываем только x, y, ориентацию машины и то, что она не может мгновенно разогнаться, — значит, все эти ограничения будут учтены. Если мы будем в наш граф добавлять большое количество параметров, то он будет находиться в пространстве очень высокой размерности. У нас будет 7-, 8-, 10-мерное пространство, мы будем успевать рассматривать небольшие кусочки этого пространства и не сможем построить достаточно далекий маршрут из-за очень высокой вариативность параметров. В каких-то ситуациях А* сложно применять, а где-то он достаточно неплохо себя показывает.
Второй вариант — оптимизационные методы, основанные не на дискретном, а на более непрерывном подходе.

Постановка задачи может быть такой: рассмотрим траекторию нашего положения во времени, x и y, зависящие от времени t, то есть поймем, в какой точке мы хотим оказаться в момент времени t. Мы можем определить угол касательной через арктангенс от производных, можем сказать, что оптимальной в этом случае будет траектория, которая минимизирует функционал, являющийся интегралом по времени вперед от какой-то функции от траектории. Функция от траектории здесь каким-либо образом нас штрафует за резкие повороты, резкие разгоны, нахождение близко к препятствиям и т. д. Тогда, если мы просуммируем вдоль нашей траектории все эти штрафы, которые мы сами себе придумаем, и попытаемся это минимизировать стандартным математическим аппаратом, никак не связанным с автомобилями в целом и беспилотными автомобилями в частности, то мы решим задачу в каком-то общем виде.
Какие мы можем рассмотреть примеры штрафов? Например, можем сказать, что мы не хотим подъезжать близко к препятствиям, учитывать это с каким-то весом, не хотим, чтобы наша скорость была гораздо выше или ниже желаемой скорости, которую мы для себя определили. Мы можем штрафовать себя за вторую производную, которая является ускорением, потому что мы не хотим, чтобы машина резко топила в пол и резко тормозила.
Можем рассмотреть третью производную, которая является рывком, то есть мы не хотим, чтобы ускорение тоже менялось достаточно резко. Кстати, именно от резкого изменения ускорения людей укачивает в процессе езды. Если ускорение фиксированное и машина просто все время разгоняется, то, как показывают исследования, людей не укачивает. Вестибулярный аппарат человека улавливает и не всегда хорошо реагирует, если она то разгоняется, то тормозит. Мы можем не хотеть делать крутые повороты, ограничиваем наш угол. И есть дополнительные ограничения, которые говорят, что машина физически не может разгоняться быстрее какого-то ускорения. Если все мы это учтем каким-то образом, то сможем решить задачу с помощью абстрактного алгоритма минимизации функции и получим некий результат.
Отдельно хочется поговорить про вычисления расстояний, потому что в большинстве методов оптимизации очень любят работать с плавными функциями, которые хорошо дифференцируемые, гладенькие. Тогда там все работает хорошо. А наша машина — объект довольно сложной формы, и препятствия, которые мы объезжаем, это тоже объекты хитрых форм. Поэтому тут нужно производить какое-то упрощение. Например, мы можем сказать, что машина — не что-то сложное, а просто пять окружностей, которые ездят туда-сюда.
Это будет похоже на правду, хоть и не до конца, но приближение хорошее. А от окружностей очень легко считать расстояния до чего угодно и очень легко проверять окружность на пересечения с остальными геометрическими примитивами. Если расстояние до центра меньше, чем радиус, то вот пересечение, иначе все хорошо.
Что нужно, чтобы плавно изменялось расстояние? Наше эвклидово расстояние до невыпуклых многоугольников не обладает необходимыми нам свойствами и плохо дифференцируемо в местах, где эта невыпуклость возникает. Поэтому мы можем построить такое псевдорасстояние по градиентному полю до нашей ломаной, она здесь обозначена красным и представляет собой препятствие. Мы можем довольно несложно ввести поле расстояний от каждой точки до этой ломаной, которая направлена в сторону ломаной и обладает необходимыми свойствами дифференцируемости — пусть и не являясь строго кратчайшей. Если мы все это сделаем — сможем построить гладкую, красивую и аккуратную траекторию.
К преимуществам таких методов мы относим то, что получается хорошая траектория и пространство управления непрерывно. Мы можем по нему ехать, все ограничения в той или иной степени соблюдаются. Но к сожалению, большинство оптимизационных методов или даже почти все так или иначе страдают от локальных минимумов, где их попытки что-либо оптимизировать застревают и не находят достаточно хорошего решения. Очень сложно все формулировать в виде математических дифференцируемых функций, это тоже не всегда получается.
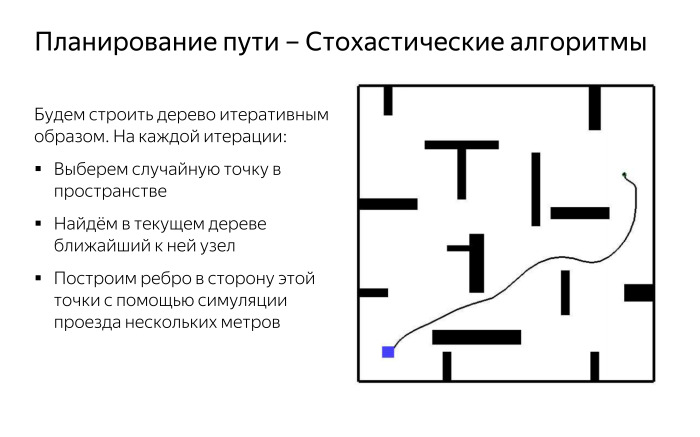
Однако выход есть. Мы можем применить алгоритмы, которые работают некоторым случайным образом, но зато позволяют нам построить какой-то приближенный маршрут достаточно быстро и удобно. Например, мы будем строить наш граф, являющийся деревом, итеративным образом. Вначале ничего делить на клеточки не будем, никаких примитивов строить не будем. Мы просто возьмем симулятор нашей машины, который в целом умеет симулировать движение, максимально похожее на то, как машина едет по-настоящему. И возьмем стартовую точку. После этого итеративно выберем случайную точку в пространстве. И — найдем в текущем построенном дереве ближайший к ней узел. Построим ребро в сторону этой точки с помощью симуляции проезда в эту сторону.
Получается, мы каждый раз едем от нашего построенного дерева в случайную сторону и можем вершины в этом дереве делать в пространстве любой размерности, то есть в каждой вершине учитывать текущее направление машины, текущую скорость, ускорение, все углы, которые нам важны. А потом, когда мы возьмем новую точку, то возьмем и ближайшую к этой точке вершину. Проедем с помощью какой-то симуляции, например, 5 метров в сторону этой точки. Затем возьмем другую точку и проедем в ее сторону.
Что нам это дает? Мы каждый раз исследуем пространство, но очень агрессивно. Мы не ищем оптимальные способы объехать препятствие. Мы просто ездим в разные стороны, но каждый раз делаем это из наиболее исследуемого участка нашего пространства к той, неизведанной стороне.

За счет этого мы довольно быстро получаем картину, где в разные стороны растут «щупальца», которые как-то покрывают наше пространство. Возможно, неоптимально, но довольно быстро. Квадратик в углу — наша стартовая позиция. Потом мы можем получить какой-то путь к цели, который выглядит, возможно, не совсем оптимально и элегантно, но зато получен достаточно быстрым способом.
И получается, преимущества заключаются в том, что мы работаем очень быстро в многомерных пространствах. Поскольку мы пути получаем с помощью честной симуляции, то практически напрямую можем передавать их в управляющий блок. Недостатки? У нас нет гарантий, что наши точки будут выбираться достаточно хорошо. Решения могут получаться довольно кривые и не всегда оптимальные.
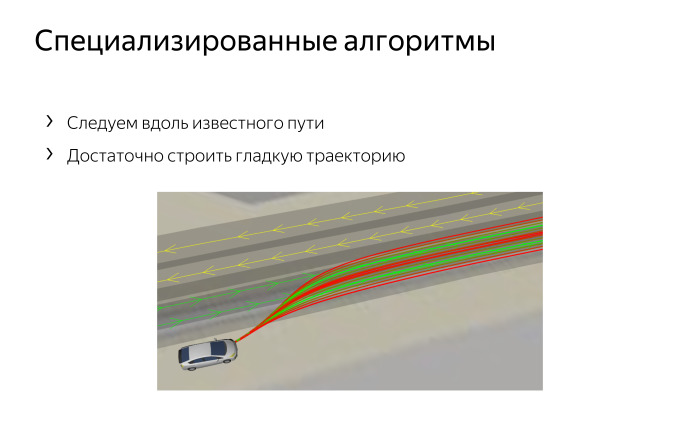
Специализированные методы. Когда машина ездит в городе, у нас нет абстрактных точек А и Б и неструктурированного окружения со случайными препятствиями. У нас в городе все более-менее понятно: есть конкретные полосы и движение нашей машины почти всегда заключается в том, что мы едем примерно по центру полосы, иногда смещаемся левее или правее, чтобы объехать препятствие, иногда перестраиваемся, чтобы по правилам дорожного движения повернуть туда, куда нужно. На перекрестках из одной полосы в другую перестраиваемся.

Нам не всегда нужны эти хитрые деревья, чтобы парковаться или делать сложные маневры. Они нужны, но когда мы едем на полосе, нам достаточно построить более-менее плавную траекторию, следующую к центру этой полосы или с каким-то смещением влево-вправо. Это сделать гораздо проще, чем искать абстрактный путь в графе. Мы просто берем текущее положение машины, смотрим на путь, по которому мы хотели бы ехать, и плавно сворачиваем на этот путь, выруливаем на него. Получается достаточно просто. Но перемещение в городе связано с тем, что нужно соблюдать правила дорожного движения.
Это не совсем связано с правилами построения пути, но от них недалеко. Когда мы подъезжаем к перекрестку, нам нужно остановиться, пропустить двигающиеся там машины. Мы не можем рандомно ездить, можем по одной ехать или по другой, перестраиваться, должны останавливаться на красный свет светофора, пропускать пешеходов и т. д. И нам нужно соблюдать правила дорожного движения, информацию о которых машина может получать либо заранее из какой-то очень подробной карты, либо распознавать на ходу по разметке, знакам и т. д.
И с тем, чтобы распознавать все это на ходу, есть некоторая проблема. Беспилотный автомобиль довольно легко поместить в ловушку.
Из нее он, следуя правилам, не сможет выбраться. Это шутка о том, что в жизни случается много ситуаций, в которых человек понимает, что делать. Здесь сплошная полоса, а впереди ремонт дороги. Рабочие не поставили все нужные знаки про объезд. Они просто поставили свой цементовоз, ломают асфальт. Человек поймет, что от пересечения сплошной линии ничего страшного не случится — его, наверное, даже не оштрафуют. А вот с беспилотными автомобилями все сложнее.
В целом в процессе решения возникает очень много задач построения пути — во всех смежных областях, которые были сначала. Если вы хотите помочь нам разбираться с этими сложностями и реализовывать всё в алгоритмах — обязательно приходите к нам наносить добро. Мы будем рады вас видеть в минской группе разработки. Построение различных путей, учет правил дорожного движения — как раз одна из наших тем. Большое спасибо.